$CSP2019$算法总结---$DP$
区间\(DP\)题目清单:
状态设计
\(1.\)对于这一类问题,一般设计状态为\(dp[i][j]\),表示完成\(i-j\)区间的答案。
\(2.\)有一些奇葩的情况,可以这样设计状态:\(dp[i][j]\)表示完成\(j\)时,左端点为\(i\),右端点为\(j-1\)
状态转移
思想是用已经更新的小区间扩展到未被更新的大区间,关键在于如何更新,如何扩展
一种办法是枚举断点把一个大区间划分成小区间
另一种办法是奇葩的倍增思想传送门
有三种\(DP\)顺序
\(1.\)先枚举区间长度,再枚举左端点,再枚举断点,因为区间长度从小到大,所以子状态一定都被更新,切忌先枚举左端点。
\(2.\)倒序枚举,即左端点(\(i\))\(n->1\),右端点(\(j\))\(i->n\),断点\(i-->j\)。
\(3.\)记忆化搜索,这样做无需考虑枚举顺序
\(4.\)倍增思想,\(dp[i-1][dp[i-1][j]]\),见上面链接
需要注意几点:
\(1.\)注意初始化区间长度为\(1\)时的\(DP\)值,求最小值还需要初始化所有区间为最大值
\(2.\)对于环应该先将它断开变成两倍长的链再区间\(DP\),最后对于所有\(dp[i][i+n]\)取答案
\(3.\)有时候最优答案不一定会出现在\(dp[1][n]\),需要对于\(DP\)过程中每一个值取最优值。
\(DP\)优化
一、四边形不等式
使用范围:区间序列\(DP\)求最小值(一定是最小值)
对于动态规划转移方程
dp[i][j]=min(dp[i][k],dp[k+1][j])+w(i,j);
其中\(w(i,j)\)只受\(i,j\)取值影响
如果满足下面两个条件
\(1.\)区间单调性:如果对于\(\forall i \leq i'< j' \leq j,w(i',j') \leq w(i,j)\)(即小区间取值\(\leq\)大区间取值)
\(2.\)四边形不等式:\(\forall i \leq i'< j' \leq j,w(i,j)+w(i',j')\leq w(i',j)+w(i,j')\)
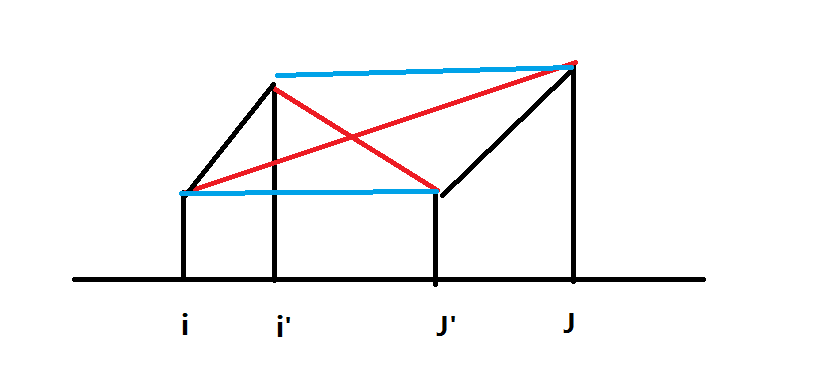
即中的红线总长\(\geq\) 蓝线总长
如果\(w(i,j)\)同时满足区间单调性和四边形不等式,那么\(f(i,j)\)满足四边形不等式
令\(S(i,j)\)为\(F(i,j)\)在取到最优解时的决策点\(k\)
那么决策本身具有单调性,即满足\(S(i,j)\leq S(i,j+1)\leq S(i+1,j+1)\)
用\(j\)代替\(j+1\)得到
\(S(i,j-1)\leq S(i,j)\leq S(i,j+1)\)
转移方程变为
\(F(i,j)=min(F(i,k)+F(k+1,j))+w(i,j);\ (S(i,j-1)\leq k\leq S(i+1,j))\)
可以证明,他将时间复杂度降到了\(O(n^2)\)
什么时候使用四边形不等式?
只需要牢记公式
\(S(i,j-1)\leq S(i,j)\leq S(i,j+1)\)
考试时可以打一张决策表看是否满足上面式子,满足可以使用四边形不等式
\(1.\)序列\(DP\)有时可以使用四边形不等式优化,但仅仅是常数优化
\(2.\)需要注意四边形不等式仅针对求最小值的情况
\(3.\)注意\(S\)数组(下标取值范围)需要初始化,\(S[i][i]=i\)
树形\(DP\)
题目清单:
状态设计
对于这一类\(DP\),一般设计两维状态,\(DP[i][j]\)表示当前节点为\(i\),子节点或相邻节点的状态为\(j\)时的答案
状态转移
\(1.\)树形结构天然的\(dfs\)序保证了更新当前节点时子节点已经被更新完毕,所以就把\(DP\)过程放到\(dfs\)遍历中即可,注意初始化。
一般每搜索一颗子树回溯回来就更新答案,最后在循环外面向上回溯前自己更新自己答案
\(2.\)当然还有种状态转移是需要所有相邻节点的状态,对于这种问题直接\(for\)循环枚举所有点即可,但要注意枚举顺序,是否会出现状态没有的情况,用多维循环内层枚举当前点,最内层枚举相邻点
状压\(DP\)
题目清单

状态设计
状压\(DP\)是一类非常特殊的\(DP\),基本思想是把\(DP\)的状态压缩为二进制等,以减小空间且保证转移正确性
一般看到一个题数据范围是\(n<=18\)且是动态规划,则大概率是状压\(DP\)
状态设计时,一维用二进制记录状态,一般在\((1<<n)-1\)左右,如果需要可以设计另一维表示当前位置,对于很多与选择顺序无关的题目这一维可以省略。
也有时候第二维可以分割为另一个\(DP\)数组,大大优化空间
状态转移
\(1.\)位运算的使用:位运算可以提高效率且减少代码复杂度
s<<=1 //左移*2
s>>=1 //右移/2
(s&(1<<i-1)) //判断第i位是不是1
s|=(1<<i-1) //把第i位设置成1
s&=~(1<<i-1) //把第i位设置成0
s^=(1<<i-1) //把第i位取反
s&=s-1 //把s最靠右的1去掉
s&(-s) //返回最靠右的1代表的值
for(s0=s;s0;s0=(s0-1)&s) //依次枚举s的子集
(1<<n)-1 //n位全是1的状态
(s&((1<<n)-1)) //只保留s的前n位,避免越界
\(2.\)状压\(DP\)转移
重点在于考虑记录哪些状态
一般一维枚举前一个状态(一般是最外层),另一维枚举转移什么(一般是一个值);少数情况第二维枚举接下来状态,因为这样复杂度极大,一般需要剪枝;极少数情况很毒瘤,表面上看起来只能枚举两种状态,但可以拆到另外一个\(DP\)数组,变为第一种转移方式,比如装箱问题,要求数量最小,可以用一个\(DP\)记录最后一个箱子剩余空间,从而\(O(Sn)\)转移,不过要注意辅助\(DP\)数组被更新的前提是正常\(DP\)数组能被更新,是一个依赖关系,也就是在保证第一答案最优时第二答案最优,这样是对的
传送门
\(3.\)优化问题
\((1)\)很多无用状态可以不枚举,比如炮兵阵地问题,可以预处理每一行的合法情况装进\(vector\),\(DP\)时只需要枚举这些情况,大大降低复杂度。
\((2)\)还有一类问题:愤怒的小鸟,在所有已有状态中枚举找到一个值,再枚举不在状态中的值,复杂度是\(O(n^2)\),但最优解与选择顺序无关,所以可以控制每次选择最小位置更新,复杂度\(O(n)\)
\((3)\)对于区间、字符串操作,可以压缩状态后连边,跑最短路求解
\((4)\)与考虑顺序无关的\(DP\)可以优化掉一维,只与附近固定位置有关,可以使用滚动数组优化
一定要小心MLE!!!!!
数位\(DP\)
状态设计
一般数据范围为\(10^{18}\)
通常使用多维,每维规模比较小。
如\(dp[i][j][k][0/1]\)表示当前在第\(i\)位(从最低位到最高位编号),当前位置是\(j\),附近位置的状态是\(k\),是否满足题目要求条件时的方案数(一般记忆化搜索\(k\)表示前面状态,递推\(dp\ k\)表示后面状态,记忆化搜索还需要记录是否小于边界)
状态转移
数位\(DP\)一般有两种做法:\(1.\)递推计数,\(2.\)记忆化搜索,两者的核心思想:逼近法,逐位确定是一样的
逼近法(先讨论\(1-x\)的答案)
分两种情况讨论,一种是位数\(<cnt\),一种是和答案位数相同,一般不考虑前导零,第一种情况需要单独处理
对于第一种情况,位数小于边界位数,枚举的数一定小于边界,枚举位数是多少,第一位\(\in [1,9]\),后面位置随便取数即可,直接计数。
对于第二种情况,逐位确定,首先最高位\(\in [1,a[cnt])\)时一定是小于边界的,所以后面位置随便取,计数,然后确定最高位为\(a[cnt]\),处理下一位,最终逼近到边界(需要注意的是最后会停在\(x-1\),可以单独处理\(x\),或者提前把边界\(+1\))。每次都不卡到边界上,保证后面所有位置可以随意取值便于计数
下面以\(65536\)为例看一下如何逼近(\(x\)表示该位置可以随意取数)

如果题目要求\([L,R]\)的答案,直接求\(ans[L-1],ans[R]\),作差即可。
继续回到状态转移上
对于递推计数的方法,首先要预处理\(dp\)数组(本身是数位\(DP\)),再按照逼近法计数,状态多的时候预处理会很麻烦,需要边界\(+1\)
对于记忆化搜索,只需要边搜索边记录\(DP\)数组即可,对于这种方法,状态转移比较简单,码量小,比较容易思考,边界不需要提前\(+1\)
注意的问题
\(1.\)递推计数预处理时有时可以用前缀和等等方法优化
\(2.\)初始值为\(-1\)时,小心数组下标越界
\(3.\)看好题目范围中是否包含\(0\)
\(4.\)前导零情况单独处理



