【学习笔记】manacher算法
\(manacher\)算法解决的问题是求一个字符串中的最长回文字串，也就是极长回文子串的长度，长度大约在\(10^7\)
引入
回文串有两种情况：长度为奇数和长度为偶数
若长度为奇数则对称轴落在中间字符上，若长度为偶数则对称轴落在中间两个字符之间
如果这两种情况都考虑就会复杂很多，我们可以在每两个字符之间（包括开头结尾）加入一个分隔符
比如\(abcdefg\)变成\(|a|b|c|d|e|f|g|\)
这样对称轴一定在字符上，若\(x\)表示一个对称轴向外扩展长度，那么答案就是\(x-1\)，一会给出证明
先说朴素做法：
\(1.O(n^3)枚举左右端点，再扫描\)
\(2.枚举对称轴所在字符，左右同时扩展,O(n^2)\)
这道题要求\(O(n)\)复杂度的做法
\(Manacher\)
\(manacher\)算法实际上是上面的第二种算法改进而来的，考虑下面这种情况
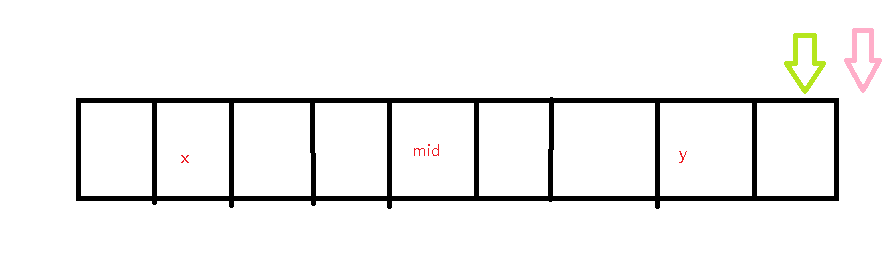
假设从\(mid\)处扩展，能最远扩展到绿箭头上（最右点是时刻更新的），记为\(r\)，那么\(r\)右边的情况是未知的，假设我们现在最外层枚举到了\(y\)点，注意到\(y\)和\(x\)是关于\(mid\)对称的，那么以\(x\)为对称轴的回文串有可能左边界超出\(l\)，也有可能没有超出，根据回文串的性质，\(y\)能扩展的长度一定大于等于 \(x\)回文串能扩展的长度和到右边界距离的最小值（因为边界右边的情况是不知道的）。
所以我们可以赋值\(y\)的初始值，这样\(y\)的长度可以不从\(0\)开始扩展，优化了程序。
可以证明这个算法时间复杂度为\(O(n)\)
至于输出长度的问题，我们记录的是向外扩展的最大距离，注意包括对称轴。对于\(a|b|c|d|e\)
有下面两种情况：
\(1.\)对称轴在分隔符上，这时候长度为一边的字母数\(*2+1\)，因为开头结尾也加了分隔符，扩展一定最远一定在分隔符上，扩展到一边的字母数也就是\((len-1)/2\)，两边总的长度是\(len-1\)
\(2.\)对称轴在字母上，这时长度为一边的字母数\(*2\)，扩展到一边的字母数是\(len/2\)，再乘\(2\)发现中间字母多算一遍，所以长度也是\(len-1\)
注意一下几点
\(1.\)初始扩展距离赋成\(1\)
\(2.\)开头结尾的两边再加不同的字符，避免数组越界
比如\(*|a|b|c|d|e|f||\)
更多非常巧妙的细节看代码
\(Code\)
#include<cstring>
#include<cmath>
#include<iostream>
#define maxn 30001000
using namespace std;
int n,hw[maxn],ans;
char a[maxn],s[maxn<<1];//数组一定开到两倍以上，两倍不够
void manacher()
{
int maxright=0,mid;
for(int i=1;i<n;++i)
{
if(i<maxright)//如果在已知范围内
hw[i]=min(hw[(mid<<1)-i],hw[mid]+mid-i);//mid<<1-i是中点公式，返回对称点位置，hw[mid]+mid-i=maxright-i+1
//两种情况
else
hw[i]=1;//未知则只能初始值为1
for(;s[i+hw[i]]==s[i-hw[i]];++hw[i])//这里比较巧妙，hw一开始就是1，相当于看下一个符不符合，i+hw[i]就是当前的边界+1,当不符合后最右边为i+hw[i]-1，这时候hw[i]就是扩展长度
if(hw[i]+i>maxright)
{
maxright=hw[i]+i;
mid=i;//两个都更新
}
}
}
void change()
{
s[0]=s[1]='#';//开头之前的字符是#,结尾之后无字符，数组不会越界
for(int i=0;i<n;++i)
{
s[i*2+2]=a[i];
s[i*2+3]='#';
}
n=n*2+2;//结尾后面
s[n]=0;//就是没有字符
}
int main()
{
scanf("%s",a);
n=strlen(a);
change();
manacher();
ans=1;//最短一定是1，赋初始值
for(int i=0;i<n;++i)
ans=max(ans,hw[i]);
printf("%d",ans-1);//为什么是-1推过了
}
\(Update:10.28\)
下面是解释答案为什么是\(hw-1\)的新版本，更容易理解一些
设原字符串总长度为\(len\)
假设长度为奇数，那么这个字符串是长成这样的
\(*a*a*a*a*a*\)
\(\therefore \lceil\frac{len}{2} \rceil*2=hw\)
\(\therefore \frac{len+1}{2} *2=hw\)
\(\therefore len=hw-1\)
假设长度为偶数，那么这个字符串是长成这个样子的
\(*a*a*a*a*\)
\(\therefore \frac{len}{2}*2+1=hw\)
\(\therefore len=hw-1\)
证毕
\(manacher\)求回文串个数
\(manacher\)算法还可以求所有回文字串的个数，本质不同的回文字串指的是对称中心不同，因此以\(i\)为中心的回文字串的个数是就是原字符串向右扩展的距离
设原字符串总长度为\(len\)
假设长度为奇数，那么这个字符串是长成这样的
\(*a*a*a*a*a*\)
\(\therefore \lceil\frac{len}{2} \rceil*2=hw\)
\(\therefore \frac{len+1}{2} *2=hw\)
\(\therefore len=hw-1\)
假设长度为偶数，那么这个字符串是长成这个样子的
\(*a*a*a*a*\)
\(\therefore \frac{len}{2}*2+1=hw\)
\(\therefore len=hw-1\)
证毕
假设以\(i\)为对称轴的最长回文串长度为奇数，因为一个字符也是回文串，所以以\(i\)为对称轴的回文串个数为\(\lceil \frac{len}{2}\rceil\)就是\(\frac{len+1}{2}=\frac{hw}{2}\)
假设以\(i\)为对称轴的最长回文串长度为偶数，则个数为\(\frac{len}{2}=\frac{hw-1}{2}\)
又因为\(hw\)是奇数，所以\(\frac{len}{2}=\frac{hw}{2}\)
综上，统计回文串个数只需要最后扫描加这样一句话就行
for(int i=0;i<n;++i)
ans+=hw[i]/2;
