主席树(可持久化线段树)

经典问题：求全局第K大

思路：可以在权值线段树上二分，当左儿子存储的个数大于k时在左儿子寻找，否则将k减去左儿子存储的个数在右儿子寻找

主席树经典题：求区间第k大

如果我们像全局第K大一样给每个区间建一个线段树是不可能的，考虑做一个前缀和，用第R个线段树减去第L-1个线段树就是[L,R]的线段树，再做全局第K大即可

但是仍然会MLE，事实上不需要每个数建一棵线段树，每次加入只需要插入的路径上更新即可，所以每次的空间复杂度是O(logn)

这样做实际上可以回到任何一个历史状态，这就是所谓的可持久化线段树——主席树

 

需要注意的是，因为要更新路径，我们按照遍历的顺序每到一个新节点编号加一（不同于传统线段树左儿子是P>>1右儿子是P>>1|1的编号方式）

 数组注释：lc[i]表示i的左儿子,rc[i]表示i的右儿子,rt[i]表示第i次更改时的根编号

build函数

void build(int &t,int l,int r)
{
    t=++cnt;//每访问一个新的节点就编号加一 
    if(l==r) return;
    int mid=(l+r)>>1;
    build(lc[t],l,mid);
    build(rc[t],mid+1,r);
}

比较简单，需要注意是按遍历顺序开点

modify函数（insert）

int modify(int o,int l,int r)//o表示上一个状态的编号 
{
    int h=++cnt;
    lc[h]=lc[o]; rc[h]=rc[o];/*左右儿子都复制一下*/ sums[h]=sums[o]+1;//当前节点处于插入路径上，需要更新 
    if(l==r) return h;
    int mid=(l+r)>>1;
    if(place<=mid) lc[h]=modify(lc[h],l,mid);//将lc[h]更新，成链状 
    else rc[h]=modify(rc[h],mid+1,r);
    return h;
}

比较重要的函数，可以结合图片理解

以下是插入数字4时的情况

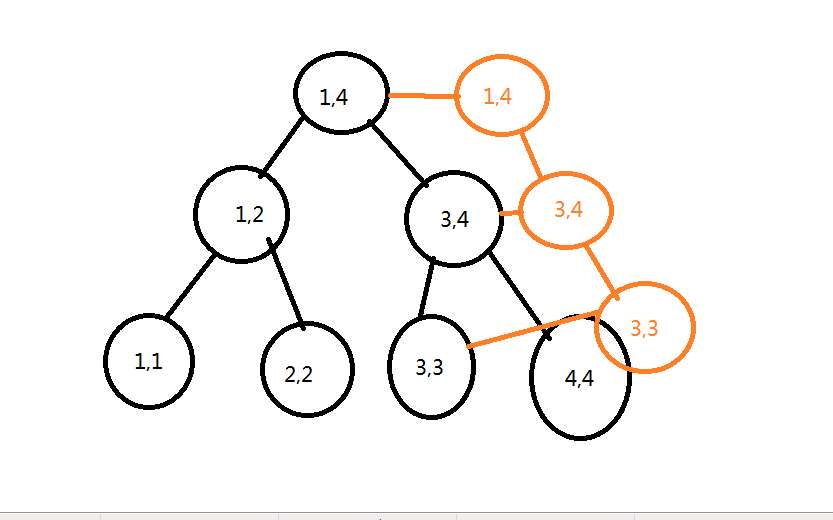
query函数

//u是l-1时的线段树，v是r时的线段树
//query(rt[l-1],rt[r],1,num,k) 
int query(int u,int v,int l,int r,int k)
{
    int ans,mid=(l+r)>>1;
    int x=sums[lc[v]]-sums[lc[u]];//相当于[l,r]线段树lc[x]所存的个数 
    if(l==r) return l;//找到了第k小 
    if(x>=k) ans=query(lc[u],lc[v],l,mid,k);
    else ans=query(rc[u],rc[v],mid+1,r,k-x);
    return ans; //别忘了return 回去 
}

前缀和的思想，前缀减前缀，区间变全局

code

#include<cstdio>
#include<iostream>
#include<algorithm> 
#define N 500005
using namespace std;
int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int a[N],index[N],rt[N],lc[N<<3],b[N];
int l,r,k,ans,num,place,n,m;
int cnt,sums[N<<3],rc[N<<3];
void build(int &t,int l,int r)
{
    t=++cnt;//每访问一个新的节点就编号加一 
    if(l==r) return;
    int mid=(l+r)>>1;
    build(lc[t],l,mid);
    build(rc[t],mid+1,r);
}
int modify(int o,int l,int r)//o表示上一个状态的编号 
{
    int h=++cnt;
    lc[h]=lc[o]; rc[h]=rc[o];/*左右儿子都复制一下*/ sums[h]=sums[o]+1;//当前节点处于插入路径上，需要更新 
    if(l==r) return h;
    int mid=(l+r)>>1;
    if(place<=mid) lc[h]=modify(lc[h],l,mid);//将lc[h]更新，成链状 
    else rc[h]=modify(rc[h],mid+1,r);
    return h;
}
//u是l-1时的线段树，v是r时的线段树
//query(rt[l-1],rt[r],1,num,k) 
int query(int u,int v,int l,int r,int k)
{
    int ans,mid=(l+r)>>1;
    int x=sums[lc[v]]-sums[lc[u]];//相当于[l,r]线段树lc[x]所存的个数 
    if(l==r) return l;//找到了第k小 
    if(x>=k) ans=query(lc[u],lc[v],l,mid,k);
    else ans=query(rc[u],rc[v],mid+1,r,k-x);
    return ans; //别忘了return 回去 
}
int main()
{
    n=read(); m=read();
    for(register int i=1;i<=n;++i){a[i]=read();b[i]=a[i];}
    sort(b+1,b+n+1);
    num=unique(b+1,b+n+1)-b-1;//离散化 
    build(rt[0],1,num);
    for(register int i=1;i<=n;i++)
    {
        place=lower_bound(b+1,b+num+1,a[i])-b;
        rt[i]=modify(rt[i-1],1,num); 
    }
    while(m--)
    {
        l=read(); r=read(); k=read();
        ans=query(rt[l-1],rt[r],1,num,k);
        printf("%d\n",b[ans]); 
    }
    return 0;
}