论文阅读2020:ReSTIR(Spatiotemporal reservoir resampling for real-time ray tracing with dynamic direct lighting)（一):主体思想

问题引入

背景

渲染是计算机图形学的最重要方向之一，是模拟场景/模型成像的过程。渲染在建筑，游戏，模拟，电影电视特效，以及医学可视化中都有广泛的应用。目前基于物理渲染Ray Tracing仍然难以达到实时，学术界和工程界持续进行渲染性能研究和探索。ReSTIR这篇英伟达2020的文章,在图形学领域重新发现Rediscover了加权蓄水池采样（Weighted Resorvior sampling）方法，带来采样性能的巨大提升，而过去加权蓄水池主要用于金融、统计等领域。本篇文章将介绍蒙特卡洛光追和蓄水池采样用于蒙特卡洛计算的基本原理。

基于蒙特卡洛的光线追踪

渲染的基本问题是求解渲染方程，求出物体在光源的照射下，出射到人眼方向的辐射亮度(Radiance，\(L_0\))。

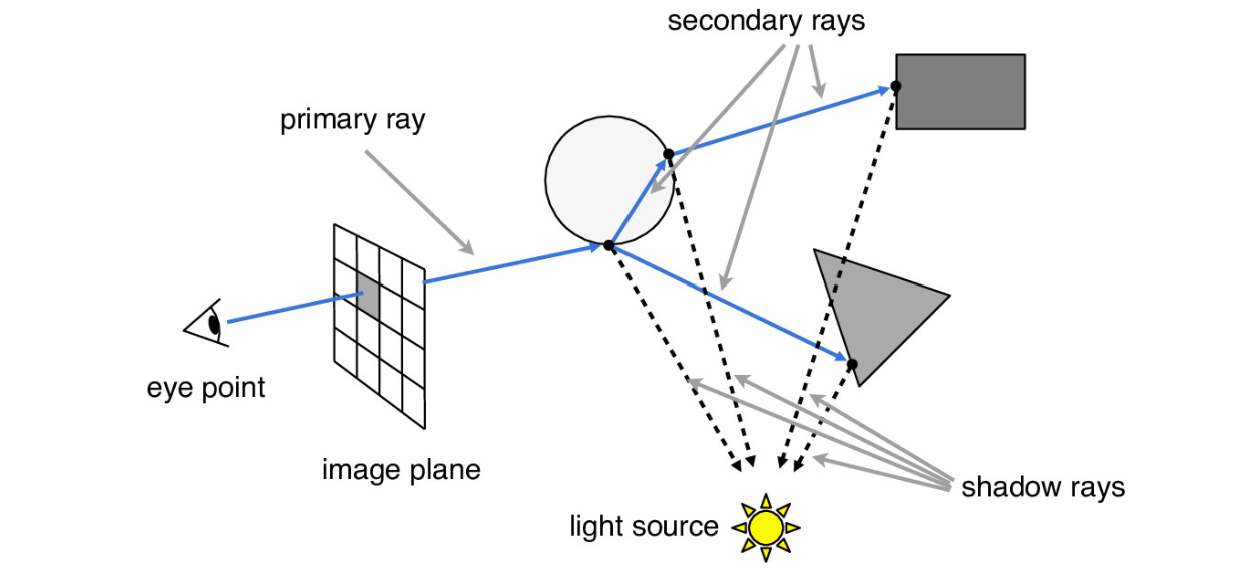
渲染方程表达如下，要计算任意一个表面位置\(x\),朝向为\(\omega_0\)的辐射亮度\(L_0(x,\omega_o)\),等于位置\(x\)处的自发光\(L_e\)，与半球面所有方向上三个乘积项乘积的积分的和，这三个乘积项分别是入射辐射亮度\(L_i\)，双向散射分布函数BRSF \(f\)，以及入射方向与表面法线的夹角的余弦值。该渲染方程展开是一个无限积分，很难求出解析解，一般采用蒙特卡洛方法进行估计。

\[L_{o}(x,\omega_o)=L_{e}\left(x, \omega_{o}\right)+\int_{\Omega} L_{i}\left(x, \omega_{o}\right) f\left(\omega_{i}, \omega_{o}\right)\langle\cos \theta\rangle d \omega_{i} \]

蒙特卡洛积分的正确性推导

• 首先我们按照概率密度函数\(p(x)\)在区间\([a,b]\)上进行采样得到样本集\(\{X_1,X_2,...,X_N\}\)
• 再构造新的\(F_N\)函数：

\[F_{N}=\frac{1}{N} \sum_{i=1}^{N} \frac{f\left(X_{i}\right)}{p\left(X_{i}\right)} \]

• 计算\(F_N\)的数学期望如下：

\[E\left[F_{N}\right]=E\left[\frac{1}{N} \sum_{i=1}^{N} \frac{f\left(X_{i}\right)}{p\left(X_{i}\right)}\right]=\frac{1}{N} \sum_{i=1}^{N} E\left[\frac{f\left(X_{i}\right)}{p\left(X_{i}\right)}\right]\\=\frac{1}{N} \sum_{i=1}^{N} \int_{a}^{b} \frac{f\left(X_{i}\right)}{p\left(X_{i}\right)} p\left(X_{i}\right) d x=\frac{1}{N} \sum_{i=1}^{N} \int_{a}^{b} f(x) d x\\=\int_{a}^{b} f(x) d x \]

• 经过上述推导以及大数定理,可以得到蒙特卡洛积分方法如下：

\[\int_{D} f(x) d x=\lim _{N \rightarrow \infty} \frac{1}{N} \sum_{i=1}^{N} \frac{f\left(X_{i}\right)}{p\left(X_{i}\right)} \]

蒙特卡洛积分法的收敛性和收敛速度分析

求上述\(F_N\)的方差如下：

\[\sigma^{2}\left(F_{N}\right)=\sigma^{2}\left[\frac{1}{N} \sum_{i=1}^{N} \frac{f\left(X_{i}\right)}{p\left(X_{i}\right)}\right]=\frac{1}{N^{2}} \sum_{i}^{N} \sigma^{2}\left[\frac{f\left(X_{i}\right)}{p\left(X_{i}\right)}\right] \]

令：

\[Y=\frac{f(X)}{p(X)} \]

则：

\[\sigma^{2}\left(F_{N}\right)=\frac{1}{N^{2}} \sum_{i}^{N} \sigma^{2}\left[Y_{i}\right]=\frac{1}{N^{2}}\left(N \sigma^{2}[Y]\right)=\frac{1}{N} \sigma^{2}[Y] \]

则：

\[\sigma\left[F_{N}\right]=\frac{1}{\sqrt{N}} \sigma[Y] \]

• 由此可知当采样个数N 趋向无穷大时, \(\sigma\left[F_{N}\right]\)趋向于0，这也证明蒙特卡洛积分法的收敛性
• 由方差公式可以知道蒙特卡洛积分法收敛速度和稳定性由\(Y\)决定，如果\(Y\)变化剧烈，就会造成方差较大，估计值的收敛速度越慢；若\(f(x)\)和\(p(x)\) 越接近(即若他们的形状越接近)，则收敛更快更稳定。最理想的情况是\(p(x) = f(x)\)或成正比，则方差为0，快速收敛。

因此，选择任意概率密度分布函数\(p(x)\)，当收敛次数足够大时，蒙特卡洛积分都会收敛；若\(f(x)\)和\(p(x)\)形状接近，成正比，则收敛更快更稳定。

利用蒙特卡洛积分计算渲染方程

利用蒙特卡洛积分计算渲染方程可写作：

\[L_{o}=L_{e}\left(x, \omega_{o}\right)+\frac{1}{N} \sum_{j=1}^{N} \frac{L_{i}\left(x, \omega_{o}\right) f\left(\omega_{i}, \omega_{o}\right)\langle\cos \theta\rangle}{p d f\left(\omega_{i}\right)} \]

当\(pdf(\omega_i)\)的分布与被积函数，即三个乘积项\(L_{i}\left(x, \omega_{o}\right) f\left(\omega_{i}, \omega_{o}\right)\langle\cos \theta\rangle\)相似时，能有效减小方差。

待解决问题

本文试图通过结合多种采样方法，例如重采样重要性采样、蓄水池采样等多种方法，达到渲染方程积分计算快速收敛，提升积分计算稳定性的目的。

方法

现有技术

重要性采样

如上述对蒙特卡洛积分收敛方差和速度的分析，尽可能选择概率密度分布函数与被积函数形状类似，或成正比时，积分收敛更快。重要性采样即一种选择特殊概率密度分布函数\(p(x)\)进行采样的策略。

RIS(Resampled Importance Sampling) 重采样重要性采样

Importance Resampling重要性重采样

假设我们对 被积函数 \(f\) 有了一个比较好的估计 \(g\)，需要生成满足分布 \(g\) 的 样本，有四种方法，分别是（1）逆变换采样（2）拒绝采样（3）Metropolis 采样（4）Importance resampling。这里主要介绍Importance resampling。

Importance Resamping是计算统计学中从复杂分布生成样本的一种常用方法。它在文献4，2015年Talbot的硕士论文中充分阐述。主要思想是，由于生成\(g\) 的分布很复杂，我们先生成M个样本，再按照一定的权重从M中取N个样本，可以产生和\(g\)近似的分布。它的主要步骤是：

• 由于生成\(g\) 的分布很复杂或者并不归一化，我们选择另一个容易的分布 \(p\)，从概率分布函数\(p\)中选取M个样本candidate，得到\(X=\{x_1,x_2,...,x_M\}\)
• 在所有M个样本中，对任意第\(j\)个样本，均计算权重\(w_{j}=\frac{g\left(x_{j}\right)}{p\left(x_{j}\right)}\)
• 从M中生成N(N ≤ M)个样本：\(\{y_1,y_2,...,y_N\}\)，样本对应的权重\(w\)作为概率比例

这样生成的N个样本\(\{y_1,y_2,...,y_N\}\)和\(g\)的分布近似。

RIS(Resampled Importance Sampling)

套用Importance Resamping获得N个样本，来做蒙特卡洛积分的方法我们称之为 RIS。

由上文，蒙特卡洛积分可写作以下形式，需要的前提是\(g\)的样本容易获得且\(g\)的分布归一化。

\[L \approx \hat{L}_{M C}=\frac{1}{N} \sum_{i=1}^{N} \frac{f\left(y_{i}\right)}{g\left(y_{i}\right)} \]

首先，我们通过Importance Resamping获得关于分布\(g\)样本，Importance Resamping在\(g\)的分布不归一化时，也适用。Importance Resamping生成的样本近似于分布$g \(,为了维持蒙特卡洛积分的无偏性，必须引入一个权重函数\)\omega$，这个权重函数是M个Candidate，以及N个样本的函数，可写作：

\[\hat{L}_{r i s}=\frac{1}{N} \sum_{i=1}^{N} \frac{f\left(y_{i}\right)}{\hat{q}\left(y_{i}\right)} \cdot w^{*}\left(X_{1}, \ldots, X_{M}, y_{1}, \ldots, y_{N}\right) \]

推导(见附录)可得：

\[w^{*}\left(X_{1}, \ldots, X_{M}, y_{1}, \ldots, y_{N}\right)=\frac{1}{M} \sum_{j=1}^{M} w\left(x_{j}\right) \]

结合上述两个方程可得：

\[\hat{L}_{r i s}=\frac{1}{N} \sum_{i=1}^{N}\left(\frac{f\left(y_{i}\right)}{\hat{q}\left(y_{i}\right)}\right) \cdot \frac{1}{M} \sum_{j=1}^{M} w\left(x_{j}\right) \]

满足以下两个条件，可保证无偏，

• 在\(f\)的任意非零位置， \(g\)和 \(p\)都是正的。
• M和N均大于0

光线追踪中的应用

对于光线追踪求蒙特卡洛积分，被积函数\(L_{i}\left(x, \omega_{o}\right) f\left(\omega_{i}, \omega_{o}\right)\langle\cos \theta\rangle\)，计算生成M个Candidate，及其对应的\(\omega\)，这里N取1，每次取一个样本，通过RIS可获得关于被积函数的无偏估计。

Reservoir sampling蓄水池采样

蓄水池采样是一类采样算法，给定 M 个元素，一次性在其中随机选择 N个元素作为一个子集。通常，N是 定义为一个小的常数，M 通常非常大，对应的数据无法本地存储，或者M个元素是一个数据流。

基本方法和推导

假设数据序列的规模为M，或数据大小未知时，当前数据流一共通过了\(M_{sofar}\)，需要采样的数量的为 N。

• 首先构建一个可容纳 N 个元素的数组，将序列的前 N个元素放入数组中
• 然后从第 N+1 个元素开始，以\(N/M_{so far}\)的概率来决定该元素是否被替换到数组中,数组中被替换的概率相同
• 当遍历完所有元素之后，数组中剩下的N个元素即为所需采取的样本

推导如下：

持续不断的序列流过，对于蓄水池N个元素中第 i 个数（i≤N）:

• 在N步之前，被选中的概率为 1。
• 当走到第 N+1 步时，被第 N+1 个元素替换位置i处的概率为：N+1 个元素被选中的概率 * \(i\)号位被选中替换的概率，即为 \(\frac{N}{N+1} \times \frac{\mathbf{1}}{N}=\frac{1}{N+1}\)，则被保留的概率为

\[1-\frac{N}{N+1} \times \frac{\mathbf{1}}{N}=\frac{N}{N+1} \]

• 依次类推，不被 N+2 个元素替换的概率为:

\[1-\frac{N}{N+2} \times \frac{\mathbf{1}}{N}=\frac{N+1}{N+2} \]

• 则运行到第 n 步时，被保留的概率 = 被选中的概率 * 不被替换的概率，即：

\[1 \times \frac{N}{N+1} \times \frac{N+1}{N+2} \times \frac{N+2}{N+3} \times \ldots \times \frac{M-1}{M}=\frac{N}{M} \]

因此对于每个元素，被保留的概率都是\(N/M\).当M的数量不确定时，累计的数据流个数为\(M_{sofar}\), 蓄水池中每个元素的概率为\(N/M_{so far}\).

加权蓄水池采样

加权蓄水池采样是蓄水池采样算法的拓展，第$i \(个元素有对应的概率\)w_i\(，对应的第\)i \(个元素被保留的概率为\)\sum_{0}^{{i-1}w_{j}/\sum_{0}}w_{j}$。当蓄水池大小为1，即N = 1，对应计算的伪代码如下：

结合加权蓄水池采样的RIS

结合加权蓄水池采样的RIS采样比较直观，步骤如下：

• 每个像素、相邻像素、以及时域可复用的像素生成样本流
• 每次更新Reservoir中样本、权重和以及总的样本数
• 拿到更新后的Reservoir，根据RIS无偏估计，进行采样

实验结果

下面给出原始文献的数据，将应用了蓄水池流式采样的方法ReSTIR与2015年Talot的RIS同样时间所得到的效果做比较。可以看出利用蓄水池采样的方法，相比原有方法提升20%~30%。

参考文献

[1]Talbot J F. Importance resampling for global illumination[J]. 2005.

[2]Bitterli, Benedikt, et al. "Spatiotemporal reservoir resampling for real-time ray tracing with dynamic direct lighting." ACM Transactions on Graphics (TOG) 39.4 (2020): 148-1.

[3]Chris Wyman."WEIGHTED RESERVOIR SAMPLING:RANDOMLY SAMPLING STREAMS".Ray Tracing Gems II

[4]Justin F. Talbot. 2005. Importance Resampling for Global Illumination. Masters Thesis.Brigham Young University. https://diglib.eg.org/handle/10.2312/EGWR.EGSR05.139-146

附录

RIS采样无偏的证明：

由

\[E_{X Y}(X Y)=E_{X}\left(E_{Y}(Y \mid X) \cdot X\right) \]

可得：

\[E\left(\hat{L}_{r i s}\right)=E\left[E\left(\frac{1}{N} \sum_{i=1}^{N} \frac{f\left(Y_{i}\right)}{g\left(Y_{i}\right)} \mid X_{1}, \ldots, X_{M}\right) \cdot \frac{1}{M} \sum_{j=1}^{M} w\left(X_{j}\right)\right] \]

\[E\left(\hat{L}_{r i s}\right)=E\left[E\left(\frac{f(Y)}{g(Y)} \mid X_{1}, . ., X_{M}\right) \cdot \frac{1}{M} \sum_{j=1}^{M} w\left(X_{j}\right)\right] \]

由于Y是从样本里随机选出，因此可以写成下面的求和形式：

\[\begin{aligned} E\left(\hat{L}_{r i s}\right) &=E\left[\sum_{k=1}^{M}\left(\frac{f\left(X_{k}\right)}{g\left(X_{k}\right)} \cdot \frac{w\left(X_{k}\right)}{\sum_{j=1}^{M} w\left(X_{j}\right)}\right) \cdot \frac{1}{M} \sum_{j=1}^{M} w\left(X_{j}\right)\right] \\ &=E\left[\frac{1}{M} \sum_{k=1}^{M}\left(\frac{f\left(X_{k}\right)}{g\left(X_{k}\right)} \cdot w\left(X_{k}\right)\right)\right] \\ &=E\left(\frac{f(X)}{g(X)} \cdot w(X)\right) \end{aligned} \]