数据结构与算法
导航
目录
一、数据结构与算法概念
数据结构的定义
数据结构的概念:数据元素的集合,以及这些数据元素之间的关系,和它的构造方法
数据逻辑结构:
- 线性结构(1对1)
- 非线性结构(1对多)
算法
算法的5个重要特性
- 有穷性:执行有穷步之后结束,且每一步都可在有穷时间内完成。
- 确定性:算法中每一条指令都必须有确切的含义,不能含糊不清。
- 输入(>=0)
- 输出(>=1)
- 有效性(可行性):算法的每个步骤都能有效执行并能在执行有限次后例如a=0,b/a就无效得到确定的结果。
伪代码
伪代码:是一种算法描述语言,介于自然语言与编程语言之间,不用拘泥于具体的实现
二、线性表
线性表
线性表的概念:连续的序列(数据类型提相同)\(a_1,a_2,...,a_n\)
线性报常见的两种存储结构(物理结构)
- 顺序存储结构(顺序表)
- 优点:查找效率高
- 缺点:插入删除慢
- 可以随机访问表中任意节点
- 链式存储结构(单链表、循环链表、双向链表)
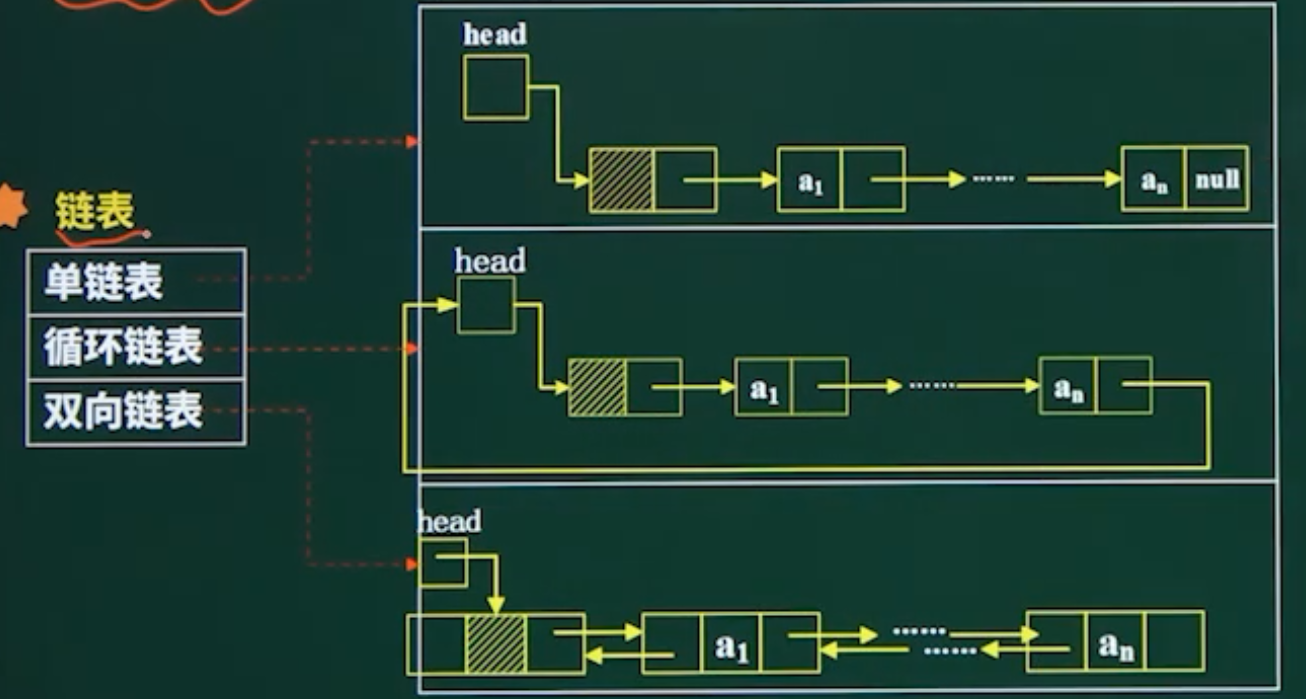
- 适合删除、插入操作,且不会移动元素
- 从头指针开始比对结点
- 链表的基本操作
- 单链表删除结点
- 单链表插入结点
- 双向链表删除结点
- 双向链表插入结点
三、队列与栈
栈
- 有栈顶和栈底
- 先进后出
队
- 有队尾和队头
- 先进先出
循环队列
- 为空head = tail
- 为满
- 留一个空,head =tail%max *size +1
把握出栈、入栈不同顺序来判断有哪些入栈顺序(可以入俩个,出一个之后再入一个,最后全出)
四、窜
广义表
广义表是n个表元素组成的有限序列,是线性表的推广
广义表长度
- 最外层括号去掉,逗号输+1就是长度(只需要数最外层的逗号)
- LS1=(a, (b, c), (d, e))
- =a, (b, c), (d, e)
- 现在共有4个逗号,但是不用加括号里面的逗号,所以长度是2+1=3
- LS1=(a, (b, c), (d, e))
广义表深度
- 深度就是最里面的括号是属于被包着的第几层括号
- LS1=(a, (b, c), (d, e))
- 这里的(b, c)和(d, e))外面还有一层括号,再加上它们本身的括号,所以深度=1+1=2
- LS1=(a, (b, c), (d, e))
窜
串是仅有字符构成的有限序列,是取值范围受限的线性表。
五、数组

- 注意上面公式是从0开始的(如果是从1开始的,那么结果-1)
- 巧记方法,题目说以行(或者列)存放的,那么就是用这个数据的行(或者列)*这个数组的列数(或者行数)+列数(或者行数)+起始地址
- 注意一下对应关系,它说行就拿行乘以列数,很简单识别的
六、树与二叉树
树
- 节点的度:它下边子树个数
- 树的高度::除开最底下叶子节点后,树的层数
- 叶子节点:树最下面的节点(不一定全在最下面的同一层)
- 分支节点:度数不为零的
- 内部节点:除开根节点以外的分支节点
- 父节点:子节点对应的根节点就是父节点
- 子节点子树就是子节点
- 兄弟节点:
- 层次
二叉树
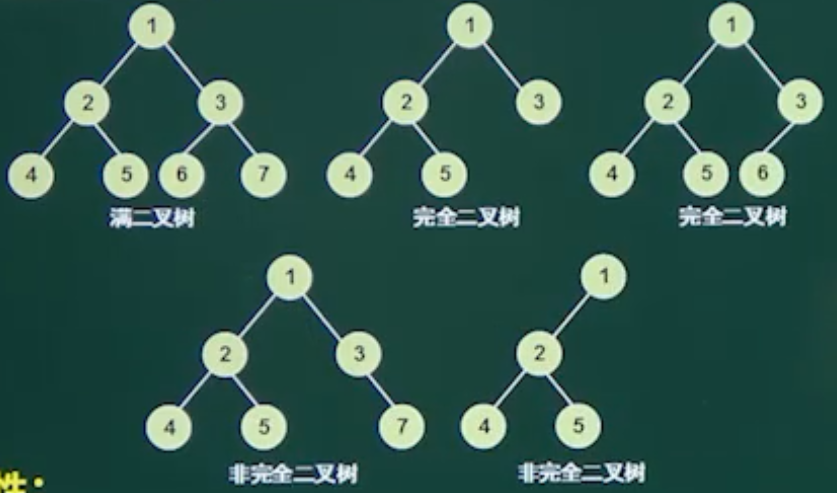
二叉树的重要特性:
- 在二叉树的第i层上最多有\(2^{k-1}\)个节点(\(i\geq1\))
- 深度为k的二叉树最多有\(2^{k-1}\)个节点(\(k\geq1\));
- 对任何一棵二叉树,如果其叶子节点数为\(n_0\),度为2的节点数为\(n_2\),则\(n_0\)=\(n_2\)+1。
- 如果对一颗有n个节点的完全二又树的节点按层序编号(从第1层到\(\lfloor log_2^{n}\rfloor+1\)层,每层从左到右),则对任一节点\(i(1\leq i\leq n)\),有
- 如果i=1,则节点i无父节点,是二叉树的根;如果\(i> 1\),则父节点是\(\lfloor i/2\rfloor;\)
- 如果\(2i>n\),则结点i为叶子节点,无左子节点;否则,其左子节点是节点2i;
- 如果2i+1>n,则节点i无右叶子节点,否则,其右子节点是节点2i+1.
二叉树遍历
- 前序遍历:根->左->右
- 中序遍历:左->根->右
- 后序遍历:左->右->根
- 层次遍历:从第一层开始,每一层从左到右
七、图
图的存储
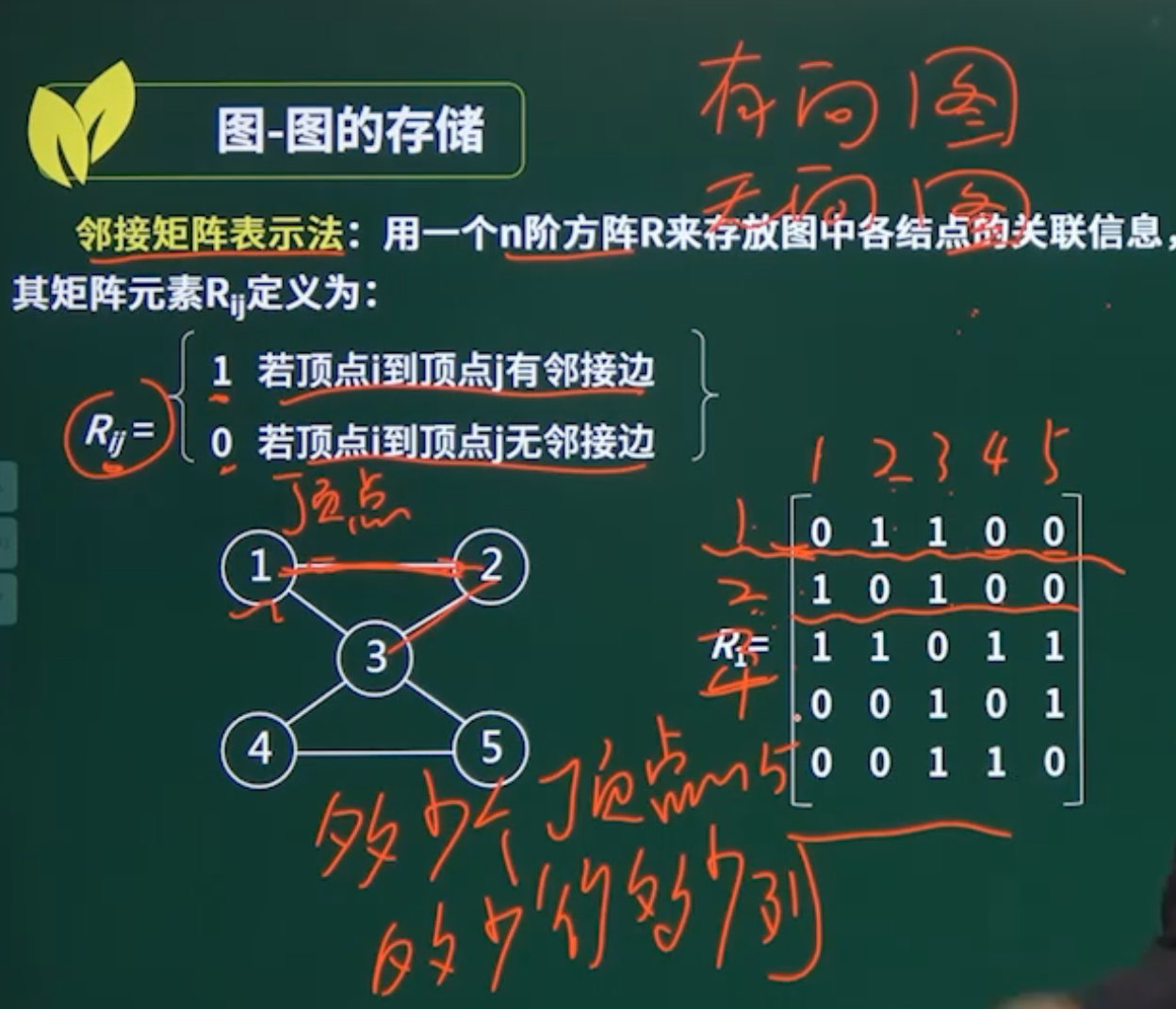
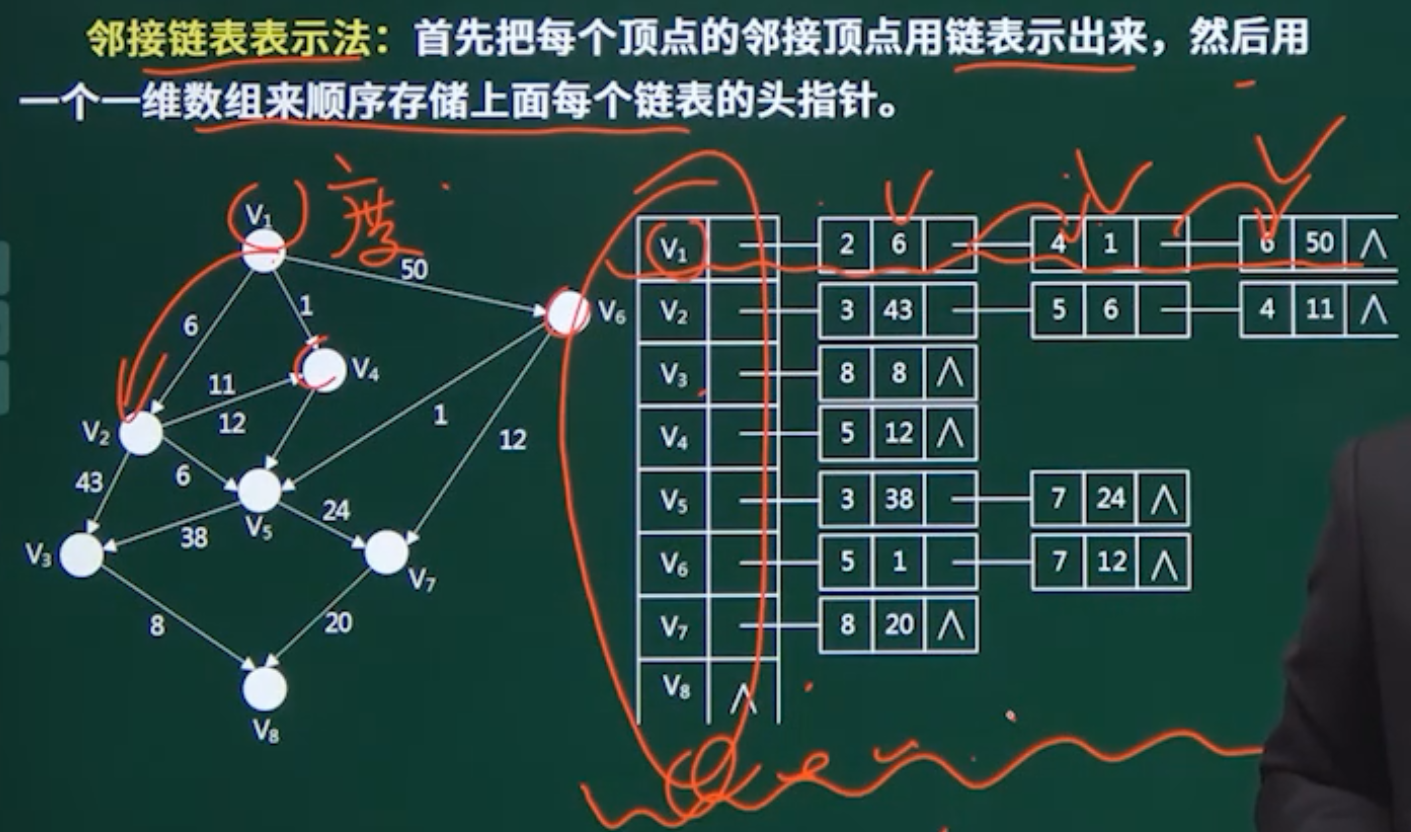

八、查找
五大查找
- 顺序表查找
- 顺序查找
- 二分查找
- 索引顺序查找
- 树表查找
- 二叉排序树
- 散列表查找
- 哈希查找
顺序查找
顺序查找的过程:将待查找的关键字为key的元素从头到尾与表中元素进行比较,如果中间存在关键字为key的元素,则返回成功;否则:则查找失败。
二分查找

二叉查找树(排序)

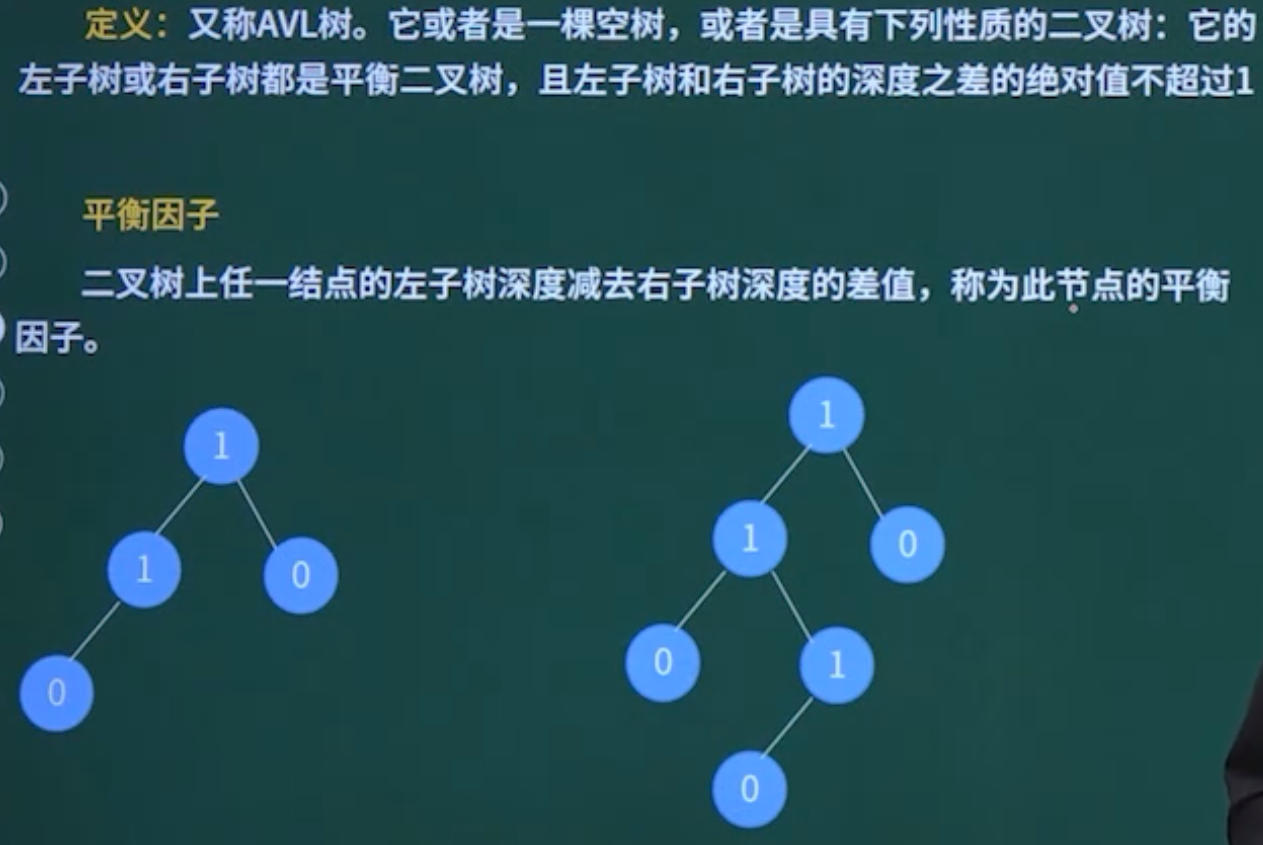
二叉平衡树
哈夫曼树

B-树

B+树

散列表




