虚树
好久以前开的坑,填一下
构树的部分不难,需要会在上面dp
板子:

//记得调用dfs(1,0)和process() //倍增的部分可以用log而不是19来卡常 int tot,id[N]; int dep[N],sz[N],to[N][20]; inline bool cmp(int x,int y) { return id[x]<id[y]; } void dfs(int x,int fa) { sz[x]=1; id[x]=++tot; to[x][0]=fa; dep[x]=dep[fa]+1; for(int i=0;i<v[x].size();i++) { int y=v[x][i]; if(y!=fa) { dfs(y,x); sz[x]+=sz[y]; } } } void process() { for(int i=1;i<20;i++) for(int j=1;j<=n;j++) to[j][i]=to[to[j][i-1]][i-1]; } inline int lca(int x,int y) { if(dep[x]<dep[y]) swap(x,y); for(int i=19;i>=0;i--) if(dep[to[x][i]]>=dep[y]) x=to[x][i]; for(int i=19;i>=0;i--) if(to[x][i]!=to[y][i]) x=to[x][i],y=to[y][i]; return (x==y?x:to[x][0]); } //a: 按照dfs序排好序的有用点 int a[N]; //st: 手动栈 int top,st[N]; //nodes: 用于清空 vt: 虚树 vector<int> nodes,vt[N]; void clear() { top=0; for(int i=0;i<nodes.size();i++) { int cur=nodes[i]; in[cur]=ans[cur]=near[cur]=0; vt[cur].clear(); } nodes.clear(); } void add_node(int x) { st[++top]=x; nodes.push_back(x); } void add_edge(int x) { vt[x].push_back(st[top]); top--; } void build() { add_node(1); for(int i=1;i<=m;i++) { int anc=lca(a[i],st[top]); while(top>1 && dep[anc]<dep[st[top-1]]) add_edge(st[top-1]); if(dep[anc]<dep[st[top]]) add_edge(anc); if(anc!=st[top]) add_node(anc); if(h[i]!=st[top]) add_node(a[i]); } while(top>1) add_edge(st[top-1]); }
~ 简介 ~
虚树,就是将树上的有用节点及其LCA提出来,重新构建的一棵树
一般解决的是这种问题:给定一棵树,每次询问关于树上$m_i$个点的问题,且保证$\sum m_i<1\times 10^5$(差不多是这个数量级)
~ 建树 ~
建树的方法有很多种,不过在实际情况中最常用、简洁的办法 是通过栈来实现
考虑用dfs序给树上的节点重新标号
对于所有有用节点,按照dfs序从小到大在虚树上依次加入
在加入节点的过程中,维护一个栈
从栈顶到栈底,依次是 上一个有用节点到根节点的路径上,所有在虚树中的节点
为了避免出错,我们可以强制将根节点加入虚树;那么在初始情况下,栈中只有一个根节点
现在考虑如何新加入一个有用节点
此时虚树的情况大概是这样:
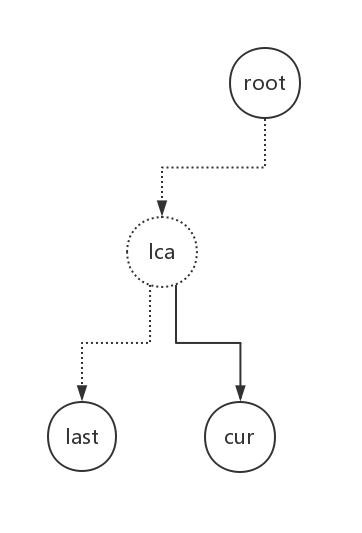
我们需要向虚树中加入两个节点:当前有用节点、以及与上一个有用节点的LCA
假如这个LCA已经在虚树中了,那么可以直接将栈弹到LCA,然后加入当前点
假如这个LCA不在当前的虚树中,那么需要将栈弹到第一个比LCA浅的点,然后加入LCA、加入当前点
而虚树中的边是在出栈的时候添加的,因为此时虚树中的父子关系是确定的;如果在入栈的时候就加边,那么就无法处理上面所说的 LCA不在当前虚树中 的情况
那么现在只有两种情况下会加边:
1. 弹出栈顶时:将栈中从栈顶至栈底的第$2$个节点向第$1$个节点连边
2. 加入LCA前:将LCA向栈中第一个比LCA深的点连边
要记得将最后栈中的剩余节点弹出来
void add_node(int x) { st[++top]=x; nodes.push_back(x); } void add_edge(int x) { vt[x].push_back(st[top]); top--; } void build() { add_node(1); for(int i=1;i<=m;i++) { int anc=lca(h[i],st[top]);//h数组中存的是按dfs序排序后的有用节点 while(top>1 && dep[anc]<dep[st[top-1]]) add_edge(st[top-1]); if(dep[anc]<dep[st[top]]) add_edge(anc); if(anc!=st[top]) add_node(anc); if(h[i]!=st[top]) add_node(h[i]); } while(top>1) add_edge(st[top-1]); }
~ 一些题目 ~
也是个人感觉从易到难
CF 613D ($Kingdom\ and\ its\ Cities$)
很常规的虚树题,在虚树上面dp
对于虚树上的每个点,考虑是否截断其通向儿子的边
若当前节点是关键点,那么将儿子中需要被分割的节点全部分割;该点对于上一层视为需要被分割的点
若当前节点不是关键点,那么分为三种情况
1. 儿子中不存在需要被分割的点,那么不需要在当前点分割;该点对上一层视为不需要被分割的点
2. 儿子中只有一个需要被分割的点,那么不需要在当前点分割;该点对上一层视为需要被分割的点
3. 儿子中有超过一个需要被分割的点,那么在当前点分割;该点对上一层视为不需要被分割的点

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int N=100005; int n,m,q; vector<int> v[N]; int tot,id[N],dep[N]; int to[N][20]; void dfs(int x,int fa) { id[x]=++tot; to[x][0]=fa; dep[x]=dep[fa]+1; for(int i=0;i<v[x].size();i++) { int nxt=v[x][i]; if(nxt!=fa) dfs(nxt,x); } } inline int lca(int x,int y) { if(dep[x]<dep[y]) swap(x,y); for(int i=19;i>=0;i--) if(dep[to[x][i]]>=dep[y]) x=to[x][i]; for(int i=19;i>=0;i--) if(to[x][i]!=to[y][i]) x=to[x][i],y=to[y][i]; return (x==y?x:to[x][0]); } int a[N]; inline bool cmp(int x,int y) { return id[x]<id[y]; } int sz[N],dp[N]; vector<int> nodes,vt[N]; void clear() { for(int i=0;i<nodes.size();i++) { sz[nodes[i]]=dp[nodes[i]]=0; vt[nodes[i]].clear(); } nodes.clear(); } int top,st[N]; void add_node(int x) { st[++top]=x; nodes.push_back(x); } void add_edge(int x) { vt[x].push_back(st[top]); top--; } void build() { if(!top) add_node(1); for(int i=1;i<=m;i++) { int anc=lca(st[top],a[i]); while(top>1 && dep[anc]<dep[st[top-1]]) add_edge(st[top-1]); if(dep[anc]<dep[st[top]]) add_edge(anc); if(anc!=st[top]) add_node(anc); if(a[i]!=st[top]) add_node(a[i]); } while(top>1) add_edge(st[top-1]); top--; } void solve(int x) { int cnt=0; for(int i=0;i<vt[x].size();i++) { int nxt=vt[x][i]; solve(nxt); cnt+=sz[nxt]; dp[x]+=dp[nxt]; } if(sz[x]) dp[x]+=cnt; else if(cnt>1) dp[x]++; else sz[x]=cnt; } int main() { scanf("%d",&n); for(int i=1;i<n;i++) { int x,y; scanf("%d%d",&x,&y); v[x].push_back(y); v[y].push_back(x); } dfs(1,0); for(int i=1;i<20;i++) for(int j=1;j<=n;j++) to[j][i]=to[to[j][i-1]][i-1]; scanf("%d",&q); while(q--) { clear(); scanf("%d",&m); bool flag=false; for(int i=1;i<=m;i++) scanf("%d",&a[i]),sz[a[i]]=1; for(int i=1;i<=m;i++) if(sz[to[a[i]][0]]) flag=true; if(flag) { printf("-1\n"); for(int i=1;i<=m;i++) sz[a[i]]=0; continue; } sort(a+1,a+m+1,cmp); build(); solve(1); printf("%d\n",dp[1]); } return 0; }
CF Gym 102220D ($Master\ of\ Data\ Structure$,$2019$东北省赛)
把所有操作中的$u,v$全部拿出来建树,那么虚树中只有不超过$8000$个点;在上面暴力就可以了
不过这题中有两个非常规的地方:
建树的时候反向连边比较方便(较深的连向较浅的),因为对于路径操作时要分别从$u,v$爬到LCA
还有,对于每条虚树中的边也要维护权值(边上所省略的点都是同一权值)

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=500005; const int M=4005; int n,m; vector<int> v[N]; int tot,id[N]; int dep[N],to[N][20]; inline bool cmp(int x,int y) { return id[x]<id[y]; } void dfs(int x,int fa) { id[x]=++tot; to[x][0]=fa; dep[x]=dep[fa]+1; for(int i=0;i<v[x].size();i++) { int nxt=v[x][i]; if(nxt!=fa) dfs(nxt,x); } } void process() { for(int i=1;i<20;i++) for(int j=1;j<=n;j++) to[j][i]=to[to[j][i-1]][i-1]; } inline int lca(int x,int y) { if(dep[x]<dep[y]) swap(x,y); for(int i=19;i>=0;i--) if(dep[to[x][i]]>=dep[y]) x=to[x][i]; for(int i=19;i>=0;i--) if(to[x][i]!=to[y][i]) x=to[x][i],y=to[y][i]; return (x==y?x:to[x][0]); } int top,st[N]; vector<int> nodes; int etot,eid[N],vfa[N]; void clear() { top=etot=0; for(int i=0;i<nodes.size();i++) vfa[nodes[i]]=eid[nodes[i]]=0; nodes.clear(); } void add_edge(int x) { vfa[st[top]]=x; eid[st[top]]=++etot; top--; } void build() { st[++top]; for(int i=0;i<nodes.size();i++) { int anc=lca(nodes[i],st[top]); while(top>1 && dep[anc]<dep[st[top-1]]) add_edge(st[top-1]); if(dep[anc]<dep[st[top]]) add_edge(anc); if(anc!=st[top]) st[++top]=anc; if(nodes[i]!=st[top]) st[++top]=nodes[i]; } while(top>1) add_edge(st[top-1]); } int opt[M],U[M],V[M],K[M]; ll val[N+M*2]; ll modify(ll x,int k,int opt) { if(opt==1) return x+k; if(opt==2) return x^k; if(opt==3) return (x<k?x:x-k); } void modify(int x,int y,int k,int opt) { int anc=lca(x,y),arr[2]={x,y}; for(int i=0;i<2;i++) { x=arr[i]; while(x!=anc) { val[x]=modify(val[x],k,opt); val[n+eid[x]]=modify(val[n+eid[x]],k,opt); x=vfa[x]; } } val[anc]=modify(val[anc],k,opt); } ll sum,xorsum,maxv,minv,minabs; void update(ll x,int k,int num) { sum+=1LL*num*x; xorsum^=(num%2*x); maxv=max(maxv,x); minv=min(minv,x); minabs=min(minabs,abs(x-k)); } ll query(int x,int y,int k,int opt) { sum=0,xorsum=0,maxv=0,minv=1<<30,minabs=1<<30; int anc=lca(x,y),arr[2]={x,y}; for(int i=0;i<2;i++) { x=arr[i]; while(x!=anc) { int fa=vfa[x],e=n+eid[x],num=dep[x]-dep[fa]-1; update(val[x],k,1); if(num) update(val[e],k,num); x=fa; } } update(val[anc],k,1); if(opt==4) return sum; if(opt==5) return xorsum; if(opt==6) return maxv-minv; if(opt==7) return minabs; } int main() { int T; scanf("%d",&T); while(T--) { tot=0; for(int i=1;i<=n;i++) v[i].clear(); memset(val,0LL,sizeof(val)); clear(); scanf("%d%d",&n,&m); for(int i=1;i<n;i++) { int x,y; scanf("%d%d",&x,&y); v[x].push_back(y); v[y].push_back(x); } dfs(1,0); process(); for(int i=1;i<=m;i++) { scanf("%d%d%d",&opt[i],&U[i],&V[i]); nodes.push_back(U[i]); nodes.push_back(V[i]); if(opt[i]<4 || opt[i]>6) scanf("%d",&K[i]); } sort(nodes.begin(),nodes.end(),cmp); build(); for(int i=1;i<=m;i++) if(opt[i]<=3) modify(U[i],V[i],K[i],opt[i]); else printf("%lld\n",query(U[i],V[i],K[i],opt[i])); } return 0; }
Luogu P3233 (世界树,$HNOI2014$)
应该是标准难度的虚树题?难在dp上
我们将原树的关键点抽成虚树时,其实只能维护很少的一些信息:不外乎子树大小和父子关系
所以,遇到这种题目时,就要考虑怎么用有限的信息处理所有查询
首先考虑不在虚树上的点:其实我们完全没有办法处理他们,特别是那种不在虚树边上的点(虚树边上的点伸出来的子树中)
所以,他们一定可以不需要处理(笑)
在这一题中,我们总可以将原树中所有的点简化为两种:要不在虚树中,要不在虚树的边上

即,将从虚树边(两虚树端点在原树上的路径)上伸出去的点全部合并到虚树边上;这可以用子树大小$sz[i]$相减来得到
那么现在只要考虑虚树边上所有点的归属问题
肯定可以将这条路径从中间截开,靠上的一部分与上端点归属相同,靠下的一部分与下端点归属相同
那么我们就需要求出这个分割的位置
考虑先通过两次dfs(先从下到上,再从上到下)求出每个虚树节点的归属点和到归属点的距离
那么考虑从每条虚树边从下端点向上走,一开始到两个归属点的距离值之差为$diff$
沿着路径每向上走一次,离下归属点的距离就$+1$、离上归属点的距离就$-1$,那么会使得$diff$减$2$
于是分割的位置就是从下端点向上走$\frac{diff}{2}$步的节点(自己手推一下,注意$diff$的奇偶性),那么倍增上去就好了
(不知道为什么常数这么大...可能是滥用vector?)

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int N=300005; int n,m,q; vector<int> v[N]; int tot,id[N]; int dep[N],sz[N],to[N][20]; inline bool cmp(int x,int y) { return id[x]<id[y]; } void dfs(int x,int fa) { sz[x]=1; id[x]=++tot; to[x][0]=fa; dep[x]=dep[fa]+1; for(int i=0;i<v[x].size();i++) { int y=v[x][i]; if(y!=fa) { dfs(y,x); sz[x]+=sz[y]; } } } void process() { for(int i=1;i<20;i++) for(int j=1;j<=n;j++) to[j][i]=to[to[j][i-1]][i-1]; } inline int lca(int x,int y) { if(dep[x]<dep[y]) swap(x,y); for(int i=19;i>=0;i--) if(dep[to[x][i]]>=dep[y]) x=to[x][i]; for(int i=19;i>=0;i--) if(to[x][i]!=to[y][i]) x=to[x][i],y=to[y][i]; return (x==y?x:to[x][0]); } int h[N]; int top,st[N]; int in[N],ans[N],dist[N],near[N]; vector<int> nodes,vt[N]; void clear() { top=0; for(int i=0;i<nodes.size();i++) { int cur=nodes[i]; in[cur]=ans[cur]=near[cur]=0; vt[cur].clear(); } nodes.clear(); } void add_node(int x) { st[++top]=x; nodes.push_back(x); } void add_edge(int x) { vt[x].push_back(st[top]); top--; } void build() { add_node(1); for(int i=1;i<=m;i++) { int anc=lca(h[i],st[top]); while(top>1 && dep[anc]<dep[st[top-1]]) add_edge(st[top-1]); if(dep[anc]<dep[st[top]]) add_edge(anc); if(anc!=st[top]) add_node(anc); if(h[i]!=st[top]) add_node(h[i]); } while(top>1) add_edge(st[top-1]); } int a[N]; void pushup(int x) { if(in[x]) dist[x]=0,near[x]=x; for(int i=0;i<vt[x].size();i++) { int y=vt[x][i]; pushup(y); int D=dep[near[y]]-dep[x]; if(!near[x] || D<dist[x] || (D==dist[x] && near[y]<near[x])) dist[x]=D,near[x]=near[y]; } } void pushdown(int x) { for(int i=0;i<vt[x].size();i++) { int y=vt[x][i]; int D=dist[x]+dep[y]-dep[x]; if(D<dist[y] || (D==dist[y] && near[x]<near[y])) dist[y]=D,near[y]=near[x]; pushdown(y); } } inline int getson(int x,int y) { for(int i=19;i>=0;i--) if(dep[to[y][i]]>dep[x]) y=to[y][i]; return y; } inline int dis(int x,int y) { int anc=lca(x,y); return dep[x]+dep[y]-dep[anc]*2; } void solve(int x) { ans[near[x]]+=sz[x]; for(int i=0;i<vt[x].size();i++) { int y=vt[x][i],son=getson(x,y); ans[near[x]]-=sz[son]; int tsz=sz[son]-sz[y]; if(near[x]==near[y]) ans[near[x]]+=tsz; else { int diff=dis(y,near[x])-dist[y]; int mid=y; for(int j=19;j>=0;j--) if((diff>>j)&2) mid=to[mid][j]; int dsz,usz,rem=0; if(diff&1) dsz=sz[mid]-sz[y],usz=tsz-dsz; else { dsz=sz[getson(mid,y)]-sz[y],usz=sz[son]-sz[mid]; rem=tsz-dsz-usz; if(near[x]<near[y]) usz+=rem; else dsz+=rem; } ans[near[x]]+=usz; ans[near[y]]+=dsz; } solve(y); } } int main() { scanf("%d",&n); for(int i=1;i<n;i++) { int x,y; scanf("%d%d",&x,&y); v[x].push_back(y); v[y].push_back(x); } dfs(1,0); process(); scanf("%d",&q); while(q--) { clear(); scanf("%d",&m); for(int i=1;i<=m;i++) { scanf("%d",&a[i]); in[a[i]]=1,h[i]=a[i]; } sort(h+1,h+m+1,cmp); build(); pushup(1); pushdown(1); solve(1); for(int i=1;i<=m;i++) printf("%d",ans[a[i]]),putchar(i==m?'\n':' '); } return 0; }
虚树也就是一个工具而已,关键是怎么在上面操作
一些其他的题目(如果有的话)就补在下面了
Nowcoder 5666B (Infinite Tree,2020牛客暑期多校第一场)
不是对已有树建虚树,而是直接根据性质建,挺有收获的。
2022 ICPC南京 E
首先我们可以看出需要对整棵树的每一层分别处理。那么我们尝试对于每一层计算答案,发现需要在 这一层的“叶子”及其祖先构成的树上 进行树形DP(这个转移很显然就不细说了),这样暴力转化后计算的复杂度是 $\mathcal{O}(n^2)$ 的。
考虑在此之上优化,一个很显然的想法就是转移到这一层“叶子”构成的虚树上进行DP,发现转移的代价是可以通过ST表预处理 $\mathcal{O}(1)$ 得到的(一段区间的min)。那么转而在虚树上DP就能解决了,复杂度为 $\mathcal{O}(n\log n)$。题目很传统,整体思路也很自然,赛场上十分钟左右就想出来了。
(完)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号