后缀树

 

后缀树算是后缀数组与后缀自动机的综合形态，兼具两类后缀结构的特点。但同时，后缀树又能分别用这两种后缀结构实现，并不一定需要去学对应的算法。

所以在真正做题时，我们可以从后缀树的角度进行思考，从而利用其结构来分析能够用于解题的性质，然后再采用后缀数组或后缀自动机进行实现。在处理字典序相关问题时，后缀树具有一定优势。不过后缀树是离线构造的，对于在线问题求解起来比较困难。

本文部分借鉴了 Luckyblock - 「笔记」后缀树 的思路。

 

 

~ 后缀树的定义 ~

 

对于一个字符串 $s[1:n]$，其后缀树可以通过三步暴力构造：

(1) 在字符串的末尾加上一个特殊字符，记为“\$”；

(2) 取出其不为“\$”的全部 $n$ 个后缀 $s[n:n+1],\ s[n-1:n+1],\ ...,\ s[1:n+1]$，依次插到 trie 树上去；

(3) 将 trie 树上的长度超过一的链合并成一条边。

 

以字符串 $s=banana$ 为例，首先我们在加过特殊字符后，将其后缀 a\$，na\$，ana\$，nana\$，anana\$，banana\$ 插入到 trie 上，结果如下图所示：

 

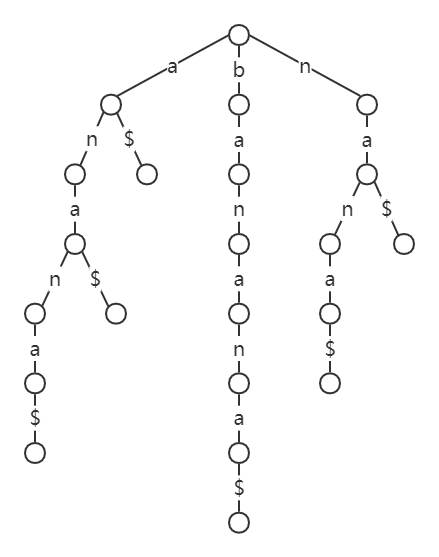
接着，我们将所有的长度超过一的链（标红部分）合并成一条边，将链上的字母顺序写到合并后的边上：

即可得到 banana 的后缀树。

上述的做法是 $\mathrm{O}(n^2)$ 的。虽然存在一种 $\mathrm{O}(n)$ 的后缀树建树算法 Ukkonen，但本文并不准备作介绍；而是通过分析后缀树与后缀树组、后缀自动机的联系，从而在已经求得后缀数组或后缀自动机的情况下快速构建后缀树。转化的复杂度均为 $\mathrm{O}(n)$。

 

 

~ 后缀树与后缀数组 ~

 

根据后缀树的定义，其每个叶节点对应着 $s$ 的一个后缀。

假如对于后缀树同一节点的所有转移，我们按照转移的第一个字母排序来规定访问的先后顺序（此时认为特殊字符 \$ 小于所有字母），那么我们可以从根节点开始进行 dfs。接着，我们将所有叶节点按照 dfs 序进行排序。以上面的 banana 为例，dfs 序从小到大的叶节点对应子串依次为 a\$，ana\$，anana\$，banana\$，na\$，nana\$。

可以发现，这些子串在 dfs 序从小到大的同时，字典序也是从小到大的，于是恰好能够对应后缀树组中的 $sa[i]$。对于字典序相邻的两个后缀 $sa[i]$ 与 $sa[i+1]$，我们利用后缀数组能够处理出 $height[i]=\mathrm{LCP}(s[sa[i]:n], s[sa[i+1]:n])$，其对应着两个叶节点在后缀树上 LCA 的深度。

于是我们可以通过将每个后缀按照字典序大小依次插入到虚树中来构建后缀树。如果对于虚树有不了解的可以参照虚树的笔记。我们维护一个当前链的单调栈，依次尝试插入后缀 $sa[i]$。

假如 $height[i-1]=n-sa[i-1]+1$，即 $\mathrm{LCP}(s[sa[i-1]:n],s[sa[i]:n])=s[sa[i-1]:n]$，那么直接将后缀 $sa[i]$ 加入单调栈即可（此时在后缀树中，$sa[i]$ 是 $sa[i-1]$ 的子孙）；

否则，有 $height[i-1]<n-sa[i-1]+1$，此时会产生分叉，我们就需要一直弹栈、直到栈顶对应子串长度小于等于 $height[i-1]$，再将 $sa[i]$ 加入单调栈（当弹栈后栈顶子串长度小于 $height[i-1]$ 时，还需要先插入 $sa[i-1]$ 与 $sa[i]$ 的 LCP）。

感觉用后缀数组来建立后缀树有点麻烦，就不给出实现的代码了。用后缀自动机在实现上更简单一点。

 

 

~ 后缀树与后缀自动机 ~

 

有一个很神奇的结论：后缀树的结构 等价于 反转字符串 $s$ 后建立的 parent 树。

我们通过画 $s=banana$ 的图来会意一下，左图是后缀树，右图是反串的 parent 树：

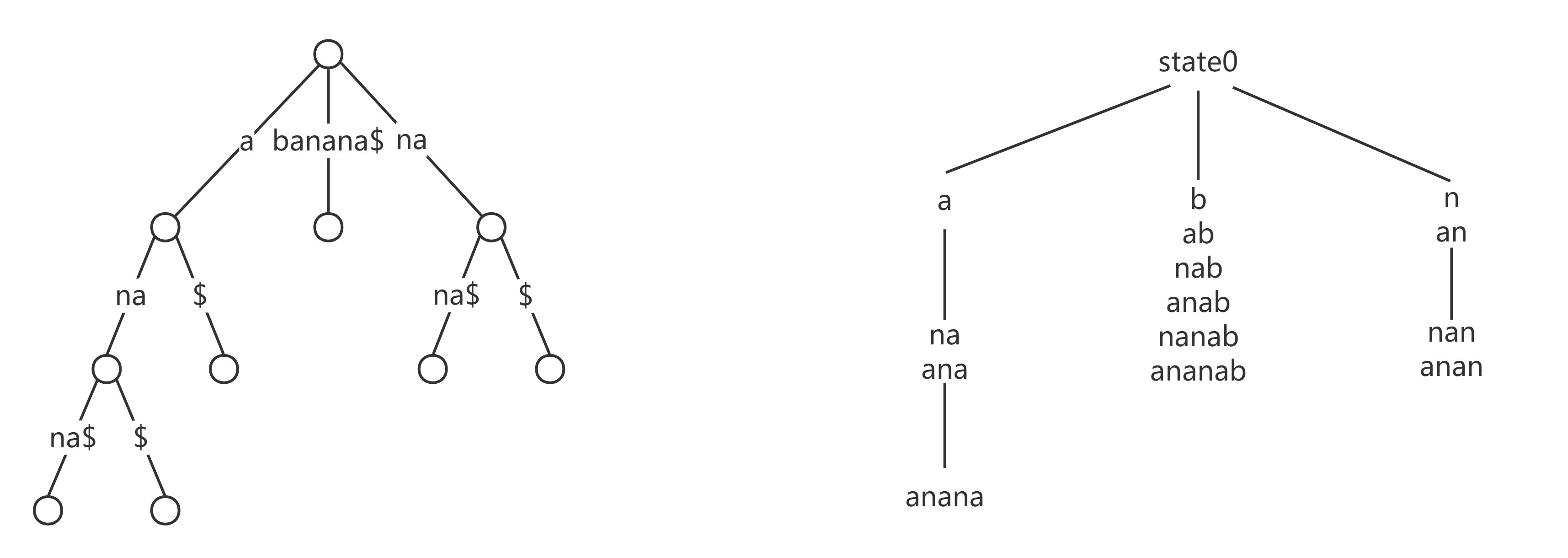
感觉还是有点差距？那么我们考虑把后缀树的特殊字符 \$ 收缩一下。

对于只有单独一个特殊字符的转移边，我们将该边删去、同时将其父节点标记为终止节点；对于包含特殊字符且长度大于 $1$ 的转移边，我们保留该边、并将其子节点标记为终止节点。经过这样的等价转化后，我们得到了下图（终止节点标记为红色）：

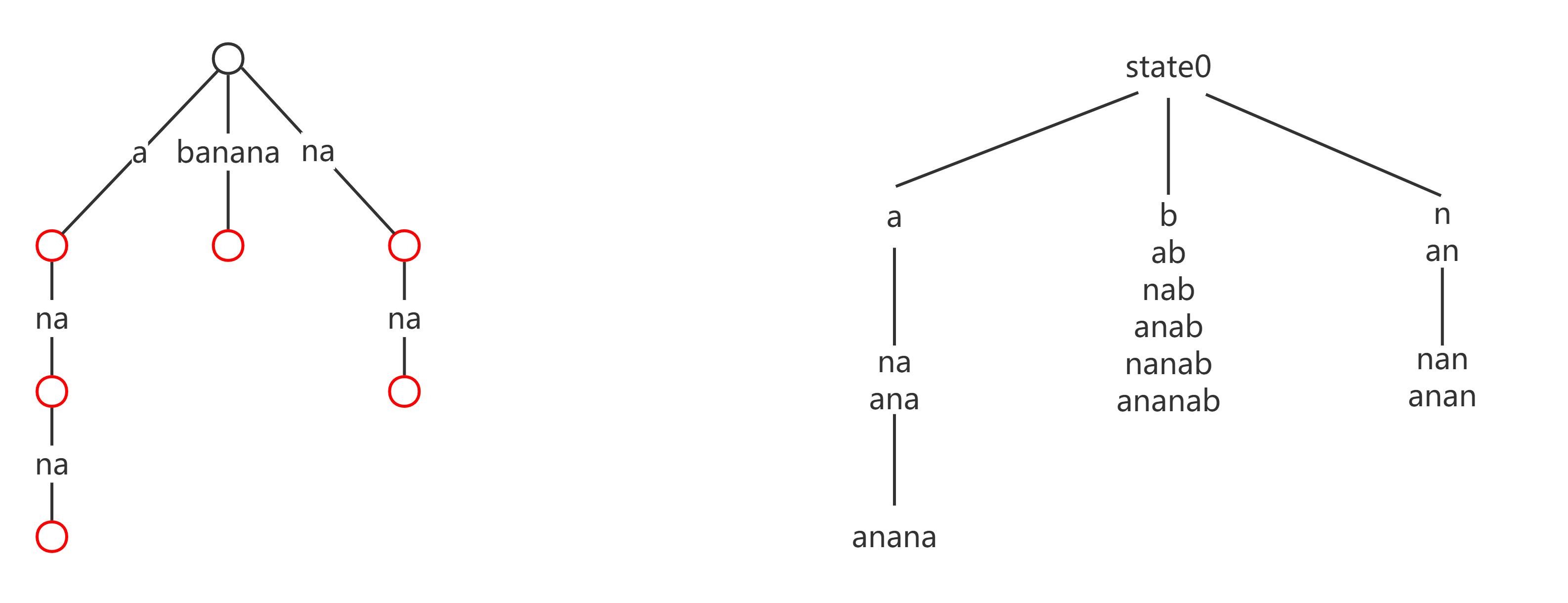
是不是有内味儿了？接着，我们对于反串的 parent 树按照这样的规则来规定转移边：我们将 $\mathrm{longest}(x)$ 与 $\mathrm{longest}(\mathrm{link}(x))$ 相差的字符，依次添加到转移边上。比如，对于状态 $\{na,ana\}$，其 $\mathrm{link}$ 为状态 $\{a\}$，为了让 a 变成 ana，我们依次在最前面添加了字符 n、a（即 $a \rightarrow \underline{n}a \rightarrow \underline{a}na$），于是 $\{a\}$ 到 $\{na,ana\}$ 的转移边就为 na。按照这个规则，我们标记一下 parent 树的转移边，如下（为了便于区分状态与边，将转移边标橙）：

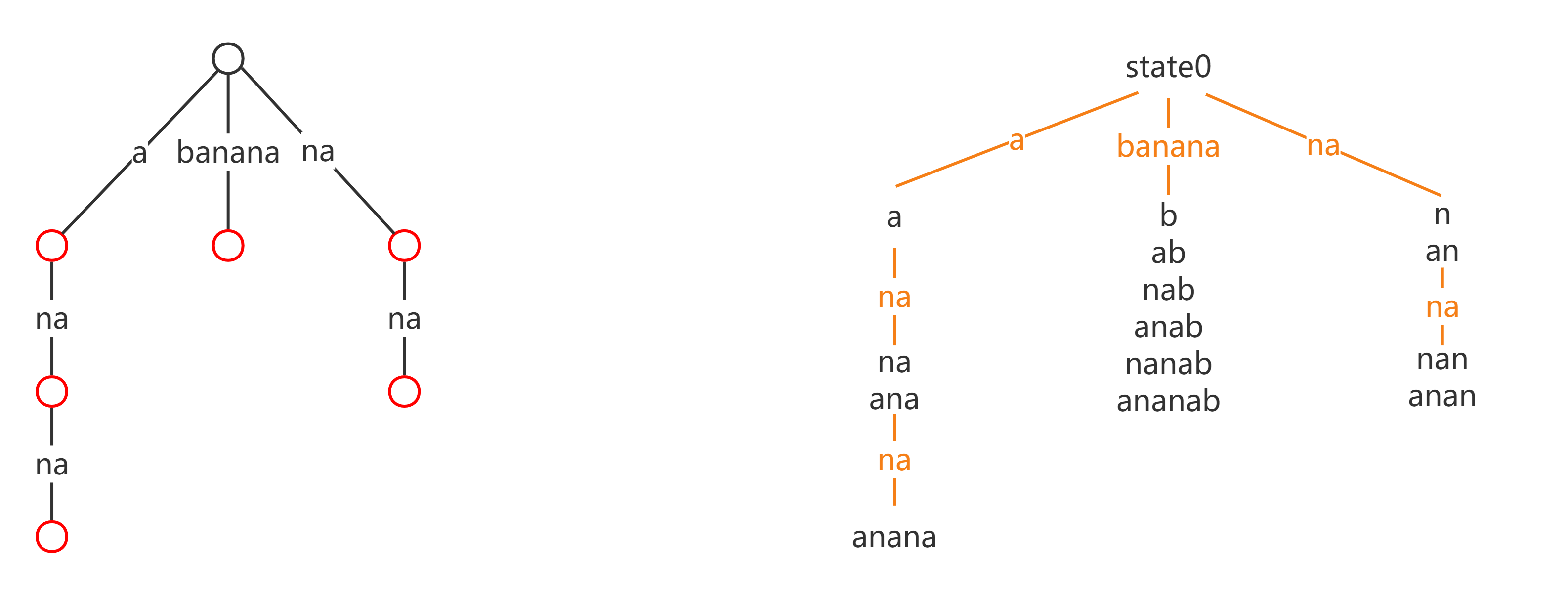
完全一致了！

尝试分析了一通，感觉很难用简洁的语言证明两者等价，就咕了罢。

具体讲讲如何利用反串的 parent 树建立后缀树。由于每个 SAM 状态直接对应了后缀树上的节点，因此我们只需要构造出转移边就可以了。我们记 $endpos[x]$ 为状态 $x$ 的在字符串上的任意出现位置（一般维护的是最大或最小的位置，由于是反串，故需要对应取 min 或 max），那么一个由 $\mathrm{link}(x)$ 到 $x$ 的转移就是子串 $s[endpos[x]-\mathrm{len}(x)+1:endpos[x]-\mathrm{len}(\mathrm{link}(x))]$ 的反串。

 

 

~ 后缀树的性质 ~

 

1. 节点数不超过 $2n$。这个性质无论从后缀数组还是后缀自动机的角度都很显然。

2. 从根到（将缩链展开后）每个节点的路径与 $s$ 每个本质不同的子串一一对应。根据后缀树的暴力构建方法看就很显然，因为相当于枚举了每一个子串的起点，并一直插到 $s$ 的末尾。假如一个串出现了多次，在构建 trie 树的时候就不会新建节点了。

3. 后缀树上 LCA 与后缀树组 $height$ 的对应关系。所以在一些情况下不用显式建树，直接用 $height$ 就能解决问题。

4. parent 树上的一些性质，比如对于每个点暴力往上跳到根的复杂度为 $\mathrm{O}(n^{1.5})$。

 

 

~ 例题 ~

 

CodeforcesGym 103409J Suffix Automaton（2021 CCPC 桂林）【后缀树性质】

首先，我们肯定是要对于不同长度的子串分别处理的。至于统计每个长度的本质不同子串数量，由于一个 SAM 的状态对应了长度范围在 $[\mathrm{len}(\mathrm{link}(x))+1,\mathrm{len}(x)]$ 的子串各一个，所以对于两端点差分一下即可。

现在问题就变成了求长度为 $x$ 的子串中字典序为 $y$ 的串，我们只需要定位到其出现在哪条后缀树边上即可回答查询。首先我们对于后缀树上的边进行一遍 dfs，就可以确定每条边对应的子串们的字典序大小。对于后缀树上的一条边，其在一定的深度范围内才有效，其余时间无效，我们可以用树状数组上的 0 / 1 来维护是否有效。那么我们对于长度做扫描线，当扫到长度 $x$ 时，我们查找目前有效的边中第 $y$ 小的，就能找到答案子串所在的边，这可以通过树状数组上二分 $\mathrm{O}(n\ logn)$ 做到。

#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;

typedef long long ll;
typedef pair<int,int> pii;

const int M=(1<<22)+5;

int t[M],_log=22;

inline int lowbit(int x)
{
    return x&(-x);
}

inline void add(int k,int x)
{
    for(int i=k;i<M;i+=lowbit(i))
        t[i]+=x;
}

inline int sum(int k)
{
    int ans=0;
    for(int i=k;i;i-=lowbit(i))
        ans+=t[i];
    return ans;
}

inline int kth(int k)
{
    int pos=1<<_log;
    for(int i=_log-1;i>=0;i--)
        if(t[pos-(1<<i)]>=k)
            pos-=(1<<i);
        else
            k-=t[pos-(1<<i)];
    return pos;
}

const int N=1000005;
const int C=26; //注意检查字符集大小！

//在结构题外开任何与SAM状态相关的数组，都需要N<<1
struct SuffixAutomaton
{
    int sz,lst; //状态数上限=2|S|-1 
    
    int len[N<<1],link[N<<1];
    int nxt[N<<1][C];
    //map<char,int> nxt[N<<1];
    //extend(char)，并使用nxt[clone]=nxt[q]替换memcpy
    
    SuffixAutomaton()
    {
        len[0]=0,link[0]=-1;
        lst=sz=0;
    }
    
    void extend(int c)
    {
        int cur=++sz;
        len[cur]=len[lst]+1;
        
        int p=lst;
        while(p!=-1 && !nxt[p][c])
            nxt[p][c]=cur,p=link[p];
        
        if(p==-1)
            link[cur]=0;
        else
        {
            int q=nxt[p][c];
            if(len[p]+1==len[q])
                link[cur]=q;
            else
            {
                int clone=++sz;
                len[clone]=len[p]+1;
                link[clone]=link[q];
                memcpy(nxt[clone],nxt[q],C*4);
                
                while(p!=-1 && nxt[p][c]==q)
                    nxt[p][c]=clone,p=link[p];
                link[q]=link[cur]=clone;
            }
        }
        lst=cur;
    }
    
    int id[N<<1];
    
    //构建完成后，id顺序为len递增（逆拓扑序）【仅可排一次】 
    void sort()
    {
        static int bucket[N<<1];
        
        memset(bucket,0,sizeof(bucket));
        for(int i=1;i<=sz;i++)
            bucket[len[i]]++;
        for(int i=1;i<=sz;i++)
            bucket[i]+=bucket[i-1];
        for(int i=1;i<=sz;i++)
            id[bucket[len[i]]--]=i;
    }
}sam;

int n,q;
char s[N];

int endpos[N<<1];
vector<pii> v[N<<1];

inline void upmax(int &dest,int val)
{
    if(val>dest)
        dest=val;
}

ll cnt[N];
vector<pii> vq[N];

int tot,label[N<<2];
vector<int> v_add[N],v_del[N];

void dfs(int x)
{
    label[++tot]=x;
    v_add[sam.len[sam.link[x]]+1].emplace_back(tot);
    v_del[sam.len[x]].emplace_back(tot);
    
    for(pii tmp: v[x])
        dfs(tmp.second);
}

pii ans[N];

int main()
{
    scanf("%s",s+1);
    n=strlen(s+1);
    for(int l=1,r=n;l<=r;l++,r--)
        swap(s[l],s[r]);
    
    for(int i=1;i<=n;i++)
        sam.extend(s[i]-'a');
    sam.sort();
    
    for(int i=1,cur=0;i<=n;i++)
    {
        cur=sam.nxt[cur][s[i]-'a'];
        endpos[cur]=i;
    }
    for(int i=sam.sz;i>=1;i--)
    {
        int id=sam.id[i];
        cnt[sam.len[sam.link[id]]+1]++;
        cnt[sam.len[id]+1]--;
        
        upmax(endpos[sam.link[id]],endpos[id]);
    }
    for(int i=1;i<=n;i++)
        cnt[i]+=cnt[i-1];
    for(int i=2;i<=n;i++)
        cnt[i]+=cnt[i-1];
    
    for(int i=1;i<=sam.sz;i++)
    {
        int pos=endpos[i]-sam.len[sam.link[i]];
        v[sam.link[i]].emplace_back(pii(s[pos]-'a',i));
    }
    for(int i=0;i<=sam.sz;i++)
        sort(v[i].begin(),v[i].end());
    
    dfs(0);
    
    scanf("%d",&q);
    for(int i=1;i<=q;i++)
    {
        ll x;
        scanf("%lld",&x);
        
        if(x>cnt[n])
            ans[i]=pii(-1,-1);
        else
        {
            int dep=lower_bound(cnt+1,cnt+n+1,x)-cnt;
            int rnk=x-cnt[dep-1];
            vq[dep].emplace_back(pii(rnk,i));
        }
    }
    
    for(int i=1;i<=n;i++)
    {
        for(int x: v_add[i])
            add(x,1);
        
        for(pii tmp: vq[i])
        {
            int rnk=tmp.first,id=tmp.second;
            
            int cur=label[kth(rnk)];
            int L=endpos[cur]-i+1,R=endpos[cur];
            ans[id]=pii(n-R+1,n-L+1);
        }
        
        for(int x: v_del[i])
            add(x,-1);
    }
    
    for(int i=1;i<=q;i++)
        printf("%d %d\n",ans[i].first,ans[i].second);
    return 0;
}

 

有一说一，感觉很难遇到典中典的后缀树题目（有时候甚至不用往后缀树考虑就能用后缀树组切了），所以暂时就不多补充例题，遇到再议。