Splay
之前一直没学
不过这个假期必须抓紧时间搞完了
然后就是LCT
个人模板:
由于经典平衡树完全可以用pbds代替,并且与序列操作的Splay不兼容,故只保留序列操作的Splay

int a[N]; struct Splay { int root,tot; int ch[N][2]; int val[N],mn[N]; int fa[N],sz[N],rev[N],tag[N]; Splay() { root=tot=0; mn[0]=INF; } //向上更新sz,cnt void pushup(int x) { int l=ch[x][0],r=ch[x][1]; sz[x]=sz[l]+sz[r]+1; mn[x]=min(min(mn[l],mn[r]),val[x]); } //将翻转的tag向下转移 void pushdown(int x) { if(!x) return; int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); rev[l]^=1,rev[r]^=1; rev[x]=0; } if(tag[x]) { val[x]+=tag[x]; mn[x]+=tag[x]; tag[l]+=tag[x]; tag[r]+=tag[x]; tag[x]=0; } } //单旋 void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); if(ff) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } //旋转直至fa[x]==to void splay(int x,int to=0) { while(fa[x]!=to) { int f=fa[x],ff=fa[f]; if(ff!=to) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } if(!to) root=x; } //将在序列中位置为[l+1,r-1]分离出来 int split(int l,int r) { int u=kth(l),v=kth(r); splay(u),splay(v,u); return v; } //插入一段长度为n的区间到x后 void insert(int x,int n) { int v=split(x,x+1); build(ch[v][0],1,n,v); pushup(v),pushup(fa[v]); } //建立新节点 void newnode(int &x,int v,int f) { x=++tot; val[x]=v,fa[x]=f; ch[x][0]=ch[x][1]=rev[x]=tag[x]=0; } //根据数组建立一个子树 void build(int &x,int l,int r,int f) { if(l>r) return; int mid=(l+r)>>1; newnode(x,a[mid],f); build(ch[x][0],l,mid-1,x); build(ch[x][1],mid+1,r,x); pushup(x); } //删除区间[l,r] void erase(int l,int r) { int v=split(l,r+2); ch[v][0]=0; pushup(v),pushup(fa[v]); } //返回第k大元素的下标 int kth(int x) { int k=root,l=ch[k][0],r=ch[k][1]; pushdown(l),pushdown(r); while(sz[l]>=x || sz[l]+1<x) { if(sz[l]>=x) k=l; else x-=(sz[l]+1),k=r; l=ch[k][0],r=ch[k][1]; pushdown(l),pushdown(r); } return k; } //将[l,r]区间向后滚动w void roll(int l,int r,int w) { if(!w) return; int v=split(r-w+1,r+2); int tmp=ch[v][0]; fa[tmp]=ch[v][0]=0; pushup(v),pushup(fa[v]); v=split(l,l+1); fa[tmp]=v,ch[v][0]=tmp; pushdown(tmp),pushup(v),pushup(fa[v]); } //将[l,r]区间翻转 void flip(int l,int r) { int v=split(l,r+2); rev[ch[v][0]]^=1; pushdown(ch[v][0]); pushup(v),pushup(fa[v]); } //将[l,r]区间增加w void modify(int l,int r,int w) { int v=split(l,r+2); tag[ch[v][0]]=w; pushdown(ch[v][0]); pushup(v),pushup(fa[v]); } //查询[l,r]最小值 int query(int l,int r) { int v=split(l,r+2); pushup(v),pushup(fa[v]); return mn[ch[v][0]]; } //遍历序列 void trav(int x) { if(!x) return; pushdown(x); trav(ch[x][0]); if(x>0) printf("%d ",val[x]); trav(ch[x][1]); } };
UPD:除了维护序列以外,Splay还可以动态维护简单环/链,新增一个模板(只是在序列操作的基础上稍微加点东西)

//【注意】想要使用某个head/mn时,需要先splay到根 //这个板子处理的是简单环拆成链、支持循环移动的问题 //如果仅需要处理链,则无须roll,其余地方也需要稍微修改一下 //除了经典splay操作的fa,sz,rev外,其余东西需要自行init和pushup struct Splay { int ch[N][2]; int head[N]; int fa[N],sz[N],rev[N]; //T特大时会寄,需要小心 void init() { sz[0]=0; memset(ch,0,sizeof(ch)); memset(fa,0,sizeof(fa)); memset(rev,0,sizeof(rev)); } //向上更新sz,head等信息 void pushup(int x) { int l=ch[x][0],r=ch[x][1]; sz[x]=sz[l]+sz[r]+1; head[x]=l?head[l]:x; } //将翻转的tag向下转移 void pushdown(int x) { if(!x) return; int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); rev[l]^=1,rev[r]^=1; rev[x]=0; } } //单旋 void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); if(ff) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } //旋转直至fa[x]==to void splay(int x,int to=0) { while(fa[x]!=to) { int f=fa[x],ff=fa[f]; if(ff!=to) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } } //返回x所在链第k大元素的下标 int kth(int x,int k) { splay(x); int l=ch[x][0],r=ch[x][1]; pushdown(l),pushdown(r); while(sz[l]+1!=k) { if(sz[l]>=k) x=l; else k-=(sz[l]+1),x=r; l=ch[x][0],r=ch[x][1]; pushdown(l),pushdown(r); } return x; } //将链循环右移,使得x为链尾 void roll(int x) { splay(x); if(head[x]!=x) splay(head[x],x); if(!ch[x][0]) ch[x][0]=ch[x][1]; else { ch[head[x]][0]=ch[x][1]; if(ch[x][1]) { fa[ch[x][1]]=head[x]; pushup(head[x]); } } ch[x][1]=0; pushup(x); } //查x所在的链头 int findroot(int x) { while(fa[x]) x=fa[x]; return x; } //将x,y所在的链分裂,规则为分别截出(nxt[x])->y,(nxt[y])->x void split(int x,int y) { roll(x); splay(y,x); //undo contribution of x ch[x][0]=ch[y][1]; if(ch[y][1]) fa[ch[y][1]]=x,ch[y][1]=0; fa[y]=0; pushup(x),pushup(y); //calc contribution of new x, y } //将x,y所在的链合并,规则为x->(nxt[y]) void merge(int x,int y) { roll(x),roll(y); //undo contribution of x, y ch[x][1]=y,fa[y]=x; pushup(x); //calc contribution of new x } };
简易目录:
Splay是一种平衡树,能够比较方便的完成传统平衡树的各种操作(插入/删除,求rank,求第$k$大,求前驱后继)
不过在更多情况下,由于其旋转的方式比较特殊,能够方便地维护序列(能够实现区间加,区间反转,区间移动)
作为一种依赖旋转来保持平衡的平衡树,Splay的核心就是两种旋转操作
1. rotate(x):将$x$向上一层旋转
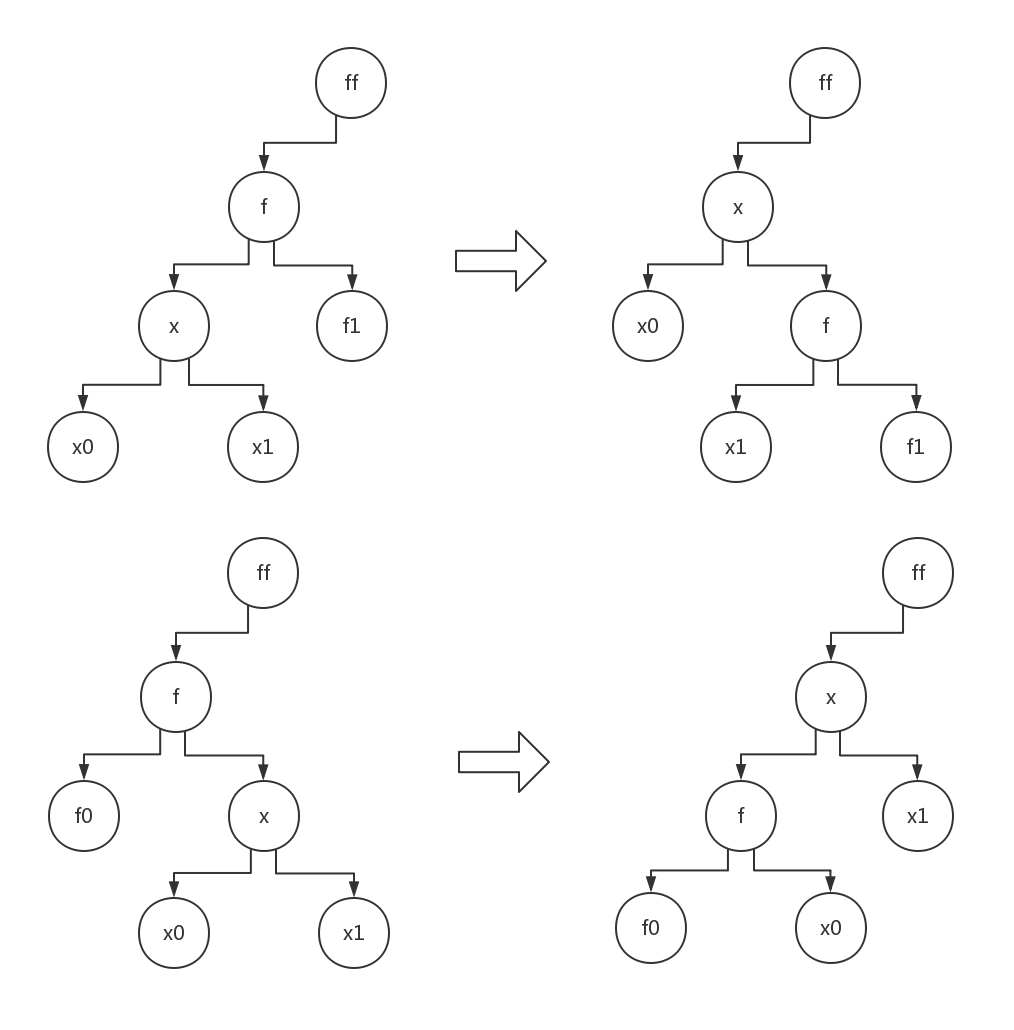
我们规定$ch[i][0]$为$i$节点的左儿子,$ch[i][1]$右儿子
那么观察上面的两种情况,能够发现一次rotate仅产生了很少的改变
记在旋转前,$x$是$f$在$dir$方向的儿子($0$为左,$1$为右),那么可以这样概括:
$ch[f][dir]=ch[x][dir\text{^}1]$:即$f$在$dir$方向的儿子由$x$变为$ch[x][dir\text{^}1]$
$ch[x][dir\text{^}1]=f$:即$x$在$dir\text{^}1$方向的儿子由$ch[x][dir\text{^}1]$变为$f$
$ff$的一个儿子由$f$变为$x$
当然,对应节点的父亲也需要对应更新
于是可以这样用代码实现
void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); if(ff) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; }
2. splay(x,to):将$x$向上旋转,直至其父亲为$to$
Splay的任何经典平衡树操作,都需要将待处理点旋转至根节点(即$to=0$),那么单次操作的复杂度就与树高相关
仔细观察rotate($x$),可以发现 将某一节点旋转至根节点 并不会使树的高度减少
那么如果遇到一棵申必的树,并且一直操作叶子节点、将其rotate至根节点,那么单次操作的复杂度恒为$O(n)$,就一点都不平衡了
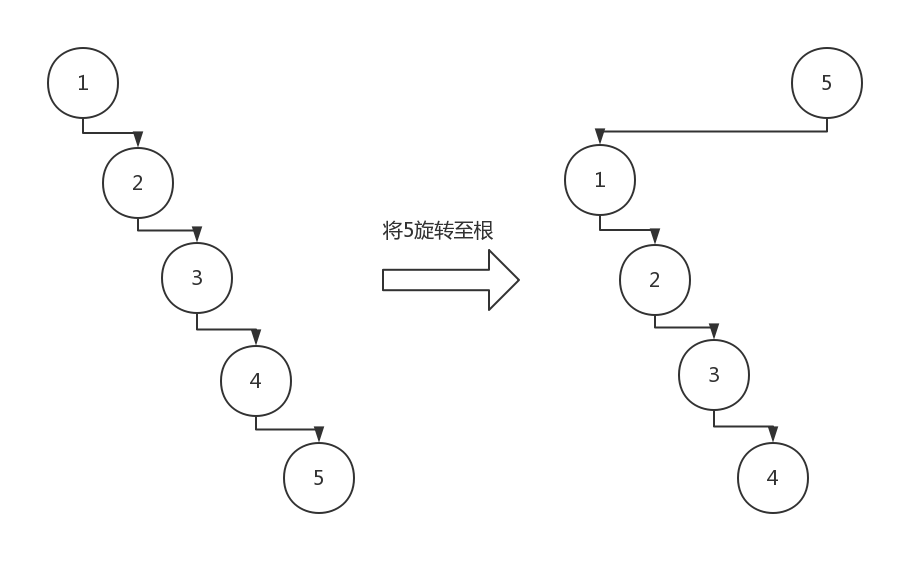
可以发现,如果将$x$旋转至根的过程中,$x$将走过一段很长的、同方向的链,那么下一次操作该链的底端节点时仍将走过这样长的一段路程,使得单次复杂度退化成$O(n)$
而splay函数所做的事情,就是将这样的一条链进行“折叠”
折叠的标准是这样的:若$x,f,ff$在一条直线上,那么先rotate($f$),再rotate($x$);否则两次rotate($x$)
void splay(int x,int to=0) { while(fa[x]!=to) { int f=fa[x],ff=fa[f]; if(ff!=to) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } if(!to) root=x; }
两次rotate($x$)的情况就是$x,f,ff$呈现出“之”字形,那么没有折叠的必要
而降低均摊复杂度的关键就在于先rotate($f$)、再rotate($x$)的情况,如下所示

从感性的角度来看,这样的一次splay将长链折叠为原来长度的一半,那么在多次折叠之后,树的深度不会特别大;严格的证明听说要用上势能分析
我们可以简单地认为,在多次splay之后,树的深度是$logn$级别的
在以后的所有操作中,可以考虑多多splay,以防止平衡树退化
记$val[i]$表示,编号为$i$的点所代表的值
为了处理各种操作,我们需要额外维护一些信息
$cnt[i]$表示,值为$val[i]$的元素一共出现多少次
$sz[i]$表示,以$i$为根的子树的大小
这些值都是十分容易维护的,只需要在rotate的过程中向上更新即可
void pushup(int x) { sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x]; } void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); if(ff) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x);//这是新加的语句 }
1. find(x):返回值为$x$的节点编号
会BST应该都知道做法
从$root$出发,若对于当前点$k$有$val[k]<x$就向左走,$val[k]>x$就向右走,$val[k]=x$就停下
int find(int x) { int k=root; while(val[k]!=x) k=ch[k][x>val[k]]; return k; }
其实该函数仅会在delete($x$)中用到,不过出于由易到难的考虑,将其放在最前面
2. insert(x):插入一个值为$x$的元素
首先,我们需要定位到待插入的位置;类似find函数,不过需要额外记录$k$的父亲$f$,以方便将新节点连到树上
若之前未插入过$x$,那么最后$k$会走到一个空节点,新建节点、并将其连到树上即可
若之前插入过$x$,那么最后$k$会走到一个树上节点,直接$cnt[k]++$
记得在最后splay($k$)
void insert(int x) { int f=0,k=root; while(k && val[k]!=x) f=k,k=ch[k][x>val[k]]; if(k) ++cnt[k]; else { k=++tot; if(!f) root=k; else ch[f][x>val[f]]=k; val[k]=x,cnt[k]=sz[k]=1,fa[k]=f; } splay(k); }
3. kth(x):返回第$x$小节点的编号(从小到大第$x$)
寻找第$x$小节点,需要从$root$出发,对于当前结点$k$判断是向左/右儿子走、或是$k$即为第$x$小
若$sz[ch[k][0]]\geq x$,即左子树大小大于$x$,那么第$x$小节点必在$k$的左子树中,向左儿子走
若$sz[ch[k][0]]<x$且$sz[ch[k][0]]+cnt[k]\geq x$,即第$x$小节点为$k$,返回即可
若$sz[ch[k][0]]+cnt[k]<x$,即第$x$小节点必在$k$的右子树中,向右儿子走(走到右儿子之前,需要注意对$x$减去$sz[ch[k][0]]+cnt[k]$)
那么就是这样的实现:
int kth(int x) { int k=root; while(sz[ch[k][0]]>=x || sz[ch[k][0]]+cnt[k]<x) { if(sz[ch[k][0]]>=x) k=ch[k][0]; else x-=(sz[ch[k][0]]+cnt[k]),k=ch[k][1]; } return k; }
这个函数在序列操作中十分重要,承担着下传各种标记的任务(到时候就需要在此基础上pushdown了)
4. pre(x), suc(x):返回$x$前驱/后继的编号,不存在则返回$0$
由于两者是对称的,仅说一下pre($x$)
从$root$出发,若当前节点$k$的值$val[k]>=x$,则向左儿子走;否则更新答案,并且向右儿子走
这样一定能找到$x$的前驱,因为上述走法是在不停地找值小于$x$、并且值尽可能大的节点
int pre(int x) { int k=root,ans=0; while(k) if(val[k]>=x) k=ch[k][0]; else ans=k,k=ch[k][1]; return ans; } int suc(int x) { int k=root,ans=0; while(k) if(val[k]<=x) k=ch[k][1]; else ans=k,k=ch[k][0]; return ans; }
5. erase(x):删除值为$x$的元素(若有多个仅删除一个)
通过erase($x$),我们能够初步了解Splay的精髓,就是两端逼近
首先处理特殊情况,就是$x$为平衡树中最小/最大/唯一元素:条件为前驱、后继中至少有一个为$0$
先通过find函数确定其位置$k$,然后splay($k$)将其移到根
由于其为最小/最大元素,那么$k$的左右儿子中至少有一个为空;于是将$k$的非空儿子作为根即可
需要特判一下删空平衡树的情况
然后考虑处理一般的情况:此时前驱后继均存在,分别记为$prex,sucx$
先splay($prex$)将其旋转至根;由于$val[prex]<val[sucx]$,此时$sucx$必在$prex$的右子树中
再splay($sucx$, $prex$)将后继旋转至$prex$的右儿子
此时考虑$sucx$的左子树内的情况:其中的节点$y$必定满足$val[prex]<val[y]<val[sucx]$,而满足这个条件的节点仅有值为$x$的
于是我们成功地将值为$x$的节点限制在了一个确定的位置,即$ch[sucx][0]$;令$ch[sucx][0]=0$就能删除节点
void erase(int x) { int prex=pre(x),sucx=suc(x); if(!prex || !sucx) { int k=find(x); cnt[k]--; splay(k); if(!cnt[k]) { int dir=ch[k][1]>0; root=ch[k][dir]; fa[root]=0; } } else { splay(prex); splay(sucx,prex); int k=ch[sucx][0]; cnt[k]--; if(!cnt[k]) ch[sucx][0]=0; pushup(sucx),pushup(prex); } }
这样两端逼近的思路将广泛用于序列操作中
同时,为了解决没有前驱/后继的特殊情况,在序列操作时往往会向空树中插入两个虚拟节点作为头和尾
经典例题1:BZOJ 3224 (Tyvj 1728 普通平衡树)
需要实现所有平衡树的经典操作
上面的函数就是根据这道题目的要求来的
求rank由于跟求第$k$小差不多、且在序列操作中用不到,就没有列在上面了

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=100005; int n,tot; int root,ch[N][2]; int val[N],fa[N],cnt[N],sz[N]; inline void pushup(int x) { sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x]; } inline void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); if(ff) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } inline int find(int x) { int k=root; while(val[k]!=x && ch[k][x>val[k]]) k=ch[k][x>val[k]]; return k; } inline void splay(int x,int to=0) { while(fa[x]!=to) { int f=fa[x],ff=fa[f]; if(ff!=to) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } if(!to) root=x; } inline void insert(int x) { int f=0,k=root; while(k && val[k]!=x) { f=k; k=ch[k][x>val[k]]; } if(k) ++cnt[k]; else { k=++tot; if(!f) root=k; else ch[f][x>val[f]]=k; val[k]=x,cnt[k]=sz[k]=1,fa[k]=f; } splay(k); } inline int rank(int x) { int k=root,ans=0; while(k && val[k]!=x) if(val[k]>x) k=ch[k][0]; else ans+=sz[ch[k][0]]+cnt[k],k=ch[k][1]; ans+=sz[ch[k][0]]+1; return ans; } inline int kth(int x) { int k=root; while(sz[ch[k][0]]>=x || sz[ch[k][0]]+cnt[k]<x) if(sz[ch[k][0]]>=x) k=ch[k][0]; else x-=(sz[ch[k][0]]+cnt[k]),k=ch[k][1]; return k; } inline int pre(int x) { int k=root,ans=0; while(k) if(val[k]>=x) k=ch[k][0]; else ans=k,k=ch[k][1]; return ans; } inline int suc(int x) { int k=root,ans=0; while(k) if(val[k]<=x) k=ch[k][1]; else ans=k,k=ch[k][0]; return ans; } inline void erase(int x) { int prex=pre(x),sucx=suc(x); if(!prex || !sucx) { int k=find(x); cnt[k]--; splay(k); if(!cnt[k]) { int dir=ch[k][1]>0; root=ch[k][dir]; fa[root]=0; } } else { splay(prex); splay(sucx,prex); int k=ch[sucx][0]; cnt[k]--; if(!cnt[k]) ch[sucx][0]=0; pushup(sucx),pushup(prex); } } int main() { int n; scanf("%d",&n); while(n--) { int opt,x; scanf("%d%d",&opt,&x); if(opt==1) insert(x); if(opt==2) erase(x); if(opt==3) printf("%d\n",rank(x)); if(opt==4) printf("%d\n",val[kth(x)]); if(opt==5) printf("%d\n",val[pre(x)]); if(opt==6) printf("%d\n",val[suc(x)]); } return 0; }
Splay最强悍的地方就在于能够进行各种序列操作,并在序列操作的同时维护区间信息
注意:对于用于序列操作的Splay,其$val[i]$是不满足BST性质的
同时,$val[kth(i)]$是序列中的第$i$个元素$a_i$
故可以这样理解,在进行序列操作时,Splay所真正维护的是各元素的rank
而完成区间操作的资本就是在erase($x$)中所说的两端逼近
假设我们想对一段区间$[l,r]$进行操作,可以用类似的方法将处于该区间内的元素夹在一确定位置:
先splay(kth($l-1$)),即将$a_{l-1}$旋转到$root$;此时$a_{r+1}$的rank更大,所以处于$a_{l-1}$的右子树中
再splay(kth($r+1$), kth($l-1$)),即将$a_{r+1}$旋转至$a_{l-1}$的右儿子
此时$a_l,a_{l+1},...,a_{r-1},a_r$均处在$a_{r+1}$的左子树中,可以方便地进行查询或者操作
int split(int l,int r) { int u=kth(l),v=kth(r); splay(u),splay(v,u); return v; }
由于我们在夹出区间的过程中需要用到$a_0,a_{n+1}$,那么不妨在空树中插入两个节点作为头和尾
于是所有元素的rank就变成了$1,2,...,n,n+1,n+2$
所以夹出区间$[l,r]$调用的是split($l$,$r+2$)
1. erase(l, r):删除区间$[l,r]$间的元素
将区间夹出来后删掉即可
void erase(int l,int r) { int v=split(l,r+2); ch[v][0]=0; pushup(v),pushup(fa[v]); }
2. insert(x, n):插入一段长度为$n$的序列到$x$后($x$指的是包含头尾节点的rank)
先夹出待插入的位置(应该为一空节点),然后采用分治$O(n)$地对于新增序列建树,最后将新建树的根节点放到待插入位置
void newnode(int &x,int v,int f) { x=++tot; val[x]=v,fa[x]=f; ch[x][0]=ch[x][1]=rev[x]=tag[x]=0; } void build(int &x,int l,int r,int f) { if(l>r) return; int mid=(l+r)>>1; newnode(x,a[mid],f); build(ch[x][0],l,mid-1,x); build(ch[x][1],mid+1,r,x); pushup(x); } void insert(int x,int n) { int v=split(x,x+1); build(ch[v][0],1,n,v); pushup(v),pushup(fa[v]); }
3. 区间移动
那就是1+2,即先用类似erase($l$, $r$)的方法夹出区间$[l,r]$对应的子树并截下来,然后用类似insert($x$, $n$)将其接到需要的位置
4. 区间打懒标记
将需要打标记的区间夹出来后,将标记打在子树的根节点上
仅仅打出标记不算本事,真正难的在于如何有序、充分地将打过的标记下传
我们以 区间翻转 和 区间加 为例
1. 区间翻转(仅需要pushdown的标记)
经典例题2:BZOJ 3223 (Tyvj 1729 文艺平衡树)
假设我们已经将待处理区间夹出来了,并在该子树的根节点打上了翻转标记,那么如何将其下传?
我们先考虑一下翻转标记的意义:
它表示,该子树中的所有节点都需要交换左右儿子
道理很简单,将区间中rank比它大的放到它的左边,rank比它小的放到右边,那么就相当于将当前点放到了正确的位置上;如果对于子树中的所有点都这样操作,整个区间就被翻转了
同时,对一个子树翻转多次可以简单地规约到翻转$0$次/$1$次,因为等价于对每个节点交换多少次左右儿子
于是,只处理区间翻转标记的pushdown函数就可以写出来了
void pushdown(int x) { if(tag[x]) { swap(ch[x][0],ch[x][1]); tag[ch[x][0]]^=1; tag[ch[x][1]]^=1; tag[x]=0; } }
打上标记的办法如上所说,很简单
void flip(int l,int r) { int v=split(l,r+2); if(ch[v][0]) tag[ch[v][0]]^=1; }
由于我们仅仅需要处理区间翻转,所以只需要维护$sz[i],cnt[i]$,而这些东西在交换左右儿子时并不会改变,所以无需修改pushup函数
然后考虑一下在什么地方需要将标记下传
仔细分析一下,其实我们一共就用到了几个函数:rotate,splay,kth,split,flip
其中,splay和rotate都是向上旋转的过程;假设$x$的父亲节点$f$曾经存在过标记,那么也应当在定位到$x$的时候下传过了,所以在这两个函数中无需下传
flip是打标记的函数,真正调用的是split
split调用了两次kth和两次splay,其中splay已经确认过无需下传了,那么唯一需要下传标记的就是定位区间的kth函数
由于在kth函数中需要知道左子树的大小,所以在比较当前节点之前就需要将翻转标记下传
int kth(int x) { int k=root; pushdown(k); while(sz[ch[k][0]]>=x || sz[ch[k][0]]+cnt[k]<x) { if(sz[ch[k][0]]>=x) k=ch[k][0]; else x-=(sz[ch[k][0]]+cnt[k]),k=ch[k][1]; pushdown(k); } return k; }
2. 区间加(不仅需要pushdown,还需要pushup)
一般在有区间加的要求时,需要查询的是 区间最大值/区间最小值/区间和
那么类似线段树懒标记,在操作过后是需要pushup的,即用左右儿子的信息更新当前节点的信息
以区间最小值为例,我们就需要维护 以每个节点为根的子树中 的最小值$mn[i]$
pushdown依然是很好写的(这里的pushdown函数仅针对区间加标记)
void pushdown(int x) { if(!x) reuturn; if(tag[x]) { val[x]+=tag[x]; mn[x]+=tag[x]; tag[l]+=tag[x]; tag[r]+=tag[x]; tag[x]=0; } }
pushup也很显然,仅需要在维护$sz[i],cnt[i]$的基础上多维护下$mn[i]$即可(在维护序列时,$cnt[i]=1$,故可以省去)
void pushup(int x) { int l=ch[x][0],r=ch[x][1]; sz[x]=sz[l]+sz[r]+1; mn[x]=min(min(mn[l],mn[r]),val[x]); }
不过这里需要注意要将$mn[0]$提前赋为$INF$,否则会在pushup时产生错误(当某个节点的左右儿子中有空节点时)
我们需要考虑一下pushup的条件:由于需要利用左右儿子的信息更新当前节点,所以左右儿子需要保证已经提前被pushdown
对比一下之前的区间翻转:若只需要处理区间翻转,那么在kth的过程中只需要保证当前点被pushdown即可
两者之间的区别导致kth函数略有不同
int kth(int x) { int k=root,l=ch[k][0],r=ch[k][1]; pushdown(l),pushdown(r); while(sz[l]>=x || sz[l]+1<x) { if(sz[l]>=x) k=l; else x-=(sz[l]+1),k=r; l=ch[k][0],r=ch[k][1]; pushdown(l),pushdown(r); } return k; }
由于区间加标记对pushdown的要求比区间翻转标记的高,所以在模板中的pushdown函数遵从 区间加标记 的标准
跟线段树中的区间加一样,在给定位到的节点打上区间加标记时 需要立即将当前节点pushdown,否则在向上旋转时无法将这次的修改更新上去
同时在所有调用过split函数的地方,都需要额外pushup两次
以erase($l$, $r$)为例:
void erase(int l,int r) { int v=split(l,r+2); ch[v][0]=0; pushup(v),pushup(fa[v]); }
这就是标记下传的全部内容了,关键还是注意不同标记对pushdown的要求不同
根据个人感觉从易到难排序
1. BZOJ 1269 (文本编辑器editor,$AHOI2006$)
这题中的“光标”就相当于序列操作的左端点$l$
注意一下数据中有三个问题:
(1) $n$没有实际用处,因为有几组数据中操作数不等于$n$;用while读入
(2) 数据存在插入换行符'\n'的情况(虽然题面中说没有),并且可能会将其输出;当输出字符为换行符时,直接换行就行了,不用输出两次'\n'
(3) 数据存在删除的右端点$r$超过序列长度,所以在空树时需要插入$4$个虚拟节点

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=3000005; char a[N]; struct Splay { int root,tot; int ch[N][2]; int val[N],fa[N],cnt[N],sz[N],tag[N]; Splay() { root=tot=0; memset(ch,0,sizeof(ch)); memset(val,0,sizeof(val)); memset(fa,0,sizeof(fa)); memset(cnt,0,sizeof(cnt)); memset(sz,0,sizeof(sz)); memset(tag,0,sizeof(tag)); } //向上更新sz,cnt void pushup(int x) { sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x]; } //将翻转的tag向下转移(此时splay无序) void pushdown(int x) { if(tag[x]) { swap(ch[x][0],ch[x][1]); tag[ch[x][0]]^=1; tag[ch[x][1]]^=1; tag[x]=0; } } //单旋 void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); if(ff) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } //旋转直至fa[x]==to void splay(int x,int to=0) { while(fa[x]!=to) { int f=fa[x],ff=fa[f]; if(ff!=to) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } if(!to) root=x; } //建立新节点 void newnode(int &x,int v,int f) { x=++tot; val[x]=v,cnt[x]=sz[x]=1,fa[x]=f; } //根据数组 建立一个子树(一般在无序时调用) void build(int &x,int l,int r,int f) { if(l>r) return; int mid=(l+r)>>1; newnode(x,a[mid],f);//a需要定义在Splay前 build(ch[x][0],l,mid-1,x); build(ch[x][1],mid+1,r,x); pushup(x); } //返回第k大元素的下标 int kth(int x) { int k=root; pushdown(k); while(sz[ch[k][0]]>=x || sz[ch[k][0]]+cnt[k]<x) { if(sz[ch[k][0]]>=x) k=ch[k][0]; else x-=(sz[ch[k][0]]+cnt[k]),k=ch[k][1]; pushdown(k); } return k; } //将[l,r]区间翻转(此时splay无序) //从0插入到n+1 void flip(int l,int r) { l=kth(l),r=kth(r+2); splay(l); splay(r,l); if(ch[r][0]) tag[ch[r][0]]^=1; } }t; int n,m,cursor=1; char opt[N]; void Insert() { int u=t.kth(cursor); t.splay(u); int v=t.kth(cursor+1); t.splay(v,u); int tmp; t.build(tmp,1,m,0); t.ch[v][0]=tmp; t.fa[tmp]=v; t.pushup(v),t.pushup(u); } void Move() { cursor=m+1; } void Delete() { int u=t.kth(cursor); t.splay(u); int v=t.kth(cursor+m+1); t.splay(v,u); t.ch[v][0]=0; t.pushup(v),t.pushup(u); } void Rotate() { int u=t.kth(cursor); t.splay(u); int v=t.kth(cursor+m+1); t.splay(v,u); t.tag[t.ch[v][0]]^=1; } void Get() { int u=t.kth(cursor+1); t.splay(u); if(t.val[u]!='\n') putchar(t.val[u]); putchar('\n'); } void Prev() { cursor--; } void Next() { cursor++; } int main() { scanf("%d",&n); t.build(t.root,1,4,0); while(~scanf("%s",opt+1)) { if(opt[1]=='I') { scanf("%d",&m),getchar(); for(int i=1;i<=m;i++) a[i]=getchar(); Insert(); } if(opt[1]=='M') scanf("%d",&m),Move(); if(opt[1]=='D') scanf("%d",&m),Delete(); if(opt[1]=='R') scanf("%d",&m),Rotate(); if(opt[1]=='G') Get(); if(opt[1]=='P') Prev(); if(opt[1]=='N') Next(); } return 0; }
2. POJ 3580 ($Super\ Memo$)
这题中唯一非传统的操作是REVOLVE,即将区间循环右移
不过这可以通过区间移动(拼接)实现,将循环右移至开头的那段元素截取出来,然后拼到开头的位置

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=200005; const int INF=1<<30; int a[N]; struct Splay { int root,tot; int ch[N][2]; int val[N],mn[N]; int fa[N],sz[N],rev[N],tag[N]; Splay() { root=tot=0; mn[0]=INF; } //向上更新sz,cnt void pushup(int x) { int l=ch[x][0],r=ch[x][1]; sz[x]=sz[l]+sz[r]+1; mn[x]=min(min(mn[l],mn[r]),val[x]); } //将翻转的tag向下转移(此时splay无序) void pushdown(int x) { if(!x) return; int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); rev[l]^=1,rev[r]^=1; rev[x]=0; } if(tag[x]) { val[x]+=tag[x]; mn[x]+=tag[x]; tag[l]+=tag[x]; tag[r]+=tag[x]; tag[x]=0; } } //单旋 void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); if(ff) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } //旋转直至fa[x]==to void splay(int x,int to=0) { while(fa[x]!=to) { int f=fa[x],ff=fa[f]; if(ff!=to) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } if(!to) root=x; } //将在序列中位置为[l+1,r-1]分离出来 int split(int l,int r) { int u=kth(l),v=kth(r); splay(u),splay(v,u); return v; } //插入一段长度为n的区间到x后(一般无序) void insert(int x,int n) { int v=split(x,x+1); build(ch[v][0],1,n,v); pushup(v),pushup(fa[v]); } //建立新节点 void newnode(int &x,int v,int f) { x=++tot; val[x]=v,fa[x]=f; ch[x][0]=ch[x][1]=rev[x]=tag[x]=0; } //根据数组 建立一个子树(一般在无序时调用) void build(int &x,int l,int r,int f) { if(l>r) return; int mid=(l+r)>>1; newnode(x,a[mid],f); build(ch[x][0],l,mid-1,x); build(ch[x][1],mid+1,r,x); pushup(x); } //删除区间[l,r](一般无序) void erase(int l,int r) { int v=split(l,r+2); ch[v][0]=0; pushup(v),pushup(fa[v]); } //返回第k大元素的下标 int kth(int x) { int k=root,l=ch[k][0],r=ch[k][1]; pushdown(l),pushdown(r); while(sz[l]>=x || sz[l]+1<x) { if(sz[l]>=x) k=l; else x-=(sz[l]+1),k=r; l=ch[k][0],r=ch[k][1]; pushdown(l),pushdown(r); } return k; } //将[l,r]区间向后滚动w(此时splay无序) void roll(int l,int r,int w) { if(!w) return; int v=split(r-w+1,r+2); int tmp=ch[v][0]; fa[tmp]=ch[v][0]=0; pushup(v),pushup(fa[v]); v=split(l,l+1); fa[tmp]=v,ch[v][0]=tmp; pushdown(tmp),pushup(v),pushup(fa[v]); } //将[l,r]区间翻转(此时splay无序) void flip(int l,int r) { int v=split(l,r+2); rev[ch[v][0]]^=1; pushdown(ch[v][0]); pushup(v),pushup(fa[v]); } //将[l,r]区间增加w(此时splay无序) void modify(int l,int r,int w) { int v=split(l,r+2); tag[ch[v][0]]=w; pushdown(ch[v][0]); pushup(v),pushup(fa[v]); } //查询[l,r]最小值 int query(int l,int r) { int v=split(l,r+2); pushup(v),pushup(fa[v]); return mn[ch[v][0]]; } }t; int n,m; char opt[20]; int main() { a[1]=a[2]=INF; t.build(t.root,1,2,0); scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); t.insert(1,n); scanf("%d",&m); while(m--) { scanf("%s",opt+1); int x,y,w; if(opt[1]=='A') { scanf("%d%d%d",&x,&y,&w); t.modify(x,y,w); } if(opt[1]=='R' && opt[4]=='E') { scanf("%d%d",&x,&y); t.flip(x,y); } if(opt[1]=='R' && opt[4]=='O') { scanf("%d%d%d",&x,&y,&w); w%=(y-x+1); t.roll(x,y,w); } if(opt[1]=='I') { scanf("%d%d",&x,&a[1]); t.insert(x+1,1); } if(opt[1]=='D') { scanf("%d",&x); t.erase(x,x); } if(opt[1]=='M') { scanf("%d%d",&x,&y); printf("%d\n",t.query(x,y)); } } return 0; }
3. Luogu P2042 (维护数列,$NOI2005$)
这题中困难的是维护最大子列,不过我们可以类比线段树中的维护最大子段和
对于以$i$为根的子树所对应的区间
用$lx[i]$表示从左端点开始选的最大子段和,$rx[i]$表示从右端点开始选的,$mx[i]$表示当前区间的最大子段和
那么用左儿子$l$、右儿子$r$更新当前节点的$x$可以这样表示
$lx[x]=max(lx[l],sum[l]+val[x]+lx[r])$,即要不就用左子区间的$lx$,要不就全选左子区间,然后拼上右子区间的$lx$;$rx[x]$是对称的
$mx[x]=max(mx[l],mx[r],rx[l]+val[x]+lx[r])$,即要不是左或右子区间的最大子段和,要不用左子区间的$rx$拼上右子区间的$lx$
然后在此题中要注意内存回收,删除的时候用一个队列收集所有可用的编号就可以了

#include <cstdio> #include <cstring> #include <stdexcept> #include <algorithm> using namespace std; inline void read(int &x) { int ch=getchar(),op=1; while(ch!='-' && (ch<'0' || ch>'9')) ch=getchar(); if(ch=='-') op=-1,ch=getchar(); x=0; while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar(); x*=op; } const int N=500005; const int INF=1<<30; int a[N]; int q[N],head=0,rear=1; inline int nextpos() { if(++head==N) head=3; return q[head]; } inline void recycle(int pos) { q[rear]=pos; if(++rear==N) rear=3; } struct Splay { int root,tot; int ch[N][2]; int val[N],fa[N],sz[N],sum[N]; int tag[N],rev[N]; int lx[N],rx[N],mx[N]; Splay() { root=0; lx[0]=rx[0]=0,mx[0]=-INF; } //向上更新sz,cnt void pushup(int x) { int l=ch[x][0],r=ch[x][1]; sz[x]=sz[l]+sz[r]+1; sum[x]=sum[l]+sum[r]+val[x]; lx[x]=max(lx[l],sum[l]+val[x]+lx[r]); rx[x]=max(rx[r],sum[r]+val[x]+rx[l]); mx[x]=max(max(mx[l],mx[r]),rx[l]+val[x]+lx[r]); } //将翻转的tag向下转移(此时splay无序) void pushdown(int x) { if(!x) return; int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); swap(lx[x],rx[x]); rev[l]^=1,rev[r]^=1; rev[x]=0; } if(tag[x]) { sum[x]=sz[x]*val[x]; lx[x]=rx[x]=max(0,sum[x]); mx[x]=max(val[x],sum[x]); tag[l]=tag[r]=1; val[l]=val[r]=val[x]; tag[x]=0; } } //单旋 void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); if(ff) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } //旋转直至fa[x]==to void splay(int x,int to=0) { while(fa[x]!=to) { int f=fa[x],ff=fa[f]; if(ff!=to) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } if(!to) root=x; } //将在序列中位置为[l+1,r-1]分离出来 int split(int l,int r) { int u=kth(l),v=kth(r); splay(u),splay(v,u); return v; } //插入一段长度为n的区间到x后(一般无序) void insert(int x,int n) { int v=split(x,x+1); build(ch[v][0],1,n,v); pushup(v),pushup(fa[v]); } //建立新节点 void newnode(int &x,int v,int f) { x=nextpos(); val[x]=v,fa[x]=f; ch[x][0]=ch[x][1]=rev[x]=tag[x]=0; } //根据数组 建立一个子树(一般在无序时调用) void build(int &x,int l,int r,int f) { if(l>r) return; int mid=(l+r)>>1; newnode(x,a[mid],f); build(ch[x][0],l,mid-1,x); build(ch[x][1],mid+1,r,x); pushup(x); } void collect(int x) { if(!x) return; collect(ch[x][0]); recycle(x); collect(ch[x][1]); } //删除区间[l,r](一般无序) void erase(int l,int r) { int v=split(l,r+2); collect(ch[v][0]); ch[v][0]=0; pushup(v),pushup(fa[v]); } //返回第k大元素的下标 int kth(int x) { int k=root,l=ch[k][0],r=ch[k][1]; pushdown(l),pushdown(r); while(sz[l]>=x || sz[l]+1<x) { if(sz[l]>=x) k=l; else x-=(sz[l]+1),k=r; l=ch[k][0],r=ch[k][1]; pushdown(l),pushdown(r); } return k; } //将[l,r]区间翻转(此时splay无序) void flip(int l,int r) { int v=split(l,r+2); rev[ch[v][0]]^=1; pushdown(ch[v][0]); pushup(v),pushup(fa[v]); } //将[l,r]区间刷成w(此时splay无序) void modify(int l,int r,int w) { int v=split(l,r+2); val[ch[v][0]]=w,tag[ch[v][0]]=1; pushdown(ch[v][0]); pushup(v),pushup(fa[v]); } //查询[l,r]区间和 int query(int l,int r) { int v=split(l,r+2); pushup(v),pushup(fa[v]); return sum[ch[v][0]]; } //查询最大子序列和 int maxsub() { return mx[root]; } }t; int n,m; char opt[20]; int main() { for(int i=0;i<N;i++) q[i]=i; read(n),read(m); a[1]=a[2]=-INF; t.build(t.root,1,2,0); for(int i=1;i<=n;i++) read(a[i]); t.insert(1,n); while(m--) { scanf("%s",opt+1); int pos,tot,c; if(opt[3]=='S') { read(pos),read(tot); for(int i=1;i<=tot;i++) read(a[i]); t.insert(pos+1,tot); } if(opt[3]=='L') { read(pos),read(tot); t.erase(pos,pos+tot-1); } if(opt[3]=='K') { read(pos),read(tot),read(c); t.modify(pos,pos+tot-1,c); } if(opt[3]=='V') { read(pos),read(tot); t.flip(pos,pos+tot-1); } if(opt[3]=='T') { read(pos),read(tot); printf("%d\n",t.query(pos,pos+tot-1)); } if(opt[3]=='X') printf("%d\n",t.maxsub()); } return 0; }
Splay没LCT那么高级,维护不了树的结构。但是既然能维护序列,就能维护链,同时对于简单环也可以将其拆成一个首尾相接的链来维护。
其实和序列操作比没什么特别大的修改,只是有几点区别:
1. 在维护序列时,我们只有唯一的位置有 $fa[i]=0$ (即root),因为每次操作后我们都会把切出的序列粘到合适的地方;但在维护链时,不同的链之间是不相连的,所以每条链上都有一个位置有 $fa[i]=0$(相当于每条链都是一个Splay)。
2. 根据1,我们可以维护每个链的链头head:从该链对应的root一直向左走就是整个Splay中rank最小的点。这个需要在pushup中维护,同时需要注意,假如想使用 $head[x]$ ,必须先 $splay(x)$ 将其旋转到根上才能查,因为子树中的head是信息不全的。
3. 对于维护简单环的情况,假设需要进行两个环的合并,可以将待合并的端点循环右移到链的最后(如板子中的 $roll()$ 函数),一般来说能省去很多讨论。
基本是模板题:Lexicographic Comparison (2022牛客多校 Day8 G)
首先,可以发现 swap_a 直接在 $a$ 数组上交换即可,只需要在意 swap_p 和 cmp。接着我们考虑置换 $p$ 的性质,其能够对于序列构成多个置换,每个置换为长度不一的简单环。进行一次 swap_p 时,相当于将两个简单环合并(当 $x,y$ 属于不同环)或者将一个简单环分割成两个(当 $x,y$属于相同环)。现在考虑 cmp 时第一个不相同的字符应该出现在环长不能被 $\mathrm{abs}(x-y)$ 除尽的、环中最小位置最靠前的地方。当我们找到这个环和第一个不相同的位置 $pos$ 以后,我们对 $pos$ 分别置换 $x,y$ 次(即在链上向后走 $x,y$ 次),就能知道 $A_x, A_y$ 在 $pos$ 的位置上会对应的 $a_i$。
现在考虑维护环中的最小位置 $mn$,这个可以在 Splay 中通过 pushup 简单维护:$mn[x]=\mathrm{min}\left(mn[ls],min[rs],x\right)$。接着考虑如何维护第一个不能除尽的位置,我们不妨将环长分别放在各自 $mn$ 的位置,然后求 $1$ 到 $i$ 的最小公倍数,假如这个最小公倍数不能被 $\mathrm{abs}(x,y)$ 整除就说明某个环不能进行整数次置换,则 $A_x, A_y$ 在该位置一定不相同。线段树上二分(也可以直接二分,多一个 log)找到最小的第一个不能被整除的位置 $pos$ 即可。

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef __int128 i128; const int N=100005; const int oo=1<<30; const ll MAX_VAL=1000000000LL*1000000000; int t_sz; ll t[N<<2]; inline ll merge(ll x,ll y) { if(!x || !y) return 0LL; i128 res=i128(x)*y/__gcd(x,y); return (res>MAX_VAL?0:res); } inline void pushup(int k) { if(!t[k<<1] || !t[k<<1|1]) t[k]=0; else t[k]=merge(t[k<<1],t[k<<1|1]); } inline void modify(int k,int pos,int a,int b,int x) { if(a==b) { t[k]=x; return; } int mid=(a+b)>>1; if(pos<=mid) modify(k<<1,pos,a,mid,x); else modify(k<<1|1,pos,mid+1,b,x); pushup(k); } void modify(int pos,int x) { modify(1,pos,1,t_sz,x); } inline ll query(int k,int l,int r,int a,int b) { if(a>r || b<l) return 1; if(a>=l && b<=r) return t[k]; int mid=(a+b)>>1; ll lans=query(k<<1,l,r,a,mid),rans=query(k<<1|1,l,r,mid+1,b); return merge(lans,rans); } ll query(int l,int r) { return query(1,l,r,1,t_sz); } //【注意】想要使用某个head/mn时,需要先splay到根 //这个板子处理的是简单环拆成链、支持循环移动的问题 //如果仅需要处理链,则无须roll,其余地方也需要稍微修改一下 //除了经典splay操作的fa,sz,rev外,其余东西需要自行init和pushup struct Splay { int ch[N][2]; int head[N],mn[N]; int fa[N],sz[N],rev[N]; void init() { sz[0]=0,mn[0]=oo; memset(ch,0,sizeof(ch)); memset(fa,0,sizeof(fa)); memset(rev,0,sizeof(rev)); } //向上更新sz,head等信息 void pushup(int x) { int l=ch[x][0],r=ch[x][1]; sz[x]=sz[l]+sz[r]+1; head[x]=l?head[l]:x; mn[x]=min(min(mn[l],mn[r]),x); } //将翻转的tag向下转移 void pushdown(int x) { if(!x) return; int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); rev[l]^=1,rev[r]^=1; rev[x]=0; } } //单旋 void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); if(ff) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } //旋转直至fa[x]==to void splay(int x,int to=0) { while(fa[x]!=to) { int f=fa[x],ff=fa[f]; if(ff!=to) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } } //返回x所在链第k大元素的下标 int kth(int x,int k) { splay(x); int l=ch[x][0],r=ch[x][1]; pushdown(l),pushdown(r); while(sz[l]+1!=k) { if(sz[l]>=k) x=l; else k-=(sz[l]+1),x=r; l=ch[x][0],r=ch[x][1]; pushdown(l),pushdown(r); } return x; } //将链循环右移,使得x为链尾 void roll(int x) { splay(x); if(head[x]!=x) splay(head[x],x); if(!ch[x][0]) ch[x][0]=ch[x][1]; else { ch[head[x]][0]=ch[x][1]; if(ch[x][1]) { fa[ch[x][1]]=head[x]; pushup(head[x]); } } ch[x][1]=0; pushup(x); } //查x所在的链头 int findroot(int x) { while(fa[x]) x=fa[x]; return x; } //将x,y所在的链分裂,规则为分别截出(nxt[x])->y,(nxt[y])->x void split(int x,int y) { roll(x); splay(y,x); modify(mn[x],1); ch[x][0]=ch[y][1]; if(ch[y][1]) fa[ch[y][1]]=x,ch[y][1]=0; fa[y]=0; pushup(x),pushup(y); modify(mn[x],sz[x]); modify(mn[y],sz[y]); } //将x,y所在的链合并,规则为x->(nxt[y]) void merge(int x,int y) { roll(x),roll(y); modify(mn[x],1); modify(mn[y],1); ch[x][1]=y,fa[y]=x; pushup(x); modify(mn[x],sz[x]); } }spt; int n,q; int a[N]; char op[20]; int main() { int T; scanf("%d",&T); while(T--) { scanf("%d%d",&n,&q); t_sz=1; while(t_sz<n) t_sz<<=1; for(int i=1;i<(t_sz<<1);i++) t[i]=1; spt.init(); for(int i=1;i<=n;i++) a[i]=i,spt.sz[i]=1,spt.head[i]=spt.mn[i]=i; while(q--) { ll x,y; scanf("%s%lld%lld",op+1,&x,&y); if(op[1]=='s' && op[6]=='a') swap(a[x],a[y]); if(op[1]=='s' && op[6]=='p') { if(x==y) continue; if(spt.findroot(x)==spt.findroot(y)) spt.split(x,y); else spt.merge(x,y); } if(op[1]=='c') { int pos=1; ll diff=abs(x-y),qans=1; while(pos<t_sz) { if(merge(qans,t[pos<<1])==0 || diff%merge(qans,t[pos<<1])!=0) pos=pos<<1; else qans=merge(qans,t[pos<<1]),pos=pos<<1|1; } qans=merge(qans,t[pos]); pos=pos-t_sz+1+(qans==0 || diff%qans!=0?0:1); if(pos>n) printf("=\n"); else { spt.splay(pos); spt.roll(pos); int cyc=spt.sz[pos]; x=(x-2+2*cyc)%cyc+1; y=(y-2+2*cyc)%cyc+1; int px=spt.kth(pos,x); int py=spt.kth(pos,y); printf(a[px]<a[py]?"<\n":">\n"); } } } } return 0; }
CPC里面不怎么考Splay,可能是因为太裸了
继续看LCT去了
(完)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号