一些奇妙的线段树操作
学过数据结构和会做题完全是两个概念orz
各种各样的题目都应该见识一下
简单的目录:
最基本的应用是动态维护最大子段和
考虑对于一个$[L,R]$区间,被从正中分成两个子区间$[L,mid],[mid+1,R]$
那么$[L,R]$区间的最大子段区间只可能有三种来源:仅在$[L,mid]$中、仅在$[mid+1,R]$中、跨两个子区间
前两种来源很好处理,可以直接拿$[L,mid],[mid+1,R]$中的最大子段和来更新$[L,R]$中的
唯一比较麻烦的就是跨两个子区间的情况
此时,显然没有办法在只维护最大子段和的情况下解决这种情况,所以可以考虑多维护一些值
1. $l[k]$,表示$k$所对应的区间中,从最左端开始的最大区间和
2. $r[k]$,表示$k$所对应的区间中,从最右端开始的最大区间和
3. $sum[k]$,表示$k$所对应的区间 的区间和
这样一来,跨区间的情况就可以通过$max(0,r[k<<1])+max(0,l[k<<1\text{|} 1])$表示,即从$[L,mid]$的右端、$[mid+1,R]$的左端各取最大的一段,并拼起来
而$l$的维护不是很复杂,$l[k]=max(l[k<<1],sum[k<<1]+l[k<<1\text{|} 1])$,即要不取$[L,mid]$的左端,要不全取$[L,mid]$、同时拼上$[mid+1,R]$的左端
$r$同理,$sum$比较简单就不赘述了
一道例题:HDU 6638 ($Snowy\ Smile$,$2019\ Multi-University\ Training\ Contest\ 6$)
将坐标离散化后,考虑先确定矩形在$x$轴上的范围
可以对于一个上界$i$,依次枚举下界$j$,这样就能不重不漏地枚举出$\frac{n(n+1)}{2}$种矩形的上下界
可以将每一列的元素求和后看成一个数组,于是问题就转化为了动态维护区间最大子段和
由于一共只有$n$个箱子,每个箱子只会在每个上界$i$中被压入线段树一次,所以总复杂度是$O(n^2\cdot logn)$
注意应该在压完一整行后再更新答案,因为同一行的箱子是会互相影响的

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef pair<int,int> pii; typedef long long ll; const int N=2005; int n; int x[N],y[N],w[N]; void Change(int *a) { vector<int> vec; for(int i=1;i<=n;i++) vec.push_back(a[i]); sort(vec.begin(),vec.end()); vec.resize(unique(vec.begin(),vec.end())-vec.begin()); for(int i=1;i<=n;i++) a[i]=lower_bound(vec.begin(),vec.end(),a[i])-vec.begin()+1; } int sz; ll t[N<<2],l[N<<2],r[N<<2],sum[N<<2]; inline void Add(int k,int x) { k=k+sz-1; t[k]+=x; l[k]+=x; r[k]+=x; sum[k]+=x; k>>=1; while(k) { t[k]=max(t[k<<1],t[k<<1|1]); t[k]=max(t[k],max(r[k<<1],0LL)+max(l[k<<1|1],0LL)); l[k]=max(l[k<<1],sum[k<<1]+l[k<<1|1]); r[k]=max(r[k<<1|1],sum[k<<1|1]+r[k<<1]); sum[k]=sum[k<<1]+sum[k<<1|1]; k>>=1; } } vector<pii> v[N]; int main() { int T; scanf("%d",&T); while(T--) { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d%d%d",&x[i],&y[i],&w[i]); Change(x); Change(y); sz=1; while(sz<n) sz<<=1; for(int i=1;i<=n;i++) v[i].clear(); for(int i=1;i<=n;i++) v[x[i]].push_back(pii(y[i],w[i])); ll ans=0; for(int i=1;i<=n;i++) { memset(t,0,sizeof(t)); memset(l,0,sizeof(l)); memset(r,0,sizeof(r)); memset(sum,0,sizeof(sum)); for(int j=i;j<=n;j++) { for(int k=0;k<v[j].size();k++) Add(v[j][k].first,v[j][k].second); ans=max(ans,t[1]); } } printf("%lld\n",ans); } return 0; }
题目链接:HDU 3911 ($Black$ $And$ $White$)
题目大意:有一个长度为$n$($1\le n\le 10^5$)的$01$序列$a_i$,现在有$m$个操作:将区间$[l_i,r_i]$反转($01$互换),或询问区间$[l_i,r_i]$中$1$最多连续出现多少次
区间的反转很显然可以用懒标记解决,细节就不再赘述了
难办的是区间内的最大连续长度,原因在于,两段小区间如何合并成一个大区间并不容易想到
先考虑最大连续长度可能的来源
- 仅在左半区间
- 仅在右半区间
- 横跨两个小区间
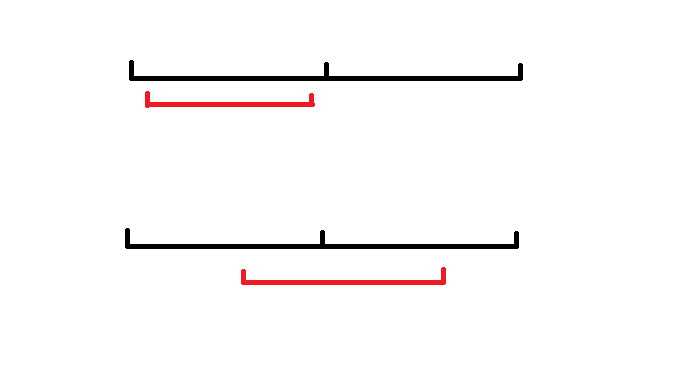
我们可以多记录一东西:除了当前区间内的最大连续长度,再记录当前区间内从最左端、最右端开始的最大连续长度
这样,如果我们想把两个小区间合并,得到的连续长度相当于是(左半区间从右端开始的最大长度+右半区间从左端开始的最大长度)
这两个新加的记录值也是容易合并的:求最左端开始的最大连续长度,如果左半区间全是相同数字,那么可以与右半区间的最左端合并,否则就是左半区间的最大连续长度;求最右端开始的亦是如此

#include <cstdio> #include <cmath> #include <cstring> #include <cstdlib> using namespace std; inline int max(int a,int b) { return (a>b?a:b); } inline int min(int a,int b) { return (a<b?a:b); } inline void swap(int &a,int &b) { int tmp=a; a=b,b=tmp; } const int MAX=100005; int n,m; int c[MAX<<1]; int sz; int left[MAX<<2][2],right[MAX<<2][2],mid[MAX<<2][2]; int tag[MAX<<2]; inline void Calc(int k,int a,int b) { int len=(b-a+1)>>1; for(int i=0;i<2;i++) { left[k][i]=left[k<<1][i]+(left[k<<1][i]==len?left[(k<<1)+1][i]:0); right[k][i]=right[(k<<1)+1][i]+(right[(k<<1)+1][i]==len?right[k<<1][i]:0); mid[k][i]=max(mid[k<<1][i],mid[(k<<1)+1][i]);//#1 mid[k][i]=max(mid[k][i],right[k<<1][i]+left[(k<<1)+1][i]); } } inline void Build(int k,int a,int b) { if(a==b) { left[k][c[a]]=right[k][c[a]]=mid[k][c[a]]=1; return; } Build(k<<1,a,(a+b)>>1); Build((k<<1)+1,((a+b)>>1)+1,b); Calc(k,a,b); } inline void Update(int k,int a,int b) { if(!tag[k]) return; swap(left[k][0],left[k][1]); swap(right[k][0],right[k][1]); swap(mid[k][0],mid[k][1]); tag[k]=0; if(a!=b) { tag[k<<1]^=1; tag[(k<<1)+1]^=1; } } inline void Modify(int k,int l,int r,int a,int b) { Update(k,a,b); if(a>r || b<l) return; if(a>=l && b<=r) { tag[k]^=1; Update(k,a,b); return; } Modify(k<<1,l,r,a,(a+b)>>1); Modify((k<<1)+1,l,r,((a+b)>>1)+1,b); Calc(k,a,b); } inline int Query(int k,int l,int r,int a,int b) { Update(k,a,b); if(a>r || b<l) return 0; if(a>=l && b<=r) return mid[k][1]; int half=(a+b)>>1; if(r<=half) return Query(k<<1,l,r,a,half); if(l>half) return Query((k<<1)+1,l,r,half+1,b); int midv=max(Query(k<<1,l,r,a,half),Query((k<<1)+1,l,r,half+1,b)); midv=max(midv,min(right[k<<1][1],half-l+1)+min(left[(k<<1)+1][1],r-half)); return midv; } int main() { // freopen("input.txt","r",stdin); while(~scanf("%d",&n)) { memset(left,0,sizeof(left)); memset(right,0,sizeof(right)); memset(mid,0,sizeof(mid)); memset(tag,0,sizeof(tag)); memset(c,0,sizeof(c)); for(int i=1;i<=n;i++) scanf("%d",&c[i]); sz=1; while(sz<n) sz<<=1; Build(1,1,sz); scanf("%d",&m); while(m--) { int op,x,y; scanf("%d%d%d",&op,&x,&y); if(op==1) Modify(1,x,y,1,sz); else printf("%d\n",Query(1,x,y,1,sz)); } } return 0; }
这种做法有一种明显的标志:有一种操作是用$min(a_i,w)$来取代$a_i$
经典模板题:HDU 5306($Gorgeous$ $Sequence$)
感谢这篇题解:https://www.cnblogs.com/shenben/p/6641984.html
做法的精髓是,不仅记录 当前节点表示的区间中 的最大值$x$和区间和$sum$(不然只是普通的线段树了),同时记录区间中最大值的出现次数$cnt$和严格次大值$y$
现在我们考虑如何处理题目中的$0$修改
首先通过递归,定位到某个严格包含在区间中的线段$t_k$,然后根据具体情况分为三种处理方式
- $t[k].x\le w$,即区间内的最大值也小于$w$,那么区间内的所有元素都不会改变,直接退出即可
- $t[k].y<w<t_k.x$,即区间内仅有最大值大于$w$,那么区间内的$t[k].cnt$个最大值都需要变成$w$,同时对$t[k].sum$做出更新($t[k].sum-=t[k].cnt\times (t[k].x-w)$,注意强制转换成long long)
- $t[k].y\le w$,即区间内有超过一种值大于等于$w$(如果$t[k].y==w$归于第2类,那么$t[k].cnt$不会更新),无法直接更新,需要向下继续递归结束后再重新计算来更新
同时我们发现,所有的更新仅限于第$2$类,其并没有进行到底,所以每个节点的$t[k].x$都有类似懒标记的作用,在修改与查询的过程中应当将这个懒标记向下更新
这个做法的复杂度没找到推导...虽然有人说$O(NlogN)$,但还是觉得$O(N(logN)^2)$更靠谱点

#include <cstdio> #include <cstring> #include <cmath> #include <algorithm> using namespace std; typedef long long ll; const int MAX=1000005; struct Node { int x,y,cnt; ll sum; Node(int a=0,int b=0,int c=-1,ll d=0LL) { x=a,y=b,cnt=c,sum=d; } }; int n,m; int val[MAX<<1]; Node t[MAX<<2]; inline void Update(int k) { int left=k<<1,right=left+1; t[k].sum=t[left].sum+t[right].sum; if(t[left].x==t[right].x) { t[k].x=t[left].x; t[k].y=max(t[left].y,t[right].y); t[k].cnt=t[left].cnt+t[right].cnt; } else { if(t[left].x<t[right].x) swap(left,right); t[k].x=t[left].x; t[k].y=max(t[left].y,t[right].x); t[k].cnt=t[left].cnt; } } inline void Build(int k,int a,int b) { if(a==b) { t[k]=Node(val[a],-1,1,val[a]); return; } Build(k<<1,a,(a+b)>>1); Build((k<<1)+1,((a+b)>>1)+1,b); Update(k); } inline void Dec(int k,int x) { if(t[k].x<=x) return; t[k].sum-=(ll)t[k].cnt*(t[k].x-x); t[k].x=x; } inline void Pushdown(int k) { Dec(k<<1,t[k].x); Dec(k<<1|1,t[k].x); } inline void Modify(int k,int l,int r,int a,int b,int w) { if(a>r || b<l) return; if(a>=l && b<=r)//*** { if(t[k].x<=w) return; if(t[k].y<w)//*** { Dec(k,w); return; } } Pushdown(k); Modify(k<<1,l,r,a,(a+b)>>1,w); Modify(k<<1|1,l,r,((a+b)>>1)+1,b,w); Update(k); } inline int Max(int k,int l,int r,int a,int b) { if(a>r || b<l) return 0; if(a>=l && b<=r) return t[k].x; Pushdown(k); return max(Max(k<<1,l,r,a,(a+b)>>1),Max(k<<1|1,l,r,((a+b)>>1)+1,b)); } inline ll Sum(int k,int l,int r,int a,int b) { if(a>r || b<l) return 0; if(a>=l && b<=r) return t[k].sum; Pushdown(k); return Sum(k<<1,l,r,a,(a+b)>>1)+Sum(k<<1|1,l,r,((a+b)>>1)+1,b); } int main() { // freopen("input.txt","r",stdin); int T; scanf("%d",&T); while(T--) { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&val[i]); int sz=1; while(sz<n) sz<<=1; Build(1,1,sz); while(m--) { int op,x,y,w; scanf("%d%d%d",&op,&x,&y); if(op==0) { scanf("%d",&w); Modify(1,x,y,1,sz,w); } if(op==1) printf("%d\n",Max(1,x,y,1,sz)); if(op==2) printf("%lld\n",Sum(1,x,y,1,sz)); } for(int i=1;i<=n;i++) val[i]=0; for(int i=1;i<sz+n;i++) t[i]=Node(); } return 0; }
一道更加综合的题:BZOJ 4695 (最假女选手)
这道题目就是上一题的加强版了,不仅有区间取$min$,还有区间加,区间取$max$
所以我们不仅要保存区间和、最大值、次大值、最大值出现次数,还要保存最小值、次小值、最小值出现次数、区间加的懒标记(貌似最后一个可以不用?有时间研究一下...)
虽然大家保存的节点结构都差不多,但后面的标记传递还是有点差距的(我的写法虽然常数巨大,但是竟然能省略很多细节)
首先考虑区间加(操作$1$)
跟普通的线段树区间加是一样的操作:先定位,然后给$tag$加上这个数,并改变$sum$;每次将要访问下层节点的时候,将$tag$向下传递
但是这道题中tag的存在感比普通的区间加中的要强很多,因为对于每个线段树节点,最值、次最值都是相对值,真实的值需要加上这个节点的$tag$(这个在操作$2$、$3$出现)
然后是区间取$min$(操作$3$) <-跟上一题一样,讲起来方便
先递归到严格区间内,然后分三步操作(比较的时候记得加上$tag$)
但是这里存在比上一题麻烦的地方:修改区间最大、次大值的同时,我们还有可能改变区间的最小、次小值
别的大佬们在这里就直接讨论了,但我写的时候没有想那么多(怀疑常数出现在这里)
我们先考虑一下,在什么时候才会从操作$3$的递归进入对单点的修改?
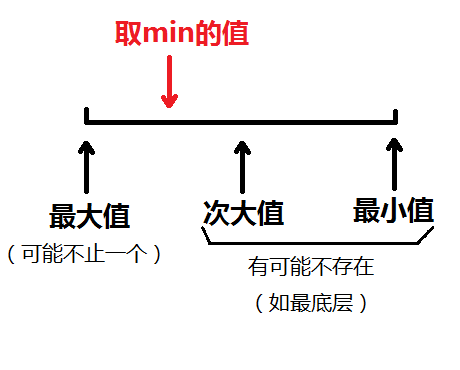
这下,最小、次小值改变的条件就清晰一些了
- 如果存在次小值,且最大值等于次小值,次小值改变,最小值不变
- 如果不存在次小值(即区间内全是最大值,此时最小值也是最大值),那么最小值改变,次小值仍不存在
- 否则(即次小值存在且小于最大值),最小值、次小值都不改变
区间取$max$(操作$2$)是这个的镜像操作,别写岔就行了
要记得将$tag$、小值、大值向下传递(与前一题差不多),并在递归后更新节点(我写的巨丑,也是大常数的来源...有必要再学习一下别人的代码)
这题跑了$46000+MS$,快反向登顶了,哎...

#include <cstdio> #include <cstring> #include <cmath> #include <ctime> #include <algorithm> using namespace std; typedef long long ll; const int MAX=500005; const int INF=1<<30; struct Node { ll sum; int tag,len; int fst[2],sec[2],cnt[2]; Node() { fst[0]=sec[0]=-INF; fst[1]=sec[1]=INF; cnt[0]=cnt[1]=sum=tag=len=0; } Node(int x) { fst[0]=fst[1]=x; sec[0]=-INF,sec[1]=INF; cnt[0]=cnt[1]=len=1; sum=x,tag=0; } }; int n,m,sz=1; int val[MAX<<1]; Node t[MAX<<2]; inline void Update(int k) { Node l=t[k<<1],r=t[k<<1|1]; t[k].sum=l.sum+r.sum; for(int i=0;i<2;i++) { l.fst[i]=l.fst[i]+l.tag-t[k].tag; l.sec[i]=l.sec[i]+l.tag-t[k].tag; r.fst[i]=r.fst[i]+r.tag-t[k].tag; r.sec[i]=r.sec[i]+r.tag-t[k].tag; if(l.fst[i]==r.fst[i]) { t[k].fst[i]=l.fst[i]; if(i==0) t[k].sec[i]=max(l.sec[i],r.sec[i]); else t[k].sec[i]=min(l.sec[i],r.sec[i]); t[k].cnt[i]=l.cnt[i]+r.cnt[i]; } else { if(i==0 && l.fst[i]<r.fst[i]) swap(l,r); if(i==1 && l.fst[i]>r.fst[i]) swap(l,r); t[k].fst[i]=l.fst[i]; if(i==0) t[k].sec[i]=max(l.sec[i],r.fst[i]); else t[k].sec[i]=min(l.sec[i],r.fst[i]); t[k].cnt[i]=l.cnt[i]; } } } inline void Build(int k,int r,int a,int b) { if(a>r) return; if(a==b) { t[k]=Node(val[a]); return; } Build(k<<1,r,a,(a+b)>>1); Build(k<<1|1,r,((a+b)>>1)+1,b); Update(k); t[k].len=t[k<<1].len+t[k<<1|1].len; } inline void DecMax(int k,ll w) { w-=t[k].tag; if(t[k].fst[0]<=w) return; t[k].sum-=(ll)t[k].cnt[0]*(t[k].fst[0]-w); if(t[k].fst[0]==t[k].sec[1]) t[k].sec[1]=w; if(t[k].fst[0]==t[k].fst[1]) t[k].fst[1]=w; t[k].fst[0]=w; } inline void DecMin(int k,ll w) { w-=t[k].tag; if(t[k].fst[1]>=w) return; t[k].sum-=(ll)t[k].cnt[1]*(t[k].fst[1]-w); if(t[k].fst[1]==t[k].sec[0]) t[k].sec[0]=w; if(t[k].fst[1]==t[k].fst[0]) t[k].fst[0]=w; t[k].fst[1]=w; } inline void DecTag(int k) { if(t[k].tag==0) return; for(int i=0;i<2;i++) { t[k].fst[i]+=t[k].tag; t[k].sec[i]+=t[k].tag; } if(k<sz) { t[k<<1].tag+=t[k].tag; t[k<<1].sum+=(ll)t[k].tag*t[k<<1].len; t[k<<1|1].tag+=t[k].tag; t[k<<1|1].sum+=(ll)t[k].tag*t[k<<1|1].len; } t[k].tag=0; } inline void Down(int k) { DecTag(k); DecMax(k<<1,t[k].fst[0]); DecMin(k<<1,t[k].fst[1]); DecMax(k<<1|1,t[k].fst[0]); DecMin(k<<1|1,t[k].fst[1]); } inline void Add(int k,int l,int r,int a,int b,int w) { if(a>r || b<l) return; if(a>=l && b<=r) { t[k].tag+=w; t[k].sum+=(ll)t[k].len*w; return; } Down(k); Add(k<<1,l,r,a,(a+b)>>1,w); Add(k<<1|1,l,r,((a+b)>>1)+1,b,w); Update(k); } inline void ModifyMax(int k,int l,int r,int a,int b,int w) { if(a>r || b<l) return; if(a>=l && b<=r) { if(t[k].fst[1]+t[k].tag>=w) return; if(t[k].sec[1]+t[k].tag>w) { DecMin(k,w); return; } } Down(k); ModifyMax(k<<1,l,r,a,(a+b)>>1,w); ModifyMax(k<<1|1,l,r,((a+b)>>1)+1,b,w); Update(k); } inline void ModifyMin(int k,int l,int r,int a,int b,int w) { if(a>r || b<l) return; if(a>=l && b<=r) { if(t[k].fst[0]+t[k].tag<=w) return; if(t[k].sec[0]+t[k].tag<w) { DecMax(k,w); return; } } Down(k); ModifyMin(k<<1,l,r,a,(a+b)>>1,w); ModifyMin(k<<1|1,l,r,((a+b)>>1)+1,b,w); Update(k); } inline ll QuerySum(int k,int l,int r,int a,int b) { if(a>r || b<l) return 0LL; if(a>=l && b<=r) return t[k].sum; Down(k); return QuerySum(k<<1,l,r,a,(a+b)>>1)+QuerySum(k<<1|1,l,r,((a+b)>>1)+1,b); } inline int QueryMax(int k,int l,int r,int a,int b) { if(a>r || b<l) return -INF; if(a>=l && b<=r) return t[k].fst[0]+t[k].tag; Down(k); return max(QueryMax(k<<1,l,r,a,(a+b)>>1),QueryMax(k<<1|1,l,r,((a+b)>>1)+1,b)); } inline int QueryMin(int k,int l,int r,int a,int b) { if(a>r || b<l) return INF; if(a>=l && b<=r) return t[k].fst[1]+t[k].tag; Down(k); return min(QueryMin(k<<1,l,r,a,(a+b)>>1),QueryMin(k<<1|1,l,r,((a+b)>>1)+1,b)); } int main() { // freopen("input.txt","r",stdin); // freopen("my.txt","w",stdout); scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&val[i]); while(sz<n) sz<<=1; Build(1,n,1,sz); scanf("%d",&m); while(m--) { int op,x,y,w; scanf("%d%d%d",&op,&x,&y); if(op<4) scanf("%d",&w); if(op==1) Add(1,x,y,1,sz,w); if(op==2) ModifyMax(1,x,y,1,sz,w); if(op==3) ModifyMin(1,x,y,1,sz,w); if(op==4) printf("%lld\n",QuerySum(1,x,y,1,sz)); if(op==5) printf("%d\n",QueryMax(1,x,y,1,sz)); if(op==6) printf("%d\n",QueryMin(1,x,y,1,sz)); } return 0; }
这个一开始学起来真的有点困难...稍微有点抽象
在我的感觉中,是处理有关元素的有序性的问题的
例如将两个区间$[1,8]$的统计元素出现次数的线段树合并
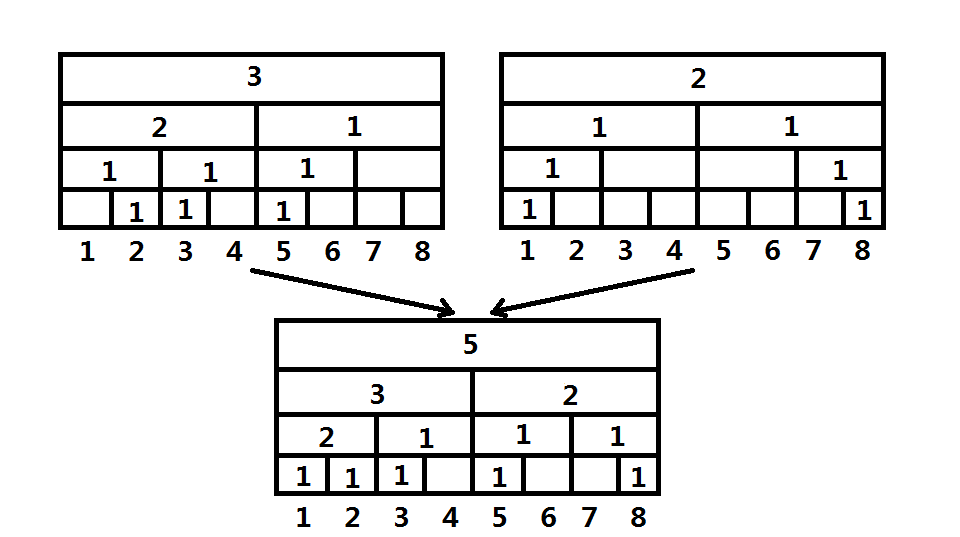
我们先想想如何实现
为了防止空间爆炸,我们写的线段树必然是动态开点的,那么便有一大优势:可以类似可持久化线段树一样,通过将新节点的儿子指向已经存在的某节点来重复利用
在这个基础上考虑将两棵线段树对于一个区间的两个节点$x$、$y$合并成一个新节点
- 若$x$、$y$都为空,则合并后也为空
- 若$x$、$y$其中一个为空,那么可以直接指向不为空的节点(因为与空树合并,原本的结构不变)
- 若$x$、$y$都不为空,那么分为左、右儿子继续向下递归,最后在将左右的统计值相加
(其实还是有很多细节的,最好学习写法比较好的代码,比如后面引用到的)
这样下来,复杂度是怎么样的呢?
首先一般情况,如果一颗数值区间为$[1,n]$的线段树是由$n$条链依次合并成的,那么就跟可持久化线段树一样,是$O(NlogN)$的时间复杂度
但是总有特例吧,比如下图,两棵线段树在叶节点互补(意会一下)
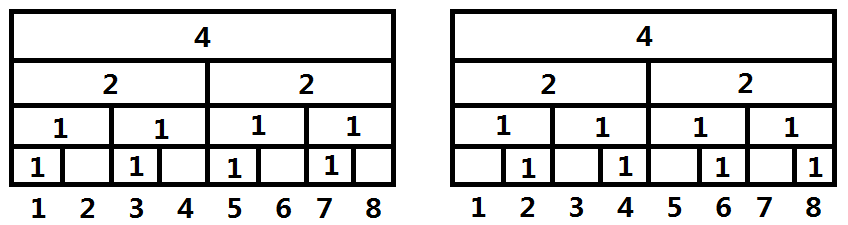
这样的一次合并是$O(N)$的
但是不要着急,如果想构成这样的情形,首先这两个树应当分别构造,且如果想让单次合并的消耗尽量大,在叶节点处应当同样互补
这样总的算下来,时间复杂度是$O(N+2\times \frac{N}{2}+4\times \frac{N}{4}+...)=O(NlogN)$,可以放心食用
由于合并大多伴随着开点,所以空间复杂度也是$O(NlogN)$,应当注意不要MLE
说了这么多,具体代码怎么实现比较好,又有什么用呢?
且看这道题目:BZOJ 2212 ($POI2011$,$Tree Rotations$)
我完全看的是这篇题解:胡小兔:神奇的操作——线段树合并(例题: BZOJ2212)
具体题目分析和代码实现都无可挑剔,我就不做无用功了
但是仅仅做出这一道题离熟练掌握还差距很大
再来一道题目:BZOJ 4552 ($TJoi2016$ & $HEoi2016$,排序)
准备学习一下这份代码:fjzzq2002:线段树合并与分裂
这道题目更加综合一些,不仅要求线段树的合并,还有分裂
其实在掌握合并的基础上,分裂也是容易处理的
加入我们想在以$root$为根的线段树上将第$p$个元素(包含第$p$个)分裂成一颗新树,就可以类似主席树上找第$k$大的递归处理
对于当前节点$x$($t_x$表示,节点$x$覆盖的区间共有多少元素)
- 若$t_{l_i}\le p$,那么第$p$个元素一定在$x$的左儿子中,将$r_x$直接割给新树
- 若$t_{l_i}>p$,那么第$p$个元素一定在$x$的右儿子中
- 若已经到达底端,则此时$x$就是以$root$为根的线段树中第$p$个元素,将$x$割给新树(在这里,我的实现是将$t_x$清零,将新树中对于节点$t_{cur}$赋成$1$)
然后可以删去一些分裂中被割走的节点:如果对于当前节点$x$,$t_{l_x}==0$,即左子树为空,那么令$l_x=0$以免之后的合并访问到这个没必要经过的节点;对于$r_x$同理
在这题中,除去了线段树的合并与分裂(总体应该是$O(NlogN)$,但是具体不会证),我们还需要一种数据结构告诉我们应该合并哪些线段树
一开始的想法是用一颗区间赋值线段树给合并后的每一段打上懒标记,但是如果想要从一段合并区间到另一段,感觉上需要在树上累加,应该是$O(logN)$的跳转,细节还很多
zzq给出的思路是用set,排序的依据是区间的左端点
这样一来,我们对每次排序的$[op,x,y]$操作,能够直接二分$O(logN)$的找出左右端点所在的合并区间,然后再通过$iterator$遍历将线段树合并
(不过我对set十分陌生,一开始将s.lower_bound(x)写成lower_bound(s.begin(),s.end(),x),应该是不能这样用的)
他是set<int>,我写的是set<pair<int,int> >,细节还非常的繁琐...应当学习一下他的处理方法
除去set的部分,我的代码还是能看的

#include <cstdio> #include <cstring> #include <cmath> #include <cstdlib> #include <algorithm> #include <set> using namespace std; typedef pair<int,int> pii; const int MAX=100005; const int LOG=100; int tot; int l[MAX*LOG],r[MAX*LOG],t[MAX*LOG],rev[MAX*LOG]; inline int Build(int x,int a,int b) { int cur=++tot; t[cur]=1; if(a==b) return cur; int mid=(a+b)>>1; if(x<=mid) l[cur]=Build(x,a,mid); else r[cur]=Build(x,mid+1,b); return cur; } inline int Merge(int x,int y,int a,int b) { if(!x || !y) return x+y; int cur=++tot,mid=(a+b)>>1; l[cur]=Merge(l[x],l[y],a,mid); r[cur]=Merge(r[x],r[y],mid+1,b); t[cur]=t[l[cur]]+t[r[cur]]; return cur; } inline void Update(int x) { if(!t[l[x]]) l[x]=0; if(!t[r[x]]) r[x]=0; } inline int Split(int x,int a,int b,int p) { int cur=++tot,mid=(a+b)>>1; if(a==b) { t[cur]=t[x]; t[x]=0; return cur; } if(t[l[x]]>=p) { l[cur]=Split(l[x],a,mid,p); r[cur]=r[x]; r[x]=0; } else r[cur]=Split(r[x],mid+1,b,p-t[l[x]]); Update(x); Update(cur); t[x]=t[l[x]]+t[r[x]]; t[cur]=t[l[cur]]+t[r[cur]]; return cur; } inline int Locate(int x,int a,int b,int p) { if(a==b) return a; int mid=(a+b)>>1; if(t[l[x]]>=p) return Locate(l[x],a,mid,p); else return Locate(r[x],mid+1,b,p-t[l[x]]); } int n,m,sz=1; int val[MAX]; set<pii> s; int main() { // freopen("input.txt","r",stdin); // freopen("output.txt","w",stdout); scanf("%d%d",&n,&m); while(sz<n) sz<<=1; for(int i=1;i<=n;i++) { scanf("%d",&val[i]); s.insert(pii(i,Build(val[i],1,sz))); } for(int i=1;i<=m;i++) { int op,x,y; scanf("%d%d%d",&op,&x,&y); set<pii>::iterator beg=s.lower_bound(pii(x,0)); if((*beg).first>x || beg==s.end()) beg--; set<pii>::iterator end=s.lower_bound(pii(y,0)); if((*end).first>y || end==s.end()) end--; int idx1=(*beg).second,left1=(*beg).first,idx2=(*end).second,left2=(*end).first; if(idx1==idx2) { s.erase(beg); int p1=x-left1+1,p2=y-left1+2; int rp1=t[idx1]-(x-left1)+1,rp2=t[idx1]-(y-left1); int left,right,mid; if(!rev[idx1]) { left=idx1,mid=Split(idx1,1,sz,p1),right=Split(mid,1,sz,p2-p1+1); if(t[left]) s.insert(pii(left1,left)); if(t[right]) s.insert(pii(y+1,right)); s.insert(pii(x,mid)); } else { left=idx1,mid=Split(idx1,1,sz,rp2),right=Split(mid,1,sz,rp1-rp2+1); if(t[left]) s.insert(pii(y+1,left)); if(t[right]) s.insert(pii(left1,right)); rev[left]=rev[right]=1; s.insert(pii(x,mid)); } rev[mid]=op; continue; } int num1=left1+t[idx1]-x,num2=y-left2+1; int p1=t[idx1]-num1+1,p2=num2+1; int rp1=num1+1,rp2=t[idx2]-num2+1; int begn,endn,rem1,rem2,newn; if(!rev[idx1]) begn=Split(idx1,1,sz,p1),rem1=idx1; else begn=idx1,rem1=Split(idx1,1,sz,rp1),rev[rem1]=1;// if(!rev[idx2]) endn=idx2,rem2=Split(idx2,1,sz,p2); else endn=Split(idx2,1,sz,rp2),rem2=idx2,rev[rem2]=1;// newn=Merge(begn,endn,1,sz); set<pii>::iterator it=beg; it++; while(it!=end) newn=Merge(newn,(*it).second,1,sz),it++; s.erase(beg,end); s.erase(end); if(t[rem1]) s.insert(pii(left1,rem1)); if(t[rem2]) s.insert(pii(y+1,rem2)); s.insert(pii(x,newn)); rev[newn]=op; } int q; scanf("%d",&q); set<pii>::iterator it=s.lower_bound(pii(q,0)); if((*it).first>q || it==s.end())// it--; int x=(*it).second,left=(*it).first; int p=(rev[x]?t[x]-(q-left):q-left+1); printf("%d\n",Locate(x,1,sz,p)); return 0; }
这题还有一种玩法是$O(N(logN)^2)$的二分+线段树区间修改,网上大部分都是这样的题解,也是一种有趣的思路吧

#include <cstdio> #include <cstring> #include <cmath> using namespace std; const int MAX=100005; int n,m,q; int val[MAX],op[MAX],ql[MAX],qr[MAX]; int c[MAX]; int sz=1; int t[MAX<<2],len[MAX<<2],tag[MAX<<2]; inline void Build(int k,int l,int r) { if(l==r) { if(l<=n) { t[k]=c[l]; len[k]=1; } return; } int mid=(l+r)>>1; Build(k<<1,l,mid); Build(k<<1|1,mid+1,r); t[k]=t[k<<1]+t[k<<1|1]; len[k]=len[k<<1]+len[k<<1|1]; } inline void Update(int x) { if(!tag[x]) return; t[x<<1]=(tag[x]>0?len[x<<1]:0); tag[x<<1]=tag[x]; t[x<<1|1]=(tag[x]>0?len[x<<1|1]:0); tag[x<<1|1]=tag[x]; tag[x]=0; } inline int Query(int k,int l,int r,int a,int b) { if(a>r || b<l) return 0; if(a>=l && b<=r) return t[k]; Update(k); int mid=(a+b)>>1; return Query(k<<1,l,r,a,mid)+Query(k<<1|1,l,r,mid+1,b); } inline void Add(int k,int l,int r,int a,int b,int w) { if(a>r || b<l) return; if(a>=l && b<=r) { tag[k]=w; t[k]=(w>0?len[k]:0); return; } Update(k); int mid=(a+b)>>1; Add(k<<1,l,r,a,mid,w); Add(k<<1|1,l,r,mid+1,b,w); t[k]=t[k<<1]+t[k<<1|1];// } int Check(int x) { memset(tag,0,sizeof(tag)); for(int i=1;i<=n;i++) c[i]=(val[i]<=x); Build(1,1,sz); for(int i=1;i<=m;i++) { int x=ql[i],y=qr[i],num=Query(1,x,y,1,sz); if(op[i]==0) { Add(1,x,x+num-1,1,sz,1); Add(1,x+num,y,1,sz,-1); } else { Add(1,x,y-num,1,sz,-1); Add(1,y-num+1,y,1,sz,1); } } return Query(1,q,q,1,sz); } int main() { // freopen("input.txt","r",stdin); // freopen("output.txt","w",stdout); scanf("%d%d",&n,&m); while(sz<n) sz<<=1; for(int i=1;i<=n;i++) scanf("%d",&val[i]); for(int i=1;i<=m;i++) scanf("%d%d%d",&op[i],&ql[i],&qr[i]); scanf("%d",&q); int l=1,r=n,mid; while(l<r) { mid=(l+r)>>1; if(Check(mid)) r=mid; else l=mid+1; } if(!Check(l)) l++; printf("%d\n",l); return 0; }
(完)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号