Prufer序列
参考了:Matrix67 - 经典证明:Prüfer编码与Cayley公式
是一种挺有意思的转化
在无向图中构造无根树时,如果限制条件比较简单,Prufer序列是可以完全替代矩阵树定理的
~ Prufer编码 ~
Prufer编码,是一种对于带标号无根树的编码,使得一个Prufer序列$p$能够唯一对应一棵带标号无根树,且不重不漏
编码方式是这样的:
对于一棵$n$个节点的带标号无根树($n\geq 2$),我们每次找到标号最小的叶节点,将其所连接的非叶节点的标号添加进序列,然后删去这个叶节点;不断这样循环,直到剩余节点数为$2$
由于这个做法将$n$个节点的树删成$2$个节点,所以得到的Prufer序列的长度为$n-2$
引用Matrix67的例子:对于以下带标号无根树求Prufer序列

1. 先把所有叶节点全部拎出来,发现为$\{4,7,8,9\}$,其中节点$4$最小,于是将节点$4$所连接的非叶节点$3$加入序列、并删去节点$4$;序列$p$暂时为$\{3\}$
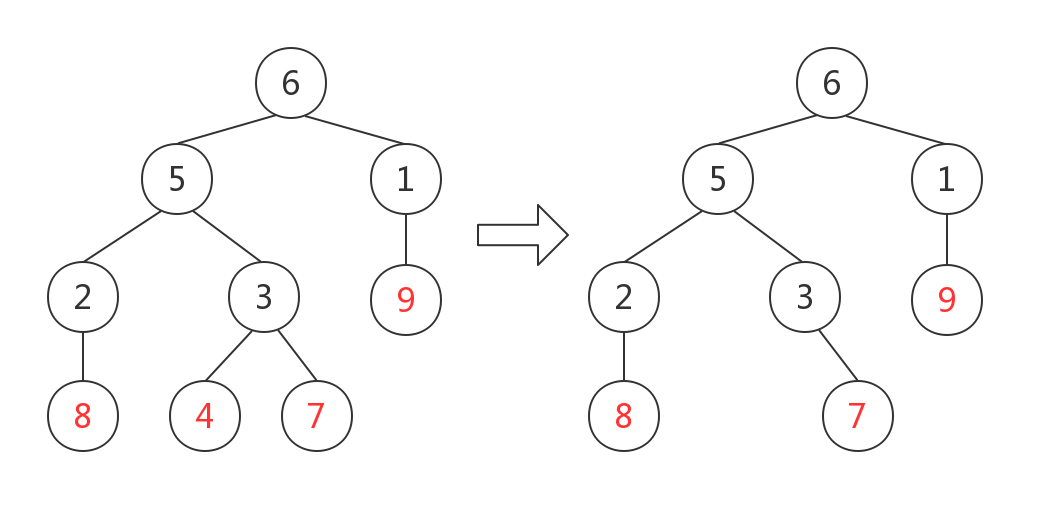
2. 此时的叶节点有$\{7,8,9\}$,将$7$所连接的非叶节点$3$加入序列、并删去节点$7$;序列$p$暂时为$\{3,3\}$

3. 此时的叶节点有$\{3,8,9\}$,将节点$3$所连接的非叶节点$5$加入序列、并删去节点$3$;序列$p$暂时为$\{3,3,5\}$

4. 之后不断重复这个过程,最终得到Prufer序列$p=\{3,3,5,2,5,6,1\}$

上面我们提到了 一个Prufer序列唯一对应一棵有标号的无根树
那么给定一个Prufer序列时,如何构造对应的树呢?其实和上面的做法是十分类似的
首先我们有一个性质:在Prufer序列$p$中的节点为无根树中的非叶节点,不在$p$中的节点为叶节点
这是显然的,因为叶节点只会被删去,而每次加入序列的点都是叶节点所连接的非叶节点
然后可以将这个性质稍加推广:在子序列$p[i...n-2]$中的节点为操作过$i-1$次的无根树中的非叶节点,不在$p[i...n-2]$中、且未被前$i-1$次操作删去的节点为叶节点
这又可以推出另一个性质:Prufer序列所确定的无根树,节点$i$的度数等于$i$在Prufer序列中出现次数+1
那么我们可以维护当前无根树的叶节点集合,而集合中的最小元素就是将被删去的叶节点
multiset<int> nleaf,leaf; for(int i=1;i<=n-2;i++) nleaf.insert(p[i]); for(int i=1;i<=n;i++) if(nleaf.find(i)==nleaf.end()) leaf.insert(i); for(int i=1;i<=n-2;i++) { printf("%d %d\n",*leaf.begin(),p[i]); leaf.erase(leaf.begin()); nleaf.erase(nleaf.find(p[i])); if(nleaf.find(p[i])==nleaf.end()) leaf.insert(p[i]); } printf("%d %d\n",*leaf.begin(),*(++leaf.begin()));
利用Prufer序列,我们尝试证明Cayley公式
Cayley公式指的是,$n$阶完全图$K_n$有$n^{n-2}$棵生成树;或者说$n$个节点的带标号无根树有$n^{n-2}$棵
这里的幂次$n-2$让我们很眼熟,因为这恰是Prufer序列的长度;那么$n^{n-2}$就代表着,$n-2$个位置任意填$[1,n]$中的数,都可以构成Prufer序列
事实上也确实是这样的,因为我们总能保证叶节点集合的大小至少为$2$——在$p[i...n-2]$中出现的非叶节点数加上已删去的$i-1$个叶节点最多只有$n-2$个,剩余的至少$2$个节点均为当前无根树的叶节点;所以这$n^{n-2}$个序列均为合法的Prufer序列
而一个Prufer序列唯一对应一个带标号无根树,那么Cayley公式得证
还有一个奇妙的结论是,一个度数序列为$\{d_1,d_2,...,d_n\}$的带标号无根树共有$\frac{(n-2)!}{\prod_{i=1}^{n} (d_i-1)!}$棵
证明比较容易:
一个度数序列为$d_i$的节点必会在Prufer序列中出现$d_i-1$次,那么不妨从$i=1$开始计算;要满足$1$号节点的度数为$d_1$,就需要在Prufer序列的$n-2$个位置中选$d_1-1$个填$1$,则有$\begin{pmatrix} n-2\\d_1-1\end{pmatrix}$中选法;而$i=2$时需要从剩余的$(n-2)-(d_1-1)$个位置中选$d_2-1$个,有$\begin{pmatrix} (n-2)-(d_1-1)\\d_2-1\end{pmatrix}$……将组合数用阶乘展开,就是$\frac{(n-2)!}{(d_1-1)![(n-2)-(d_1-1)]!}\cdot \frac{[(n-2)-(d_1-1)]!}{(d_2-1)![(n-2)-(d_1-1)-(d_2-1)]!}\cdot ...$,即为上面的结论
~ 一些题目 ~
BZOJ 1005 (明明的烦恼,$HNOI2008$)
先把$d_i\neq -1$的情况按照上面的方法用阶乘展开,那么$n-2-\sum_{d_i\neq -1} (d_i-1)$个未被选的位置就可以任意填$d_i=-1$的$i$
这题本来需要高精度乘除,但是由于$n$很小,所以可以在阶乘展开式中统计每个数被乘了几次,然后质因数分解,这样就只需要处理高精乘了

#include <cstdio> #include <vector> #include <algorithm> using namespace std; const int N=1005; int n,cnt,sum; int d[N]; vector<int> fac[N]; int val[N]; int len,bignum[3*N]; int main() { for(int i=2;i<N;i++) { int x=i; for(int j=2;j*j<=x;j++) while(x%j==0) { fac[i].push_back(j); x/=j; } if(x>1) fac[i].push_back(x); } scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&d[i]); if(d[i]>0) cnt++,sum+=d[i]; if(d[i]>=n || d[i]==0) { printf("0\n"); return 0; } } if(sum+n-cnt>2*n-2 || (cnt==n && sum!=2*n-2)) printf("0\n"); else { int rem=n-2; for(int i=1;i<=n;i++) { if(d[i]<0) continue; for(int j=1;j<=rem;j++) val[j]++; for(int j=1;j<=d[i]-1;j++) val[j]--; for(int j=1;j<=rem-(d[i]-1);j++) val[j]--; rem-=(d[i]-1); } val[n-cnt]+=rem; for(int i=1;i<=n;i++) if(fac[i].size()>1) { for(int j=0;j<fac[i].size();j++) val[fac[i][j]]+=val[i]; val[i]=0; } len=1,bignum[1]=1; for(int i=2;i<=n;i++) for(int j=1;j<=val[i];j++) { int carry=0; for(int k=1;k<=len;k++) { int tmp=bignum[k]*i+carry; bignum[k]=tmp%10; carry=tmp/10; if(carry) len=max(len,k+1); } } for(int i=len;i>=1;i--) printf("%d",bignum[i]); } return 0; }
HDU 5629 ($Clarke\ and\ tree$)
看到这种计算方案数的题目,就能想到是DP
首先很明显需要两维$i,k$分别表示选择到了节点$i$、Prufer序列中已填过了$k$个位置(这里的Prufer序列没有固定的长度,而是仅仅是一个可以插入数值的序列);但是仅仅两维不足以表示状态,因为我们无法知道当前一共选中了多少个节点(度数为$1$的点不会对$k$产生影响),所以需要再加一维$j$表示一共选中了$j$个节点
那么$dp[i][j][k]$有两种转移方式,分别是选中/不选中节点$i$
若不选中节点$i$,那么有$dp[i+1][j][k]+=dp[i][j][k]$
若选中节点$i$,那么可以对$dp[i+1][j+1][l]$产生贡献(向$l$转移时需要考虑$a[i]$的限制);那么就相当于向之前长度为$k$的Prufer序列中插入$l-k$个$i$,这可以看成有$l$个位置,先选择$l-k$个填$i$,剩下$k$个依次填之前的Prufer序列,于是贡献为$\begin{pmatrix}l\\l-k\end{pmatrix}$
于是转移方程为$dp[i+1][j+1][l]+=dp[i][j][k]\cdot \begin{pmatrix}l\\l-k\end{pmatrix}$
那么最终选择$i(i\geq 2)$个节点的答案为$dp[n+1][i][i-2]$;当$i=1$时答案为$n$

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=55; const int MOD=1000000007; ll C[N][N]; int n; int a[N]; ll dp[N][N][N]; int main() { for(int i=0;i<N;i++) C[i][0]=C[i][i]=1; for(int i=1;i<N;i++) for(int j=1;j<i;j++) C[i][j]=(C[i-1][j]+C[i-1][j-1])%MOD; int T; scanf("%d",&T); while(T--) { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); memset(dp,0,sizeof(dp)); dp[1][0][0]=1; for(int i=1;i<=n;i++) for(int j=0;j<i;j++) for(int k=0;k<=n-2;k++) { if(!dp[i][j][k]) continue; dp[i+1][j][k]=(dp[i+1][j][k]+dp[i][j][k])%MOD; for(int l=k;l<=n-2 && l-k<a[i];l++) dp[i+1][j+1][l]=(dp[i+1][j+1][l]+dp[i][j][k]*C[l][l-k])%MOD; } printf("%d ",n); for(int i=2;i<=n;i++) printf("%d",dp[n+1][i][i-2]),putchar(i==n?'\n':' '); } return 0; }
CF 156D ($Clues$)
在通过Prufer序列恢复带标号无根树的过程中,我们是将节点相连构成一棵树
而在这题中,我们有许多连通块;如果我们将每一个连通块缩成一个点,那么就相当于将缩点相连构成一棵树
那么我们就可以将Prufer序列进行推广
假设有$m$个连通块,其中每个连通块的大小为$s[i]$($1\leq i\leq m$),那么推广的Prufer序列长度为$m-2$
在每一个位置,我们可以任意填$x\in [1,n]$,表示有一个缩点与$x$所在的缩点相连
这样填完以后,我们就得到了缩点之间的相连关系(其中非叶缩点的连接处确定),但是我们并不知道叶缩点的连接处是什么
事实上,叶缩点的连接处可以是这个连通块的任意节点,即有连通块大小种连接方式;那么长度为$m-2$的序列就能确定$m-2$个叶缩点的连接方式
现在唯一没有确定的就是最后剩下来的$2$个缩点了;不过他们之间也可以随意连,所以连接方式为两连通块大小之积
于是答案为$n^{m-2}\cdot \prod_{i=1}^{m} s[i]$,十分奥妙

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=100005; int n,m,k; vector<int> v[N]; bool vis[N]; void dfs(int x,int &sz) { sz++; vis[x]=true; for(int i=0;i<v[x].size();i++) { int y=v[x][i]; if(!vis[y]) dfs(y,sz); } } int main() { scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=m;i++) { int x,y; scanf("%d%d",&x,&y); v[x].push_back(y); v[y].push_back(x); } ll ans=1; int cnt=0,sz; for(int i=1;i<=n;i++) if(!vis[i]) { cnt++,sz=0; dfs(i,sz); ans=ans*sz%k; } for(int i=1;i<=cnt-2;i++) ans=ans*n%k; printf("%lld\n",cnt==1?1LL%k:ans); return 0; }
ZOJ 4069 ($Sub-cycle\ Graph$,$2018ICPC$青岛)
Prufer序列+生成函数
CF 917D ($Stranger\ Tree$)
首先先做了一个转化,本来要求的$ans[k]$为恰保留$k$条原树边的方案数,现在改为求保留不少于$k$条边的方案数$res[k]$。
现在考虑一下在保留了$k$条边以后能产生多少棵带标号无向树(由于除了保留的边之外仍可能出现原树中的边,故求的就是$res[k]$)。这个问题就变成了Codeforces 156D,在上面有分析过,最终方案数为$n^{m-2}\cdot \prod_{i=1}^m sz[i]$,其中$m$为保留$k$条边后连通块的数量。
但是我们不可能枚举是否保留某条边,所以只能采用树形dp通过枚举连通块情况来计算方案数。记$dp[i][j][k]$表示,以$i$为当前节点、$i$所在的连通块为大小为$j$、$i$的子树内一共保留了多少条边的方案数(不包含$i$所在连通块的贡献,因为$i$可能与父亲相连构成新的连通块,决定权在父亲不在$i$),这样一来我们可以将$n^m$(暂时先求$n^{m-2}$,等到计算$res[k]$时再除$n^2$)和$\prod_{i=1}^m sz[i]$拆分到每一步,即单步只需要乘$n\times sz[son]$就可以了($i$能决定其儿子的连通块情况)。
现在考虑枚举$i$的儿子$son$和儿子的情况$jj,kk$(也就是说我们在$i$中一共枚举了$j,k,son,jj,kk$),对于每个儿子分别做背包,背包结果在$tmp[j][k]$数组中累加,计算完一个$son$后再赋回$dp[i][j][k]$。对于当前的状态,我们能决定是否主动保留$i$到$son$的这条边。如果主动保留,那么能对$tmp[j+jj][k+kk]$产生$dp[i][j][k]\times dp[son][jj][kk]$的贡献;如果不保留,那么我们就得到了一个新的连通块,其大小为$jj$,那么能对$tmp[j+jj][k+kk+1]$产生$dp[i][j][k]\times dp[son][jj][kk]\times jj\times n$的贡献。最终$res[k]=\sum_{j=1}^n dp[root][j][k]$,不过$res[n-1]=1$是特殊情况。
现在考虑得到的$res[k]$与我们真正需要求的$ans[k]$之间有什么联系。首先$ans[n-1]=res[n-1]$,然后开始扣除重复计算的情况。对于$k$,考虑$ans[j]$($j>i$)会被重复计数$\begin{pmatrix} j\\ k\end{pmatrix}$次(从$j$条边中任意选出$k$个都会被统计进$res[k]$),于是有$ans[k]=res[k]-\sum_{j=k+1}^{n-1}ans[j]$。
看起来树形dp是$O(n^5)$的,不过当背包的容量完全跟子树大小相同的时候,将$j,k$限制为之前计算过的$sz[son']$之和,将$jj,kk$限制为$sz[son]$,则可以降成$O(n^4)$,算是一个树形dp中的结论吧。(实际上看起来比$O(n^4)$小不少)
也有用矩阵树定理+插值的玩法,比较奇妙。

//0:53-1:22 #include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=105; const int mod=1000000007; inline ll quickpow(ll x,int k) { ll ans=1; while(k) { if(k&1) ans=ans*x%mod; x=x*x%mod; k>>=1; } return ans; } inline ll inv(ll x) { return quickpow(x,mod-2); } ll fac[N]; inline ll C(int x,int y) { return fac[x]*inv(fac[y])%mod*inv(fac[x-y])%mod; } int n; vector<int> v[N]; int sz[N]; ll dp[N][N][N],tmp[N][N]; void dfs(int x,int fa) { sz[x]=1; dp[x][1][0]=1; for(int y: v[x]) { if(y==fa) continue; dfs(y,x); for(int i=1;i<=sz[x]+sz[y];i++) for(int j=0;j<sz[x]+sz[y];j++) tmp[i][j]=0; for(int i=1;i<=sz[x];i++) for(int j=0;j<sz[x];j++) for(int ii=1;ii<=sz[y];ii++) for(int jj=0;jj<sz[y];jj++) { tmp[i+ii][j+jj+1]=(tmp[i+ii][j+jj+1]+dp[x][i][j]*dp[y][ii][jj])%mod; tmp[i][j+jj]=(tmp[i][j+jj]+dp[x][i][j]*dp[y][ii][jj]%mod*n*ii)%mod; } sz[x]+=sz[y]; for(int i=1;i<=sz[x];i++) for(int j=0;j<sz[x];j++) dp[x][i][j]=tmp[i][j]; } } ll res[N]; int main() { fac[0]=1; for(int i=1;i<N;i++) fac[i]=fac[i-1]*i%mod; scanf("%d",&n); for(int i=1;i<n;i++) { int x,y; scanf("%d%d",&x,&y); v[x].emplace_back(y); v[y].emplace_back(x); } dfs(1,0); for(int i=0;i<n-1;i++) for(int j=1;j<=n;j++) res[i]=(res[i]+dp[1][j][i]*inv(n)%mod*j)%mod; res[n-1]=1; for(int i=n-2;i>=0;i--) for(int j=n-1;j>i;j--) res[i]=(res[i]-res[j]*C(j,i)%mod+mod)%mod; for(int i=0;i<n;i++) printf("%lld ",res[i]); return 0; }
Luogu P5219 (无聊的水题)
还要生成函数+NTT,那就咕了
牛客 5672I (Valuable Forests,2020牛客暑期多校第七场)
可以用Cayley公式+dp推出$n$个点无根森林的结果。困难的地方在于对题目中条件的转化,以及固定两点、三点时生成树个数是通过卷积来计算的。
AtCoder arc106F (Figures)
根据题目的意思,所有的part通过connecting components相连,那么part就相当于节点,connecting component相当于边。
这样来看,原图中的$d_i$就限制了该节点在树中的度数必须在$1\leq deg_i\leq d_i$之间。
假设我们已经确定了树中每个点的度数序列为$deg_i$,考虑该度数序列可以产生多少种不同的figure。
首先根据Prufer序列的推论,一个度数序列为$deg_i$的带标号无根树的数量为$\frac{(n-2)!}{\prod_{i=1}^n (deg_i-1)!}$。再考虑第$i$个节点的$deg_i$条边可能占用hole的不同情况有$\frac{d_i!}{(d_i-deg_i)!}$种(依次给$deg_i$条边确定hole,第一条边有$n$种方案,第二条有$n-1$种,…)。于是该度数序列能够产生的figure数量为:
\[\begin{align*} &\frac{(n-2)!}{\prod_{i=1}^n (deg_i-1)!}\cdot \prod_{i=1}^n\frac{d_i!}{(n-deg_i)!}\\ =&(n-2)!\cdot \frac{d_i!}{(deg_i-1)!\cdot (d_i-deg_i)!}\\ =&(n-2)!\cdot \prod_{i=1}^n\begin{pmatrix} d_i\\ deg_i-1\end{pmatrix}\cdot d_i\end{align*}\]
由于$\prod$里面是组合数相乘的形式,所以对其考虑构造生成函数求解。
$(1+x)^{d_i}$中,$x^{deg_i}$项的系数为$\begin{pmatrix}d_i\\ deg_i\end{pmatrix}$,那么如果对其求导正是所要求的式子。于是构造的生成函数为:
\[\prod_{i=1}^n d_i\cdot (1+x)^{d_i-1}=(1+x)^{\sum_{i=1}^n d_i -n}\cdot \prod_{i=1}^n d_i\]
而我们想要的是其中第$n-2$项的系数(一个合法的度数序列应该有$\sum_{i=1}^n d_i=2(n-1)$,而由于我们对于每一项均求导,所以需要的幂次为$2(n-1)-n=n-2$),其为$\begin{pmatrix}\sum_{i=1}^n d_i-n\\ n-2\end{pmatrix}$。
将其带回原来的式子,则最终结果为:
\[\begin{align*} &(n-2)!\cdot \begin{pmatrix}\sum_{i=1}^n d_i-n\\ n-2\end{pmatrix}\\ =&(n-2)!\cdot \frac{(\sum_{i=1}^n d_i-n)!}{(n-2)!\cdot (\sum_{i=1}^n d_i-2n-2)!}\\ =&\frac{(\sum_{i=1}^n d_i-n)!}{(\sum_{i=1}^n d_i-2n-2)!}\end{align*}\]

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=200005; const int mod=998244353; int n; int d[N]; int main() { scanf("%d",&n); int sum=0,mul=1; for(int i=1;i<=n;i++) { scanf("%d",&d[i]); sum=(sum+d[i])%mod; mul=1LL*mul*d[i]%mod; } int ans=mul; for(int i=-n;i>=-2*n+3;i--) ans=1LL*ans*(sum+i+mod)%mod; printf("%d\n",ans); return 0; }
PTZ Winter Camp 2021 K7 (Colorful Components)


