整体二分
好久没写过东西了...懒狗一条。
参考了:OI Wiki - 整体二分
为了理解与实现上的方便,本文中的实现均采用vector,空间复杂度为$O(nlogn)$;而IO选手更应该采用另一种实现方法(双指针+重排序),空间复杂度为$O(n)$。不过本质上思想是一样的,只是实现上的偷懒与否。
整体二分不同于数据结构:数据结构往往是需要在线修改、在线查询(可能需要离线预处理,如离散化);而整体二分则是充分利用离线的优势,将所有的询问同时进行处理。
而其适用的范围是,每个查询的答案均具有单调性。这样说起来有点抽象,不妨直接认为是“查询区间内从小到大的第$k$个数”:如果我们二分出的中点$mid$大于答案$ans$,那么小于等于$mid$的数的数量$num$肯定大于等于$k$;如果$mid\leq ans$,那么$num\leq k$。
这说的恰恰是主席树和动态主席树的经典模板。
1. 不带修改,查询区间从小到大第$k$个数(POJ 2104,K-th Number)
先将数组$a$离散化得到数组$b$后,考虑这样处理所有的查询:
一开始,所有的询问$\{l,r,k,id\}$都被扔到了一个vector中。此时答案的范围是$1\thicksim m$($m$是离散化后不同$b_i$的数量)。
我们二分出一个中点$mid=(1+m)/2$,然后考虑将这些询问分到两个vector $vl,vr$中,其中$vl$中询问的答案小于等于$mid$、$vr$中询问的答案大于$mid$。如何检验一个询问的答案是否小于等于$mid$呢?我们可以利用树状数组,先把所有$1\leq b_i\leq mid$的$i$全部$+1$。那么对于某个具体的询问$\{l,r,k,id\}$,其答案小于等于$mid$的条件就是$[l,r]$的区间和(即区间中小于等于$mid$的数的个数)$cnt$大于等于$k$。
这样一来,对于所有的询问,我们可以分别各进行一次BIT query将其放入$vl$或$vr$中。需要注意的是,对于所有放入$vr$的询问,我们需要将它们的$k$各减去分别的$cnt$。这是因为在之后的处理中,我们仅需要计算$mid+1\thicksim m$的数有多少个出现在其包含的区间中。
以上是第一次对半划分的情况。对于一般的情况,答案区间为$[l,r]$,$mid=(l+r)/2$,我们将$l\leq b_i\leq mid$的$i$全部$+1$。其余部分均是一样的。
需要记得在每次对半划分后需要将树状数组清空。这里的清空不能用memset,而是需要进行添加的逆操作、在原来$+1$的位置$-1$。
分析一下复杂度。由于我们是对答案区间进行划分,所以划分的深度为$logn$;而由于相同深度的vector的并就是查询的全集,所以每个查询都会被划分$logn$次,而每次划分的复杂度是$(n+q)logn$(BIT query),所以整体的复杂度为$O((n+q)(logn)^2)$。
关键部分的代码:
struct Query { int l,r,k,id; }; //询问的定义 vector<int> vpos[N]; //vpos[i]包含了,所有离散化后为i的数 在a中的下标 void solve(int l,int r,vector<Query> vq) { if(l==r) //l=r则vq中的答案确定 { for(int i=0;i<vq.size();i++) ans[vq[i].id]=l; return; } int mid=(l+r)>>1; //二分中点 for(int i=l;i<=mid;i++) //将所有l<=b_i<=r的i全部+1 for(int j=0;j<vpos[i].size();j++) bit.add(vpos[i][j],1); vector<Query> vl,vr; for(int i=0;i<vq.size();i++) { Query q=vq[i]; int cnt=bit.query(q.r)-bit.query(q.l-1); //cnt为[l,r]区间中l~mid出现的次数 if(cnt>=q.k) vl.push_back(q); else q.k-=cnt,vr.push_back(Query(q)); } for(int i=l;i<=mid;i++) //清空树状数组 for(int j=0;j<vpos[i].size();j++) bit.add(vpos[i][j],-1); solve(l,mid,vl); solve(mid+1,r,vr); }
完整代码:

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; struct Query { int l,r,k,id; Query(int a=0,int b=0,int c=0,int d=0) { l=a,r=b,k=c,id=d; } }; const int N=100005; int n,m; int a[N]; int rev[N]; vector<int> v; int ans[N]; vector<int> vpos[N]; struct BIT { int t[N]; int lowbit(int x) { return x&(-x); } inline void add(int k,int x) { for(int i=k;i<=n;i+=lowbit(i)) t[i]+=x; } inline int query(int k) { int ans=0; for(int i=k;i;i-=lowbit(i)) ans+=t[i]; return ans; } }bit; void solve(int l,int r,vector<Query> vq) { if(l==r) { for(int i=0;i<vq.size();i++) ans[vq[i].id]=l; return; } int mid=(l+r)>>1; for(int i=l;i<=mid;i++) for(int j=0;j<vpos[i].size();j++) bit.add(vpos[i][j],1); vector<Query> vl,vr; for(int i=0;i<vq.size();i++) { Query q=vq[i]; int cnt=bit.query(q.r)-bit.query(q.l-1); if(cnt>=q.k) vl.push_back(q); else q.k-=cnt,vr.push_back(Query(q)); } for(int i=l;i<=mid;i++) for(int j=0;j<vpos[i].size();j++) bit.add(vpos[i][j],-1); solve(l,mid,vl); solve(mid+1,r,vr); } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&a[i]),v.push_back(a[i]); sort(v.begin(),v.end()); v.resize(unique(v.begin(),v.end())-v.begin()); for(int i=1;i<=n;i++) { int pos=lower_bound(v.begin(),v.end(),a[i])-v.begin()+1; vpos[pos].push_back(i); rev[pos]=a[i]; } vector<Query> vq; for(int i=1;i<=m;i++) { int l,r,k; scanf("%d%d%d",&l,&r,&k); vq.push_back(Query(l,r,k,i)); } solve(1,v.size(),vq); for(int i=1;i<=m;i++) printf("%d\n",rev[ans[i]]); return 0; }
2. 带修改,查询区间从小到大第$k$个数(ZOJ 2212,Dynamic Rankings)
这道题看起来就比上一题复杂了许多——毕竟用数据结构实现从主席树进化到了树套树。
不过,用整体二分仍然可以比较轻松地解决;虽然离实现还需要进行不少的分析。
首先考虑能否像上一题一样,将查询与操作分离,从而使得vector中只存放查询?答案是否定的。这是因为带修改引入了“时间”这个因素,而我们在进行$vq$到$vl,vr$的划分时会将时间打乱,因此在每次BIT query时 无法得知是否存在操作对于当前询问已经“过期”,故无法计算。
那么可以尝试将查询与操作一同放入vector中同时处理。其中,给数组$a$赋初值视为一次插入操作,进行一次单点修改视为一次删除操作后接一次插入操作。
看起来仍然无法处理“时间”因素?其实还有一些潜在的性质可以利用。由于在一开始,所有的指令均是按照时间顺序插入vector的,而且在每一层的处理都是按照vector的顺序进行,所以划分出的$vl,vr$中的指令分别按时间单调增(只不过时间不再连续)。
我们按照vector的顺序依次处理$vq$中的指令。当答案区间为$[l,r]$时,二分中点为$mid=(l+r)/2$。对于所有的询问仍然和之前一样,在树状数组上查询$[l,r]$的区间和$cnt$,并将$cnt$与$k$比较以放入$vl$或$vr$;而对于所有操作,仅在被修改值(不论是插入还是删除)小于等于$mid$时才在树状数组上修改、并放入$vl$,否则放入$vr$。
考虑一下上述做法的正确性。对于所有$l\thicksim mid$的数的贡献,假如其未被删除那么就和不带修改的情况一样,会在赋初值的那一段指令中在树状数组上$+1$;假如其会被修改,那么在被修改之前能够正确产生贡献,而在被修改时则在树状数组上$-1$,从而对之后的询问不产生贡献。这样一起处理 与 将查询和操作分离的区别,就在于能够保证按照时间处理。(如果将两者分离的话,虽然理论上也可行,但需要根据当前询问的时间 维护不同值的操作的指针,实现起来相当繁琐)
关键部分的代码:
//在表示操作时,x=下标,y=离散化值,k=插入1/删除-1,op=0,id=0 //在表示查询时,x=l,y=r,k=k,op=1,id=id struct Opt { int x,y,k,op,id; Opt(int a=0,int b=0,int c=0,int d=0,int e=0) { x=a,y=b,k=c,op=d,id=e; } }; void solve(int l,int r,vector<Opt> opt) { if(l==r) //当l=r时,opt中的所有查询操作结果均为l { for(Opt cur: opt) if(cur.op==1) ans[cur.id]=l; return; } int mid=(l+r)>>1; vector<Opt> vl,vr; for(Opt cur: opt) if(cur.op==1) //op=1,是查询指令 { int cnt=bit.query(cur.y)-bit.query(cur.x-1); if(cnt>=cur.k) vl.emplace_back(cur); else cur.k-=cnt,vr.emplace_back(cur); } else //op=0,是操作指令 if(cur.y<=mid) //当操作值小于等于mid,在树状数组上进行修改、并放入vl bit.add(cur.x,cur.k),vl.emplace_back(cur); else //否则直接放入vr vr.emplace_back(cur); for(Opt cur: opt) //树状数组清空 if(cur.op==0 && cur.y<=mid) bit.add(cur.x,-cur.k); solve(l,mid,vl); solve(mid+1,r,vr); }
完整代码:

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; struct Opt { int x,y,k,op,id; Opt(int a=0,int b=0,int c=0,int d=0,int e=0) { x=a,y=b,k=c,op=d,id=e; } }; const int N=200005; int n,m; int qcnt,ans[N]; struct BIT { int t[N]; int lowbit(int x) { return x&(-x); } inline void add(int k,int x) { for(int i=k;i<=n;i+=lowbit(i)) t[i]+=x; } inline int query(int k) { int ans=0; for(int i=k;i;i-=lowbit(i)) ans+=t[i]; return ans; } }bit; void solve(int l,int r,vector<Opt> opt) { if(l==r) { for(Opt cur: opt) if(cur.op==1) ans[cur.id]=l; return; } int mid=(l+r)>>1; vector<Opt> vl,vr; for(Opt cur: opt) if(cur.op==1) { int cnt=bit.query(cur.y)-bit.query(cur.x-1); if(cnt>=cur.k) vl.emplace_back(cur); else cur.k-=cnt,vr.emplace_back(cur); } else if(cur.y<=mid) bit.add(cur.x,cur.k),vl.emplace_back(cur); else vr.emplace_back(cur); for(Opt cur: opt) if(cur.op==0 && cur.y<=mid) bit.add(cur.x,-cur.k); solve(l,mid,vl); solve(mid+1,r,vr); } int a[N]; int op[N],x[N],y[N],k[N]; vector<int> v; inline int getpos(int x) { return lower_bound(v.begin(),v.end(),x)-v.begin()+1; } int main() { int T; scanf("%d",&T); while(T--) { qcnt=0; v.clear(); scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&a[i]),v.emplace_back(a[i]); for(int i=1;i<=m;i++) { char buf[5]; scanf("%s",buf); scanf("%d%d",&x[i],&y[i]); if(buf[0]=='Q') op[i]=1,scanf("%d",&k[i]); else op[i]=0,v.emplace_back(y[i]); } sort(v.begin(),v.end()); v.resize(unique(v.begin(),v.end())-v.begin()); vector<Opt> opt; for(int i=1;i<=n;i++) opt.emplace_back(Opt(i,getpos(a[i]),1,0,0)); for(int i=1;i<=m;i++) if(op[i]==1) opt.emplace_back(Opt(x[i],y[i],k[i],1,++qcnt)); else { opt.emplace_back(Opt(x[i],getpos(a[x[i]]),-1,0,0)); a[x[i]]=y[i]; opt.emplace_back(Opt(x[i],getpos(y[i]),1,0,0)); } solve(1,v.size(),opt); for(int i=1;i<=qcnt;i++) printf("%d\n",v[ans[i]-1]); } return 0; }
暂时感觉带修改查询的整体二分已经比较牛了,如果遇到标志性的玩法再继续补充。
整点例题。
洛谷P3242 (接水果,HNOI2015)
直接看题目还是有点麻烦的,需要进行转化。转化有两种思路:
一种是将水果的路径拎起来,在上面找子路径。也就是说,盘子的端点要分别在$lca(x,y)$到$x,y$的路径上、或者均在同一条路径上。由于任意点到根的一段路径无法简单提出,所以需要树剖后获得一段连续的dfs序。然后只能依次枚举盘子两端所在的dfs序段,从而提取出所有的盘子路径,然后线段树上二分,抽象上来说是计算矩形内的点数。时间复杂度爆炸(感觉是$O(n(logn)^3)$),细节也很多。
另一种是将盘子的路径拎起来,看能够成为多少水果路径的子路径。考虑固定盘子端点$u,v$时,水果路径的端点可能出现在哪里。记dfs整棵树时,进入$x$点的时间戳为$in[x]$、离开的时间戳为$out[x]$。那么一共只有三种情况:
1. 盘子的路径不是一条链,那么水果的端点必然分别存在于两个盘子端点的子树中
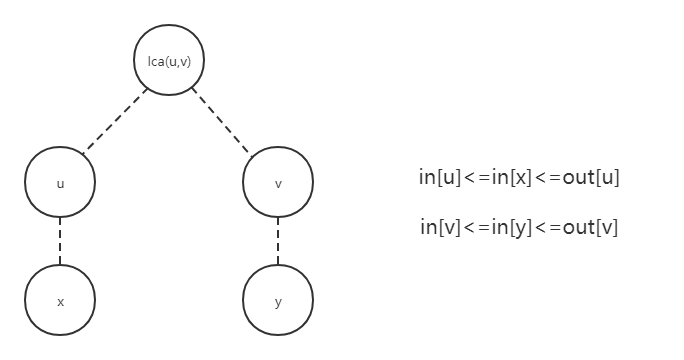
2. 盘子的路径是一条链,那么其中一个水果路径端点必然在较深盘子端点的子树中,另一个水果路径端点有两种情况

可以看出,该盘子能够接住的水果的两端点dfs序应在所确定的矩形区域内。我们不妨规定端点为$x,y$的水果的坐标为$(in[x],in[y])$(其中规定顺序为$in[x]$小于$in[y]$),那么一个盘子能够覆盖的区域为x坐标为较小dfs序范围、y坐标为较大dfs序范围 的矩形。
于是,对于每个水果(询问),就是要求能够覆盖该点的矩形中,值从小到大的第$k$个。与序列的区间相比,“覆盖”是稍微复杂一点的,不过可以考虑使用扫描线来解决。由于x/y坐标都是dfs序,所以范围都在$[1,n]$之内,那么我们考虑将每个矩形拆成上边界和下边界两个线段,如下图所示:
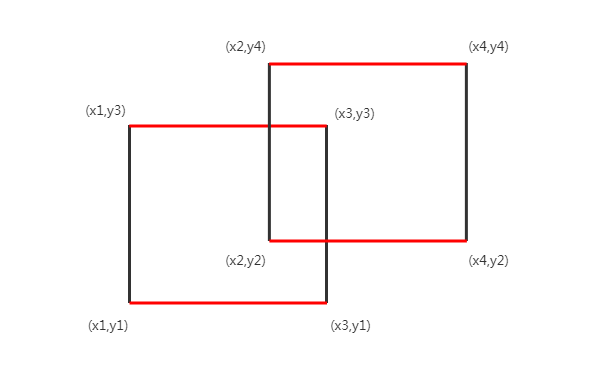
然后考虑按照y坐标从小到大的顺序开始扫描。一开始扫描到$y=y_1$,那么区间$[x_1,x_3]$均被覆盖了一遍,即是树状数组在$x_1$处$+1$、在$x_3+1$处$-1$;然后扫描到$y=y_2$,将区间$[x_2,x_4]$覆盖一遍;然后扫描到$y=y_3+1$(在$y=y_3$上的点仍然被覆盖),将区间$[x_1,x_3]$的覆盖删去,即是树状数组在$x_1$处$-1$、在$x_3+1$处$+1$;然后扫描到$y=y_4+1$,将区间$[x_1,x_3]$的覆盖删去。
我们在排序矩形的线段时,也将所有的水果的点一起按照y坐标排序。当遇到一个水果时,BIT query水果的x坐标就能得到其被覆盖的次数。其余部分就是带修改整体二分的板子了。
整体时间复杂度$O(n(logn)^2)$。

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; struct penta { int l,r,y,op,k; penta(int a=0,int b=0,int c=0,int d=0,int e=0) { l=a,r=b,y=c,op=d,k=e; } }; const int N=100005; int n,p,q; vector<int> v[N]; struct BIT { int t[N]; int lowbit(int x) { return x&(-x); } void add(int k,int x) { for(int i=k;i<=n;i+=lowbit(i)) t[i]+=x; } int query(int k) { int ans=0; for(int i=k;i;i-=lowbit(i)) ans+=t[i]; return ans; } }bit; int ans[N]; vector<penta> opt[N]; inline bool cmp(const penta &X,const penta &Y) { if(X.y!=Y.y) return X.y<Y.y; return X.op<Y.op; } //for querys: x=l, y=y, id=r, op=2, k=k //for operations: l=l, r=r, y=y, op=1 void solve(int l,int r,vector<penta> vq) { if(l==r) { for(penta cur: vq) ans[cur.r]=l; return; } int mid=(l+r)>>1; vector<penta> vl,vr; vector<penta> ord; for(int i=l;i<=mid;i++) for(penta cur: opt[i]) ord.emplace_back(cur); for(penta cur: vq) ord.emplace_back(cur); sort(ord.begin(),ord.end(),cmp); for(penta cur: ord) if(cur.op==2) { int cnt=bit.query(cur.l); if(cnt>=cur.k) vl.emplace_back(cur); else cur.k-=cnt,vr.emplace_back(cur); } else { bit.add(cur.l,cur.op); bit.add(cur.r+1,-cur.op); } for(penta cur: ord) if(cur.op<2) { bit.add(cur.l,-cur.op); bit.add(cur.r+1,cur.op); } solve(l,mid,vl); solve(mid+1,r,vr); } int to[N][16]; int tot,dep[N],in[N],out[N]; inline void dfs(int x,int fa) { to[x][0]=fa; in[x]=++tot; dep[x]=dep[fa]+1; for(int y: v[x]) if(y!=fa) dfs(y,x); out[x]=tot; } inline int lca(int x,int y) { if(dep[x]<dep[y]) swap(x,y); for(int i=15;i>=0;i--) if(dep[to[x][i]]>=dep[y]) x=to[x][i]; if(x==y) return x; for(int i=15;i>=0;i--) if(dep[to[x][i]]!=dep[to[y][i]]) x=to[x][i],y=to[y][i]; return to[x][0]; } int a[N],b[N],c[N]; int main() { scanf("%d%d%d",&n,&p,&q); for(int i=1;i<n;i++) { int x,y; scanf("%d%d",&x,&y); v[x].emplace_back(y); v[y].emplace_back(x); } dfs(1,0); for(int i=1;i<16;i++) for(int j=1;j<=n;j++) to[j][i]=to[to[j][i-1]][i-1]; vector<int> vec; for(int i=1;i<=p;i++) { scanf("%d%d%d",&a[i],&b[i],&c[i]); vec.emplace_back(c[i]); } sort(vec.begin(),vec.end()); vec.resize(unique(vec.begin(),vec.end())-vec.begin()); for(int i=1;i<=p;i++) { int x=a[i],y=b[i],w=c[i]; int pos=lower_bound(vec.begin(),vec.end(),w)-vec.begin()+1; if(in[x]>in[y]) swap(x,y); if(lca(x,y)==x) { int z=y; for(int j=15;j>=0;j--) if(dep[to[z][j]]>dep[x]) z=to[z][j]; opt[pos].emplace_back(penta(1,in[z]-1,in[y],1)); opt[pos].emplace_back(penta(1,in[z]-1,out[y]+1,-1)); if(out[z]<n) { opt[pos].emplace_back(penta(in[y],out[y],out[z]+1,1)); opt[pos].emplace_back(penta(in[y],out[y],n+1,-1)); } } else { opt[pos].emplace_back(penta(in[x],out[x],in[y],1)); opt[pos].emplace_back(penta(in[x],out[x],out[y]+1,-1)); } } vector<penta> vq; for(int i=1;i<=q;i++) { int x,y,k; scanf("%d%d%d",&x,&y,&k); if(in[x]>in[y]) swap(x,y); vq.emplace_back(penta(in[x],i,in[y],2,k)); } solve(1,vec.size(),vq); for(int i=1;i<=q;i++) printf("%d\n",vec[ans[i]-1]); return 0; }
Codeforces 484E (Sign on Fence)
离线做比在线做方便很多。看到有这么多询问,可以仔细考虑一下询问的性质。
对于一个询问$\{l,r,w\}$,我们判断其结果是否小于$x$,相当于找仅加入高度为$[x,\infty)$的栅栏时 区间$[l,r]$的最长连续段长度是否超过$w$。
在线维护区间中连续段长度是比较经典的线段树拓展应用,可以通过额外记录区间长度$len$、左延伸长度$l$、右延伸长度$r$、区间内延伸长度$x$来维护。
然后对于所有询问整体二分即可。对比前面的例题,仅仅是将判断询问的BIT换成了此处的线段树而已。

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; struct Query { int l,r,w,id; Query(int a=0,int b=0,int c=0,int d=0) { l=a,r=b,w=c,id=d; } }; struct Node { int x,len,l,r; Node() { x=len=l=r=0; } }; typedef long long ll; const int N=100005; int sz=1; Node t[N<<2]; inline void update(Node &X,const Node &L,const Node &R) { X.x=max(L.x,R.x); X.x=max(X.x,L.r+R.l); X.l=(L.l==L.len?L.len+R.l:L.l); X.r=(R.r==R.len?R.len+L.r:R.r); X.len=L.len+R.len; } void build(int k,int l,int r,int n) { if(l>n) return; if(l==r) { t[k].x=t[k].l=t[k].r=t[k].len=1; return; } int mid=(l+r)>>1; build(k<<1,l,mid,n); build(k<<1|1,mid+1,r,n); update(t[k],t[k<<1],t[k<<1|1]); } void modify(int k,int x) { k=k+sz-1; t[k].x=t[k].l=t[k].r=x; k>>=1; while(k) { update(t[k],t[k<<1],t[k<<1|1]); k>>=1; } } Node qans; void query(int k,int l,int r,int a,int b) { if(a>r || b<l) return; if(a>=l && b<=r) { update(qans,qans,t[k]); return; } int mid=(a+b)>>1; query(k<<1,l,r,a,mid); query(k<<1|1,l,r,mid+1,b); } int query(int l,int r) { qans=Node(); query(1,l,r,1,sz); return qans.x; } int n,m; int h[N]; vector<int> v; int ans[N]; vector<int> ban[N]; void solve(int l,int r,vector<Query> vq) { if(l==r) { for(Query cur: vq) ans[cur.id]=l; for(int pos: ban[l]) modify(pos,0); return; } int mid=(l+r)>>1; for(int i=l;i<=mid;i++) for(int pos: ban[i]) modify(pos,0); vector<Query> vl,vr; for(Query cur: vq) { int res=query(cur.l,cur.r); if(res>=cur.w) vr.emplace_back(cur); else vl.emplace_back(cur); } for(int i=l;i<=mid;i++) for(int pos: ban[i]) modify(pos,1); solve(l,mid,vl); solve(mid+1,r,vr); } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&h[i]),v.emplace_back(h[i]); v.emplace_back(0); sort(v.begin(),v.end()); v.resize(unique(v.begin(),v.end())-v.begin()); for(int i=1;i<=n;i++) { int pos=lower_bound(v.begin(),v.end(),h[i])-v.begin(); ban[pos].emplace_back(i); } while(sz<n) sz<<=1; build(1,1,sz,n); vector<Query> vq; scanf("%d",&m); for(int i=1;i<=m;i++) { int l,r,w; scanf("%d%d%d",&l,&r,&w); vq.emplace_back(Query(l,r,w,i)); } solve(1,(int)v.size()-1,vq); for(int i=1;i<=m;i++) printf("%d\n",v[ans[i]]); return 0; }
(完)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号