动态树(Link-Cut Tree)
之前以为很恐怖,学了之后发现没有想象中的难
关键还是长长见识,了解能够应用的方面
两个题单,慢慢刷:
目前的模板:
(UPD:2020.8.13更新,针对多测优化了一下)

const int N=300005; //在struct外遍历树上节点一定要pushdown! struct LinkCutTree { int fa[N],ch[N][2]; bool isroot[N]; int rev[N]; void init(int n) { for(int i=1;i<=n;i++) fa[i]=ch[i][0]=ch[i][1]=rev[i]=0,isroot[i]=true; } void pushdown(int x) { int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); rev[l]^=1; rev[r]^=1; rev[x]=0; } } //取决于要维护的东西 看是否要pushdown两层 void push(int x) { if(!isroot[x]) push(fa[x]); pushdown(x); } //维护Splay中的信息 void pushup(int x) { /*维护子树/连通块大小 if(x) sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+si[x]+1;*/ } void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); swap(isroot[x],isroot[f]); if(!isroot[x]) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } void splay(int x) { push(x); while(!isroot[x]) { int f=fa[x],ff=fa[f]; if(!isroot[f]) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } } //访问x 返回新根 int access(int x) { int y=0; while(x) { splay(x); //si[x]=si[x]-sz[y]+sz[ch[x][1]];//维护子树/连通块大小 isroot[ch[x][1]]=true; isroot[ch[x][1]=y]=false; pushup(y),pushup(x); y=x,x=fa[x]; } return y; } //将x置为根 void makeroot(int x) { access(x); splay(x); rev[x]^=1; } //连接x,y void link(int x,int y) { makeroot(x); //makeroot(y);//维护子树/连通块大小 fa[x]=y; //si[y]+=sz[x];//维护子树/连通块大小 pushup(y); } //断开x,y void cut(int x,int y) { makeroot(x); access(y); splay(y); fa[x]=ch[y][0]=0; isroot[x]=true; pushup(y); } //判断x,y是否相连 bool same(int x,int y) { makeroot(x); while(fa[y]) y=fa[y]; return x==y; } };
简单的目录:
题目中有一些比较重要的玩法:
维护最小生成树(也可以说维护树上路径?)
维护子树大小(指的是原树中的子树)
动态树(LCT)是一种性能很强大的数据结构,能够动态地维护一个无根森林
主要的功能包括:将两棵树合并,将一棵树分割,对于树上两点间路径进行查询/修改
在添加一个标记后,也可以维护原树中子树的大小(而不是维护splay的大小)
(虽说LCT维护的是无根森林,实际上仍然有确定的根;只是可以对于一棵树高效地换根罢了)
我们可以类比一下有根树维护路径的常用做法——树链剖分
在树链剖分中,我们将所有的边分为轻边与重边,其中重边连接而成的路径称为重链
那么需要维护的路径,就由几条轻边和重链构成,其总数是$logn$级别的;对于每条重链,分别维护链上的信息(一般是BIT/线段树)
在LCT中也有类似“重链”的设定,叫做“偏爱路径(preferred path)”;其由“偏爱边(preferred edge)”连接而成
不过,由于LCT中的树是动态的,所以偏爱路径的确立并不能像树剖一样 依赖树的结构,而是要利用“动态”的性质——也就是玄学的势能(证明可以参考 ReMoon:Splay和LCT的复杂度分析)
偏爱路径的产生,是通过LCT中的一个重要函数:$access(x)$;LCT中的所有操作都需要调用该函数
该函数的意思是,打通一条从$root$到$x$的路径,并使得这条路径成为一条偏爱路径
这其实包含两个步骤:
1. 将这条路径上的每个点原本延伸出去的偏爱边变为非偏爱边
2. 将这条路径上的边都作为偏爱边,连接成为一条偏爱路径
即如下图所示
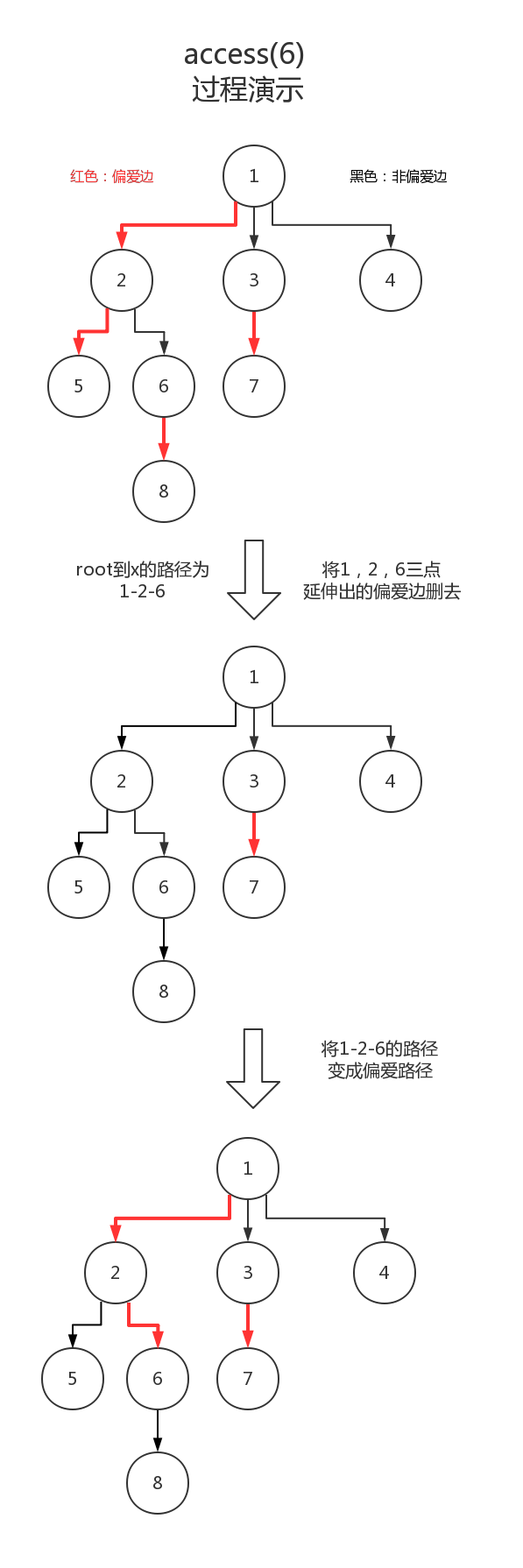
这样一来,每一条偏爱路径就是一个序列,可以考虑通过Splay来维护(因为换根需要将序列翻转)
观察上面$access(x)$的过程,可以发现当一条边$fa-x$在被设为偏爱边之前,$fa,x$两点延伸出去的偏爱边都会被删除
这表明了每一点至多会属于一条偏爱路径,跟树剖很相似,有助于我们理解LCT
然后考虑如何将偏爱路径用Splay维护
由于偏爱路径是从上层到下层的一条路径,所以不妨将路径按照从浅到深的顺序抽成一个序列
序列中的节点按照路径中的深度获得Splay中的rank,最浅的为$1$,最深的为$len$,如下图所示
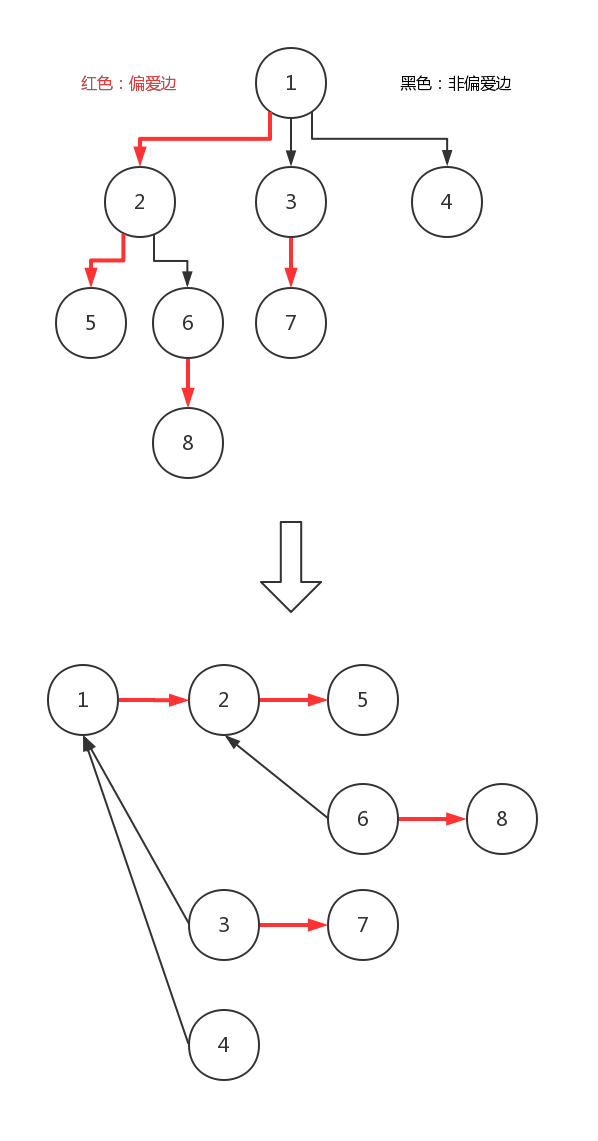
在同一Splay中的点必须在同一偏爱路径上,那么偏爱路径间的连接方式就需要考虑了
我们采用的方法是,区分一个点$x$是否为某个Splay的根节点
1. 若不是(即$fa[x]$在$x$所在的偏爱路径上),那么$fa[x]$为$x$在Splay中的父亲
2. 若是(即$fa[x]$不在$x$所在的偏爱路径上),那么$fa[x]$为$x$在原树中的父亲
需要的数组跟Splay模板中的差不多,只多了一个$isroot$
$isroot[i]$表示,$i$节点是否为某个Splay的根节点
int fa[N],ch[N][2]; bool isroot[N]; int rev[N];
先是Splay中的两个函数:$rotate(x)$和$splay(x)$
不过与Splay模板中不太一样的是,在LCT中,rotate和splay的终点是当前Splay的根节点,而不是原树的根节点
1. rotate(x)
需要记得交换$x$与$f$的$isroot$标签
void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); swap(isroot[x],isroot[f]); if(!isroot[x]) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; //pushup(f),pushup(x); }
2. splay(x)
跟Splay维护序列有些不一样的是,在LCT中没有kth函数;于是所有下传标记的任务都转移给了$splay(x)$
不过由于$splay(x)$是由下向上的过程,所以必须提前将所有标记全部下传
void pushdown(int x) { int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); rev[l]^=1,rev[r]^=1; rev[x]=0; } } void push(int x) { if(!isroot[x]) push(fa[x]); pushdown(x); } void splay(int x) { push(x); while(!isroot[x]) { int f=fa[x],ff=fa[f]; if(!isroot[f]) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } }
接着是LCT中的函数;其中$access(x)$和$makeroot(x)$都比较重要
3. access(x):访问$x$
在实际操作中,我们可以不用真的分两步执行,而可以将两步合并:
不断将当前Splay中深度较当前节点浅的并入新的Splay(即新的偏爱路径),将深度较当前节点深的割开(将偏爱边换为非偏爱边)
大概是下图的样子
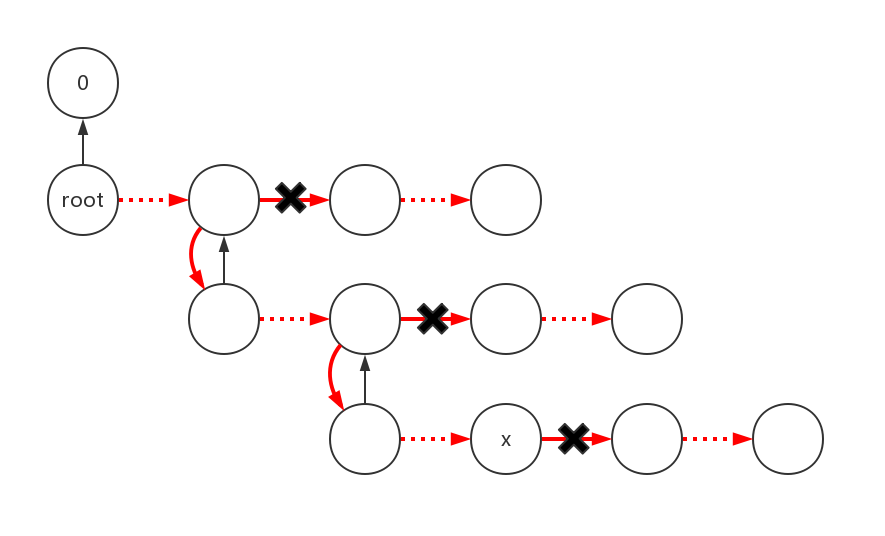
如果把当前点$x$ $splay$一下,那么$x$就成为了当前Splay的根节点
此时左子树中就都是偏爱路径中比$x$浅的节点,右子树中都是比$x$深的节点;按照需求操作即可
然后走向父节点;由于此时$x$为Splay的根节点,所以$fa[x]$为原树中的父亲
void access(int x) { int y=0;//下一层偏爱路径的根节点 while(x) { splay(x); isroot[ch[x][1]]=true; isroot[ch[x][1]=y]=false; y=x,x=fa[x]; } }
4. makeroot(x):将原树的根改为$x$
当$access(x)$之后,$x$就在偏爱路径序列的最后一个
如果我们将这个序列翻转,就能将$x$变为原树的根:
对于偏爱路径中的节点,这样显然是对的
对于不在偏爱路径中的节点,在换根后,其在原树中的父亲不变,所以也不会受到影响
void makeroot(int x) { access(x); splay(x); rev[x]^=1; }
5. link(x,y):将$x,y$分别所在的两棵树通过$x-y$的边连接起来
$makeroot(x)$以后,$x$成为了所在树的根节点
令$fa[x]=y$就可以用一条非偏爱边将两棵树连接
void link(int x,int y) { makeroot(x); fa[x]=y; }
6. cut(x,y):将$x-y$边删去,从而将一棵树分成两棵
先$makeroot(x)$,再$access(y),splay(y)$
那么此时$y$变成了原树的根,而$x$被最后一次rotate旋转到了$y$的左儿子(带着翻转标记)
于是将$y$的左儿子割下来,然后打上$isroot$标记就完成了
(其实这个函数并不能分辨原树中是否有$x-y$边,不过一般题目中不会产生这个问题)
void cut(int x,int y) { makeroot(x); access(y); splay(y); fa[x]=ch[y][0]=0; isroot[x]=true; //pushup(y); }
7. same(x,y):判断$x,y$是否在同一棵树中
先$makeroot(x)$
接着从$y$一直往上走直到根,判断一下是否为$x$(翻转标记不下传也无所谓,因为翻转标记不会改变$fa[i]$)
这个方法很多,其实怎么搞都无所谓,都是一个复杂度
bool same(int x,int y) { makeroot(x); while(fa[y]) y=fa[y]; return x==y; }
按照个人觉得逐渐加大力度的顺序出现
BZOJ 2049 (洞穴勘测,$SDOI2008$)【LCT维护连通性】
LCT模板题,只需要$link,cut,same$三种操作

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=100005; struct LinkCutTree { int fa[N],ch[N][2]; bool isroot[N]; int rev[N]; LinkCutTree() { memset(isroot,true,sizeof(isroot)); } void pushdown(int x) { int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); rev[l]^=1; rev[r]^=1; rev[x]=0; } } void push(int x) { if(!isroot[x]) push(fa[x]); pushdown(x); } void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); swap(isroot[x],isroot[f]); if(!isroot[x]) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; } void splay(int x) { push(x); while(!isroot[x]) { int f=fa[x],ff=fa[f]; if(!isroot[f]) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } } void access(int x) { int y=0; while(x) { splay(x); isroot[ch[x][1]]=true; isroot[ch[x][1]=y]=false; y=x,x=fa[x]; } } void makeroot(int x) { access(x); splay(x); rev[x]^=1; } void link(int x,int y) { makeroot(x); fa[x]=y; } void cut(int x,int y) { makeroot(x); access(y); splay(y); fa[x]=ch[y][0]=0; isroot[x]=true; } bool query(int x,int y) { makeroot(x); while(fa[y]) y=fa[y]; return x==y; } }t; int n,m; char opt[20]; int main() { scanf("%d%d",&n,&m); while(m--) { int x,y; scanf("%s%d%d",opt,&x,&y); if(opt[0]=='C') t.link(x,y); if(opt[0]=='D') t.cut(x,y); if(opt[0]=='Q') printf(t.query(x,y)?"Yes\n":"No\n"); } return 0; }
BZOJ 2002 (弹飞绵羊,$HNOI2010$)【LCT维护树的深度】
第$i$个点弹到$i+k_i$点,就相当于原树上有一条$i$到$i+k_i$的边;若$i+k_i>n$,可以指定弹到虚拟终点$n+1$
那么每次询问就是问以$n+1$为根的树中,$i$号节点的深度
由于深度就是$i$到$n+1$的距离,那么我们可以先$makeroot(n+1)$,接着$access(i)$,就把路径上的点的$sz$全部pushup到了新的根(可以修改$access(x)$函数将新的根返回)
所以我们只需要对于Splay多维护一下 子树大小$sz[i]$即可

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=200005; struct LinkCutTree { int fa[N],ch[N][2]; bool isroot[N]; int sz[N],rev[N]; LinkCutTree() { memset(isroot,true,sizeof(isroot)); } void pushdown(int x) { int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); rev[l]^=1; rev[r]^=1; rev[x]=0; } } void push(int x) { if(!isroot[x]) push(fa[x]); pushdown(x); } void pushup(int x) { if(x) sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+1; } void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); swap(isroot[x],isroot[f]); if(!isroot[x]) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } void splay(int x) { push(x); while(!isroot[x]) { int f=fa[x],ff=fa[f]; if(!isroot[f]) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } } int access(int x) { int y=0; while(x) { splay(x); isroot[ch[x][1]]=true; isroot[ch[x][1]=y]=false; pushup(y),pushup(x); y=x,x=fa[x]; } return y; } void makeroot(int x) { access(x); splay(x); rev[x]^=1; } void link(int x,int y) { makeroot(x); fa[x]=y; } void cut(int x,int y) { makeroot(x); access(y); splay(y); fa[x]=ch[y][0]=0; isroot[x]=true; pushup(y); } int depth(int root,int x) { makeroot(root); return sz[access(x)]-1; } }t; int n,m; int a[N]; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); t.link(i,min(i+a[i],n+1)); } scanf("%d",&m); while(m--) { int opt,x,y; scanf("%d%d",&opt,&x); ++x; if(opt==1) printf("%d\n",t.depth(n+1,x)); else { scanf("%d",&y); t.cut(x,min(x+a[x],n+1)); a[x]=y; t.link(x,min(x+a[x],n+1)); } } return 0; }
BZOJ 3669 (魔法森林,$NOI2014$)【LCT维护最小生成树】
这题算是集合了LCT中的几个套路
首先是two pointers:从$0$开始枚举$A$,并且对于每个$A$找到最小的$B$ 使得$1$能到达$n$;显然$B$一开始会被拉满,然后慢慢减小,整个过程是单调的
然后考虑如何对于确定的$A$找到一个最小的$B$:
将$a_i=A$的边依次尝试加入图
可能当前尝试加入的边$x-y$会和图中已有的边构成环,那么我们就找到图中$x$到$y$的路径中$b_i$最大的那条边;若此边权比当前的边权还要大,那么就将这条边删去、加入当前边
这跟构造最小生成树的过程很像;其实这道题目中我们就在用LCT维护最小生成树
在尝试加入所有$a_i=A$的边后,$1$到$n$路径上最大的$b_i$就是最小的$B$
不过在Splay中我们只能维护点权,并不能直接维护边权;一种比较方便的做法是将一条边拆成一个点和两条边
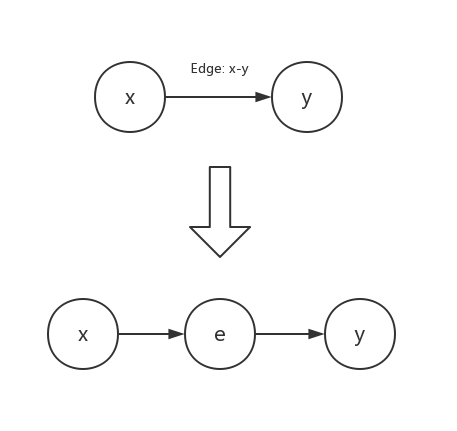
对于原图中的点,将其权值设定为不会影响答案的值(在此题中为$0$);对于边拆出的点,将其权值设定为边权
求路径上$b_i$最大的边是很容易实现的:对于每个Splay中的节点维护一下子树中权值最小的点的编号,pushup可以这样写
void pushup(int x) { int l=ch[x][0],r=ch[x][1]; mx[x]=(val[mx[l]]>val[mx[r]]?mx[l]:mx[r]); mx[x]=(val[x]>val[mx[x]]?x:mx[x]); }
对于$x$到$y$路径上的查询就可以跟上一题一样,先$makeroot(x)$,再$access(y)$,此时新根的$mx$就是路径上点权最大点的编号

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=150005; const int INF=1<<30; struct LinkCutTree { int fa[N],ch[N][2]; bool isroot[N]; int val[N],mx[N]; int rev[N]; LinkCutTree() { memset(isroot,true,sizeof(isroot)); } void pushdown(int x) { int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); rev[l]^=1; rev[r]^=1; rev[x]=0; } } void push(int x) { if(!isroot[x]) push(fa[x]); pushdown(x); } void pushup(int x) { int l=ch[x][0],r=ch[x][1]; mx[x]=(val[mx[l]]>val[mx[r]]?mx[l]:mx[r]); mx[x]=(val[x]>val[mx[x]]?x:mx[x]); } void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); swap(isroot[x],isroot[f]); if(!isroot[x]) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } void splay(int x) { push(x); while(!isroot[x]) { int f=fa[x],ff=fa[f]; if(!isroot[f]) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } } int access(int x) { int y=0; while(x) { splay(x); isroot[ch[x][1]]=true; isroot[ch[x][1]=y]=false; pushup(y),pushup(x); y=x,x=fa[x]; } return y; } void makeroot(int x) { access(x); splay(x); rev[x]^=1; } void link(int x,int y) { makeroot(x); fa[x]=y; } void cut(int x,int y) { makeroot(x); access(y); splay(y); fa[x]=ch[y][0]=0; isroot[x]=true; pushup(y); } int judge(int x,int y) { makeroot(x); int tmp=y; while(fa[tmp]) tmp=fa[tmp]; if(x==tmp) return mx[access(y)]; return -1; } }t; int n,m; int x[N],y[N],A[N],B[N]; int ord[N]; inline bool cmp(int a,int b) { return A[a]<A[b]; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { ord[i]=i; scanf("%d%d%d%d",&x[i],&y[i],&A[i],&B[i]); t.val[n+i]=B[i]; } sort(ord+1,ord+m+1,cmp); int p=1,ans=INF; for(int i=0;i<=A[ord[m]];i++) { while(p<=m && A[ord[p]]==i) { int res=t.judge(x[ord[p]],y[ord[p]]); if(res==-1) { t.link(x[ord[p]],n+ord[p]); t.link(n+ord[p],y[ord[p]]); } if(res!=-1 && B[res-n]>B[ord[p]]) { t.cut(x[res-n],res); t.cut(res,y[res-n]); t.link(x[ord[p]],n+ord[p]); t.link(n+ord[p],y[ord[p]]); } p++; } int res=t.judge(1,n); if(res!=-1) ans=min(ans,i+B[res-n]); } printf("%d\n",ans==INF?-1:ans); return 0; }
Luogu P2486 (染色,$SDOI2011$)【LCT维护序列上区间染色】
$x$到$y$的路径染色相当于$makeroot(x),access(y)$后对新根打上一个区间修改的标记
然后求序列上的不同颜色段数是一个经典问题,可以通过记录$col[i]$(当前点颜色),$lcol[i]$(区间最左端颜色),$rcol[i]$(区间最右端颜色)和$cnt[i]$(区间中颜色段数)来求解;pushup可以这样写
void pushup(int x) { if(!x) return; int l=ch[x][0],r=ch[x][1]; lcol[x]=(l?lcol[l]:col[x]); rcol[x]=(r?rcol[r]:col[x]); cnt[x]=cnt[l]+cnt[r]+1-(rcol[l]==col[x])-(lcol[r]==col[x]); }
这题中的问题在于,$cnt[i]$对于pushdown的要求很高,需要对左右儿子都pushdown后才能pushup:因为路径修改的标记下传后会影响$cnt[i]$
而对比一下弹飞绵羊和魔法森林,那两道题目中只有区间翻转标记,并且标记下传(交换左右儿子)并不会影响$sz[i],mx[i]$,所以仅需对当前节点pushdown
跟Splay序列操作中的注意事项是一样的
于是稍微修改下push函数
void push(int x) { if(!isroot[x]) push(fa[x]); else pushdown(x); pushdown(ch[x][0]),pushdown(ch[x][1]); }
然后本题中需要注意,区间翻转标记下传时要交换$lcol[x]$和$rcol[x]$

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=100005; struct LinkCutTree { int fa[N],ch[N][2]; bool isroot[N]; int col[N],lcol[N],rcol[N],cnt[N]; int rev[N],tag[N]; LinkCutTree() { memset(isroot,true,sizeof(isroot)); } void pushdown(int x) { if(!x) return; int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); swap(lcol[x],rcol[x]); rev[l]^=1,rev[r]^=1; rev[x]=0; } if(tag[x]) { col[x]=lcol[x]=rcol[x]=tag[x]; tag[l]=tag[r]=tag[x]; cnt[x]=1; tag[x]=0; } } void push(int x) { if(!isroot[x]) push(fa[x]); else pushdown(x); pushdown(ch[x][0]),pushdown(ch[x][1]); } void pushup(int x) { if(!x) return; int l=ch[x][0],r=ch[x][1]; lcol[x]=(l?lcol[l]:col[x]); rcol[x]=(r?rcol[r]:col[x]); cnt[x]=cnt[l]+cnt[r]+1-(rcol[l]==col[x])-(lcol[r]==col[x]); } void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); swap(isroot[x],isroot[f]); if(!isroot[x]) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } void splay(int x) { push(x); while(!isroot[x]) { int f=fa[x],ff=fa[f]; if(!isroot[f]) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } } int access(int x) { int y=0; while(x) { splay(x); isroot[ch[x][1]]=true; isroot[ch[x][1]=y]=false; pushup(y),pushup(x); y=x,x=fa[x]; } return y; } void makeroot(int x) { access(x); splay(x); rev[x]^=1; } void link(int x,int y) { makeroot(x); fa[x]=y; } void cut(int x,int y) { makeroot(x); access(y); splay(y); fa[x]=ch[y][0]=0; isroot[x]=true; pushup(y); } void cover(int x,int y,int w) { makeroot(x); access(y); splay(y); tag[y]=w; } }t; int n,m; char opt[5]; int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { scanf("%d",&t.col[i]); t.pushup(i); } for(int i=1;i<n;i++) { int x,y; scanf("%d%d",&x,&y); t.link(x,y); } while(m--) { int a,b,c; scanf("%s",opt); scanf("%d%d",&a,&b); if(opt[0]=='C') { scanf("%d",&c); t.cover(a,b,c); } else { t.makeroot(a); t.access(b); t.splay(b); printf("%d\n",t.cnt[b]); } } return 0; }
HDU 5333 ($Undirected\ Graph$,$2015$杭电多校)【LCT维护最大生成树+BIT】
这题是HDU 4677的数据加强版,卡了分块,其余做法都是完全一样的
也是LCT的一类套路题,大概是LCT+BIT(离线)或者LCT+主席树(强制在线)
考虑将所有询问$l_i,r_i$离线,按照$r_i$从小到大的顺序依次处理
对于当前$r=R$,将所有$y_i=R$的边(不妨令$x_i<y_i$)都尝试加入到图中,边权为$x_i$
假如将$x_i-y_i$这条边加入图后会产生一个环,那么就检查原图中$x_i$到$y_i$的这条路径;若最小的边权小于$x_i$,那么就将该边删去、加入$x_i-y_i$这条边
这样的步骤跟之前的LCT维护最小生成树有点类似,不过为什么这样是正确的呢?
因为我们会在尝试加入所有$y_i=R$的边后处理所有$r_i=R$的查询
在这种情况下,$x_i$越大的边越可能被更多的查询包含(能被$l_j\leq x_i$的查询包含),所以这样的一次替换总能够使得该连通分量对于更多的查询有贡献
于是在BIT中维护的就是边权小于等于$i$的边数;在删去一条边时,在BIT中对边权的位置$-1$,加入一条边时,在BIT中对边权的位置$+1$
而每个查询$l_i,r_i$下的共加边数就是在BIT中query($r_i$)-query($l_i$-1)

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int N=300005; const int INF=1<<30; struct LinkCutTree { int fa[N],ch[N][2]; bool isroot[N]; int val[N],mn[N]; int rev[N]; void pushdown(int x) { int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); rev[l]^=1; rev[r]^=1; rev[x]=0; } } void push(int x) { if(!isroot[x]) push(fa[x]); pushdown(x); } void pushup(int x) { int l=ch[x][0],r=ch[x][1]; mn[x]=(val[mn[l]]<val[mn[r]]?mn[l]:mn[r]); mn[x]=(val[x]<val[mn[x]]?x:mn[x]); } void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); swap(isroot[x],isroot[f]); if(!isroot[x]) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } void splay(int x) { push(x); while(!isroot[x]) { int f=fa[x],ff=fa[f]; if(!isroot[f]) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } } int access(int x) { int y=0; while(x) { splay(x); isroot[ch[x][1]]=true; isroot[ch[x][1]=y]=false; pushup(y),pushup(x); y=x,x=fa[x]; } return y; } void makeroot(int x) { access(x); splay(x); rev[x]^=1; } void link(int x,int y) { makeroot(x); fa[x]=y; } void cut(int x,int y) { makeroot(x); access(y); splay(y); fa[x]=ch[y][0]=0; isroot[x]=true; pushup(y); } int judge(int x,int y) { makeroot(x); int tmp=y; while(fa[tmp]) tmp=fa[tmp]; if(x==tmp) return mn[access(y)]; return -1; } }t; int bit[N]; inline int lowbit(int x) { return x&(-x); } inline void add(int k,int x) { for(int i=k;i<N;i+=lowbit(i)) bit[i]+=x; } inline int query(int k) { int res=0; for(int i=k;i;i-=lowbit(i)) res+=bit[i]; return res; } int n,m,q; int x[N],y[N]; vector<int> v[N]; int ql[N],qr[N]; int ord[N]; inline bool cmp(int a,int b) { return qr[a]<qr[b]; } int ans[N]; int main() { while(scanf("%d%d%d",&n,&m,&q)!=EOF) { for(int i=0;i<=n+m;i++) { bit[i]=0; t.fa[i]=t.ch[i][0]=t.ch[i][1]=t.mn[i]=t.rev[i]=0; t.val[i]=INF,t.isroot[i]=true; v[i].clear(); } for(int i=1;i<=m;i++) { scanf("%d%d",&x[i],&y[i]); if(x[i]>y[i]) swap(x[i],y[i]); v[y[i]].push_back(i); } for(int i=1;i<=q;i++) scanf("%d%d",&ql[i],&qr[i]),ord[i]=i; sort(ord+1,ord+q+1,cmp); int p=1; for(int i=1;i<=q;) { while(p<=qr[ord[i]]) { for(int j=0;j<v[p].size();j++) { int id=v[p][j]; int res=t.judge(x[id],y[id]); if(res<0) { t.val[n+id]=x[id]; t.link(x[id],n+id); t.link(n+id,y[id]); add(x[id],1); } if(res>0 && x[res-n]<x[id]) { t.cut(x[res-n],res); t.cut(res,y[res-n]); add(x[res-n],-1); t.val[n+id]=x[id]; t.link(x[id],n+id); t.link(n+id,y[id]); add(x[id],1); } } p++; } int j=i; while(j<=q && qr[ord[j]]==qr[ord[i]]) { int cur=ord[j]; ans[cur]=n-query(qr[cur])+query(ql[cur]-1); j++; } i=j; } for(int i=1;i<=q;i++) printf("%d\n",ans[i]); } return 0; }
CF Gym 100543J ($Pork\ barrel$,$CERC14$)【LCT+主席树】
待补
BZOJ 4530 (大融合,$BJOI2014$)【LCT维护子树大小】
裸的LCT是无法维护子树大小的
在上面的弹飞绵羊中,维护的“子树大小”指的是Splay的大小,其实是“偏爱路径长度”
所以我们的困难之处在于,我们在当前节点仅有Splay的信息,而虚儿子的贡献无法被统计到
于是用$si[i]$记录$i$所有虚儿子的子树大小之和,而$sz[i]$表示$i$的子树大小
那么显然有$si[i]=\sum_{\text{j为i的虚儿子}}sz[j]$,$sz[i]=sz[ch[i][0]]+sz[ch[i][1]]+si[i]+1$
其中$sz[i]$可以在pushup中很方便地维护,但是$si[i]$却并不能这样做;需要考虑什么操作会带来$si[i]$的改变
其实只有两处:
在access的时候,会将一些节点由实儿子变为虚儿子、虚儿子变为实儿子
在link的时候,会由一个节点向另一个节点连一条虚边
于是在两个地方分别修改
int access(int x) { int y=0; while(x) { splay(x); si[x]=si[x]-sz[y]+sz[ch[x][1]];//新添的语句 isroot[ch[x][1]]=true; isroot[ch[x][1]=y]=false; pushup(y),pushup(x); y=x,x=fa[x]; } return y; }
void link(int x,int y) { makeroot(x); makeroot(y);//新添的语句 fa[x]=y; si[y]+=sz[x];//新添的语句 pushup(y); }
为什么要在link中多加一句makeroot(y)呢?因为我们每次仅能更新一个节点的$si[i]$,并不能上传,所以一定要让$y$成为其所在Splay的根
而在access中,由于先有了splay(x),所以$x$一定是根,无需再makeroot
不过,想要得到正确的$sz[i]$,还需要注意一点:由于$i$在Splay中的左右儿子都会对$sz[i]$产生贡献,所以需要让$i$的Splay中的前驱成为根、让$i$成为根的右儿子,这样一来就把所有比$i$深的点全部夹到$i$在Splay的儿子中了
这就是为什么在代码中要makeroot(x),makeroot(y);这样一来$y$为根、$x$为左儿子(且$x$无实儿子),与上面所说的夹法是等价的

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int N=200005; struct LinkCutTree { int fa[N],ch[N][2]; bool isroot[N]; int rev[N],sz[N],si[N]; LinkCutTree() { memset(isroot,true,sizeof(isroot)); } void pushdown(int x) { int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); rev[l]^=1; rev[r]^=1; rev[x]=0; } } //取决于要维护的东西 看是否要pushdown两层 void push(int x) { if(!isroot[x]) push(fa[x]); pushdown(x); } //维护Splay中的信息 void pushup(int x) { if(x) sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+si[x]+1; } void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); swap(isroot[x],isroot[f]); if(!isroot[x]) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } void splay(int x) { push(x); while(!isroot[x]) { int f=fa[x],ff=fa[f]; if(!isroot[f]) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } } //访问x 返回新根 int access(int x) { int y=0; while(x) { splay(x); si[x]=si[x]-sz[y]+sz[ch[x][1]]; isroot[ch[x][1]]=true; isroot[ch[x][1]=y]=false; pushup(y),pushup(x); y=x,x=fa[x]; } return y; } //将x置为根 void makeroot(int x) { access(x); splay(x); rev[x]^=1; } //连接x,y void link(int x,int y) { makeroot(x); makeroot(y); fa[x]=y; si[y]+=sz[x],pushup(y); } }t; int n,m; int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) t.sz[i]=1,t.si[i]=0; t.sz[0]=t.si[0]=0; while(m--) { char opt=getchar(); while(opt<'A' || opt>'Z') opt=getchar(); int x,y; scanf("%d%d",&x,&y); if(opt=='A') t.link(x,y); else { t.makeroot(x); t.makeroot(y); printf("%lld\n",1LL*t.sz[x]*(t.sz[y]-t.sz[x])); } } return 0; }
BZOJ 3510 (首都)【LCT维护重心】(维护子树大小+重心性质+启发式合并)
在struct外遍历树上节点一定要pushdown!
在struct外遍历树上节点一定要pushdown!
在struct外遍历树上节点一定要pushdown!
首先题目中“到各点距离之和最小”就是重心的一个定义,然后这题需要利用重心的几个性质:
1. 把重心作为根,则最大子树大小不超过$\frac{n}{2}$
2. 把两棵树通过一条边相连,则新树的重心在原来两树重心的连线上(即使原来的树有$2$个重心仍然成立)
3. 若在一棵树上再连接一个节点,那么重心最多会移动$1$的距离
于是用LCT维护树的结构,并且不断将重心makeroot;在LCT外,用并查集维护重心(也可以在LCT上查找,就是慢了些)
每次合并两棵树,就在两棵树重心的连线上找到所有子树大小不超过$\frac{n}{2}$的点即可;只要检查 原来两棵树重心 分别所在的子树就可以了(其他子树一定不会比这两个大)
不过这一条链可能相当长,在极端情况下,重心到叶子节点的距离可能是$\frac{n}{2}$;所以需要考虑优化
使用启发式合并:将较小的树并到较大的树上,那么重心移动(从较大树的重心开始)的最大距离 就是较小树的大小,整体上是$O(nlogn)$的
好像大部分的题解思路是将较小树的节点拆下来一个个连上去、每次看要不要移动;不过我的做法是,在LCT中link后通过access将这条链提出来,然后在这条链对应的Splay上找后继,由于是依次访问所以复杂度为$O(n)$
找后继的时候要注意pushdown...在这里卡了三天(丢人)

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int N=200005; struct LinkCutTree { int fa[N],ch[N][2]; bool isroot[N]; int rev[N],sz[N],si[N]; LinkCutTree() { memset(isroot,true,sizeof(isroot)); } void pushdown(int x) { int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); rev[l]^=1; rev[r]^=1; rev[x]=0; } } //取决于要维护的东西 看是否要pushdown两层 void push(int x) { if(!isroot[x]) push(fa[x]); pushdown(x); } //维护Splay中的信息 void pushup(int x) { //维护子树/连通块大小 if(x) sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+si[x]+1; } void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); swap(isroot[x],isroot[f]); if(!isroot[x]) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } void splay(int x) { push(x); while(!isroot[x]) { int f=fa[x],ff=fa[f]; if(!isroot[f]) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } } //访问x 返回新根 int access(int x) { int y=0; while(x) { splay(x); si[x]=si[x]-sz[y]+sz[ch[x][1]]; //维护子树/连通块大小 isroot[ch[x][1]]=true; isroot[ch[x][1]=y]=false; pushup(y),pushup(x); y=x,x=fa[x]; } return y; } //将x置为根 void makeroot(int x) { access(x); splay(x); rev[x]^=1; } //连接x,y void link(int x,int y) { makeroot(x); makeroot(y);//维护子树/连通块大小 fa[x]=y; si[y]+=sz[x],pushup(y);//维护子树/连通块大小 } //断开x,y void cut(int x,int y) { makeroot(x); access(y); splay(y); fa[x]=ch[y][0]=0; isroot[x]=true; pushup(y); } }; int n,m,xorsum; char opt[5]; int fa[N]; LinkCutTree t; inline int find(int x) { if(fa[x]==x) return x; return fa[x]=find(fa[x]); } inline int next(int x) { t.splay(x); t.pushdown(x); if(!t.ch[x][1]) return -1; int y=t.ch[x][1]; t.pushdown(y); while(t.ch[y][0]) y=t.ch[y][0],t.pushdown(y); return y; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) xorsum^=i,t.sz[i]=1,fa[i]=i; while(m--) { int x,y; scanf("%s",opt); if(opt[0]=='A') { scanf("%d%d",&x,&y); int rx=find(x),ry=find(y); int nroot=0,tsz=t.sz[rx]+t.sz[ry]; if(t.sz[rx]<t.sz[ry]) swap(x,y),swap(rx,ry); t.link(y,x); t.makeroot(rx); t.access(ry),t.splay(rx); int cnt=1; int cur=rx,nxt=next(cur),last=rx; t.splay(nxt),t.splay(cur); while(t.sz[nxt]*2>tsz) { last=cur,cur=nxt,nxt=next(cur); t.splay(nxt),t.splay(cur); cnt++; } t.splay(cur),t.splay(last); while((tsz-t.sz[cur])*2<=tsz) { cnt++; if(!nroot || nroot>cur) nroot=cur; last=cur,cur=next(cur); if(cur==-1) break; t.splay(cur),t.splay(last); } t.makeroot(nroot); fa[nroot]=fa[rx]=fa[ry]=nroot; xorsum^=rx^ry^nroot; } if(opt[0]=='Q') { scanf("%d",&x); printf("%d\n",find(x)); } if(opt[0]=='X') printf("%d\n",xorsum); } return 0; }
牛客38727C Cmostp(2022 牛客暑期多校 加赛)【SAM,LCT access 维护 parent 树的链并,离线转化】
首先从字符串转化为树上问题:右端点在区间 $[l,r]$ 的状态等价于字符串 $s[1:l]$ 到 $s[1:r]$ 这 $r-l+1$ 个状态在 SAM parent 树上的链并。
接着考虑使用扫描线,从左向右扫描 $r$,对于每个 $r$ 回答依次回答所有 $[l_i,r]$ 的询问。为了能够维护这样的信息,我们在 parent 树上暴力染色,并通过树状数组维护每个标记的子串数量,规则为:使用 LCT 对于 $s[1:r]$ 所属的状态进行 access,那么我们会得到一条偏爱路径、并在这个过程中拆分一些原有的偏爱路径。我们将新得到的偏爱路径暴力染上标记 $r$,同时在树状数组的位置 $r$ 加上该偏爱路径的表示的子串数量;对于被拆分的原有的偏爱路径,我们在对应标记的位置减去被拆分出的子串数量。那么对于询问 $[l_i,r]$ 就是在树状数组上对 $[l_i,r]$ 的区间求和。
每个节点的标记可以通过懒标记维护,在 splay 的时候 pushdown 下去即可。另外,同一标记的点一定属于同一个 splay,故其数量等价于 splay 的大小,可以通过 pushup 维护。暴力染色的复杂度等同于 access 的复杂度,是 $\mathrm{O}(n\ logn)$ 的。考虑到每次暴力染色还需要进行树状数组修改,所以最终整体复杂度为 $\mathrm{O}(n\ logn^2)$。

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef pair<int,int> pii; const int N=500005; ll t[N]; inline int lowbit(int x) { return x&(-x); } inline void add(int k,int x) { if(!k) return; for(int i=k;i<N;i+=lowbit(i)) t[i]+=x; } inline ll sum(int k) { ll ans=0; for(int i=k;i;i-=lowbit(i)) ans+=t[i]; return ans; } bool isroot[N<<1]; int fa[N<<1],ch[N<<1][2]; int sz[N<<1],len[N<<1],col[N<<1],tag[N<<1]; void clear(int n) { for(int i=1;i<=n;i++) fa[i]=ch[i][0]=ch[i][1]=0,sz[i]=1,isroot[i]=true; } void pushup(int x) { if(x) sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+len[x]; } void pushdown(int x) { if(tag[x]) { tag[ch[x][0]]=tag[ch[x][1]]=tag[x]; col[x]=tag[x],tag[x]=0; } } void push(int x) { if(!isroot[x]) push(fa[x]); pushdown(x); } void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); swap(isroot[x],isroot[f]); if(!isroot[x]) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } void splay(int x) { push(x); while(!isroot[x]) { int f=fa[x],ff=fa[f]; if(!isroot[f]) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } } int access(int x,int val) { int y=0; while(x) { splay(x); add(col[x],sz[ch[x][1]]-sz[x]); add(val,sz[x]-sz[ch[x][1]]); isroot[ch[x][1]]=true; isroot[ch[x][1]=y]=false; tag[x]=val; pushup(y),pushup(x); y=x,x=fa[x]; } return y; } const int C=26; //注意检查字符集大小! //在结构题外开任何与SAM状态相关的数组,都需要N<<1 struct SuffixAutomaton { int sz,lst; //状态数上限=2|S|-1 int len[N<<1],link[N<<1]; int nxt[N<<1][C]; //map<char,int> nxt[N<<1]; //extend(char),并使用nxt[clone]=nxt[q]替换memcpy SuffixAutomaton() { len[0]=0,link[0]=-1; lst=sz=0; } void extend(int c) { int cur=++sz; len[cur]=len[lst]+1; int p=lst; while(p!=-1 && !nxt[p][c]) nxt[p][c]=cur,p=link[p]; if(p==-1) link[cur]=0; else { int q=nxt[p][c]; if(len[p]+1==len[q]) link[cur]=q; else { int clone=++sz; len[clone]=len[p]+1; link[clone]=link[q]; memcpy(nxt[clone],nxt[q],C*4); while(p!=-1 && nxt[p][c]==q) nxt[p][c]=clone,p=link[p]; link[q]=link[cur]=clone; } } lst=cur; } }sam; int n,q; char s[N]; vector<pii> vq[N]; ll ans[N]; int main() { scanf("%d%d",&n,&q); scanf("%s",s+1); for(int i=1;i<=q;i++) { int x,y; scanf("%d%d",&x,&y); vq[y].emplace_back(pii(x,i)); } for(int i=1;i<=n;i++) sam.extend(s[i]-'a'); clear(sam.sz); for(int i=1;i<=sam.sz;i++) fa[i]=sam.link[i], sz[i]=len[i]=sam.len[i]-sam.len[sam.link[i]]; for(int i=1,cur=0;i<=n;i++) { cur=sam.nxt[cur][s[i]-'a']; access(cur,i); for(pii x: vq[i]) ans[x.second]=sum(n)-sum(x.first-1); } for(int i=1;i<=q;i++) printf("%lld\n",ans[i]); return 0; }
~ 一些训练遇到的杂题 ~
HDU 6858 (Discovery of Cycles,2020 Multi-University Training Contest 8)
如果能看出来成环区间能够用two pointers依次求,就是一个简单的LCT维护树上连通性了。
牛客 204603 (Graph,2019ICPC沈阳)
这题没有让求有多少个点对连通,而是问是否全部连通,所以可以反向揣测出来只能求整体的状态。
而求整体是否连通可以用xor:给点对$(u,v)$上的两点均赋上随机点权,若两者连通则该连通块xor值为$0$,否则至少有一个连通块xor值不为$0$。
连通块的xor值可以考虑类似子树大小维护,改一下sz、si的意义即可。

#include <map> #include <random> #include <chrono> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef pair<int,int> pii; typedef unsigned int ui; const int N=100005; mt19937 mt_rand(chrono::high_resolution_clock::now().time_since_epoch().count()); int num; //在struct外遍历树上节点一定要pushdown! struct LinkCutTree { int fa[N],ch[N][2]; bool isroot[N]; int rev[N]; ui sz[N],si[N],val[N]; void init(int n) { for(int i=1;i<=n;i++) fa[i]=ch[i][0]=ch[i][1]=rev[i]=sz[i]=si[i]=val[i]=0,isroot[i]=true; } void pushdown(int x) { int &l=ch[x][0],&r=ch[x][1]; if(rev[x]) { swap(l,r); rev[l]^=1; rev[r]^=1; rev[x]=0; } } //取决于要维护的东西 看是否要pushdown两层 void push(int x) { if(!isroot[x]) push(fa[x]); pushdown(x); } //维护Splay中的信息 void pushup(int x) { /*维护子树/连通块大小*/ if(x) sz[x]=sz[ch[x][0]]^sz[ch[x][1]]^si[x]^val[x]; } void rotate(int x) { int f=fa[x],ff=fa[f]; int dir=(ch[f][1]==x); swap(isroot[x],isroot[f]); if(!isroot[x]) ch[ff][ch[ff][1]==f]=x; fa[x]=ff; ch[f][dir]=ch[x][dir^1]; fa[ch[x][dir^1]]=f; ch[x][dir^1]=f; fa[f]=x; pushup(f),pushup(x); } void splay(int x) { push(x); while(!isroot[x]) { int f=fa[x],ff=fa[f]; if(!isroot[f]) rotate((ch[f][1]==x)==(ch[ff][1]==f)?f:x); rotate(x); } } //访问x 返回新根 int access(int x) { int y=0; while(x) { splay(x); si[x]=si[x]^sz[y]^sz[ch[x][1]];//维护子树/连通块大小 isroot[ch[x][1]]=true; isroot[ch[x][1]=y]=false; pushup(y),pushup(x); y=x,x=fa[x]; } return y; } //将x置为根 void makeroot(int x) { access(x); splay(x); rev[x]^=1; } //连接x,y void link(int x,int y) { makeroot(x); if(sz[x]!=0) num--; makeroot(y);//维护子树/连通块大小 if(sz[y]!=0) num--; fa[x]=y; si[y]^=sz[x];//维护子树/连通块大小 pushup(y); if(sz[y]!=0) num++; } //断开x,y void cut(int x,int y) { makeroot(x); if(sz[x]!=0) num--; access(y); splay(y); fa[x]=ch[y][0]=0; isroot[x]=true; pushup(y); if(sz[x]!=0) num++; if(sz[y]!=0) num++; } //判断x,y是否相连 bool same(int x,int y) { makeroot(x); while(fa[y]) y=fa[y]; return x==y; } void change(int x,ui w) { makeroot(x); if(sz[x]!=0) num--; val[x]^=w; pushup(x); if(sz[x]!=0) num++; } }t; int n,m; int main() { int T; scanf("%d",&T); while(T--) { scanf("%d%d",&n,&m); t.init(n),num=0; map<pii,ui> mp; while(m--) { int opt,x,y; scanf("%d",&opt); if(opt!=5) { scanf("%d%d",&x,&y); if(x>y) swap(x,y); } if(opt==1) t.link(x,y); if(opt==2) t.cut(x,y); if(opt==3) { ui rnd=mt_rand(); mp[pii(x,y)]=rnd; t.change(x,rnd); t.change(y,rnd); } if(opt==4) { ui rnd=mp[pii(x,y)]; t.change(x,rnd); t.change(y,rnd); } if(opt==5) printf(num==0?"YES\n":"NO\n"); } } return 0; }
(待续)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号