左偏树
有点特定的知识点,不过还是需要补的
模板:
(UPD:2020.3.20增加一句提示)

int ls[N],rs[N]; int val[N],dis[N],fa[N];//建议令val[0]=-1 记得给fa赋初值 //将根为x,y的两个堆合并 返回合并后的根 int merge(int x,int y) { if(!x || !y) return x+y; //此处为小根堆 if(val[x]>val[y]) swap(x,y); int &L=ls[x],&R=rs[x]; R=merge(R,y); fa[R]=x; if(dis[L]<dis[R]) swap(L,R); dis[x]=dis[R]+1; return x; } //将根为x的堆弹出堆顶 void pop(int x) { val[x]=-1; fa[ls[x]]=ls[x],fa[rs[x]]=rs[x]; fa[x]=merge(ls[x],rs[x]); } int find(int a) { if(fa[a]==a) return a; return fa[a]=find(fa[a]); }
~ 简介 ~
支持快速合并的堆;单次合并复杂度$O(logn)$
~ 左偏 ~
堆的性质就不加赘述了,但是左偏的性质还是有点意思的
左偏指的是:对于每个节点,都保证 其左儿子到叶节点的最短距离 大于等于 其右儿子到叶节点的最短距离
这能保证一个性质:从根节点一直向右走到叶节点的这条链,长度是不超过$logn$的
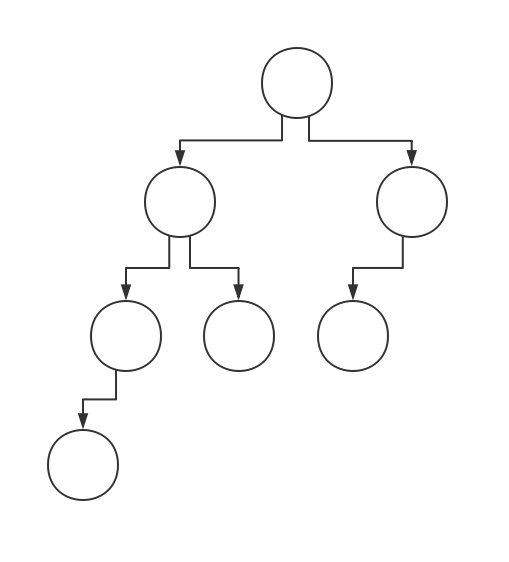
证明比较显然:若要保证树左偏,那么将树按照最右链的深度横着切一刀,应该是一棵满二叉树,则总节点数不少于$2^{\text{最右链长度}}$,从而最右链长度为$logn$级别的
不过需要注意,左偏树并不能保证树的高度是$logn$级别的,最左链可以达到$n$级别的深度
~ 合并 ~
最右链的深度为$logn$的性质有助于我们将两棵左偏树合并
我们考虑每次将两个树的根相比(默认位小根堆),将较小的那个置为合并后的根;然后将另一个根递归下去,与较小根的右儿子进行比较
一直这样比下去,那么在过程中可能选为子树根的的元素只有可能出现在原来两树的最右链上,而这两个最右链上的元素是$logn$级别的,故总时间复杂度为$O(logn)$
不过这样一次合并后的树不一定满足左偏的性质了,故在回溯的过程中要对合并后的树进行调整
调整的过程不复杂:若左儿子到叶节点的最短距离 小于 右儿子到叶节点的最短距离,交换左右儿子即可
//将根为x,y的两个堆合并 返回合并后的根 int merge(int x,int y) { if(!x || !y) return x+y; //此处为小根堆 if(val[x]>val[y]) swap(x,y); int &L=ls[x],&R=rs[x]; R=merge(R,y); fa[R]=x;//fa的作用后面会涉及 if(dis[L]<dis[R]) swap(L,R); dis[x]=dis[R]+1; return x; }
利用merge函数,也可以轻松的完成插入与弹出
插入比较简单,将待插入节点初始化、赋值后merge到希望插入的堆中就行了
弹出堆顶,将根的左右儿子合并即可
//将根为x的堆弹出堆顶 void pop(int x) { val[x]=-1; fa[ls[x]]=ls[x],fa[rs[x]]=rs[x]; fa[x]=merge(ls[x],rs[x]); }
在上面的merge与pop函数中都出现了$fa$数组,它有什么意义呢?
如果简简单单将两棵左偏树合并,那么我们并不能维护每个元素在合并后处于哪一棵树中
所以可以考虑用树的根来作为处于哪一棵树中的判断依据:如果两个节点所在树的根相同,它们显然在同一棵树中
这个合并、维护根的过程,很容易让我们联想到一种简单高效的数据结构——并查集
$fa[i]$表示节点$i$的父亲,一直往父亲走就可以知道根是哪个了
不过,左偏的性质仅仅能保证最右链的深度不会很大,整棵树中仍有可能存在很深的节点:一棵一直向左延伸的树也满足左偏的要求
所以我们不能满足于暴力向上爬,必须使用其它技巧
首先想到的就是路径压缩
不过我们在pop函数中,需要将一个元素从堆中弹出,这是否会影响路径压缩的正确性呢?因为正常的路径压缩是不能删边的
其实不会
我们弹出一个元素,是让它不能通过$ls,rs$来向下访问其儿子,但这并不意味着我们不能继续利用它的$fa$:我们可以将这个元素当做一个虚拟节点
假设在弹出堆顶以后,左儿子将作为新的根,那么我们将被弹出元素的$fa$指向左儿子,这显然会让指向原来堆顶的元素转而最终指向左儿子,并不会带来任何问题
不过在pop函数中需要先将两个儿子的$fa$都设成自己
(在pop调用的merge之中,会将合并后非根节点的$fa$指向新根,再加上虚拟节点的帮助,所有节点最终都能指向新根)
int find(int a) { if(fa[a]==a) return a; return fa[a]=find(fa[a]); }
~ 例题 ~
Luogu P3377 (【模板】左偏树(可并堆))
需要利用$fa$来判断每个数属于哪个堆,$val[i]=-1$表示已被删除

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=100005; int ls[N],rs[N]; int val[N],dis[N],fa[N]; //将根为x,y的两个堆合并 返回合并后的根 int merge(int x,int y) { if(!x || !y) return x+y; //此处为小根堆 if(val[x]>val[y]) swap(x,y); int &L=ls[x],&R=rs[x]; R=merge(R,y); fa[R]=x; if(dis[L]<dis[R]) swap(L,R); dis[x]=dis[R]+1; return x; } //将根为x的堆弹出堆顶 void pop(int x) { val[x]=-1; fa[ls[x]]=ls[x],fa[rs[x]]=rs[x]; fa[x]=merge(ls[x],rs[x]); } int find(int a) { if(fa[a]==a) return a; return fa[a]=find(fa[a]); } int n,m; int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&val[i]),fa[i]=i; while(m--) { int opt,x,y; scanf("%d%d",&opt,&x); if(opt==1) { scanf("%d",&y); if(val[x]<0 || val[y]<0) continue; x=find(x),y=find(y); if(x!=y) merge(x,y); } else { if(val[x]>0) x=find(x); printf("%d\n",val[x]); if(val[x]>0) pop(x); } } return 0; }
Luogu P1152 (派遣,$APIO2012$)
显然可以尝试让每个忍者都成为管理者,那么问题就转化成了求一个子树内最多能选出多少个人
最优的情况是选出子树中薪水最少的人
那么我们就需要动态地维护薪水最少、且总薪水不超过$m$的节点的集合;这可以通过大根堆来实现
对于当前节点,我们将其儿子的堆都合并上去,那么总薪水可能就超过$m$了,于是不停地将最大的节点弹出、直到总薪水小于等于$m$就可以了

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=100005; int ls[N],rs[N]; int val[N],dis[N],fa[N]; //将根为x,y的两个堆合并 返回合并后的根 int merge(int x,int y) { if(!x || !y) return x+y; //此处为大根堆 if(val[x]<val[y]) swap(x,y); int &L=ls[x],&R=rs[x]; R=merge(R,y); fa[R]=x; if(dis[L]<dis[R]) swap(L,R); dis[x]=dis[R]+1; return x; } //将根为x的堆弹出堆顶 void pop(int x) { val[x]=-1; fa[ls[x]]=ls[x],fa[rs[x]]=rs[x]; fa[x]=merge(ls[x],rs[x]); } int find(int a) { if(fa[a]==a) return a; return fa[a]=find(fa[a]); } int n,m,root; int mul[N],num[N],sum[N]; vector<int> v[N]; ll ans; void dfs(int x) { for(int i=0;i<v[x].size();i++) { int y=v[x][i]; dfs(y); merge(find(x),find(y)); num[x]+=num[y]; sum[x]+=sum[y]; while(sum[x]>m) { sum[x]-=val[find(x)]; num[x]--; pop(find(x)); } } ans=max(ans,1LL*mul[x]*num[x]); } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { int x; scanf("%d%d%d",&x,&val[i],&mul[i]); fa[i]=i,num[i]=1,sum[i]=val[i]; if(!x) root=i; else v[x].push_back(i); } dfs(root); printf("%lld\n",ans); return 0; }
HDU 5575 ($Discover\ Water\ Tank$,$2015ICPC$上海)
之前用的是笛卡尔树+倍增,确实比左偏树麻烦太多...
我们按照隔板高度从小到大来合并相邻两个区间,并计算不灌满/灌满该区间(灌满指的是灌到隔板的高度)所能满足的最多query数$dp[i][0],dp[i][1]$
转移比较显然:$dp[i][0]=dp[L][0]+dp[R][0]$,$dp[i][1]=dp[L][1]+dp[R][1]$
考虑在一开始将所有的query扔到所在的格子中,那么一开始只有$z=0$的query被满足
对于枚举出的隔板,我们考虑对左右两侧分别灌水,初始的当前满足query数$cur=dp[i][1]$(若子区间没被灌满就不能继续灌水了),若遇到一个$z=0$的查询就让$cur--$,否则$cur++$;不停的用$cur$来更新答案
需要注意的一个细节是,对于$y$相同的query,需要将$z=0$的放在前面;因为按理说这些query需要同时被处理,但是我们先处理$z=0$的并不会影响答案的正确性,但若先处理$z=1$的可能会使$cur$变得过大
维护隔板隔开的区间需要再整一个并查集
这题中,为了确定某一个格子对应的是哪一个左偏树,我的做法是先给每个格子一个节点,$val$赋为$INF$,再将query跟这些节点合并;这样处理就不用什么特判了

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=300005; const int INF=1<<30; int tot,ls[N],rs[N]; int val[N],tag[N],dis[N],fa[N]; //将根为x,y的两个堆合并 返回合并后的根 int merge(int x,int y) { if(!x || !y) return x+y; //此处为小根堆 if(val[x]>val[y] || (val[x]==val[y] && tag[x]>tag[y])) swap(x,y); int &L=ls[x],&R=rs[x]; R=merge(R,y); fa[R]=x; if(dis[L]<dis[R]) swap(L,R); dis[x]=dis[R]+1; return x; } //将根为x的堆弹出堆顶 void pop(int x) { val[x]=-1; fa[ls[x]]=ls[x],fa[rs[x]]=rs[x]; fa[x]=merge(ls[x],rs[x]); } int find(int a) { if(fa[a]==a) return a; return fa[a]=find(fa[a]); } int n,m; int h[N],ord[N]; inline bool cmp(int x,int y) { return h[x]<h[y]; } int lmost[N],dp[N][2]; int Find(int x) { if(lmost[x]==x) return x; return lmost[x]=Find(lmost[x]); } void solve(int x,int lim) { int cur=dp[x][1],tmp=max(dp[x][0],dp[x][1]); while(val[find(x)]<=lim) { cur+=tag[find(x)]; tmp=max(tmp,cur); pop(find(x)); } dp[x][0]=tmp,dp[x][1]=cur; } int main() { int T; scanf("%d",&T); for(int kase=1;kase<=T;kase++) { for(int i=1;i<=n+m;i++) ls[i]=rs[i]=0; scanf("%d%d",&n,&m); tot=n; for(int i=1;i<=n;i++) { val[i]=INF; lmost[i]=fa[i]=i; dp[i][0]=dp[i][1]=0; } for(int i=1;i<n;i++) { scanf("%d",&h[i]); ord[i]=i; } for(int i=1;i<=m;i++) { int x,y,z; scanf("%d%d%d",&x,&y,&z); ++tot; dp[x][1]+=1-z; val[tot]=++y,tag[tot]=(!z?-1:1),fa[tot]=tot; merge(find(x),tot); } sort(ord+1,ord+n,cmp); for(int i=1;i<n;i++) { int id=ord[i]; int L=Find(id),R=id+1; solve(L,h[id]),solve(R,h[id]); dp[L][0]+=dp[R][0]; dp[L][1]+=dp[R][1]; merge(find(L),find(R)); lmost[R]=L; } solve(1,INF-1); printf("Case #%d: %d\n",kase,dp[1][0]); } return 0; }
个人感觉是不太容易碰到...?
竟然难得遇到一个:OpenTrain 010475J
($XX\ Open\ Cup\ named\ after\ E.V.\ Pankratiev.\ Grand\ Prix\ of\ Korea$)

Problem J. Parklife Input file: standard input Output file: standard output Time limit: 1.5 seconds Memory limit: 1024 mebibytes Gapcheon is a stream that flows through the Daedeok Innopolis: A research district in Daejeon which includes KAIST, Expo Science Park, National Science Museum, among many others. The waterfront of Gapcheon is used as a park, which is a facility for leisure and recreation. In this problem, we model the Gapcheon as a slightly curved arc. In the arc, there are exactly 10^6 points marked by each centimeter. In Gapcheon, there are N bridges that connect two distinct points in the arc in a straight line segment. Such a line segment may touch other segments in an endpoint but never crosses them otherwise. For each pair of points, there exists at most one bridge that directly connects those two points. The city council is planning to place some lights in the bridges, to make Gapcheon as a more enjoyable place in the night. For each bridge, the city council calculated the aesthetical value if the lights are installed in these bridges. These value can be represented as a positive integer. However, too many lightings will annoy the residents at midnight. To address this issue, the council decided to make some regulations: for every arc between two adjacent points, there should be at most k lighted bridges visible from there. We call a line segment visible from an arc connecting i, i + 1, when one endpoint of the segment has an index at most i, and another endpoint of the segment has an index at least i + 1. The city council wants to consider the tradeoff between light pollution and the night view, so you should provide the maximum possible sum of aesthetical value, for all integers 1 ≤ k ≤ N. Input The first line contains an integer N. (1 ≤ N ≤ 250 000) The next N lines contain three integers Si, Ei, Vi, which denotes there is a straight line bridge connecting points Si, Ei, and having aesthetic value Vi. (1 ≤ Si < Ei ≤ 10^6, 1 ≤ Vi ≤ 10^9). It’s guaranteed that no lines connect the same pair of points, and no two different line segments cross. Output Print N integers separated by a space. The i-th integer (1 ≤ i ≤ N) should be the answer if k = i. Examples example input 1 6 1 2 10 2 3 10 1 3 21 3 4 10 4 5 10 3 5 19 example output 1 41 80 80 80 80 80 example input 2 4 1 5 1 2 5 1 3 5 1 4 5 1 example output 2 1 2 3 4
可以将题目转化一下,相当于用多个带有权值的线段来覆盖一个序列,使得每个元素被覆盖不超过$k$次
首先$k=1$是很好求的,用线段树搞一搞就行;但是并不能扩展到$k=i$
于是只能考虑同时处理所有$k=i$
一个简单、且好证的猜想:$k=2$相当于在$k=1$的基础上,将$k=1$用到的线段去掉后再跑一次$k=1$;也就是说两次之间是相互独立的
而且题面中有个十分重要的性质:所有的线段不相交,也就是说线段之间仅有包含/被包含关系
那么考虑将子线段合并为一个新的线段;这个 新的线段 和 包含子线段的最小线段 等价
合并的方法是,将区间内所有子线段弹出一个权值和最大的线段(有可能已经是合并过了的等价线段);如果一个子线段被弹空了那么就忽略它
但是这样一来带来了一个问题:如果$n$个线段是一个包含一个的(套娃),那么这棵划分树高度是$O(n)$的,则用堆处理复杂度是$O(n^2logn)$(需要将子线段全部插入到当前点)
但是用左偏树就很容易了,两个堆的合并用merge就完事;至于如何忽略被弹空的线段,我用的是set(反正这里的时间复杂度取决于merge的log)
(不知道为什么现场写的时候少了个$val[0]=-1$会出事...以后都加上就完事了)

#include <set> #include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; struct segment { int l,r,val; segment(int a=0,int b=0,int c=0) { l=a,r=b,val=c; } }; inline bool operator <(const segment &X,const segment &Y) { if(X.l!=Y.l) return X.l<Y.l; return X.r>Y.r; } typedef long long ll; const int N=1000005; int tot,ls[N],rs[N]; ll val[N]; int dis[N],fa[N]; //将根为x,y的两个堆合并 返回合并后的根 int merge(int x,int y) { if(!x || !y) return x+y; //此处为大根堆 if(val[x]<val[y]) swap(x,y); int &L=ls[x],&R=rs[x]; R=merge(R,y); fa[R]=x; if(dis[L]<dis[R]) swap(L,R); dis[x]=dis[R]+1; return x; } //将根为x的堆弹出堆顶 void pop(int x) { val[x]=-1; fa[ls[x]]=ls[x],fa[rs[x]]=rs[x]; fa[x]=merge(ls[x],rs[x]); } int find(int a) { if(fa[a]==a) return a; return fa[a]=find(fa[a]); } int n; segment a[N]; int cfa[N]; vector<int> v[N]; void dfs(int x) { set<int> s; for(int i=0;i<v[x].size();i++) { int y=v[x][i]; s.insert(y); dfs(y); } while(s.size()>1) { ll nsz=0; vector<int> clr; for(set<int>::iterator it=s.begin();it!=s.end();it++) { int cur=*it; int root=find(cur); nsz+=val[root]; pop(root); if(val[find(cur)]==-1) clr.push_back(cur); } ++tot; val[tot]=nsz,fa[tot]=tot; merge(find(x),tot); for(int i=0;i<clr.size();i++) s.erase(s.find(clr[i])); } if(!s.empty()) merge(find(x),find(*s.begin())); } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { int l,r,w; scanf("%d%d%d",&l,&r,&w); a[i]=segment(l,r,w); } a[n+1]=segment(0,1000001,-1); sort(a+1,a+n+2); cfa[1]=1; int dep=1; for(int i=2;i<=n+1;i++) { while(a[cfa[dep]].r<=a[i].l) dep--; v[cfa[dep]].push_back(i); cfa[++dep]=i; } tot=n+1; for(int i=1;i<=n+1;i++) fa[i]=i,val[i]=a[i].val; val[0]=-1; dfs(1); ll sum=0; for(int i=1;i<=n;i++) { int pos=find(1); if(val[pos]>0) { sum+=val[pos]; pop(pos); } printf("%lld",sum),putchar(i==n?'\n':' '); } return 0; }
(完)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号