决策单调性优化DP
可能需要莽一莽

大佬说是那就是,不狡辩
目录:
(之前的部分在论证理论正确性;如果功利一点、只想解决问题的话,直接从上一部分的最后开始看就行了)
假如对于某一个dp方程,$dp(i)$的最优转移是$dp(k)$,那么称$k$为$i$的决策点
而dp方程满足决策单调性指的是,决策点$k$随着$i$的增大保持单调不减(二维的情况稍微复杂一点,见下面的四边形不等式推决策单调性)
感觉有点类似斜率优化?
我们维护的下凸包,斜率也满足单调不减;所以如果斜率不等式的右侧是单调不减的(即决策时只需要向栈顶走、不需要在栈中二分),那么决策点也是单调不减的
所以绝大多数的斜率优化也满足决策单调性
一维状态dp的决策单调性比较直观,二维状态的就没那么显然了;需要借助其他的东西进行分析
而四边形不等式正是推出决策单调性的有力工具(虽然最后判断决策单调性都是打表)
四边形不等式一般满足这样的格式:
对于函数$f$和$\forall a,b,c,d$,且$a<b<c<d$,有
\[f(a,c)+f(b,d)\leq f(a,d)+f(b,c)\]
即 相交区间之和 $\leq$ 包含区间之和,那么函数$f$满足四边形不等式
拿一道具体的题目来说明吧
比如:Luogu P1880 (石子合并,$NOI1995$)
这道题目中,求最小得分满足决策单调性;最大得分却不满足(打表看出来的,没有证出来...)
计算最小得分,可以通过以下dp方程解决:记$dp(i,j)$表示将第$i\text{~}j$堆合并到一起的最小得分,$w(i,j)$表示第$i\text{~}j$堆的石子总数
则有$dp(i,j)=min\{dp(i,k)+dp(k+1,j)+w(i,j)\}$,其中$i<j$
一般来说,利用四边形不等式证明决策单调性的步骤大概是:
1. 证明$w(i,j)$满足四边形不等式
2. 证明$dp(i,j)$满足四边形不等式
3. 证明$dp(i,j)$满足决策单调性
1. 证明$w(i,j)$满足四边形不等式,即$w(i,j)+w(i+1,j+1)\leq w(i,j+1)+w(i+1,j)$
通过简单的求和即可证明,上述不等式恒取等号
2. 证明$dp(i,j)$满足四边形不等式,即$dp(i,j)+dp(i+1,j+1)\leq dp(i,j+1)+dp(i+1,j)$
这个我实在没证出来...听说可能可以用归纳法
3. 由$w(i,j),dp(i,j)$满足四边形不等式,推出$dp(i,j)$满足决策单调性
若记$dp(i,j)$由$s(i,j)=k$转移而来,$dp(i,j)$满足决策单调性就是指$s(i,j)$满足$s(i,j-1)\leq s(i,j)\leq s(i+1,j)$
先用反证法证明$s(i,j-1)\leq s(i,j)$
设$dp(i,j-1)$的最优转移为$x$,$dp(i,j)$的最优转移为$y$,且$y<x$,则有
\begin{align*}dp(i,j-1)&=dp_{k=x}(i,j-1)=dp(i,x)+dp(x+1,j-1)+w(i,j-1)\\ &\leq dp_{k=y}(i,j-1)=dp(i,y)+dp(y+1,j-1)+w(i,j-1)\end{align*}
\begin{align*}dp(i,j)&=dp_{k=y}(i,j)=dp(i,y)+dp(y+1,j)+w(i,j)\\ &\leq dp_{k=x}(i,j)=dp(i,x)+dp(x+1,j)+w(i,j)\end{align*}
由于$dp(i,j)$满足四边形不等式,于是有
\[dp(y+1,j-1)+dp(x+1,j)\leq dp(y+1,j)+dp(x+1,j-1)\]
对等式左右两边都加上$dp(i,x)+dp(i,y)+w(i,j-1)+w(i,j)$,得
\begin{align*}\text{左式}&=dp(i,y)+dp(y+1,j-1)+w(i,j-1)+dp(i,x)+dp(x+1,j)+w(i,j)\\ &=dp_{k=y}(i,j-1)+dp_{k=x}(i,j)\end{align*}
\begin{align*}\text{右式}&=dp(i,y)+dp(y+1,j)+w(i,j)+dp(i,x)+dp(x+1,j-1)+w(i,j-1)\\ &=dp_{k=y}(i,j)+dp_{k=x}(i,j-1)\end{align*}
于是有
\[dp_{k=y}(i,j-1)+dp_{k=x}(i,j)\leq dp_{k=y}(i,j)+dp_{k=x}(i,j-1)\]
在条件中,右式为$dp(i-1),dp(j)$的最优转移,应当比左式小,推出矛盾
于是,有$y\geq x$,即$s(i,j-1)\leq s(i,j)$
类似的,也可以用完全相同的方法反证得出$s(i,j)\leq s(i+1,j)$
(四边形不等式为$dp(i,y)+dp(i+1,x)\leq dp(i,x)+dp(i+1,y)$,左右两边都加上$dp(x+1,j)+dp(y+1,j)+w(i,j)+w(i+1,j)$)
由决策单调性,$s(i,j)$的大致情况就可以确定了
首先,$s(i,j)$是一个$n\times n$的上三角形
由于$s(i,j-1)\leq s(i,j)$,所以每一行从左到右都是单调不减的
又因为$s(i,j)\leq s(i+1,j)$,所以每一列从上到下也是单调不减的
然后考虑dp的顺序,由于$s(i,j-1)\leq s(i,j)\leq s(i+1,j)$,所以如果已知$s(i,j-1),s(i+1,j)$,那么$s(i,j)$的范围就会被限制住
所以dp的顺序应该是,外层$i$从大到小,内层$j$从小到大
这样一来可以计算整体的复杂度:
由于$s(i,j)$的范围被$s(i,j-1),s(i+1,j)$所限制,那么总的枚举次数就是$\sum_{i=1}^{n} \sum_{j=i}^{n} (s(i+1,j)-s(i,j-1))$,也就是时间复杂度
将括号内提出来,就是$\sum_{i=1}^{n} \sum_{j=i}^{n} s(i+1,j)-\sum_{i=1}^{n} \sum_{j=i}^{n} s(i,j-1)$,其中
\[\sum_{i=1}^{n}\sum_{j=1}^{n}s(i+1,j)\leq \sum_{i=2}^{n}\sum_{j=i}^{n}s(i,j)+2n^2\]
\[\sum_{i=1}^{n}\sum_{j=1}^{n}s(i,j-1)\geq \sum_{i=1}^{n-1}\sum_{j=i}^{n-1}s(i,j)\]
于是就能得到
\begin{align*}&\sum_{i=1}^{n} \sum_{j=i}^{n} s(i+1,j)-\sum_{i=1}^{n} \sum_{j=i}^{n} s(i,j-1)\\ \leq &\sum_{i=2}^{n}\sum_{j=i}^{n}s(i,j)+2n^2-\sum_{i=1}^{n-1}\sum_{j=i}^{n-1}s(i,j)\\ \leq &\sum_{i=1}^{n} s(i,n)+2n^2\\ \leq &\ 3n^2\end{align*}
所以这种方法的时间复杂度为$O(n^2)$
这里就不写环状的了,反正只是把$a_i$再复制一份而已

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=1005; const int INF=1<<30; int n; int a[N],pre[N]; int s[N][N]; int dp[N][N]; int main() { // freopen("input.txt","r",stdin); // freopen("my.txt","w",stdout); scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]),pre[i]=pre[i-1]+a[i]; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) dp[i][j]=INF; for(int i=1;i<=n;i++) s[i][i]=i,dp[i][i]=0; for(int i=n-1;i>=1;i--) for(int j=i+1;j<=n;j++) for(int k=s[i][j-1];k<=s[i+1][j];k++) { int val=dp[i][k]+dp[k+1][j]+pre[j]-pre[i-1]; if(val<dp[i][j]) { s[i][j]=k; dp[i][j]=val; } } printf("%d\n",dp[1][n]); return 0; }
附上数据生成器(虽然十分简单...)

#include <ctime> #include <cstdio> #include <cstdlib> #include <cstring> #include <algorithm> using namespace std; int rnd(int lim) { return (rand()*rand()+rand()-1)%lim+1; } int main() { freopen("input.txt","w",stdout); srand(time(NULL)); int n=205; printf("%d\n",n); for(int i=1;i<=n;i++) printf("%d ",rnd(1000)); return 0; }
解决(其实只是初步了解)了四边形不等式之后,就来处理一下更常见的一维决策单调性问题吧
继续拉来斜率优化的例题:HDU 3507 ($Print\ Article$)
令$S(i)=\sum_{i=1}^{i} C_i$,则dp方程为$dp(i)=min\{dp(j)+(S(i)-S(j))^2\}+M$
我们可以令$w(j,i)=(S(i)-S(j))^2$,那么可以证明$w(j,i)$满足四边形不等式
若令$a<b<c<d$,则有
\begin{align*}w(a,c)+w(b,d)=&((S(c)-S(a))^2+((S(d)-S(b))^2\\ =&S(a)^2+S(b)^2+S(c)^2+S(d)^2-2S(a)S(c)-2S(b)S(d)\end{align*}
\begin{align*}w(a,d)+w(b,c)=&((S(d)-S(a))^2+((S(c)-S(b))^2\\ =&S(a)^2+S(b)^2+S(c)^2+S(d)^2-2S(a)S(d)-2S(b)S(c)\end{align*}
由排序不等式的乱序和大于逆序和,有
\[S(a)S(c)+S(b)S(d)+S(c)S(a)+S(d)S(b)\geq S(a)S(d)+S(b)S(c)+S(c)S(b)+S(d)S(a)\]
所以$w(a,c)+w(b,d)\leq w(a,d)+w(b,c)$
再用类似石子合并的反证法证明决策单调性:
令$dp(i)$的最优转移为$x$,$dp(i+1)$的最优转移为$y$,且$y<x$,则有
\begin{align*}dp(i)&=dp_{j=x}(i)=dp(x)+w(x,i)+M\\ &\leq dp_{j=y}(i)=dp(y)+w(y,i)+M\end{align*}
\begin{align*}dp(i+1)&=dp_{j=y}(i+1)=dp(y)+w(x,i+1)+M\\ &\leq dp_{j=x}(i+1)=dp(x)+w(x,i+1)+M\end{align*}
于是构造四边形不等式$w(y,i)+w(x,i+1)\leq w(y,i+1)+w(x,i)$,并在左右两边都加上$dp(x)+dp(j)+2M$,那么
\begin{align*}\text{左式}&=dp(x)+w(x,i+1)+M+dp(y)+w(y,i)+M\\ &=dp_{j=x}(i+1)+dp_{j=y}(i)\end{align*}
\begin{align*}\text{右式}&=dp(x)+w(x,i)+M+dp(y)+w(y,i+1)+M\\ &=dp_{j=x}(i)+dp_{j=y}(i+1)\end{align*}
根据条件,右式为$dp(i),dp(j)$的最优转移,应当比左式小,于是推出矛盾
所以$dp(i)$满足决策单调性
这样看来,只要证明转移的差值$w(i,j)$满足四边形不等式,就能证出一维dp的决策单调性;这个还是比较方便的
虽然上面的内容能够证明某个dp方程是否满足决策单调性,但是离具体的实现还有点差距
学习了这篇的实现方法,讲的很好:ReMoon - 关于决策单调性优化动态规划
根据dalao的文章,一共有两种可能的情况:1. 被决策点不会成为决策点;2. 被决策点可能会成为决策点
1. 被决策点不会成为决策点
一般的遇到这种情况时,dp方程有两维
比如,$dp(i,j)$表示在第$i$个阶段、对$j$做决策;$dp(i,j)$由$dp(i-1,k)$转移得来
这种情况下,$dp(i,j)$不会成为$dp(i,j')$的决策点(因为必须从第$i-1$阶段转移),所以可以比较简单地处理
//l,r: 被决策点的下/上界 //L,R: 决策点的下/上界 void Solve(int i,int l,int r,int L,int R) { if(l>r) return; // mid: [l,r]中二分被决策点 // pos: mid的决策点 int pos=-1,mid=(l+r)>>1; for(int j=L;j<=min(mid-1,R);j++) { int val=dp[i-1][j]+w(j,mid); if(val<dp[i][mid]) dp[i][mid]=val,pos=j; } Solve(i,l,mid-1,L,pos); Solve(i,mid+1,r,pos,R); }
分析一下时间复杂度
我们在每层递归中,都将当前区间$[l,r]$分成长度相等的两部分$[l,mid-1],[mid+1,r]$,这两部分的被决策点范围为$[L,pos],[pos,R]$
那么在下一层递归中,枚举被决策点的次数就是$(R-pos+1)+(pos-L+1)=R-L+2$
于是在每一层中枚举的次数是$n$级别的,一共递归$logn$层,所以总的复杂度为$O(n\cdot logn)$
例题:牛客ACM 890J ($Wood\ Processing$,$2019$牛客暑期多校第十场)
把所有木板按高度排序后,记$dp(i,j)$表示,第$i$次切木板、切到第$j$块时,浪费的最小面积;$w(i,j)$表示从第$i$到第$j$为一块所要浪费的面积
那么$dp(i,j)=min\{dp(i-1,k)+w(k+1,j)\},w(i,j)=\sum_{k=i}^{j}(W_k\cdot H_k)-H_i\cdot \sum_{k=i}^{j}W_k$
很容易证得$w(i,j)$满足四边形不等式($\sum (W_k\cdot H_k)$能消去,之后就很显然了),于是也满足决策单调性,套用上面的递归即可

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef pair<int,int> pii; typedef long long ll; const int N=5005; const int K=2005; const ll INF=1LL<<60; int n,k; pii a[N]; ll sum[N],W[N]; ll dp[K][N]; inline ll w(int i,int j) { return sum[j]-sum[i-1]-ll(a[i].first)*(W[j]-W[i-1]); } void Solve(int i,int l,int r,int L,int R) { if(l>r) return; int pos=-1,mid=(l+r)>>1; for(int j=L;j<=min(mid-1,R);j++) { ll val=dp[i-1][j]+w(j+1,mid); if(val<dp[i][mid]) dp[i][mid]=val,pos=j; } Solve(i,l,mid-1,L,pos); Solve(i,mid+1,r,pos,R); } int main() { scanf("%d%d",&n,&k); for(int i=1;i<=n;i++) scanf("%d%d",&a[i].second,&a[i].first); sort(a+1,a+n+1); for(int i=1;i<=n;i++) { sum[i]=sum[i-1]+ll(a[i].first)*a[i].second; W[i]=W[i-1]+a[i].second; } for(int i=0;i<=k;i++) for(int j=0;j<=n;j++) dp[i][j]=INF; dp[0][0]=0; for(int i=1;i<=k;i++) Solve(i,1,n,0,n-1); printf("%lld\n",dp[k][n]); return 0; }
2. 被决策点可能会成为决策点
也有不少dp方程属于这种情况,比如上面举的$Print\ Article$
由于被决策点会成为后续点的决策点,于是在计算$dp(i)$时,它的决策点$j$的值$dp(j)$是未被计算的,所以并不能采用上面的整体二分
因为决策点必然是需要被提前计算的,所以从左向右dp,不过在这个过程中多维护一些信息
我们考虑对于每个被决策点,其决策点的变化过程
(1). 在初始情况下,每个点都由$0$转移来,于是决策点数列为$0,0,0,...,0$
(2). 假设对于被决策点$i$,由$1$转移比由$0$转移来的更优
那么根据决策单调性,$i+1,i+2,i+3,...$的决策点也不小于$1$,于是对于它们来说从$1$转移也比从$0$更优
此时决策点数列为$0,0,...,0,1,1,...,1$,可以发现$1$的出现位置满足单调性,所以可以二分得出$1$的最早出现位置
(3). 类似的,对于从$2$转移的情况,也是覆盖了一段$[j,n]$的决策点区间,其中$j$可以二分得到($j$有可能小于$1$的最早出现位置$i$,即$2$彻底覆盖$1$)
以此类推
于是考虑维护一个栈来保存决策点$x$的最早出现位置
//cur: 当前栈指针 top: 栈顶指针 int cur,top; //pos: 决策点对应的最小被决策点 from: 决策点 int pos[N],from[N]; ll dp[N]; //找到以i作为决策点的最小被决策点(与栈顶的决策点相比即可) inline int Find(int i) { int l=i+1,r=n+1,mid;//l=pos[top]也可以,因为在Solve()中已经弹出过会被覆盖的决策点了 while(l<r) { mid=(l+r)>>1; if(dp[from[top]]+w(from[top],mid)>dp[i]+w(i,mid)) r=mid; else l=mid+1; } return l; } void Solve() { cur=top=0; for(int i=1;i<=n;i++) { if(cur<top && pos[cur+1]==i) cur++; dp[i]=dp[from[cur]]+w(from[cur],i); // 当i的决策区间能完全覆盖栈顶决策点的决策区间 while(top>cur && dp[from[top]]+w(from[top],pos[top])>dp[i]+w(i,pos[top])) top--; int to=Find(i); if(to<=n) ++top,pos[top]=to,from[top]=i; } }
这道题接下来就没什么了

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=500005; int n,M; ll a[N],sum[N]; inline ll w(int i,int j) { return (sum[j]-sum[i])*(sum[j]-sum[i])+M; } int cur,top; int pos[N],from[N]; ll dp[N]; inline int Find(int i) { int l=i+1,r=n+1,mid; while(l<r) { mid=(l+r)>>1; if(dp[from[top]]+w(from[top],mid)>dp[i]+w(i,mid)) r=mid; else l=mid+1; } return l; } void Solve() { cur=top=0; for(int i=1;i<=n;i++) { if(cur<top && pos[cur+1]==i) cur++; dp[i]=dp[from[cur]]+w(from[cur],i); while(top>cur && dp[from[top]]+w(from[top],pos[top])>dp[i]+w(i,pos[top])) top--; int to=Find(i); if(to<=n) ++top,pos[top]=to,from[top]=i; } } int main() { while(~scanf("%d%d",&n,&M)) { for(int i=1;i<=n;i++) scanf("%lld",&a[i]),sum[i]=sum[i-1]+a[i]; Solve(); printf("%lld\n",dp[n]); } return 0; }
CF 868F ($Yet\ Another\ Minimization\ Problem$)
很明显属于被决策点不会成为决策点的情况,但是比较tricky的是$w(i,j)$没有办法预处理
可以采用two pointers用类似莫队的方法计算$w(i,j)$
由于每一次查询$w(i,j)$时,$i,j$最多移动$R-L+1$次,所以总的复杂度也是$O(n\cdot logn)$

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const ll INF=1LL<<60; const int N=100005; const int K=22; int n,k; int a[N]; ll dp[K][N]; int cnt[N]; ll res; int wl=1,wr=0; inline ll w(int i,int j) { while(wl<i) { cnt[a[wl]]--; res-=cnt[a[wl]]; wl++; } while(wl>i) { wl--; res+=cnt[a[wl]]; cnt[a[wl]]++; } while(wr<j) { wr++; res+=cnt[a[wr]]; cnt[a[wr]]++; } while(wr>j) { cnt[a[wr]]--; res-=cnt[a[wr]]; wr--; } return res; } void Solve(int i,int l,int r,int L,int R) { if(l>r) return; int pos=-1,mid=(l+r)>>1; for(int j=L;j<=min(mid-1,R);j++) if(dp[i][mid]>dp[i-1][j]+w(j+1,mid)) { dp[i][mid]=dp[i-1][j]+w(j+1,mid); pos=j; } Solve(i,l,mid-1,L,pos); Solve(i,mid+1,r,pos,R); } int main() { scanf("%d%d",&n,&k); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=0;i<=k;i++) for(int j=0;j<=n;j++) dp[i][j]=INF; dp[0][0]=0; for(int i=1;i<=k;i++) Solve(i,1,n,0,n-1); printf("%lld\n",dp[k][n]); return 0; }
BZOJ 5125 (小$Q$的书架)
首先证明一下转移权值$w(i,j)$满足四边形不等式:
由于区间排序 交换相邻元素次数 等于 逆序对个数,所以$w(i,j)=\text{区间}[i,j]\text{中逆序对个数}$
令$a<b<c<d$,即证明$w(a,c)+w(b,d)\leq w(a,d)+w(b,c)$
对于区间来说,$[a,c]=[a,b)+[b,c],[b,d]=[b,c]+(c,d],[a,d]=[a,b)+[b,c]+(c,d]$;由于区间$[a,d]$中,$[a,b),(c,d]$间还会贡献逆序对数,所以上面的四边形不等式显然成立
然后考虑如何计算$w(i,j)$:
由于无法预处理,所以可以采用上题一样的two pointers
但是加入/删除一个元素时逆序对的变化肯定是无法$O(1)$做到的,于是可以考虑用树状数组维护每个编号是否出现
若将左指针$wl$左移,逆序对数就加上$[wl,wr]$中$a_i<a_{wl}$的个数;若将右指针$wr$右移,逆序对数就加上$[wl,wr]$中$a_i>a_{wr}$的个数;删除类似
于是可以$O(n\cdot log^2n)$解决

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const ll INF=1LL<<60; const int N=40005; const int K=11; int n,k; int a[N]; int t[N<<1]; inline void Modify(int k,int x) { for(int i=k;i<=n;i+=(i&(-i))) t[i]+=x; } inline int Query(int k) { int res=0; for(int i=k;i;i-=(i&(-i))) res+=t[i]; return res; } int wl,wr; ll res; inline ll w(int i,int j) { while(wl<i) { res-=Query(a[wl]-1); Modify(a[wl],-1); wl++; } while(wl>i) { wl--; res+=Query(a[wl]-1); Modify(a[wl],1); } while(wr<j) { wr++; res+=Query(n)-Query(a[wr]); Modify(a[wr],1); } while(wr>j) { res-=Query(n)-Query(a[wr]); Modify(a[wr],-1); wr--; } return res; } ll dp[K][N]; void Solve(int i,int l,int r,int L,int R) { if(l>r) return; int pos=-1,mid=(l+r)>>1; dp[i][mid]=INF; for(int j=L;j<=min(mid-1,R);j++) if(dp[i][mid]>dp[i-1][j]+w(j+1,mid)) { dp[i][mid]=dp[i-1][j]+w(j+1,mid); pos=j; } Solve(i,l,mid-1,L,pos); Solve(i,mid+1,r,pos,R); } void Clear() { wl=1,wr=0; res=0; for(int i=1;i<=n;i++) t[i]=0; } int main() { scanf("%d%d",&n,&k); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<=n;i++) dp[0][i]=INF; for(int i=1;i<=k;i++) { Clear(); Solve(i,1,n,0,n-1); } printf("%lld\n",dp[k][n]); return 0; }
暂时就先这样吧,以后有题慢慢补充
Codeforces Gym 102920L (Two Buildings)
如果令$h'[i]=-h[i]$,那么可以改写条件为“使得$(h[i]-h'[j])\cdot (j-i)$最大”,即使得一个底为$j-i$、高为$h[i]-h'[j]$的长方形面积最大。
现在考虑,哪些情况下$h$和$h'$中的元素一定不会出现在较优解中。
如果$j>i$,且有$h[j]\leq h[i]$,那么选择$h[j]$一定不如$h[i]$,因为底和高同时变小;类似的,如果$j>i$,且有$h'[j]\leq h'[i]$,则选择$h'[i]$一定不如选择$h'[j]$。
那么最后两个点集一定呈现形如这样的趋势:
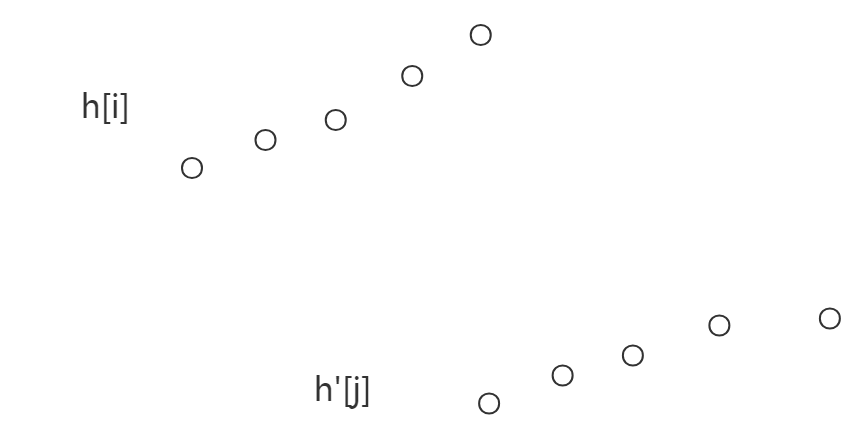
现在考虑是否满足决策单调性:假设有两个被决策点$i_1,i_2$($i_1<i_2$)和两个决策点$j_1,j_2$($j_1<j_2$),其中$j_2$是$i_1$的最优转移,我们需要检验$j_1$是否可能是$i_2$的最优转移。
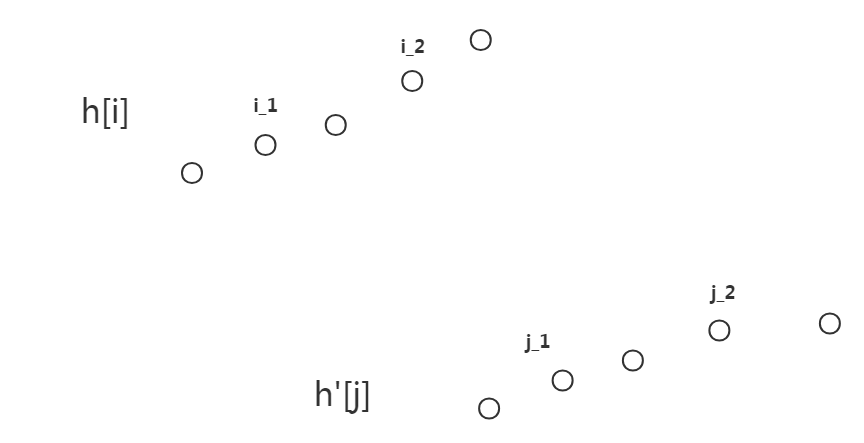
由$j_2$是$i_1$的最优转移,若从两长方形面积之差来考虑即有
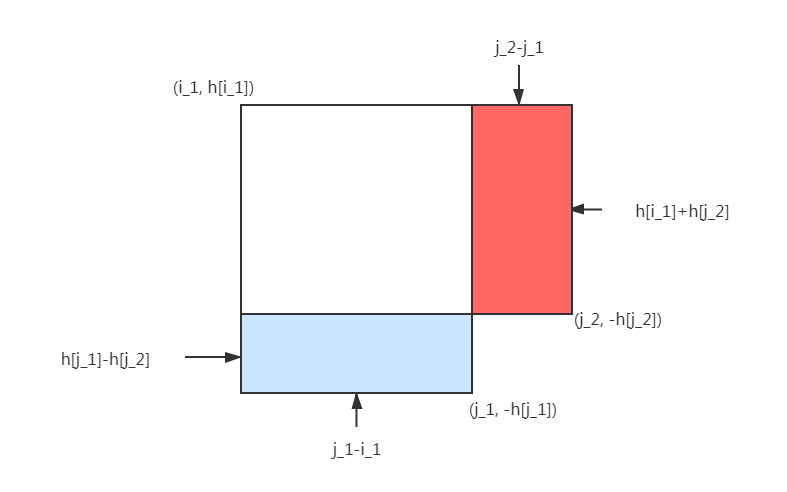
\[(h[i_1]+h[j_2])(j_2-j_1)>(h[j_1]-h[j_2])(j_1-i_1)\]
那么考虑若$j_1$为$i_2$的最优转移,从长方形面积之差考虑则应该有
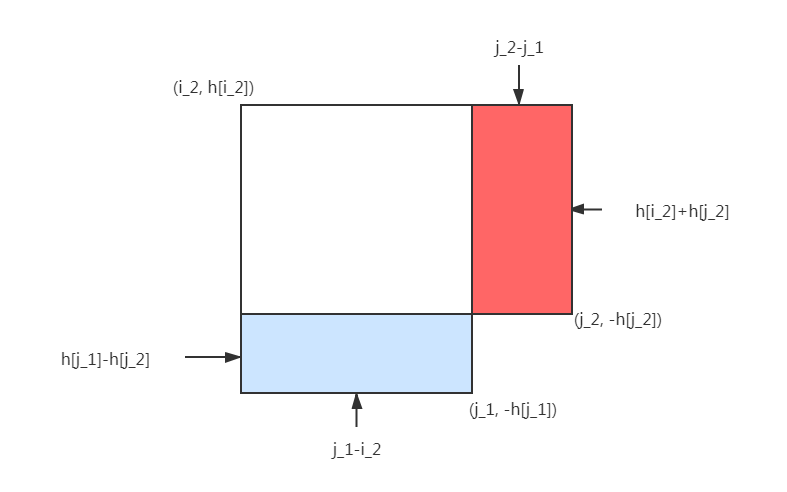
\[(h[j_1]-h[j_2])(j_1-i_2)>(h[i_2]+h[j_2])(j_2-j_1)\]
不过根据$i_1,i_2,j_1,j_2$间的关系,我们显然能得到$h[i_2]+h[j_2]>h[i_1]+h[j_2]$、$j_1-i_1>j_1-i_2$,进行联立即可得到
\[(h[i_2]+h[j_2])(j_2-j_1)>(h[i_1]+h[j_2])(j_2-j_1)>(h[j_1]-h[j_2])(j_1-i_1)>(h[j_1]-h[j_2])(j_1-i_2)\]
那么显然$(h[j_1]-h[j_2])(j_1-i_2)>(h[i_2]+h[j_2])(j_2-j_1)$永远不会成立,从而得到具有决策单调性。注意:若不删去$h,h'$中的非较优点,上式不一定成立。

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef pair<int,int> pii; const int N=1000005; inline void read(int &x) { char ch=getchar();int sum=0; while(!(ch>='0'&&ch<='9') && !(ch=='-'))ch=getchar(); if(ch=='-')x=-1,ch=getchar();else x=1; while(ch>='0'&&ch<='9')sum=sum*10+ch-48,ch=getchar(); x*=sum; } int n; int h[N]; vector<pii> vu,vd; ll ans=0; inline void solve(int l,int r,int L,int R) { if(l>r) return; ll tmp=0; int mid=(l+r)>>1,pos=L; for(int i=L;i<=R;i++) { ll val=1LL*(vd[i].first+vu[mid].first)*(vd[i].second-vu[mid].second); if(val>tmp) tmp=val,pos=i; } ans=max(ans,tmp); solve(l,mid-1,L,pos); solve(mid+1,r,pos,R); } int main() { read(n); for(int i=1;i<=n;i++) read(h[i]); for(int i=1;i<=n;i++) { if(vu.empty() || h[i]>vu.back().first) vu.emplace_back(pii(h[i],i)); while(!vd.empty() && h[i]>=vd.back().first) vd.pop_back(); vd.emplace_back(pii(h[i],i)); } solve(0,vu.size()-1,0,vd.size()-1); printf("%lld\n",ans); return 0; }
(完)



