笛卡尔树
听上去有丶厉害,实际也很巧妙
学习了这两篇:ReMoon - 单调栈的应用 --- 笛卡尔树与虚树
ACM算法日常 - 算法合集 | 神奇的笛卡尔树 - HDU 1506
板子:

struct Cartesian { int root; int ls[N],rs[N]; vector<int> v; void clear() { root=0; v.clear(); for(int i=1;i<n;i++) ls[i]=rs[i]=0; } void build(int *a) { for(int i=1;i<n;i++) { int j=0; //a[v.back()]<a[i] 大根 //a[v.back()]>a[i] 小根 while(v.size() && a[v.back()]<a[i]) j=v.back(),v.pop_back(); if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } };
~ 简介 ~
虽然名字中带有“树”,但是笛卡尔树其实是对于一个序列的转化,并通过这个转化获得更多此序列的信息
对于一个简单的序列:$2,8,5,7,1,4$,我们可以建立如下的小根笛卡尔树($pos$表示原序列中的位置,$val$表示该位置的值)
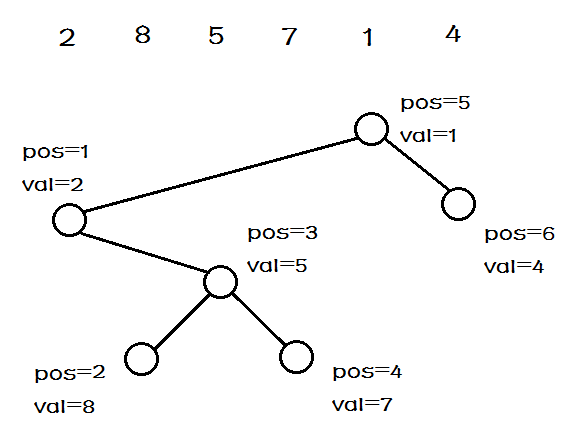
笛卡尔树有这样的基本性质:
对于树上的任意一点$x$和左右儿子$left,right$,有:
1. $pos[left]<pos[x]<pos[right]$(维持原序列的顺序)
2. $val[x]<val[left],val[right]$(大根此时则恰恰相反)
即一般讲解所说的$pos$满足二叉查找树,$val$满足堆
直观点说,就是这两条延伸性质:
以树上任意一点$x$为根构成的子树中,
1. 各节点的$pos$是连续的,且对$pos$的中序遍历即为原序列顺序(由$pos$满足二叉查找树可得)
2. $x$点的$val$为全子树最小(由$val$满足堆可得)
~ 建树 ~
有了对笛卡尔树结构的了解,现在考虑怎么建立这棵树
【方法一】优先满足$val$(别真这样写啊...只是提一嘴)
要想优先满足$val$的条件,那就必须从顶向下建树了
利用上面的延伸性质2,每次选取当前区间$[l,r]$中$val$的最小值所在的$pos$(记$pos=i$)作为子树的根节点
然后对于$[l,i-1],[i+1,r]$递归地不断重复上述过程
其中选取区间$val$最小值所在的$pos$可以使用线段树优化
总复杂度$O(nlogn)$

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=100005; const int INF=1<<30; int n; int val[N]; int sz; int t[N<<2]; inline void Add(int i) { int k=i+sz-1; t[k]=i; k>>=1; while(k) { int left=t[k<<1],right=t[k<<1|1]; t[k]=(val[left]<val[right]?left:right); k>>=1; } } inline int Query(int k,int l,int r,int a,int b) { if(a>r || b<l) return 0; if(a>=l && b<=r) return t[k]; int mid=(a+b)>>1; int left=Query(k<<1,l,r,a,mid),right=Query(k<<1|1,l,r,mid+1,b); return (val[left]<val[right]?left:right); } void Init() { sz=1; while(sz<n) sz<<=1; val[0]=INF; for(int i=1;i<(sz<<1);i++) t[i]=0; for(int i=1;i<=n;i++) Add(i); } int ls[N],rs[N]; inline int Build(int l,int r) { if(l>r) return 0; int pos=Query(1,l,r,1,sz); ls[pos]=Build(l,pos-1); rs[pos]=Build(pos+1,r); return pos; } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&val[i]); Init(); int root=Build(1,n); /* for(int i=1;i<=n;i++) printf("i=%d: ls=%d rs=%d\n",i,ls[i],rs[i]);*/ return 0; }
【方法二】优先满足$pos$
由于对于子树的先序遍历是原序列顺序,所以考虑按$i=1\text{ ~ }n$的顺序依次加入节点并调整树的结构,使得当前的树为子序列$[1,i]$所构成的笛卡尔树
由于$pos$满足二叉排序树,而$i$在区间$[1,i]$中$pos$最大,所以$i$插入的位置为 序列$[1,i-1]$所构成的笛卡尔树的根节点 一直向右儿子走、直到走到了空节点
这样插入后,$i$的$pos$已经满足要求了,但是$val$却不一定满足堆
于是考虑怎么调整当前的树
若$i$的$val$不满足要求,即存在某(些)祖先$j$,使得$j$为根的子树中$val$全大于$val[i]$;显然我们需要通过调整$i$的位置,使得$i$成为$j$的祖先
是这样操作的:
0. 刚刚插入完成后,可能树是这样的
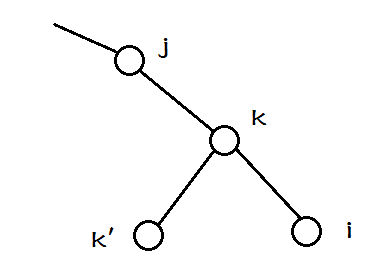
1. 将$i$向上一层移动;这时由于$pos[k]<pos[i]$,所以$k$成为$i$的左儿子,$k'$依然是$k$的左儿子

2. 继续将$i$向上一层移动,相似的,$j$也应当属于$i$的左子树;不妨让$j$为$i$的左儿子,$k$为$j$的右儿子(此时有多种调整方法;但当我们使用这种调整方法时,$j,k,k'$相互间与原来的连边相同)

以上的调整操作都是在$[1,i-1]$序列构成的笛卡尔树的最右链(即从根节点一直向右儿子走的这条路径)上进行的
在处理完后,我们对比一下调整前后的树结构,发现只有很少的地方出现了变化:
1. $k$的右儿子变成了空节点
2. $j$的父亲变成了$i$,且$j$是$i$的左儿子
3. $i$继承了原来$j$的父亲
事实上,即使$i$到$j$的路径很长很长,一共也只有这三个地方发生了变化,所以我们的调整不是很复杂
现在最大的问题变成,如何找到$j$
目光回到最右链上,由于$val$满足堆,于是最右链上的各节点$val$是单调递增的;可以考虑用单调栈维护,栈中装的是最右链上节点的$pos$
而我们要找的$j$,就是$val[j]<val[i]$、且最靠近栈底的元素
原理理解了之后,重新整理一下思路,尽量简单清楚地建笛卡尔树:
1. 用单调栈维护最右链
2. 每次插入当前的$i$,在单调栈中不停弹出栈顶,直到栈顶$fa$满足$val[fa]<val[i]$,则最后一次弹出的就是$j$
3. 将$i$作为$fa$的右儿子,$j$作为$i$的左儿子
是不是很简单owo
复杂度$O(n)$,是相当优秀的一种方法

#include <cstdio> #include <cstring> #include <algorithm> #include <vector> using namespace std; const int N=100005; int n; int a[N]; int root; int ls[N],rs[N]; vector<int> v; void Build() { for(int i=1;i<=n;i++) { int j=0; while(v.size() && a[v.back()]>a[i]) { j=v.back(); v.pop_back(); } if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); Build(); /* for(int i=1;i<=n;i++) printf("i=%d ls=%d rs=%d\n",i,ls[i],rs[i]);*/ return 0; }
所以在一些情况下,笛卡尔树的题目可以不用建树,直接用单调栈就够了
~应用~
最简单的一个应用是求元素的左右延伸区间
具体点说,就是对于一个数列$a$,询问以$a[i]$为区间最大(小)值的最长区间
使用笛卡尔树,就可以通过$O(n)$的预处理做到$O(1)$查询:进行中序遍历,每个节点$x$的子树的$pos$最小、最大值就是答案
模板题:HDU 1506 (Largest Rectangle in a Histogram)

#include <cstdio> #include <cstring> #include <algorithm> #include <vector> using namespace std; typedef long long ll; const int N=100005; int n; int a[N]; int root; int ls[N],rs[N]; vector<int> v; void Build() { v.clear(); memset(ls,0,sizeof(ls)); memset(rs,0,sizeof(rs)); for(int i=1;i<=n;i++) { int j=0; while(v.size() && a[v.back()]>a[i]) { j=v.back(); v.pop_back(); } if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } int l[N],r[N]; void dfs(int x) { l[x]=r[x]=x; if(ls[x]) { dfs(ls[x]); l[x]=l[ls[x]]; } if(rs[x]) { dfs(rs[x]); r[x]=r[rs[x]]; } } int main() { scanf("%d",&n); while(n) { for(int i=1;i<=n;i++) scanf("%d",&a[i]); Build(); dfs(root); ll ans=0; for(int i=1;i<=n;i++) ans=max(ans,ll(a[i])*(r[i]-l[i]+1)); printf("%lld\n",ans); scanf("%d",&n); } return 0; }
一个稍微高级一点的应用,就是给出分治的边界
一道不错的题:Luogu P4755 (Beautiful Pair)
官方题解已经很完善了:FlierKing - 题解 P4755 【Beautiful Pair】
简单点说,就是每次取当前区间$[l,r]$的最大值$a_i$,那么$i$即为笛卡尔树中 此区间对应子树的根节点
于是将区间分成两部分$[l,i-1],[i+1,r]$的操作,就可以转化成笛卡尔树上的分治
同时,这个题解将“统计$[l,r]$中$a_i\leq x$的数量”这个主席树问题,离线后通过拆分转化为树状数组问题,设计十分巧妙

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef pair<int,int> pii; const int N=100005; int n; int a[N]; int root; int ls[N],rs[N]; vector<int> v; void Build() { for(int i=1;i<=n;i++) { int j=0; while(v.size() && a[v.back()]<a[i]) { j=v.back(); v.pop_back(); } if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } int l[N],r[N]; inline void dfs(int x) { if(ls[x]) { dfs(ls[x]); l[x]=l[ls[x]]; } else l[x]=x; if(rs[x]) { dfs(rs[x]); r[x]=r[rs[x]]; } else r[x]=x; } vector<pii> add[N]; inline void Solve(int x) { int lp=x-l[x],rp=r[x]-x; if(lp<rp) for(int i=l[x];i<=x;i++) { add[r[x]].push_back(pii(a[x]/a[i],1)); add[x-1].push_back(pii(a[x]/a[i],-1)); } else for(int i=x;i<=r[x];i++) { add[x].push_back(pii(a[x]/a[i],1)); add[l[x]-1].push_back(pii(a[x]/a[i],-1)); } if(ls[x]) Solve(ls[x]); if(rs[x]) Solve(rs[x]); } vector<int> pos; int t[N]; inline int lowbit(int x) { return x&(-x); } inline void Add(int k,int x) { for(int i=k;i<=n;i+=lowbit(i)) t[i]+=x; } inline int Query(int k) { int res=0; for(int i=k;i;i-=lowbit(i)) res+=t[i]; return res; } int main() { scanf("%d",&n); pos.push_back(0); for(int i=1;i<=n;i++) scanf("%d",&a[i]),pos.push_back(a[i]); sort(pos.begin(),pos.end()); pos.resize(unique(pos.begin(),pos.end())-pos.begin()); Build(); dfs(root); Solve(root); ll ans=0; for(int i=1;i<=n;i++) { int p=lower_bound(pos.begin(),pos.end(),a[i])-pos.begin(); Add(p,1); for(int j=0;j<add[i].size();j++) { int lim=lower_bound(pos.begin(),pos.end(),add[i][j].first)-pos.begin(); if(pos[lim]>add[i][j].first) lim--; ans=ans+add[i][j].second*Query(lim); } } printf("%lld\n",ans); return 0; }
学完之后立马就现场碰到基本一样的题...
牛客ACM 883G (Removing Stones,2019牛客暑期多校训练营(第三场))
只不过对于当前区间,是遍历较小的那一半、并在另一半二分

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=300005; int n; int a[N]; ll p[N]; int root; int ls[N],rs[N]; vector<int> v; void Build() { for(int i=1;i<=n;i++) { int j=0; while(v.size() && a[v.back()]<a[i]) { j=v.back(); v.pop_back(); } if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } int l[N],r[N]; inline void dfs(int x) { if(ls[x]) { dfs(ls[x]); l[x]=l[ls[x]]; } else l[x]=x; if(rs[x]) { dfs(rs[x]); r[x]=r[rs[x]]; } else r[x]=x; } ll ans=0; void Solve(int x) { ll sum=0; int lp=x-l[x]+1,rp=r[x]-x+1; int left,right,mid; if(lp<rp) for(int i=x;i>=l[x];i--) { sum+=a[i]; left=x,right=r[x]+1,mid; while(left<right) { mid=(left+right)>>1; if(sum+p[mid]-p[x]<2LL*a[x]) left=mid+1; else right=mid; } ans+=r[x]-left+1; } else for(int i=x;i<=r[x];i++) { sum+=a[i]; left=l[x],right=x,mid; while(left<right) { mid=(left+right)>>1; if(sum+p[x-1]-p[mid-1]>=2LL*a[x]) left=mid+1; else right=mid; } if(sum+p[x-1]-p[left-1]<2LL*a[x]) left--; ans+=left-l[x]+1; } if(ls[x]) Solve(ls[x]); if(rs[x]) Solve(rs[x]); } void Clear() { ans=0; v.clear(); for(int i=1;i<=n;i++) ls[i]=rs[i]=0; } int main() { int T; scanf("%d",&T); while(T--) { Clear(); scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]),p[i]=p[i-1]+a[i]; Build(); dfs(root); Solve(root); printf("%lld\n",ans); } return 0; }
一道比较明显的题:HDU 6701 (Make Rounddog Happy,2019 Multi-University Training Contest 10)
由于需要对$a_l,...,a_r$求max,所以能比较自然地想到笛卡尔树上分治
然后就是处理区间内数字不同的限制;不过也并不困难,只要正向、反向各扫一遍就能预处理出来$i$向左、向右不出现重复数字的最大延伸长度了

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=300005; int n,k; int a[N]; int root; int ls[N],rs[N]; vector<int> v; void Build() { v.clear(); for(int i=1;i<=n;i++) { int j=0; while(v.size() && a[v.back()]<a[i]) { j=v.back(); v.pop_back(); } if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } int l[N],r[N]; void dfs(int x) { l[x]=r[x]=x; if(ls[x]) dfs(ls[x]),l[x]=l[ls[x]]; if(rs[x]) dfs(rs[x]),r[x]=r[rs[x]]; } int cnt[N]; int L[N],R[N]; ll ans=0; void Solve(int x) { int lp=x-l[x],rp=r[x]-x; if(lp<rp) { for(int i=l[x];i<=x;i++) ans+=max(0,min(R[i],r[x])-max(a[x]-k+i-1,x)+1); } else { for(int i=x;i<=r[x];i++) ans+=max(0,min(k-a[x]+i+1,x)-max(L[i],l[x])+1); } if(ls[x]) Solve(ls[x]); if(rs[x]) Solve(rs[x]); } int main() { int T; scanf("%d",&T); while(T--) { scanf("%d%d",&n,&k); ans=0; for(int i=1;i<=n;i++) ls[i]=rs[i]=0; for(int i=1;i<=n;i++) scanf("%d",&a[i]); Build(); dfs(root); int j=1; for(int i=1;i<=n;i++) { cnt[a[i]]++; while(cnt[a[i]]>1) { R[j]=i-1; cnt[a[j]]--; j++; } } for(int i=j;i<=n;i++) R[i]=n,cnt[a[i]]--; j=n; for(int i=n;i>=1;i--) { cnt[a[i]]++; while(cnt[a[i]]>1) { L[j]=i+1; cnt[a[j]]--; j--; } } for(int i=j;i>=1;i--) L[i]=1,cnt[a[i]]--; Solve(root); printf("%lld\n",ans); } return 0; }
标算是左偏树,不过用笛卡尔树+倍增也能搞过去:HDU 5575 (Discover Water Tank,2015 ACM/ICPC上海)
首先可以根据隔板的高度,对于$n-1$个隔板建立一个大根笛卡尔树
有了这棵笛卡尔树,我们可以考虑利用它来划分出分治区间
比如,对于笛卡尔树根节点对应原序列的位置$pos_{root}$,相当于将$1\text{~}n$的区间划分成两部分$[1,pos_{root}],[pos_{root}+1,n]$,且每部分的水位最高都不超过$h[pos_{root}]$;其余节点的划分同理
我们先将每个查询分配到划分树上,具体方法是,先倍增出每个划分树节点的父亲关系,然后对于每个查询$\{x,y,w\}$,从$[x,x]$对应的区间,向上找到树上最深的 水位限制大于等于$y$的祖先,并将这个查询扔到那个节点的vector中
于是考虑树形dp
对于一个区间,要不将它整体灌满,要不不灌满、并向下递归;所以对于每个划分树上的节点,分别记录灌满和不灌满的 最多正确询问数
注意$y$的边界即可(我的处理是将每个$y++$)

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; struct Query { int x,y,w; Query(int a,int b,int c) { x=a,y=b,w=c; } }; inline bool operator <(Query A,Query B) { return A.y<B.y; } inline bool operator >(Query A,Query B) { return A.y>B.y; } const int INF=1<<30; const int N=200005; const int LOG=20; int n,m; int h[N]; struct Cartesian { int root; int ls[N],rs[N]; vector<int> v; void clear() { root=0; v.clear(); for(int i=1;i<n;i++) ls[i]=rs[i]=0; } void build() { for(int i=1;i<n;i++) { int j=0; while(v.size() && h[v.back()]<h[i]) { j=v.back(); v.pop_back(); } if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } }tree; int tot; int lb[N],rb[N],lim[N]; int ls[N],rs[N]; int fa[N][LOG]; int place[N]; void Build(int x,int y,int l,int r,int f) { lb[x]=l,rb[x]=r; fa[x][0]=f; if(l==r) { place[l]=x; return; } ls[x]=++tot; lim[tot]=h[y]; Build(tot,tree.ls[y],l,y,x); rs[x]=++tot; lim[tot]=h[y]; Build(tot,tree.rs[y],y+1,r,x); } int sum[N],sub[N]; vector<Query> v[N]; void dfs(int x) { if(ls[x]) dfs(ls[x]); if(rs[x]) dfs(rs[x]); int empty=0,full=0; for(int i=0;i<v[x].size();i++) { Query tmp=v[x][i]; if(tmp.w==0) empty++; } sub[x]=sub[ls[x]]+sub[rs[x]]+empty; for(int i=0;i<v[x].size();) { int j=i; while(j<v[x].size() && v[x][i].y==v[x][j].y) { Query tmp=v[x][j]; if(tmp.w==0) empty--; if(tmp.w==1) full++; j++; } i=j; sub[x]=max(sub[x],sum[ls[x]]+sum[rs[x]]+full+empty); } sum[x]=sum[ls[x]]+sum[rs[x]]+full; } int main() { int T; scanf("%d",&T); for(int kase=1;kase<=T;kase++) { scanf("%d%d",&n,&m); for(int i=1;i<n;i++) scanf("%d",&h[i]); tree.clear(); tree.build(); for(int i=1;i<=tot;i++) { v[i].clear(); ls[i]=rs[i]=fa[i][0]=0; sum[i]=sub[i]=0; } tot=1; lim[1]=INF; Build(1,tree.root,1,n,0); for(int i=1;i<LOG;i++) for(int j=1;j<=tot;j++) fa[j][i]=fa[fa[j][i-1]][i-1]; for(int i=1;i<=m;i++) { int x,y,w; scanf("%d%d%d",&x,&y,&w); Query tmp(x,++y,w); int p=place[x]; for(int j=LOG-1;j>=0;j--) if(fa[p][j] && y>lim[fa[p][j]]) p=fa[p][j]; if(y>lim[p]) p=fa[p][0]; v[p].push_back(tmp); } for(int i=1;i<=tot;i++) sort(v[i].begin(),v[i].end()); dfs(1); printf("Case #%d: %d",kase,sub[1]); putchar('\n'); } return 0; }
一般都是银牌题难度的样子吧,平常见的不多,遇到再补充
Nowcoder 209390 (Sort the String Revision,2020牛客暑期多校第四场)
Yandex Contest 24597H (Longest Loose Segment,2021 PTZ Camp Day4)

Time limit: 2 seconds
Memory limit: 256Mb
A list A is called loose if max(A) + min(A) > len(A).
Today Rikka got a list A of length n. She wants to find the longest segment [l,r] in A
such that list [A_l,A_{l+1},...,A_r] is loose.
Rikka will make m turns with list A. On each turn, Rikka will perform one or more given
operations in sequence. Each operation is swapping two elements in list A. Your task is
to calculate the length of the longest loose segment of A and the resulting list
after each turn.
Note that the operations on turn i are performed on the list that was the result of
turn (i-1).
Input
The first line contains two integers n and m (1<=n<=10^6 and 1<=m<=30).
The second line contains n integers A_i(-10^6<=A_i<=10^6) that consitute the
initial list A.
Then follow m descriptions of the turns. For each turn, the first line contains a single
integer k (1<=k<=10^6), the number of swaps. Then k lines follow: each of them
contains two integers u_i and v_i (1<=u_i,v_i<=n and u_i≠v_i) such that Rikka
will swap A_{u_i} and A_{v_i} in this operation.
It is guaranteed that Sum_{k}<=10^6.
Output
On the first line, output a single integer: the length of the longest loose segment of A.
Then output m lines. On each of them, print a single integer: the length of the longest
loose segment of the resulting list after each turn.
Example
standard input
5 2
1 2 -2 3 4
1
2 3
1
1 2
standard output
2
3
4
在笛卡尔树上用类似线段树的方法在每个节点维护多个值、父节点的值通过子节点合并得到确实是未曾设想的道路...不过想来也很有道理:反正每个节点最多只有两个儿子,并且只要保证每次都完整建树并完整计算一遍(即不能像线段树一样支持修改),那么该做法就是线性的。
在$m$轮中,每一轮都重新建立一棵笛卡尔树并进行dp。在每个笛卡尔树的节点$x$上,除了建树得到的$ls[x],rs[x]$,再额外维护$len[x]$(最长Loose Segment的长度)、$sz[x]$(子树大小,即所包含的区间长度)、$mx[x]$(子树中最大的$a[i]$值)。其中$sz[x],mx[x]$的维护是显然的,而$len[x]$的维护需要一点对于Loose Segment性质的简化。
若在当前区间中最长Loose Segment不经过$x$,那么一定为$max(len[ls],len[rs])$;否则最长Loose Segment的最大$a[i]$的值一定为$max(mx[ls],mx[rs])$,因为区间最小值已经确定为$a[x]$,而区间最大值显然越大越好(从而使得理论长度$mx+mn-1$最大)。设$mx[ls]>mx[rs]$,那么左区间能够延伸到$x$的位置相当于要求$a[x]+mx[ls]-1\geq sz[ls]$,这是因为若$a[x]+mx[ls]-1<sz[ls]$,那么$sz[ls]\geq len[ls]>a[x]+mx[ls]-1$,则最长Loose Segment一定不如左区间中的长。若左区间能延伸到$x$,则有$len[x]=max(a[x]+mx[ls]-1,sz[x])$。

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int oo=1<<30; const int N=1000005; //a的下标从1到n struct Cartesian { int root; int ls[N],rs[N]; vector<int> v; void clear(int n) { root=0; v.clear(); for(int i=1;i<=n;i++) ls[i]=rs[i]=0; } void build(int *a,int n) { clear(n); for(int i=1;i<=n;i++) { int j=0; //a[v.back()]<a[i] 大根 //a[v.back()]>a[i] 小根 while(v.size() && a[v.back()]>a[i]) j=v.back(),v.pop_back(); if(!v.size()) root=i; else rs[v.back()]=i; ls[i]=j; v.push_back(i); } } }t; int n,m; int a[N]; int ans; int len[N],sz[N],mx[N]; inline void dfs(int x) { int ls=t.ls[x],rs=t.rs[x]; if(ls) dfs(ls); if(rs) dfs(rs); sz[x]=sz[ls]+sz[rs]+1; mx[x]=a[x]; len[x]=max(a[x]>0?1:0,max(len[ls],len[rs])); if(mx[ls]<mx[rs]) swap(ls,rs); if(ls) { mx[x]=max(mx[x],mx[ls]); if(a[x]+mx[x]-1>sz[ls]) len[x]=min(a[x]+mx[x]-1,sz[x]); } ans=max(ans,len[x]); } int solve() { t.build(a,n); ans=0; dfs(t.root); return ans; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&a[i]); mx[0]=-oo; printf("%d\n",solve()); while(m--) { int k,x,y; scanf("%d",&k); while(k--) { scanf("%d%d",&x,&y); swap(a[x],a[y]); } printf("%d\n",solve()); } return 0; }
ICPC 2020 EC-Final B
(完)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号