树状数组上二分(logn求第k小)
主要是留个板子免得以后慢慢推。
模板:

//需要满足(1<<_log)>=n,且N>(1<<_log) //多测时注意赋初值 const int N=200005; int t[N],_log; inline int lowbit(int x) { return x&(-x); } inline void add(int k,int x) { for(int i=k;i<N;i+=lowbit(i)) t[i]+=x; } inline int query(int k) { int ans=0; for(int i=k;i;i-=lowbit(i)) ans+=t[i]; return ans; } inline int kth(int k) { int pos=1<<_log; for(int i=_log-1;i>=0;i--) if(t[pos-(1<<i)]>=k) pos-=(1<<i); else k-=t[pos-(1<<i)]; return pos; }
类似在主席树中使用到的 用线段树求区间第$k$小,树状数组也是可以支持类似的操作的。不过由于数据结构的局限性,能够求的是全局第$k$小。
举个例子,当$n=8$,$a=1\ 1\ 4\ 5\ 1\ 4\ 1\ 9$表示数字$1$到$8$分别出现的次数,我们可以建出形状如下的树状数组:
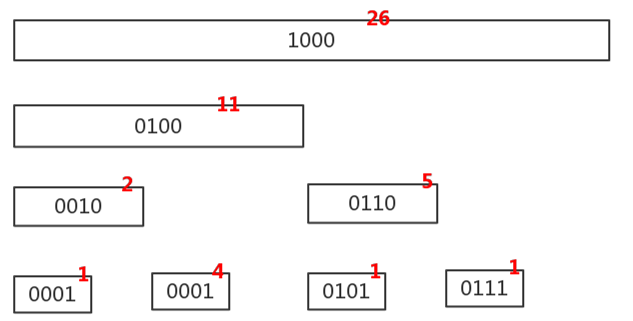
(上面图中,最下面一层的第二个0001应为0011)
其中,每个位置上标红的数值表示对应区间中数字的出现总数。比如,$t[0100]=a_1+a_2+a_3+a_4=1+1+4+5=11$。
同时可以看出,节点$i$所覆盖的区间为$[i-2^{lowbit(i)}+1,i]$、长度为$2^{lowbit(i)}$。比如,$t[0100]$覆盖了区间$[0001,0100]$,$t[0110]$覆盖了区间$[0101,0110]$。
现在考虑找到所有数中从小到大第$14$个数。我们从“根节点”$t[1000]$开始:
1. 类似线段树中二分,我们将其与左儿子$t[0100]$进行比较。能够发现$t[0100]=11<14$,故我们进入右儿子,找其中的第$14-11=3$大。此时右儿子为空,不过我们之后有办法进行处理,不妨先认为有一个节点存在。
2. 再与左儿子$t[0110]$进行比较。能够发现$t[0110]=5\geq 3$,故目标答案在$t[0110]$所包含的区间中,我们进入左儿子$t[0110]$。
3. 再与左儿子$t[0101]$进行比较。能够发现$t[0101]=1<3$,故进入右儿子。这个不存在的右儿子对应的其实就是$0110$。
现在考虑如何处理进入(不存在的)右儿子的情况。
其实我们完全可以不进行任何处理。为什么这样说呢?我们每一步所在的节点,其实都是所在区间的右边界。在上面的例子中,在一开始,$1000$是$0001$到$1000$的右边界;第一步过后,$1000$是$0101$到$1000$的右边界;第二步过后,$0110$是$0101$到$1000$的右边界;第三步后,$0110$是$0110$到$0110$的右边界。在每一步过后,目标答案所在的区间长度就减小了一半,而区间的右边界就是目前的节点编号。
于是我们在寻找全局第$k$小的过程中,只需要如下处理:
1. 在一开始,当前右边界$pos=2^{\lceil logn\rceil}$。必须为$2$的幂次,否则不能保证包含了$[1,n]$的区间。
2. 从高到低确定目标答案的每一位。具体来说,就是将$i$从$\lceil logn\rceil-1$一直循环到$0$。此时左儿子(一定存在)的节点编号为$pos-2^i$,我们将$t[pos-2^i]$与$k$进行比较。
3. 若$t[pos-2^i]\geq k$,则答案为左儿子对应的区间中的第$k$小,故$pos=pos-2^i$、$k$不变;否则答案出现在右儿子对应的区间中,不过是第$k-t[pos-2^i]$小,故$k=k-t[pos-2^i]$、$pos$不变。
inline int kth(int k) { int pos=1<<_log; for(int i=_log-1;i>=0;i--) if(t[pos-(1<<i)]>=k) pos-=(1<<i); else k-=t[pos-(1<<i)]; return pos; }
Nowcoder 5671J (Josephus Transform,2020牛客暑期多校第六场)
包含了一个奇妙的用法:以$O(nlogn)$求约瑟夫环的出队顺序。
首先考虑将树状数组的$[1,n]$位置全部$+1$,表示每个数都是存在的。设上一个被干掉的人编号为$cur$(初始为$0$),在树状数组上二分求出下一个可用的编号$nxt$,其中需要满足$query(nxt)-query(cur)=k$,换句话说也就是求全体区间第$query(cur)+k$小。
若$query(cur)+k>query(n)$,就表示要在环上绕多次,那就相当于求全体区间第$(query(cur)+k-1)\text{%} query(n)+1$小。调用kth函数即可得到编号。
剩余的部分就是对一个排列置换多次了,暴力找出循环节,在每个数都在循环上向后移动$x$次即可得到置换后的排列。

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=200005; int t[N],_log; inline int lowbit(int x) { return x&(-x); } inline void add(int k,int x) { for(int i=k;i<N;i+=lowbit(i)) t[i]+=x; } inline int query(int k) { int ans=0; for(int i=k;i;i-=lowbit(i)) ans+=t[i]; return ans; } inline int kth(int k) { int pos=1<<_log; for(int i=_log-1;i>=0;i--) if(t[pos-(1<<i)]>=k) pos-=(1<<i); else k-=t[pos-(1<<i)]; return pos; } int n,m; int p[N],trans[N],tmp[N]; void gen(int k) { for(int i=1;i<=(1<<_log);i++) t[i]=0; for(int i=1;i<=n;i++) add(i,1); int cur=0; for(int i=1;i<=n;i++) { int npos=query(cur)+k; if(npos>(n-i+1)) npos=(npos-1)%(n-i+1)+1; trans[i]=cur=kth(npos); add(cur,-1); } } int cycle[N],vis[N]; void pw(int x) { for(int i=1;i<=n;i++) vis[i]=-1; for(int i=1;i<=n;i++) { if(vis[i]!=-1) continue; int cur=i,top=0; while(vis[cur]==-1) { vis[cur]=top; cycle[top++]=cur; cur=trans[cur]; } for(int j=0;j<top;j++) trans[cycle[j]]=cycle[(vis[cycle[j]]+x)%top]; } } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) p[i]=i; _log=1; while((1<<_log)<n) _log++; while(m--) { int k,x; scanf("%d%d",&k,&x); gen(k); pw(x); for(int i=1;i<=n;i++) tmp[i]=p[trans[i]]; for(int i=1;i<=n;i++) p[i]=tmp[i]; } for(int i=1;i<=n;i++) printf("%d%c",p[i],i==n?'\n':' '); return 0; }
(其余部分暂时咕咕咕)


