树的一些概念性质
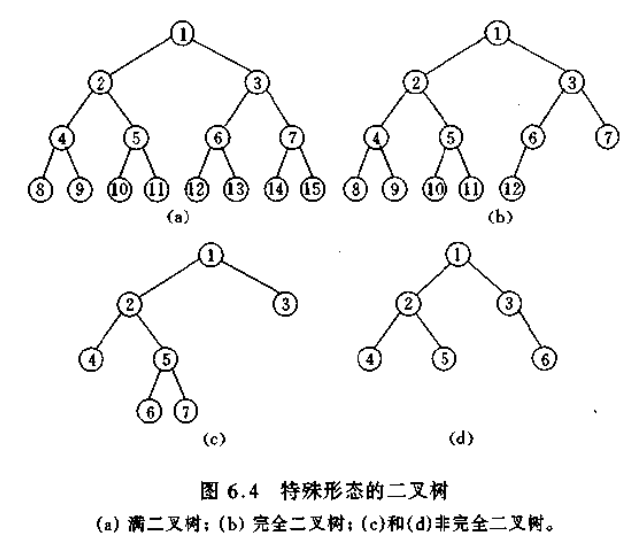
满二叉树:深度为k且有2k-1个节点的二叉树,这种树的特点是每一层上的节点数都是最大节点数
完全二叉树:深度为k,有n个节点的二叉树,叶子结点只在最大两层上出现,左子树深度与右子树深度相等或大1,当且仅当其每一个节点都与深度为k的满二叉树中从编号1至n的结点一一对应时,就是完全二叉树
1.二叉树是度为2的有序树( )
【答案】× 不大于2的有序树

深度为K的完全二叉树的结点个数小于或等于深度相同的满二叉树。
深度:树中节点的最大层次
祖先:是从根节点到该节点所经分支上的所有节点
终端节点:叶子
度:节点拥有的子树数称为节点的度,度为0的节点称为叶子,树的度是树内各节点的度的最大值
叶子节点数=度为2的节点数+1

已知二叉树有50个叶子结点,则该二叉树的总结点数至少是 99, 二叉树共有3类结点,即度为2的结点,度为1的结点和度为0的结点(叶子结点); 任何一个二叉树的叶子结点数总比度为2的结点数多一个;至少的情况就是该二叉树为满二叉树,及没有度为1的结点;
任一棵树中,结点总数=总分支数目+1
例如 .一棵树T中,包括一个度为1的结点,两个度为2的结点,三个度为3的结点,四个度为4的结点和若干叶子结点,则T的叶结点数为 21。
解析 n0+4+3+2+1 = (n0*0 + 1*1 + 2*2 + 3*3 + 4*4)+1 则:n0=21 叶子结点就是21
线索二叉树
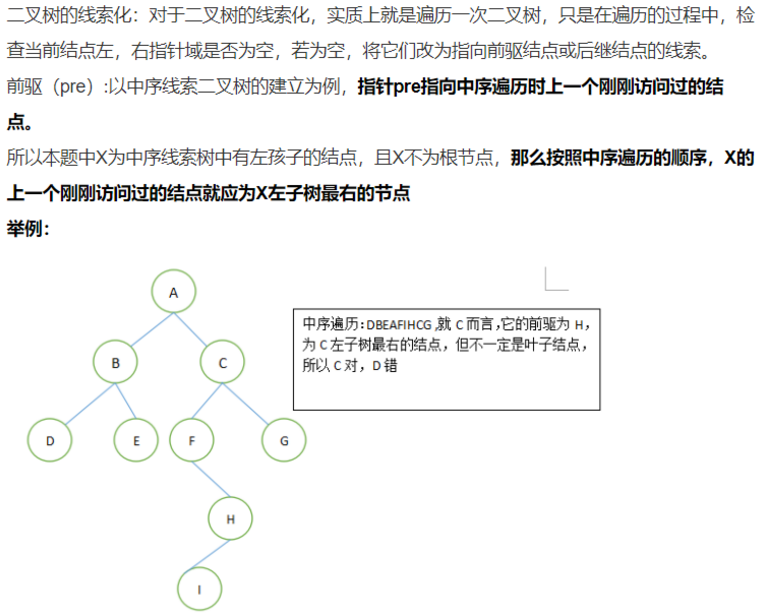
一个二叉树通过如下的方法“穿起来”:所有原本为空的右(孩子)指针改为指向该节点在中序序列中的后继,所有原本为空的左(孩子)指针改为指向该节点的中序序列的前驱。
如果有左空指针则将左空指针指向其前驱,如果有右空指针则将右空指针指向其后继。
lTag rTag是两个标签,当lTag或rTag为0时则lChild和rChild存的是它的左或右孩子,当lTag或rTag为1时lChild和rChild存的是它的前驱或后继

如图将下面的二叉树线索化
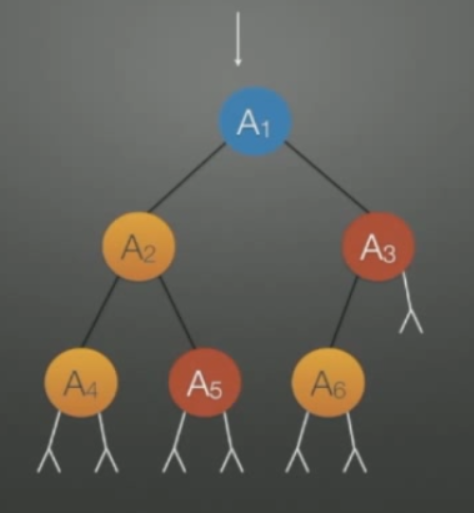

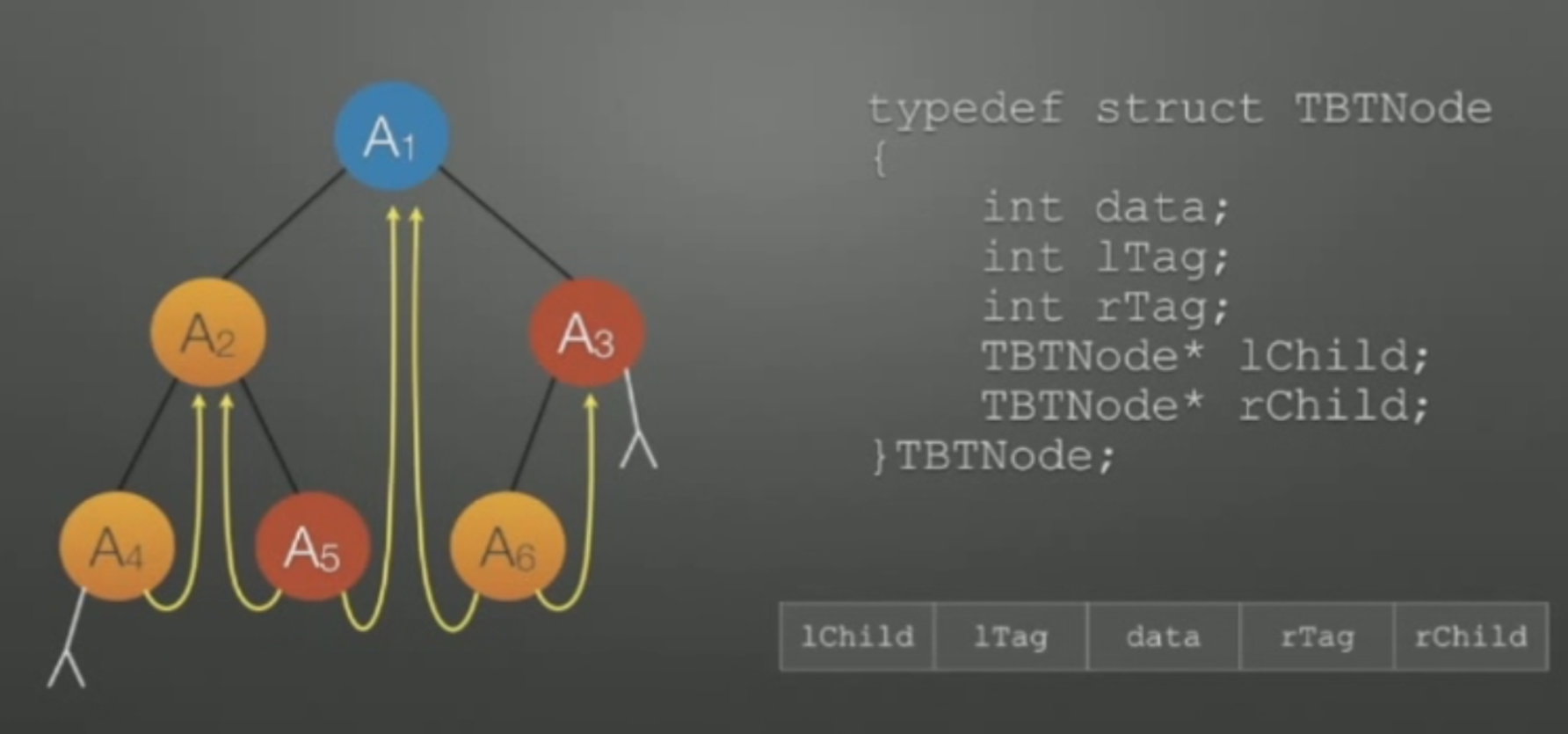

n个结点的线索二叉树上含有的线索数为( )
A)2n B)n-l C)n+l D)n
【答案】C
【解析】线索二叉树是利用二叉树的空链域加上线索,n个结点的二叉树有n+1个空链域。除根节点外,其余n-1个顶点都有父节点,也就占了n-1个链域,一共有2n个链域减去n-1就有n+1个链域
19.设y指向中序二叉线索树的一叶子,x指向一待插入结点,现x作为y的左孩子插入,树中标志域为ltag和rtag,并规定标志为1是线索,则下面的一段算法将x插入并修改相应的线索,试补充完整:(lchild,rchild分别代表左,右孩子)
x->ltag= _____________;
x->lchild= _____________;
y->ltag= _____________;
y->lchild= _____________;
x->rtag= _____________;
x->rchild= _____________;
if (x->lchild!=NULL) && (x->lchild->rtag==1) x->lchild->rchild=_____________;
【答案】(1)1 (2)y->lchild (3)0 (4)x (5)1 (6)y(右指针指向它的后继节点) (7)x(原本y的左孩子的右孩子可能指向的是它的后继节点也就是y,但是这个时候x已经替代了y,那么原来y的左孩子的右孩子的后继节点就应该是x了)
一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反,则该二叉树一定满足(C)
A)所有的结点均无左孩子 B)所有的结点均无右孩子
C)只有一个叶子结点 D)是任意一棵二叉树
解析:先序序列是“根左右”,后序序列是“左右根”,若要这两个序列相反, 只有单支树,单支树的特点是只有一个叶子结点
从中序的规则可知树根在中间,树根的左边是左孩子,右边是右孩子;从后序可知树根为最后一个节点,先序第一个节点为根节点
一棵有n个结点的满二叉树有_____________个度为1的结点,有_____________个分支(非终端)结点和_____________个叶子,该满二叉树的深度为_____________。
【答案】(1)0 (2)(n-1)/2 (3)(n+1)/2 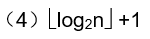
一棵完全二叉树上有1001个结点,其中叶子结点的个数是( )
A)250 B)500 C)505 D)以上答案都不对
【答案】D
【解析】若每个结点均已经编号,则最大的编号为1001,其父亲结点的编号为500,那么从501到1001均为叶子结点。因此,叶子结点数为1001-500=501。故答案为D。不要认为只有最后一层才是叶子节点
已知二叉树有50个叶子结点,则该二叉树的总结点数至少是_____________。
【答案】99
【解析】在二叉树中,N0 = N2+1,所以,有50个叶子结点的二叉树,有49个度为2的结点。若要使该二叉树的结点数最少,度为1的结点应为0个,即总结点数N= N0 +N1+ N2 =99。

注意第11题编号最小的叶子节点不在最后一层而在倒数第二层。
13.有数据WG={7,19,2,6,32,3,21,10},则所建Huffman树的树高是_____________,带权路径长度WPL为_____________。
【答案】(1)6 (2)261(权值乘以高度减一)
n(n大于1)个结点的各棵树中,其深度最小的那棵树的深度是_____________。它共有_____________个叶子结点和_____________个非叶子结点,其中深度最大的那棵树的深度是_____________,它共有_____________个叶子结点和_____________个非叶子结点。
【答案】(1)2 (2)n-1 (3)1 (4)n (5)1 (6)n-1
没有说是二叉树,n-1叉也可以
4.由一棵二叉树的先序序列和后序序列可以惟一确定它( )
【答案】× 例如有两颗二叉树(1)B是A的左孩子 先序 AB 后序 BA(2)B是A 的右孩子 先序 AB 后序 BA
如果知道中序和先序或后序中其中一个就可以唯一确定,因为没有中序不知道左右孩子
二叉链表存储结构
通过改造二叉树的存储结构来存一般的树,对于一般的树,父节点不一定要直接指向每一个孩子节点,也就是如图的转换,父节点的左指针指向其第一个孩子,第一个孩子的右指针指向它的兄弟节点,依次类推下去。

如图是其存储结构

利用二叉链表存储树时,根结点的右指针是( )
A)指向最左孩子 B)指向最右孩子 C)空 D)非空
【答案】C
【解析】利用二叉链表存储树时,即用孩子兄弟链表存储树,根结点的左指针指向其第一子女,根结点的右指针指向其下一兄弟,所以为空。



