第15课——递归的应用实战一汉诺塔、全排列等

递归的数学思想

递归的数学表示

斐波拉契数列递归解法

 

#include <stdio.h>

int fibonacci(int n)
{
    if( n > 1 )
    {
        return fibonacci(n-1) + fibonacci(n-2);
    }
    else if( n == 1 )
    {
        return 1;
    }
    else if( n == 0 )
    {
        return 0;
    }
}

int main()
{
    int i = 0;
    
    for(i=1; i<=10; i++)
    {
        printf("fibonacci(%d) = %d\n", i, fibonacci(i));
    }
    
    return 0;
}

 

运行结果：

 

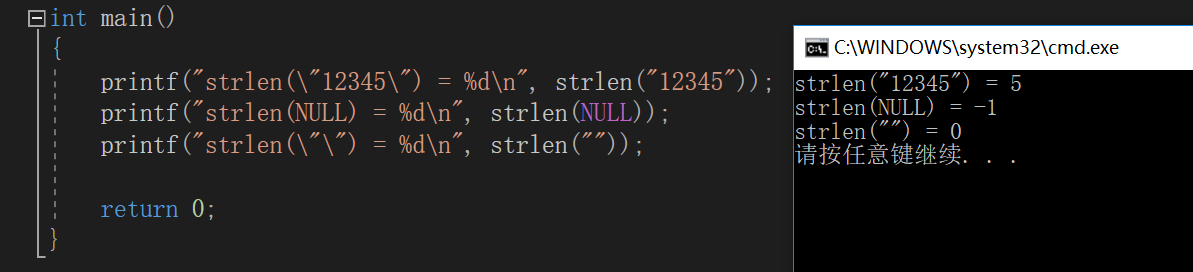
strlen 递归解法

 

#include <stdio.h>

int strlen(const char* s)
{
    if( s == NULL )
    {
        return -1;
    }
    else if( *s == '\0' )
    {
        return 0;
    }
    else
    {
        return strlen(s+1) + 1;
    }
}

int main()
{
    printf("strlen(\"12345\") = %d\n", strlen("12345"));
    printf("strlen(NULL) = %d\n", strlen(NULL));
    printf("strlen(\"\") = %d\n", strlen(""));
    
    return 0;
}

 

运行结果：

 

汉诺塔递归解法

递归当然只能以递归的思路理解，把它展开纯属自讨苦吃。

递归思路，说白了是如下三步：

1、对于问题N，如果N-1已经解决了，那么N是否很容易解决。

2、一步步递推下去，终究会有个“包工头”，接到“搬第一层”的任务。

3、既然第一层搬了，那么第二层当然就可以搬了；第二层搬了，第三层又可以搬了……依次类推，直到第N层。于是问题搞定。 

这一步就是“回归”。 

如上三步加起来，就是“递归”。 

推而广之，任何问题，不管规模为N时有多复杂，只要把N-1那块“外包”给别人做之后，我们在这个基础上可以轻易完成N，那么它很可能就适合用“递归”解决。

那么，怎么最终确定它能不能用“递归”做呢？

看当N取1或2之类最简情况时，问题是否可以解决——然后写程序解决它。

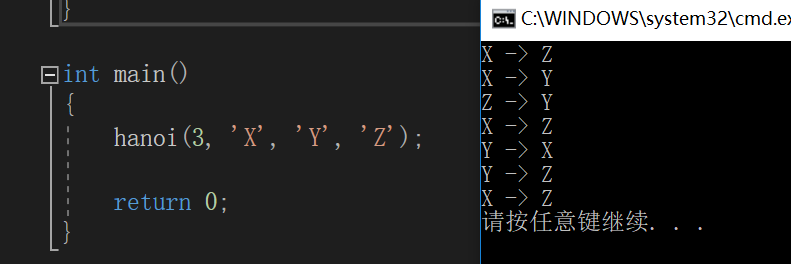
#include <stdio.h>

void hanoi(int n, char a, char b, char c) //a借助b移到C
{
    if( n > 0 )
    {
        if( n == 1 )
        {
            printf("%c -> %c\n", a, c); //一个盘子，从起点a移到终点c
        }
        else
        {
            hanoi(n-1, a, c, b);  //把头上的n-1个盘子从起点a借助c移到b
            
            printf("%c -> %c\n", a, c); //把n个盘子从起点a移到终点c
            
            hanoi(n-1, b, a, c); //把n-1个盘子从b借助a移到c
        }
    }
}

int main()
{
    hanoi(3, 'X', 'Y', 'Z');
    
    return 0;
}

运行结果如下：

全排列递归解法

 全排列函数：

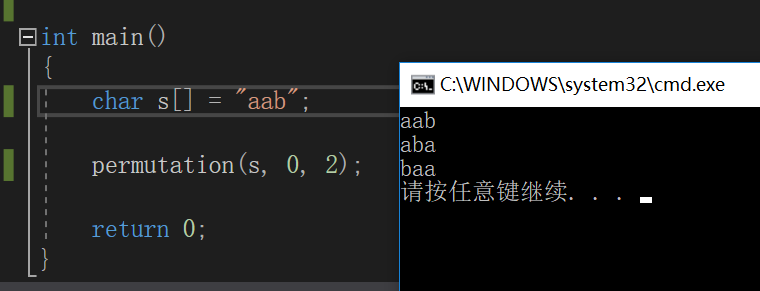
void permutation(char s[], int b, int e)
{
    if( (0 <= b) && (b <= e) )
    {
        if( b == e )
        {
            printf("%s\n", s);
        }
        else
        {
            int i = 0;
            
            for(i=b; i<=e; i++)
            {
                char c = s[b];
                s[b] = s[i];
                s[i] = c;
                
                permutation(s, b+1, e);
                
                c = s[b];
                s[b] = s[i];
                s[i] = c;
            }
        }
    }
}

main函数及运行结果

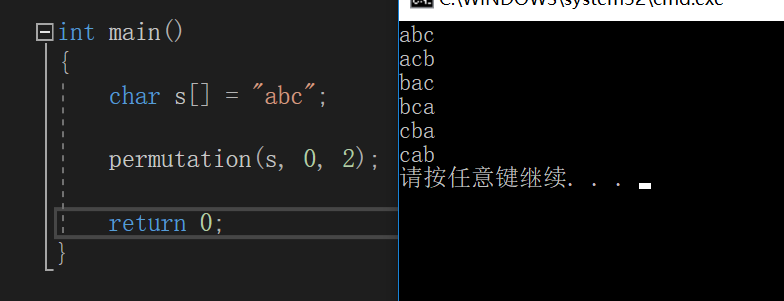
“abc”传入全排列函数，首先b=0；‘a’和自身交换，剩下的“bc”进行全排列，

然后是“ab”交换位置，b在前，“ac”进行全排列，把交换后的“bc”还原。

最后“ac”交换位置，c在前，“ba”进行全排列，把交换后的“ac”还原。

修改全排列元素：为"abb"

运行结果如下：

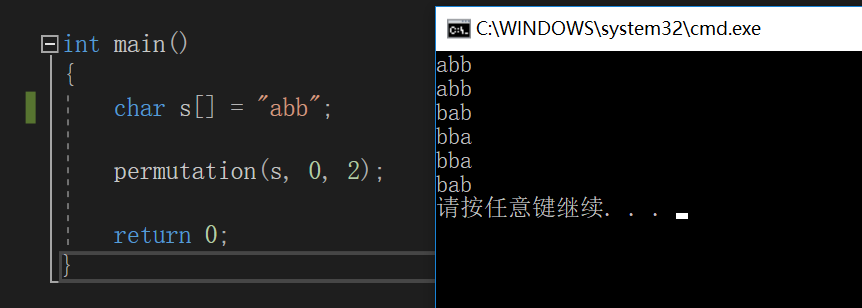
可以看到，全排列的结果有重复，此排列函数不能处理有重复元素的全排列。

怎样修改代码呢？

当判断到重复的元素后就不交换，即要执行交换，必须当前的两元素不同才交换。

修改代码为：

_Bool isSwap(char *s, int b, int e)
{
    for (int i = b; i < e; i++)
    {
        if(s[i] == s[e])
          return 0;
    }
    return 1;

}

void permutation(char *s, int b, int e)
{
    if( (0 <= b) && (b <= e) )
    {
        if( b == e )
        {
            printf("%s\n", s);
        }
        else
        {
            int i = 0;
            
            for(i=b; i<=e; i++)
            {
                if (isSwap(s, b, i))
                {
                    char c = s[b];
                    s[b] = s[i];
                    s[i] = c;

                    permutation(s, b + 1, e);

                    c = s[b];
                    s[b] = s[i];
                    s[i] = c;
                }
                
            }
        }
    }
}

运行结果如下：

小结：