第13课——栈的应用实战

几乎所有的编译器都具有检测括号是否匹配的能力

编译器中的括号检测能力是如何实现的呢？

匹配函数：

int match(char left, char right)
{
    int ret = 0;
    
    switch(left)
    {
        case '<':
            ret = (right == '>');
            break;
        case '(':
            ret = (right == ')');
            break;
        case '[':
            ret = (right == ']');
            break;
        case '{':
            ret = (right == '}');
            break;
        case '\'':
            ret = (right == '\'');
            break;
        case '\"':
            ret = (right == '\"');
            break;
        default:
            ret = 0;
            break;
    }
    
    return ret;
}

 代码复用链式栈的，main函数更改如下：

#include <stdio.h>
#include <stdlib.h>
#include "LinkStack.h"

/* run this program using the console pauser or add your own getch, system("pause") or input loop */

int isLeft(char c)
{
    int ret = 0;
    
    switch(c)
    {
        case '<':
        case '(':
        case '[':
        case '{':
        case '\'':
        case '\"':
            ret = 1;
            break;
        default:
            ret = 0;
            break;
    }
    
    return ret;
}

int isRight(char c)
{
    int ret = 0;
    
    switch(c)
    {
        case '>':
        case ')':
        case ']':
        case '}':
        case '\'':
        case '\"':
            ret = 1;
            break;
        default:
            ret = 0;
            break;
    }
    
    return ret;
}

int match(char left, char right)
{
    int ret = 0;
    
    switch(left)
    {
        case '<':
            ret = (right == '>');
            break;
        case '(':
            ret = (right == ')');
            break;
        case '[':
            ret = (right == ']');
            break;
        case '{':
            ret = (right == '}');
            break;
        case '\'':
            ret = (right == '\'');
            break;
        case '\"':
            ret = (right == '\"');
            break;
        default:
            ret = 0;
            break;
    }
    
    return ret;
}

int scanner(const char* code)
{
    LinkStack* stack = LinkStack_Create();
    int ret = 0;
    int i = 0;
    
    while( code[i] != '\0' )
    {
        if( isLeft(code[i]) )
        {
            LinkStack_Push(stack, (void*)(code + i));
        }
        
        if( isRight(code[i]) )
        {
            char* c = (char*)LinkStack_Pop(stack);
            
            if( (c == NULL) || !match(*c, code[i]) )
            {
                printf("%c does not match!\n", code[i]);
                ret = 0;
                break;
            }
        }
        
        i++;
    }
    
    if( (LinkStack_Size(stack) == 0) && (code[i] == '\0') )
    {
        printf("Succeed!\n");
        ret = 1;
    }
    else
    {
        printf("Invalid code!\n");
        ret = 0;
    }
    
    LinkStack_Destroy(stack);
    
    return ret;
}

int main(int argc, char *argv[])
{
    const char* code = "#include <stdio.h> int main() { int a[5][5]; int (*p)[4]; p = a[0]; printf(\"%d\\n\", &p[3][3] - &a[3][3]); return 0; }";
    
    scanner(code);
    
    return 0;
}

实例二：用栈实现计算：

后缀表达式：

中缀或后缀？

中缀表达式符合人类的阅读和思维习惯；

后缀表达式符合计算机的“运算习惯”；

如何将中缀表达式转化为后缀表达式？

解决方案

 

算法框架

算法实现：

数字判断，操作符判断，左括弧、右括弧判断，优先级判断，输出函数实现如下：

int isNumber(char c)
{
    return ('0' <= c) && (c <= '9');
}

int isOperator(char c)
{
    return (c == '+') || (c == '-') || (c == '*') || (c == '/');
}

int isLeft(char c)
{
    return (c == '(');
}

int isRight(char c)
{
    return (c == ')');
}

int priority(char c)
{
    int ret = 0;
    
    if( (c == '+') || (c == '-') )
    {
        ret = 1;
    }
    
    if( (c == '*') || (c == '/') )
    {
        ret = 2;
    }
    
    return ret;
}

void output(char c)
{
    if( c != '\0' )
    {
        printf("%c", c);
    }
}

中缀转后缀函数：

void transform(const char* exp)
{
    LinkStack* stack = LinkStack_Create();
    int i = 0;
    
    while( exp[i] != '\0' )
    {
        if( isNumber(exp[i]) )
        {
            output(exp[i]);
        }
        else if( isOperator(exp[i]) )
        {
            while( priority(exp[i]) <= priority((char)(int)LinkStack_Top(stack)) )
            {
                output((char)(int)LinkStack_Pop(stack));
            }
            
            LinkStack_Push(stack, (void*)(int)exp[i]);
        } 
        else if( isLeft(exp[i]) )
        {
            LinkStack_Push(stack, (void*)(int)exp[i]);
        } 
        else if( isRight(exp[i]) )
        {
            char c = '\0';
            
            while( !isLeft((char)(int)LinkStack_Top(stack)) )
            {
                output((char)(int)LinkStack_Pop(stack));
            }
            
            LinkStack_Pop(stack);
        }
        else
        {
            printf("Invalid expression!");
            break;
        }        
        i++;
    }
    
    while( (LinkStack_Size(stack) > 0) && (exp[i] == '\0') )
    {
        output((char)(int)LinkStack_Pop(stack));
    }    
    LinkStack_Destroy(stack);
}

main函数及运行结果如下：

 

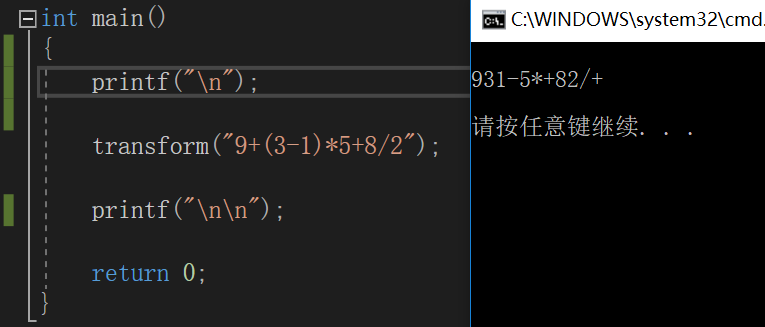
中缀转后缀完成，那计算机是怎样基于后缀表达式进行计算的呢？

解决方案：

算法框架：

 

数字的判断，操作符的判断，执行操作函数。

int isNumber(char c)
{
    return ('0' <= c) && (c <= '9');
}

int isOperator(char c)
{
    return (c == '+') || (c == '-') || (c == '*') || (c == '/');
}

int value(char c)
{
    return (c - '0');
}

int express(int left, int right, char op)
{
    int ret = 0;
    
    switch(op)
    {
        case '+':
            ret = left + right;
            break;
        case '-':
            ret = left - right;
            break;
        case '*':
            ret = left * right;
            break;
        case '/':
            ret = left / right;
            break;
        default:
            break;
    }
    
    return ret;
}

计算函数实现：

int compute(const char* exp)
{
    LinkStack* stack = LinkStack_Create();
    int ret = 0;
    int i = 0;
    
    while( exp[i] != '\0' )
    {
        if( isNumber(exp[i]) )
        {
            LinkStack_Push(stack, (void*)value(exp[i]));
        }
        else if( isOperator(exp[i]) )
        {
            int right = (int)LinkStack_Pop(stack);
            int left = (int)LinkStack_Pop(stack);
            int result = express(left, right, exp[i]);
            
            LinkStack_Push(stack, (void*)result);
        }
        else
        {
            printf("Invalid expression!");
            break;
        }
        
        i++;
    }
    
    if( (LinkStack_Size(stack) == 1) && (exp[i] == '\0') )
    {
        ret = (int)LinkStack_Pop(stack);
    } 
    else 
    {
        printf("Invalid expression!");
    }
    
    LinkStack_Destroy(stack);
    
    return ret;
}

main函数及运行结果如下：

 

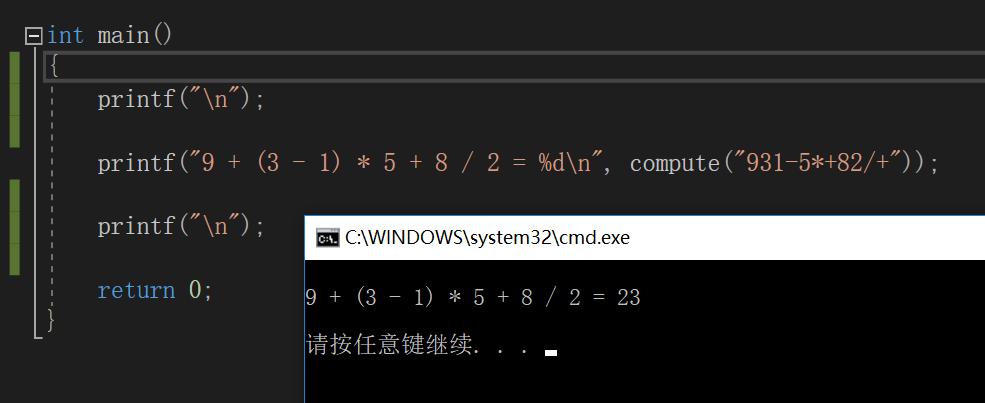
小结：