PCA主成分分析
PCA主成分分析
(一)实验目的
- 理解主成分分析的基本原理;
- 掌握主成分分析模型的设计。
(二)实验条件
-
硬件环境
处理器:lntel(R) Core(TM) i5-8300H CPU @2.30GHz 2.30 GHz
已安装的内存(RAM):8.00 GB (7.85GB可用)、
系统类型:64位操作系统,基于x64的处理器
显卡:GTX1050
-
软件环境
Windows 10专业版、python3.7、PyCharm
(三)算法基本思想
PCA(Principal Component Analysis),即主成分分析方法,是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴,新的坐标轴的选择与数据本身是密切相关的。其中,第一个新坐标轴选择是原始数据中方差最大的方向,第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推,可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴,大部分方差都包含在前面k个坐标轴中,后面的坐标轴所含的方差几乎为0。于是,我们可以忽略余下的坐标轴,只保留前面k个含有绝大部分方差的坐标轴。这相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为0的特征维度,实现对数据特征的降维处理。
基本步骤:
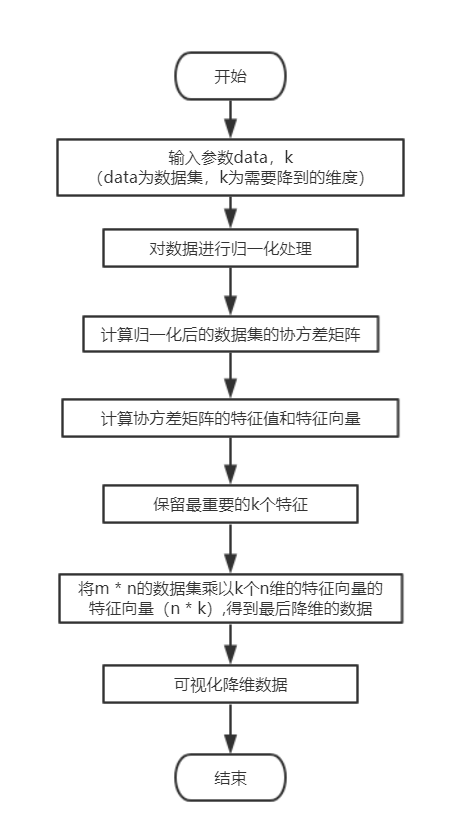
1.对数据进行归一化处理(代码中直接减去均值)
2.计算归一化后的数据集的协方差矩阵
3.计算协方差矩阵的特征值和特征向量
4.保留最重要的k个特征(通常k要小于n)
5.找出k个特征值相应的特征向量
6.将m * n的数据集乘以k个n维的特征向量的特征向量(n * k),得到最后降维的数据。
(四)算法流程图
(五)实验数据
随机创建不同二维数据集作为训练集(至少两组),使用主成分分析进行降维(降到一维)并可视化。
(六)实验结果
-
代码(有必要的注释)
# -*- coding: utf-8 -*- # @Time : 2020/12/17 # @Author : Littleeegg # @File : PCA.py # @Software: PyCharm import numpy import re import matplotlib.pyplot as plt def createData(n): #随机生成训练集并写入文件中 numpy.set_printoptions(suppress=True) #关闭科学计数法输出 all_points = numpy.random.randn(n,2)*10 #生成n个2维数组 # all_points = numpy.random.randn(n,3)*10 #生成n个3维数组 #print(all_points) try: f = open("pca_data.txt","w") try: f.write(str(all_points)) print("-----随机数据集创建成功-----") finally: f.close() except Exception as ex: print("-----出现异常",ex,"-----") def loadData(inFile): # 载入测试数据集 try: f = open(inFile,'r',encoding='utf-8') try: inData = f.readlines() data = list() for line in inData: line = line.replace('[','').replace(']','').strip()#去除文件中的'['和‘]’符号和开头与结尾的空格 strList = re.split('[ ]+',line) #以空格为分割符,分割每一行数据 #print(strList) numList = list() for item in strList: numList.append(float(item)) #print(numList) data.append(numList) #print(data) print("-----数据集加载成功-----") return data finally: f.close() except Exception as ex: print("-----出现异常",ex,"-----") def PCA(data,k): #PCA算法 data = numpy.mat(data) average = numpy.mean(data,axis=0) #求每个特征的平均值 axis=0表示依照列来求均值。假设输入list,则axis=1 norm_data = data - average #规范化 cov_matrix = numpy.cov(norm_data,rowvar=0) #计算协方差矩阵 eig_val,eig_vec = numpy.linalg.eig(numpy.mat(cov_matrix)) #求解协方差矩阵的特征值和特征向量 val_sorted = numpy.argsort(eig_val) #根据特征值大小,从小到大排序 val_choose = val_sorted[:-(k+1):-1] #从后往前取k个特征值,即特征值的从大到小排列 vec_choose = eig_vec[:,val_choose] #返回排序后特征值对应的特征向量(主成分) if k >= len(eig_val): print("k 必须小于特征值的总数" + str(len(eig_val))) return else: low_data = norm_data * vec_choose #将原始数据投影到主成分上得到新的低维数据 new_data = low_data * vec_choose.T + average #获得重构数据 return low_data,new_data def ShowPCA(data,new_data): plt.scatter(numpy.array(data)[:,0],numpy.array(data)[:,1],c='skyblue') plt.scatter(numpy.array(new_data)[:,0],numpy.array(new_data)[:,1],c="red") # plt.plot(numpy.array(new_data)[:,0],numpy.array(new_data)[:,1],color="pink")#画直线的 plt.show() def ShowPCA3D(data,new_data): ax1 = plt.axes(projection='3d') for node in data: ax1.scatter3D(node[0],node[1],node[2],c = 'skyblue') ax1.scatter3D(numpy.array(new_data)[:,0],numpy.array(new_data)[:,1],numpy.array(new_data)[:,2],alpha=0.3,c="red",cmap='winter') plt.show() if __name__ == '__main__': data = createData(150) #随机创建数据集 data = loadData("pca_data.txt") #加载数据集 low_data,new_data = PCA(data,1) ShowPCA(data,new_data) # low_data,new_data = PCA(data,2) # ShowPCA3D(data,new_data) -
数据记录
数据集1:150个二维随机数据、数据集2:150个二维随机数据
-
结果及分析
数据集1降维后 数据集2降维后
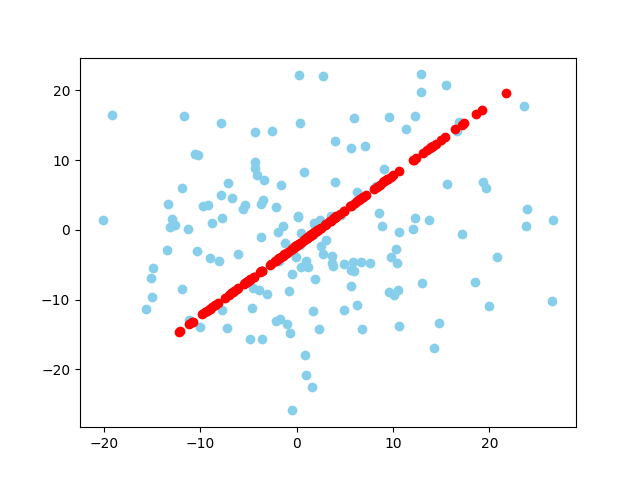
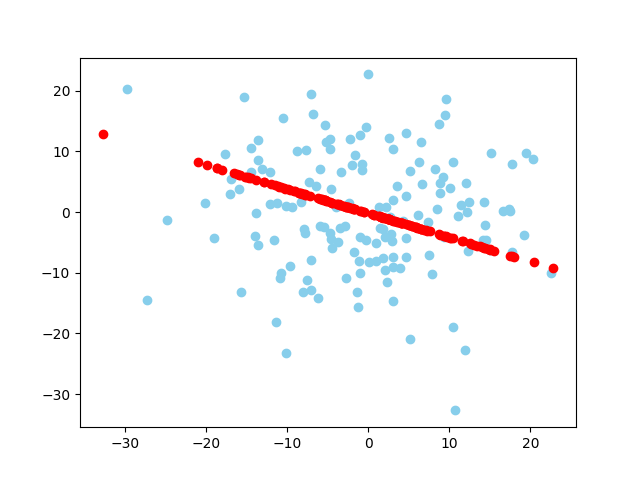
要求是用二维数据的,我因为想试试三维的,就也尝试了一下,但是因为三维平面不会画,百度总奇奇怪怪的,就没有做更好看的了。直接看生成的图可能觉得看不太出来,但是三维图可以拖动旋转,当旋转到一定程度的时候,可以看出,降到2维后的数据确实是一个平面。
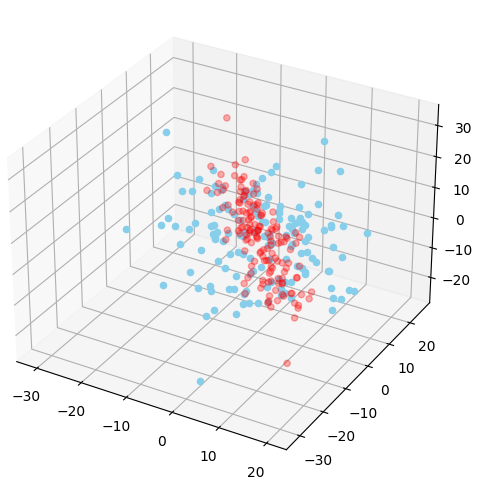

降到2维:旋转前 降到2维:旋转后

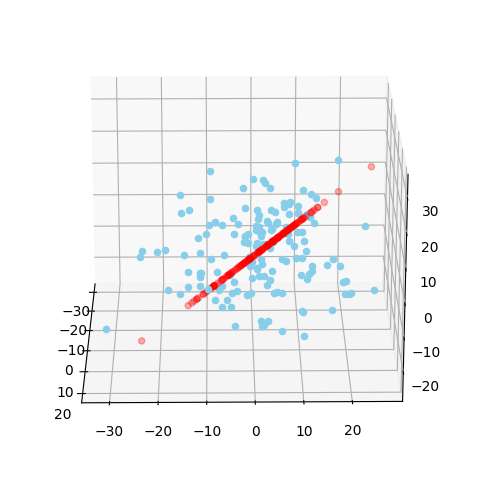
降到1维:旋转前 降到1维:旋转后
-
总结与反思
实验中我更加理解了PCA的主要思想和其意义,主成分分析(principal component analysis)就是一种数据降维方法,其目的是在“信息”损失较小的前提下,将高维的数据转换到低维,从而减小计算量,他的本质就是找一些投影方向,使得数据在这些投影方向上的方差最大,而且这些投影方向是相互正交的。
实验结果还是很成功的,在尝试了二维数据集的情况下也尝试了三维的,更加有感觉了。虽然在写的过程中遇到了很多问题,比如说list和array搞混了啊什么的,特别是特征值排序的时候,用sort函数出问题,报错:ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all();我改来改去还是有问题,后面就用numpy.argsort()函数了,也挺好用的。另外就是画三维图的时候,打算画平面,但是报错z必须要是二维数据的错误,百度了还是稀里糊涂,就自己手动转着看了。
又学到了很多东西,nice~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号