C均值聚类

（一）实验目的

加深对无监督学习的理解和认识；
加深对判别性概念的理解；
掌握C均值聚类算法的设计。

（二）实验条件

硬件环境

Windows10
软件环境

python3.7

（三）算法基本思想

C均值聚类算法是一种简单的迭代型聚类算法，采用距离作为相似性指标，从而发现给定数据集中的C个类，且每个类有一个聚类中心，即质心，每个类的质心是根据类中所有值的均值得到。对于给定的一个包含n个d维数据点的数据集X以及要分得的类别K,选取欧式距离作为相似度指标。聚类目标是使得各类的聚类平方和最小，即最小化：

\[J=\sum_{k=1}^{k} \sum_{i=1}^{n}\left \| u_i-u_k \right \| ^2 \]

欧氏距离计算公式：

\[d(x,z)=\left \| x-z \right \| =\sqrt{ {\textstyle \sum_{d=1}^{D}} (x_d-z_d)^2} \]

简单来说：取定C个类别和选取C个初始聚类中心，按最小距离原则将各模式分配到C类中的某一类，不断地计算类心和调整各模式的类别使每个模式特征矢量到其所属类别的距离平方之和最小。

C-means是一个反复迭代的过程，算法分为四个步骤：

选取数据空间中的C个对象作为初始中心，每个对象代表一个聚类中心；
对于样本中的数据对象，根据它们与这些聚类中心的欧氏距离，按距离最近的准则将它们分到距离它们最近的聚类中心（最相似）所对应的类；
更新聚类中心：将每个类别中所有对象所对应的均值作为该类别新的聚类中心，计算目标函数的值；
判断聚类中心和目标函数的值是否发生改变，若不变，则输出结果，若改变，则返回步骤2。

（四）算法流程图

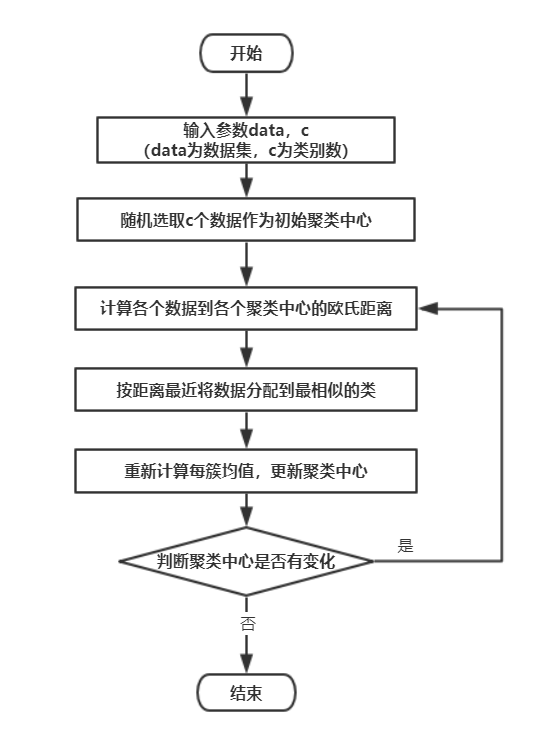
（五）实验数据

随机创建不同二维数据集作为训练集，使用C均值进行聚类展示。

数据集1：100个数据的随机二维数据集

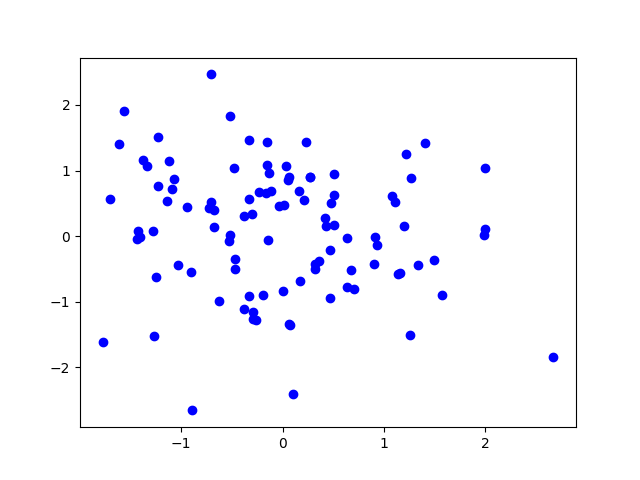
数据集2：200个数据的随机二维数据集

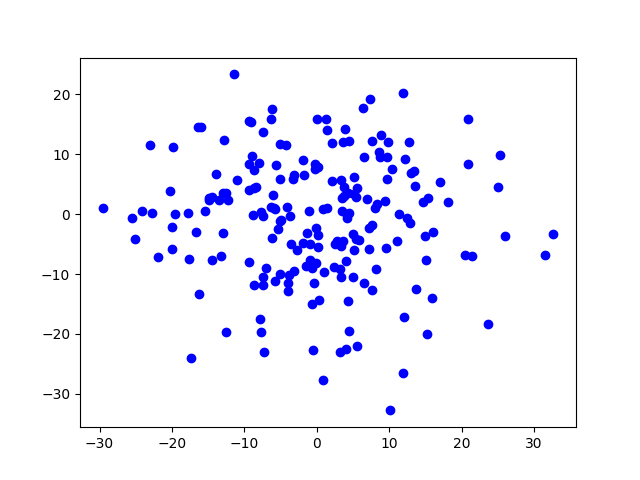
（六）实验结果

代码（有必要的注释）

# -*- coding: utf-8 -*-
# @Time    : 2020/12/5
# @Author  : Littleegg
# @File    : C-means.py
# @Software: PyCharm

import numpy
import re
import random
import matplotlib.pyplot as plt

def calDistance(vec1,vec2):
    #计算向量vec1和向量vec2之间的欧氏距离
    return numpy.sqrt(numpy.sum(numpy.square(vec1-vec2)))

def createData(n):               #随机生成训练集并写入文件中
    numpy.set_printoptions(suppress=True)   #关闭科学计数法输出
    all_points = numpy.random.randn(n,2)*10   #生成n个2维数组
    #print(all_points)
    try:
        f = open("Data.txt","w")
        try:
            f.write(str(all_points))
            print("-----随机数据集创建成功-----")
        finally:
            f.close()
    except Exception as ex:
        print("-----出现异常",ex,"-----")

def loadData(inFile):
    # 载入测试数据集
    try:
        f = open(inFile,'r',encoding='utf-8')
        try:
            inData = f.readlines()
            data = list()
            for line in inData:
                line = line.replace('[','').replace(']','').strip()#去除文件中的'['和‘]’符号和开头与结尾的空格
                #本来想拿正则匹配的，然后失败了哈哈哈哈哈
                strList = re.split('[ ]+',line) #以空格为分割符，分割每一行数据
                #print(strList)
                numList = list()
                for item in strList:
                    numList.append(float(item))
                    #print(numList)
                data.append(numList)
            #print(data)
            print("-----数据集加载成功-----")
            return data
        finally:
            f.close()
    except Exception as ex:
        print("-----出现异常",ex,"-----")

def initCentroids(data,c):
    #随机初始化c个聚类中心
    return random.sample(data,c)    # 返回data中的k个随机数据项

def getClusterDict(data,centroids):
    #对于样本中的数据对象，根据它们与这些聚类中心的欧氏距离，按距离最近的准则将它们分到距离它们最近的聚类中心（最相似）所对应的类
    clusterDict = dict()    #dict() 函数创建一个字典,用来保存簇类结果
    c = len(centroids)
    for node in data:
        #计算节点node与c个质心的距离，选取最近的，并加入相应簇类
        clusterID = -1  #簇分类标记，记录与相应簇距离最近的那个簇
        minDis = float('inf')   #初始化为最大值
        for id in range(c):
            centroid = numpy.array(centroids[id])    #质心
            disctance = calDistance(numpy.array(node),centroid)
            if disctance < minDis:
                minDis = disctance
                clusterID = id

        if clusterID not in clusterDict.keys(): #簇标记不存在，进行初始化
            clusterDict[clusterID] = list()
        clusterDict[clusterID].append(node)     #将node加入对应簇中

    return clusterDict

def getCentroids(clusterDict):
    #重新计算c个质心
    newCentroids = list()
    for id in clusterDict.keys():
        newCentroid = numpy.mean(clusterDict[id],axis=0)    # 计算每列的均值，即找到质心
        newCentroids.append(newCentroid)
    return newCentroids

def getVariance(centroids,clusterDict):
    #计算每个簇类的方差，各个节点到质心的距离累加求和
    sum = 0.0
    for id in clusterDict.keys():
        centroid = numpy.array(centroids[id])
        distance = 0.0
        for node in clusterDict[id]:
            distance += calDistance(numpy.array(node),centroid)
        sum += distance
    return sum

def showCluster(centroids,clusterDict):
    #展示聚类结果
    color_mark = ['deepskyblue','red','lime','orange','purple','pink','black','magenta','gold','cyan']
    node_mark = ['.','^','*','4','d','s','1','2','3','D']
    for key in clusterDict.keys():
        plt.plot(centroids[key][0],centroids[key][1],node_mark[key],color = color_mark[key],markersize = 12)
        for node in clusterDict[key]:
            plt.plot(node[0],node[1],node_mark[key],color = color_mark[key],markersize = 6)
    plt.show()

def C_means(data,c):
    #C-means反复迭代
    centroids = initCentroids(data,c)   #初始化质心
    print("初始质心为：",centroids)
    clusterDict = getClusterDict(data,centroids)    #分类
    new_var = getVariance(centroids,clusterDict)    #计算方差
    old_var = 1     #存储旧的方差
    count = 0       #迭代次数
    while abs(new_var-old_var) >= 1e-6: #退出迭代的条件
        centroids = getCentroids(clusterDict)   #更新聚类中心
        clusterDict = getClusterDict(data,centroids)    #更新分类字典
        old_var = new_var;
        new_var = getVariance(centroids,clusterDict)    #更新方差
        count += 1
        print("第"+str(count)+"次迭代\n"+"本次质心为：" + str(centroids))
        #plt.subplot(4,4,count)
        showCluster(centroids,clusterDict)  #展示聚类结果
    print("最终质心为：",centroids)
    #plt.show()

def showRawData(data):
    #展示原始数据集
    for node in data:
        plt.plot(node[0],node[1],'ob',markersize = 6)
    plt.show()

if __name__ == '__main__':
    createData(200);    #随机创建数据集
    data = loadData("Data.txt");    #加载数据集
    showRawData(data)   #展示原始数据集
    c = int(input("请输入所需类别数（c值）："))     #获取c值
    C_means(data,c)     #C均值聚类
    print("C均值聚类完成！")

数据记录

数据集1：

-----随机数据集创建成功-----
-----数据集加载成功-----
请输入所需类别数（c值）：3
初始质心为： [[-7.49892675, 1.2217541], [-5.72819423, -0.29514288], [9.34052303, -9.22793505]]
第1次迭代
本次质心为：[array([ 8.84693664, -6.74841696]), array([-7.74117618, 7.67519934]), array([-1.66832518, -0.20930931])]

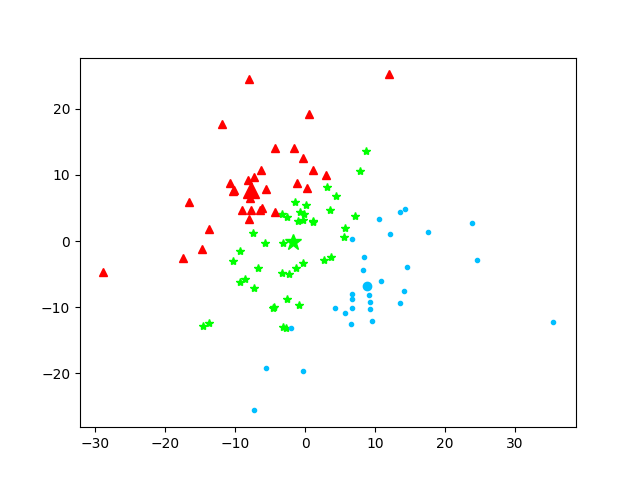
第2次迭代
本次质心为：[array([-1.84963442, -1.20335802]), array([-6.9855816 , 8.63701949]), array([ 9.92518836, -7.19357685])]

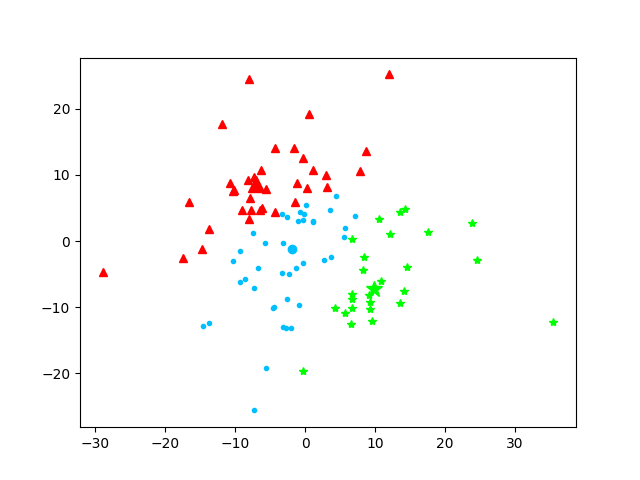
第3次迭代
本次质心为：[array([-2.7245519 , -3.64506266]), array([-5.6259983 , 8.74923299]), array([11.64207775, -5.78893222])]

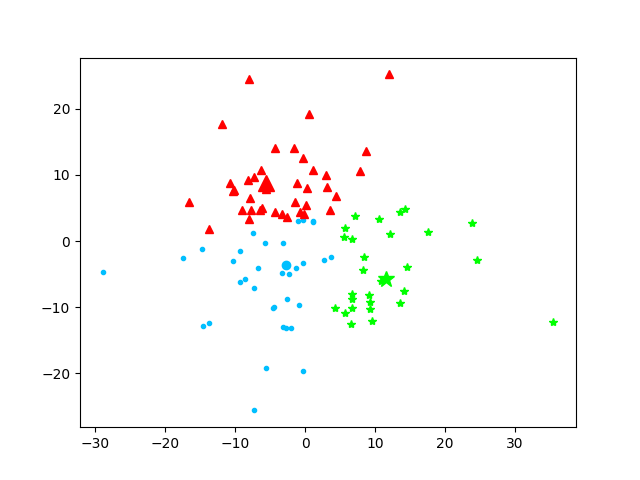
第4次迭代
本次质心为：[array([-5.60154052, -6.28075608]), array([-3.38134735, 8.92486523]), array([11.47755642, -4.44428552])]

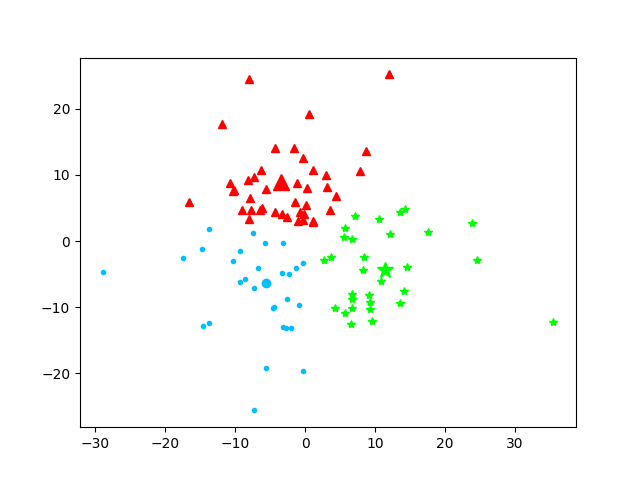
第5次迭代
本次质心为：[array([-7.30021091, -7.53245679]), array([-2.7729317 , 8.51901052]), array([10.92747731, -4.32263358])]

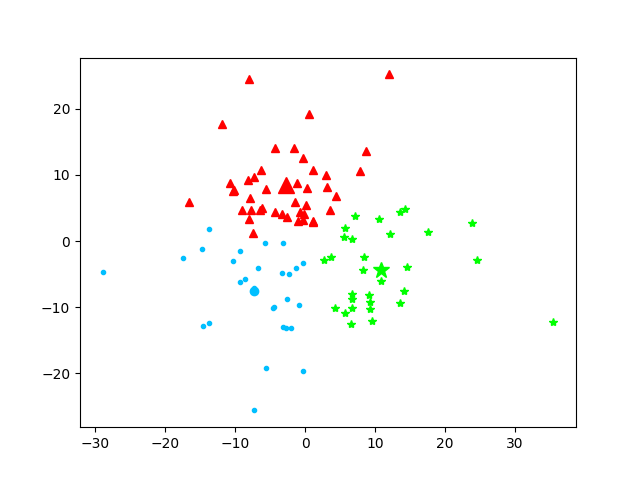
第6次迭代
本次质心为：[array([-7.29311392, -7.84510717]), array([-2.88545539, 8.34526632]), array([10.92747731, -4.32263358])]

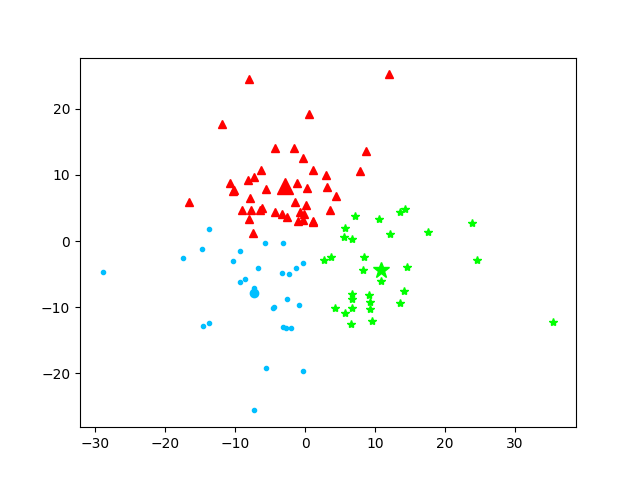
第7次迭代
本次质心为：[array([-7.29311392, -7.84510717]), array([-2.88545539, 8.34526632]), array([10.92747731, -4.32263358])]

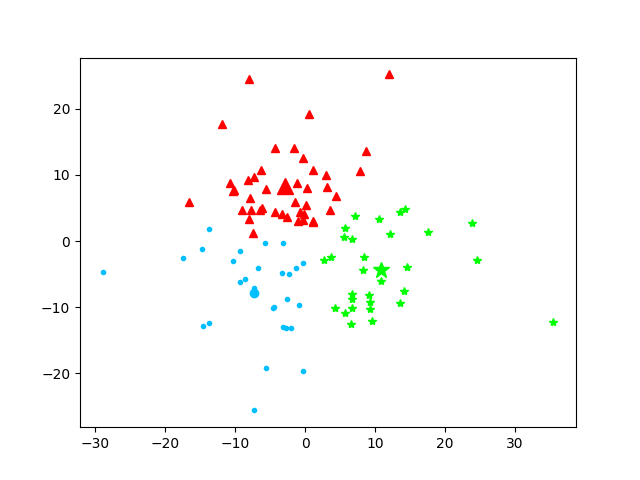
最终质心为： [array([-7.29311392, -7.84510717]), array([-2.88545539, 8.34526632]), array([10.92747731, -4.32263358])]
C均值聚类完成！

数据集2：

因为一张一张图显示保存在麻烦了，聚类结果我就用plt.subplot()函数整在一张图片上了

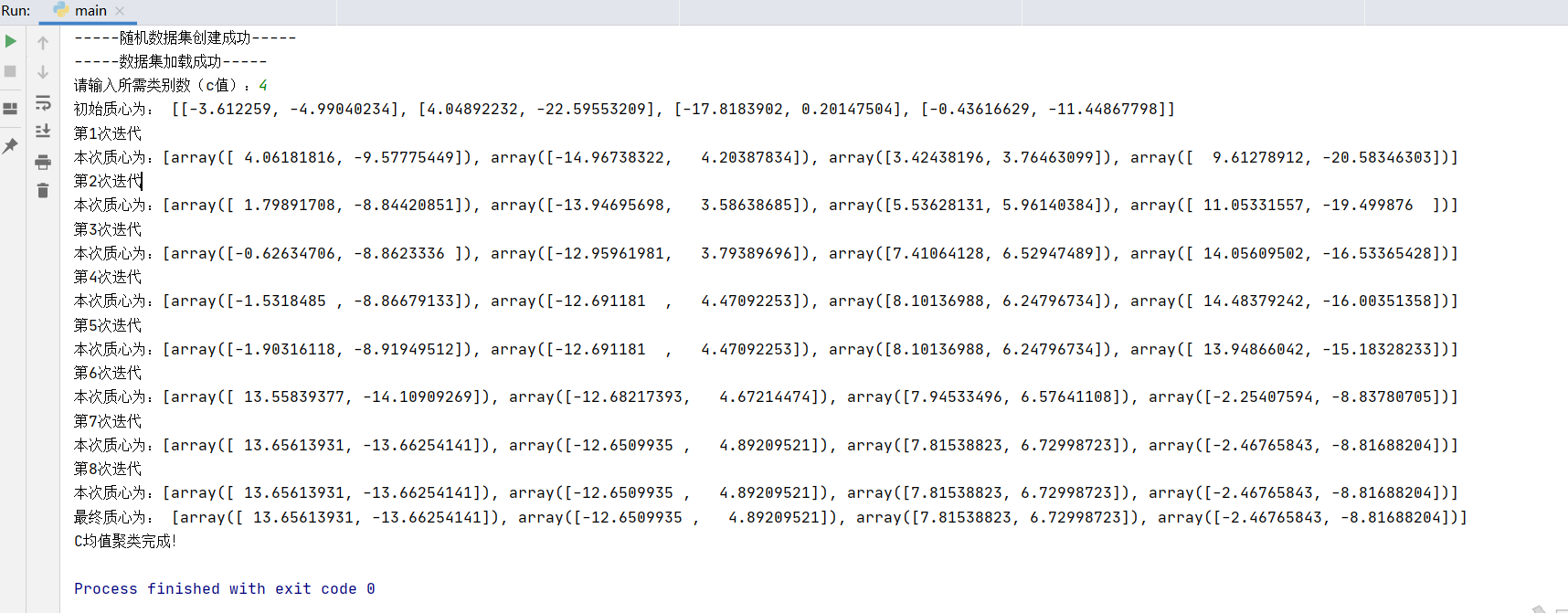
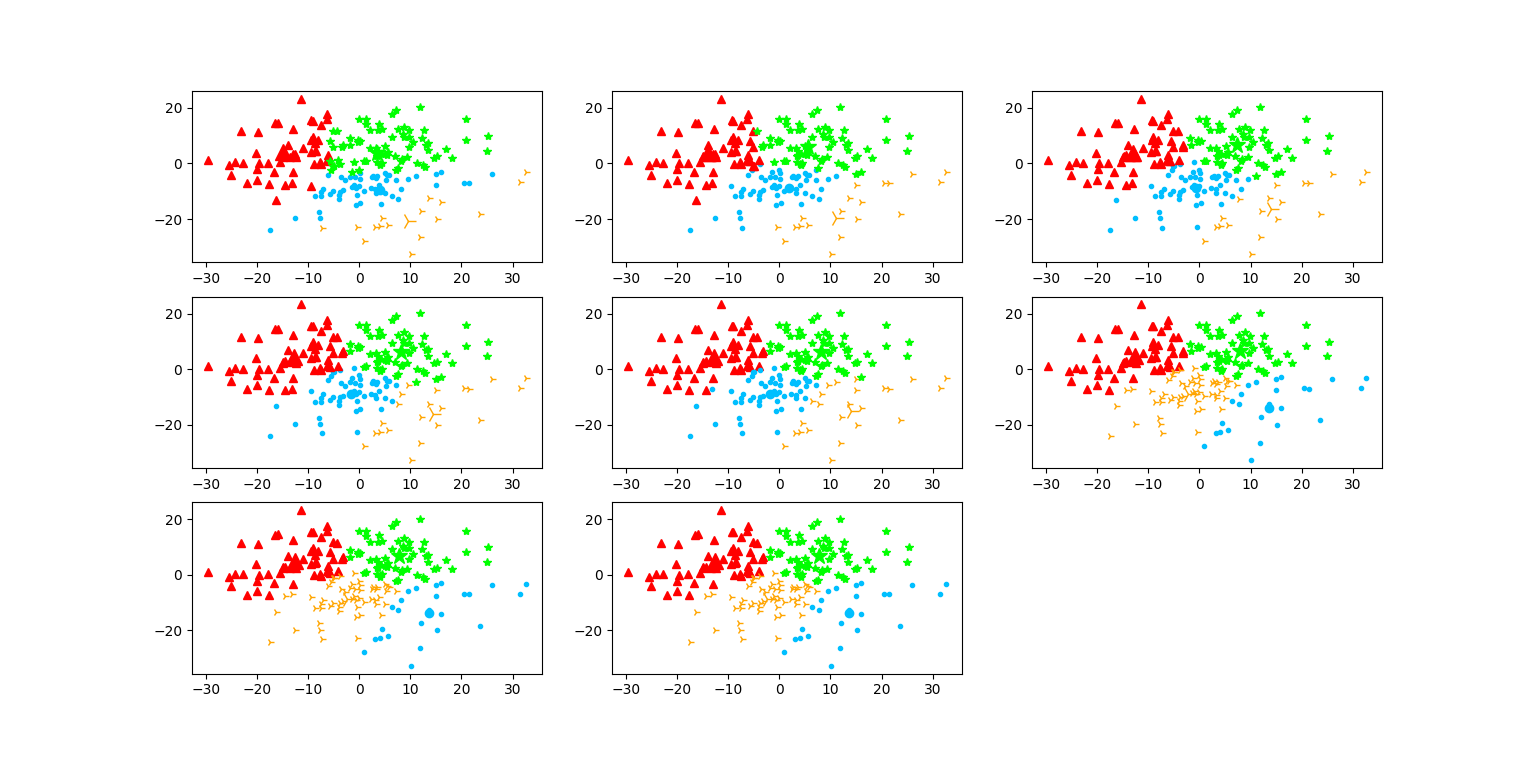
结果及分析

尝试了N加一次，因为用图片来显示聚类分析的结果还是很直观的，而且我感觉我设计的还蛮好看的哈哈哈哈哈。我对同一个数据集，用不同的类别数分别测试，相同的类别数多次测试，每一次的迭代次数都不尽相同；所以分类结果应该是依赖于分类中心的初始化的，如果说第一次产生的随机质点离最终的目标质点相差不大，那么迭代次数就小。
总结与反思

总结：

本次实验还是很成功的，算法不算难，学到了很多有自学过python，主要的方法和代码风格还比较了解，经过百度学习C-means算法，参考了部分资料后，很快就理解了，写起来也还行。自学python的时候是看书的，后面的实战部分都没有自己尝试，所以掌握其实也不好，这次还算是练了练手（python是真的很好用哈哈哈）

这次实验也让我更加理解了C-means算法的特点和实现方式。总结起来，C-means的优点有：①原理简单，实现容易，容易解释；②计算复杂度低，为O(Nmq)，其中N是数据总量，m是类别（即k），q是迭代次数；③聚类效果不错。缺点的话在本次实验中能够体现的就是①需要提前确定c值（提前确定多少类）；②分类结果依赖于分类中心的初始化。

反思：

因为确实对这块稀里糊涂的，查阅了很多资料，在看懂了csdn，博客园，微信公众号等等上的代码之后才慢慢摸索着写出来的，原理理解真的很重要，而且要多实战。经过自己的手打理解，对c均值聚类有了更深的理解，果然这一行，还是要多多实战。

posted @ 2021-01-15 00:28 littleegg 阅读(2200) 评论(0) 编辑收藏举报

刷新页面返回顶部

Littleegg

C均值聚类

C均值聚类

（一）实验目的

（二）实验条件

（三）算法基本思想

（四）算法流程图

（五）实验数据

（六）实验结果

公告