高分AT/CF乱做第二弹
date:2023.7~2023.8
再不学要退役了。暑期加练!!!
第一弹怎么感觉难度太高,题解含量有点大了/qd,这次多点分不是那么高的思维。
[CF1062F] Upgrading Cities/洛谷/CF
difficulty:2900
DAG 要先考虑拓扑排序!首先一个点被到达是好处理的,反向边再做一遍,累加能到达的点就好了。考虑拓扑排序的过程,一个点只有前驱都被遍历过才会被加入队列。记当前总共有 \(x\) 个点被加入过队列,\(i\) 可以到达/被到达的节点数量为 \(f_i\),那么当队列里只有一个节点的时候,它显然可以到达剩下的所有节点,所以 \(f_{top} += n - x\);当队列里有两个节点的时候,如果其中一个节点存在一个后继入度为 \(1\),即当前只能被这个节点到达,那么另一个节点肯定不符合条件,标记一下即可。最后判一下有多少个节点符合条件即可,需要注意的是按照上述方法并不会记录上能到达节点自身,故 \(f_i\) 需额外加上 \(2\)。submission
[CF542E] Playing on Graph/洛谷/CF
difficulty:2600
不同连通块之间显然没有影响,总答案是每个连通块的子答案和。注意到如果图中存在奇环,因为任选奇环中的两个点进行操作,会得到一个更小的奇环,所以存在奇环是有解的充要条件。充分性已经证明,接下来考虑必要性。不存在奇环的图即为二分图,二分图必定可以缩成一条链:以任意节点为根建立 bfs 树,则同深度节点间不存在连边,所以可以将同一深度的节点缩成一个点,于是得到一条链,必要性得证,同时也得到了构造方法。最后我们要使得这条链尽可能长,题目转化成求二分图的直径,判奇环用染色法即可,时间复杂度 \(\mathcal O(n^2)\)。submission
[CF1110G] Tree-Tac-Toe/洛谷/CF
difficulty:3100
牛牛分讨。首先 Bob 肯定赢不了,因为如果存在必胜策略,那么 Alice 作为先手拿过来用一定是赢得,所以接下来要做的是判断平局还是 Alice 赢。如果有一个点的度数 \(\geq 4\),显然 Alice 先手选这个点直接赢了。如果所有点的度数都 \(\leq 2\),那么就是一条链,结果一定是平局,Alice 下哪 Bob 在两边堵即可。如果有一个点的度数 \(= 3\),并且链接了 \(\geq\) 两个非叶子节点,那么第一轮选这个节点,第二轮选一个非叶子邻居节点就赢了,所以如果存在这种节点也是先手必胜的。剩下的只有三叉,后面延伸出一条长链;三叉,后面延伸出一条长链,又接了一个三叉这两种情况。前者随便手玩一下,显然为平局。
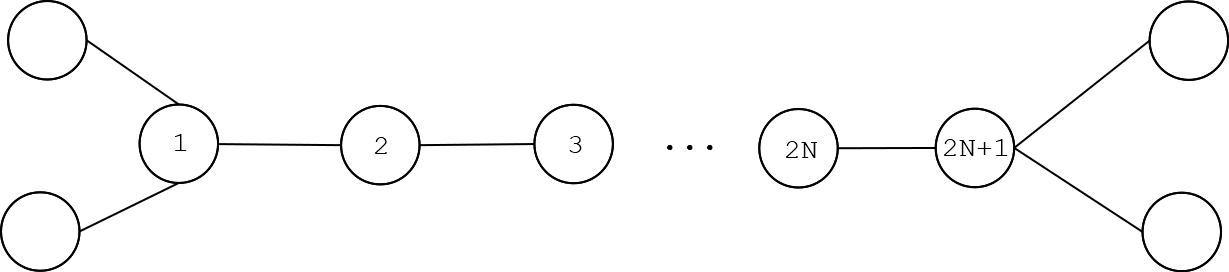
白色最开始染 \(2\) 号点,黑色如果染 \(3\) 号点白色直接染 \(1\) 号点,所以黑色必须染 \(1\) 号点。此时白色染 \(4\) 号点,黑色又只能染 \(3\) 号点 \(\cdots\) 如是白色染到 \(2N\) 号点,黑色染 \(2N − 1\) 号点之后,白色染 \(2N + 1\) 号点,那么最右边就会有两个未被染的点,白色就赢了。所以中间的链长度为奇数先手赢,否则平局。接下来的问题是如何处理开局已经是白色的点。
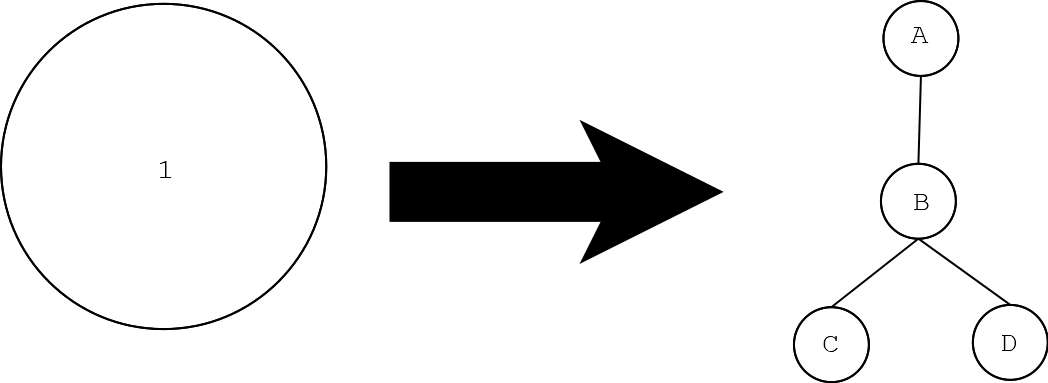
对于原图中的一个白点 \(1\),将其替换成右图的结构,并将原来与 \(1\) 相连的点与 \(A\) 相连。注意到如果一个人选择了 \(A\),那么下一轮对手必须选 \(B\),此时 \(CD\) 对对局胜负已没有影响,因为选他们是没有意义的。能够发现决策权又回到了第一个人,相当于第一个人白嫖到 \(A\) 为白色,所以是可以这样转化为等效结构的。先重新建图,然后跑上面的若干分讨 check 即可,复杂度 \(\mathcal O(n)\)。submission
[CF360E] Levko and Game/洛谷/CF
difficulty:2800
首先区间肯定是个幌子,每条边要么取到上界,要么取到下界。比较显然的贪心想法是钦定路线上的边都取下界,其他边都取上界,然后跑 dijkstra 判答案。但当另一条可能存在的最短路与钦定路线部分重合时这部分边是不好定值的。考虑跑两边 dijkstra,第一次尽量取得赢得局面,如果 \(s_1\) 和 \(s_2\) 到达一个点的最短路相等,那么就选权值为 \(r\),尽量让 \(s_1\) 出来的路径可能成为最短路;如果不能取得赢的局面,就再跑一遍尽量取得平局的局面,如果 \(s_1\) 和 \(s_2\) 到达一个点的最短路相等,那么就选权值为 \(l\),尽量让 \(s_2\) 出来的其他路径不成为最短路。时间复杂度 \(\mathcal O(m \log n)\)。submission
[CF1137C] Museums Tour/洛谷/CF
difficulty:2500
注意到 \(d\) 的范围,先拆点拆边,把每个城市拆成 \(d\) 个点,然后按照题意连边,然后再缩 SCC,一个 SCC 的权值为能到达的不同博物馆数量,需要拿桶判重,最后一号节点跑最长路即可。考虑为什么不会出现重复计算答案,这个问题出现当且仅当存在 \((u,d_1) \to (u,d_2)\) 且 \((u,d_1)\) 和 \((u,d_2)\) 属于两个 SCC,如果出现这种情况一定有 \((u,d_2) \to (u,d_1)\) (整循环节),所以与前面条件不符,故不会出现。时间复杂度 \(\mathcal O(nd)\)。卡常学到很多:内联函数不占用栈空间,访问边次数特别多推荐链表存图。submission
[ABC307Ex] Marquee/洛谷/AT
difficulty:2754
挺板的。FFT 做通配符匹配,循环的问题直接在主串前后补模式串长度 \(-1\) 个通配符即可。于是就 \(\mathcal O(T \log T)\),取 \(T = n + m\)。submission
[CF1779F] Xorcerer's Stones/洛谷/CF
difficulty:2500
性质题。注意到如果一个节点的子树大小为偶数,则一次操作将子树内的点变为同一个值,两次操作使子树内的点全部为零;大小为奇数,则一次操作将子树内的点变为同一个值,无论如何操作这个子树,每个点的值均不会改变。所以操作奇数子树大小的点是无用的。考虑做类似背包的可行性 DP,记 \(f_{i,j,k}\) 表示当前在点 \(i\),考虑了前 \(k\) 个子树,能否将 \(i\) 子树内所有点权变为 \(j\),边界即为 \(f_{i,val_i,0} = 1\),转移即为 \(f_{i,x \oplus y,k} |= f_{i,x,k - 1} \wedge f_{son_i,y,k}\)。考虑如何输出方案,令 DP 数组记录转移来的异或值,在 dfs 倒序枚举一遍所有儿子即可。特别的,给偶数子树大小的节点 \(f_{i,0,sonsiz_i}\) 打上特殊标记,若遍历到这种 DP 值,直接放入答案序列里。瓶颈在于树上背包的合并,做到 \(\mathcal O(n w^2)\),其中 \(w\) 为点权,有 \(w \leq 31\)。submission
[CF555E] Case of Computer Network/洛谷/CF
difficulty:2800
先缩边双,一个边双里的显然可以随便走。转化为树上问题,给定的限制是有向点对,这是好的。边转点后记两个标记:向上和向下,直接拆成 \(s \to lca \to t\) 后分别两端打不同标记,这个树上差分做就好了,最后遍历一遍看是否有边两种标记都有。注意图可能不连通的问题即可。submission
[CF1763F] Edge Queries/洛谷/CF
difficulty:3000
性质都没有什么用,缩点双建圆方树,如果一个点双大小为二那么这条边是用不上的,否则将方点权值设成其点双内部边的数量,于是答案即为圆方树路径上权值和。如何算一个点双内部有几条边呢?先存下来所有边建好圆方树,一遍 dfs 得出 father 和 depth,根据圆方树的性质,如果两个点深度相同并且父亲是同一个方点,那么其父亲便为他们共同所在的点双;或者是形如圆-方-圆,深度差二的两个圆点间有边,那么中间夹的那个方点即为共同所在的点双。直接 LCA + 差分求和即可做到 \(\mathcal O(n + q \log n)\)。submission
[CF1766F] MCF/洛谷/CF
difficulty:2800
有意思的题。这个数据范围感觉能直接流了,想想怎么流。要求容量和流量奇偶性相同,不妨先钦定奇数都流个 \(1\),这样每条边就都要求流偶数的流量。然后给容量都除以 \(2\),这样在新边上流一个相当于原来流两个,就满足偶数的要求了。因为不需要满足最大流,所以流的时候看一下当前增广出来的路费用为正就可以直接跳了。判无解的方法是除源点汇点外的点度数都为偶数;最后每个点的流出流入是相等的。submission
[CF1383C] String Transformation 2/洛谷/CF
difficulty:3100
对于每个 \(s_i\) 向 \(t_i\) 连边,得到若干个弱连通分量,单独做最后加起来即可。对于一个弱联通分量有 \(n\) 个点,它的解为 \(k\),那么该弱联通分量最大 DAG 至少为 \(2n - k - 1\)。考虑求解其 DAG 的过程,起初每个点单独属于一个 DAG,对于该联通分量中的一条边 \((u,v)\),如果 \(u,v\) 已经被合并在一个 DAG 中,那么删除掉 \(v\),DAG 的总大小减小 \(1\);否则合并 DAG,DAG 的数量会减小 \(1\),但是 DAG 的总大小不会改变。最后 DAG 的个数会变成 \(1\),因此需要 \(n - 1\) 条边来合并 DAG,于是剩下 \(n - k + 1\) 条边可以用来减小 DAG 大小,于是得到上述结论。因此 \(|DAG| \geq 2n - k - 1\),那么 \(k \geq 2n - |DAG| - 1\),于是问题转化成了求最大的导出子图为 DAG,考虑拓扑排序的过程,记录下每个点的出边集后,加入一个不在当前连通块中的点,需要满足这个点的出点不能在当前集合中,状压 DP 做到 \(\mathcal O(n 2^n)\)。submission


 浙公网安备 33010602011771号
浙公网安备 33010602011771号