题解:【CF1610I】 Mashtali vs AtCoder
从 \(k = 1\) 开始考虑,即为这道题。
记点 \(u\) 的 SG 函数为 \(f_u\),\(v\) 为点 \(u\) 的儿子,则有 \(f_u = \oplus (f_v + 1)\)。
首先每次操作是从根节点的一棵子树中选一条边删掉,这说明了根节点每个儿子的游戏是独立的,所以考虑使用 nim 和求解。假如说根节点有 \(k\) 个子树,那么将根拆成 \(k\) 个点,每个点下面连原先的一个儿子(即每个节点下面挂一个子树),根据 nim 和的结论,我们要求的答案即为 \(k\) 棵新树的 SG 函数异或起来。问题变成了在一棵树顶上新连出来一条边,该树的 SG 函数值会如何变化。
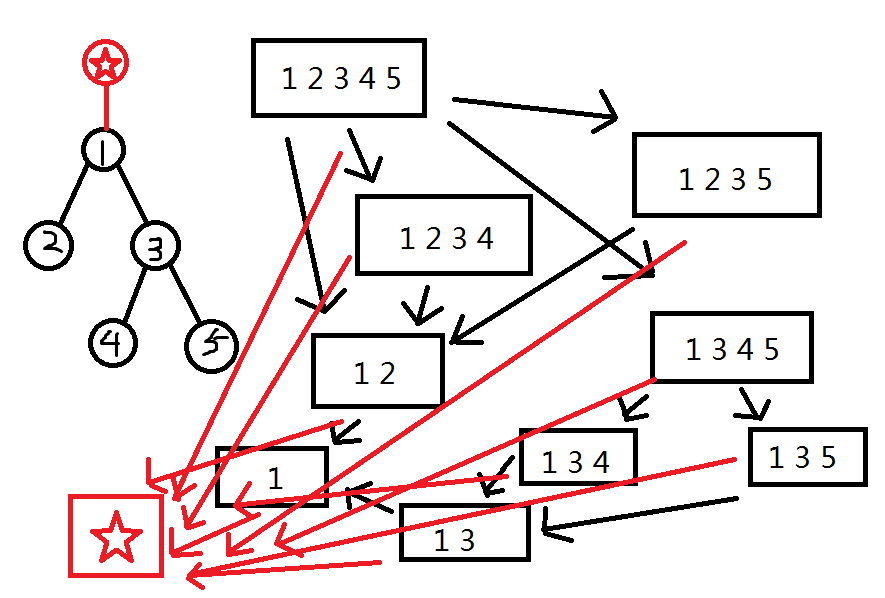
根据题目中任何时刻都可以选择当前局面中一条边 \((u,v)\) 切掉,画出博弈对应的有向图,发现这相当于给每一个节点都增加了一个后继的超级汇点,而且显然这个超级汇点为必败态,SG 函数为 \(0\)。原先图中 SG 函数为 \(1\) 的点变成了 \(2\),原来为 \(2\) 的点变成了 \(3\),以此类推,这个操作使得局面中所有状态的 SG 函数都偏移了 \(1\),于是可以归纳出上面的结论,一棵树的 SG 函数是所有子树的 SG 函数值 \(+1\) 的异或和。
接下来考虑加入更多的关键点,钦定依然以 \(1\) 号点为根,我们可以将整棵树划分成若干部分:
- 如果对于节点 \(u\),\(u\) 的子树内不存在关键点,但是对于它的父亲 \(v\),\(v\) 的子树内存在关键点。那么将 \(u\) 和其子树拉出来,再加上 \(v\) 点这是一个独立的游戏,答案为上面得到的结论:游戏的 SG 函数为这棵子树的 SG 函数值 \(+1\)。
- 刨除所有的第一种部分后,剩下的一坨东西满足度为 \(1\) 的点都是关键点。不妨将其看做无根树,接下来我们需要解决这棵树的 SG 函数。
这棵无根树的 SG 函数为树的边数 \(\mod 2\)。
首先有引理,对于存在这种关键点的树,\(\text{SG 函数} \equiv \text{树的边数} (\mod 2)\)。如果只删除一条边并不会导致删除,所以随便删掉一条边后剩下的两个子游戏的 SG 异或和 \(\not\equiv {边数} (\mod 2)\),据此这棵树 SG \(\leq \text{边数} \mod 2\)。对于边数为偶数的情况已经得解,至于边数为奇数的还不是特别理解,这里引用一下 ZJ 队长的证明:
任取一个度为 \(1\) 的节点和距其最近的度不为 \(2\) 的节点(对于度为 \(2\) 的节点,总有唯一的出边,因此该点唯一),并在两者的路径上去边。假设路径长度为 \(l\),将 \(l\) 分为 \(x\) 和 \(y\) 两段(其中 \(x + y = l − 1\)),这两段在新问题中都将作为第 \(1\) 种情况,而去掉后又是一个第 \(2\) 种情况,可以由归纳假设确定其 SG 值。
依然根据 nim 和,最后的答案就是各个部分的 SG 异或起来。具体可以如何实现呢?首先依然要做一遍以 \(1\) 为根的树形 DP,预处理出初始的每个点的 SG 函数以及父节点关系。考虑一次添加关键点 \(u\),有多少节点的贡献从第一种游戏变到了第二种游戏,显然为 \(u\) 的根链上之前不是第二种贡献的节点。记现在要修改节点 \(i\) 的贡献,根据异或的自反性,先异或上 \(SG_i + 1\) 消除贡献,然后再异或上 \(SG_i\) 作为新的贡献,最后处理加入到无根树中对无根树边数的变化,可以直接多异或一个 \(1\),综上式子就是 \(\oplus (SG_i + 1) \oplus SG_i \oplus 1\)。每次加入关键点可以直接暴力跳父亲,因为每个节点只会转变一次贡献,所以均摊下来时间复杂度是 \(\mathcal O(n)\) 的。
#include<bits/stdc++.h>
#define ld long double
#define ui unsigned int
#define ull unsigned long long
#define int long long
#define eb emplace_back
#define pb pop_back
#define ins insert
#define mp make_pair
#define pii pair<int,int>
#define fi first
#define se second
#define power(x) ((x)*(x))
#define gcd(x,y) (__gcd((x),(y)))
#define lcm(x,y) ((x)*(y)/gcd((x),(y)))
#define lg(x,y) (__lg((x),(y)))
using namespace std;
namespace FastIO
{
template<typename T=int> inline T read()
{
T s=0,w=1; char c=getchar();
while(!isdigit(c)) {if(c=='-') w=-1; c=getchar();}
while(isdigit(c)) s=(s<<1)+(s<<3)+(c^48),c=getchar();
return s*w;
}
template<typename T> inline void read(T &s)
{
s=0; int w=1; char c=getchar();
while(!isdigit(c)) {if(c=='-') w=-1; c=getchar();}
while(isdigit(c)) s=(s<<1)+(s<<3)+(c^48),c=getchar();
s=s*w;
}
template<typename T,typename... Args> inline void read(T &x,Args &...args)
{
read(x),read(args...);
}
template<typename T> inline void write(T x,char ch)
{
if(x<0) x=-x,putchar('-');
static char stk[25]; int top=0;
do {stk[top++]=x%10+'0',x/=10;} while(x);
while(top) putchar(stk[--top]);
putchar(ch);
return;
}
}
using namespace FastIO;
namespace MTool
{
template<typename T> inline void Swp(T &a,T &b) {T t=a;a=b;b=t;}
template<typename T> inline void cmax(T &a,T b) {a=a>b?a:b;}
template<typename T> inline void cmin(T &a,T b) {a=a<b?a:b;}
struct ModTool
{
#define TA template<typename T,typename... Args>
#define TT template<typename T>
int Mod;
ModTool(int MOD=998244353):Mod(MOD){}
void ChangeMod(int MOD) {Mod=MOD;}
TT inline void Madd(T &a,T b) {a=a+b>Mod?a+b-Mod:a+b;}
TT inline void Mdel(T &a,T b) {a=a-b<0?a-b+Mod:a-b;}
TT inline void Mmul(T &a,T b) {a=a*b%Mod;}
TT inline void Mmod(T a) {a=(a%Mod+Mod)%Mod;}
TT inline T Cadd(T a,T b) {return a+b>=Mod?a+b-Mod:a+b;}
TT inline T Cdel(T a,T b) {return a-b<0?a-b+Mod:a-b;}
TT inline T Cmul(T a,T b) {return a*b%Mod;}
TT inline T Cmod(T a) {return (a%Mod+Mod)%Mod;}
TA inline void Madd(T &a,T b,Args... args) {Madd(a,Cadd(b,args...));}
TA inline void Mdel(T &a,T b,Args... args) {Mdel(a,Cadd(b,args...));}
TA inline void Mmul(T &a,T b,Args... args) {Mmul(a,Cmul(b,args...));}
TA inline T Cadd(T a,T b,Args... args) {return Cadd(Cadd(a,b),args...);}
TA inline T Cdel(T a,T b,Args... args) {return Cdel(Cdel(a,b),args...);}
TA inline T Cmul(T a,T b,Args... args) {return Cmul(Cmul(a,b),args...);}
TT inline T qpow(T a,T b) {int res=1; while(b) {if(b&1) Mmul(res,a); Mmul(a,a); b>>=1;} return res;}
TT inline T qmul(T a,T b) {int res=0; while(b) {if(b&1) Madd(res,a); Madd(a,a); b>>=1;} return res;}
TT inline T spow(T a,T b) {int res=1; while(b) {if(b&1) res=qmul(res,a); a=qmul(a,a); b>>=1;} return res;}
private:TT inline void exgcd(T A,T B,T &X,T &Y) {if(!B) return X=1,Y=0,void(); exgcd(B,A%B,Y,X),Y-=X*(A/B);}
public:TT inline T Ginv(T x) {T A=0,B=0; exgcd(x,Mod,A,B); return Cmod(A);}
#undef TT
#undef TA
};
}
using namespace MTool;
inline void file()
{
freopen(".in","r",stdin);
freopen(".out","w",stdout);
return;
}
bool Mbe;
namespace LgxTpre
{
static const int MAX=300010;
static const int inf=2147483647;
static const int INF=4557430888798830399;
static const int mod=1e9+7;
static const int bas=131;
int n,x,y,tmp;
vector<int> G[MAX];
int sg[MAX],fa[MAX],vis[MAX];
void dfs(int now,int father)
{
fa[now]=father;
for(auto to:G[now]) if(to!=father) dfs(to,now),sg[now]^=sg[to]+1;
}
inline void lmy_forever()
{
read(n);
for(int i=1;i<n;++i) read(x,y),G[x].eb(y),G[y].eb(x);
dfs(1,0),tmp=sg[1],putchar(tmp?'1':'2');
for(int i=2;i<=n;++i)
{
for(int now=i;now!=1&&!vis[now];now=fa[now]) vis[now]=1,tmp^=sg[now]^(sg[now]+1)^1;
putchar(tmp?'1':'2');
}
puts("");
return;
}
}
bool Med;
signed main()
{
// file();
fprintf(stderr,"%.3lf MB\n",abs(&Med-&Mbe)/1048576.0);
int Tbe=clock();
LgxTpre::lmy_forever();
int Ted=clock();
cerr<<1e3*(Ted-Tbe)/CLOCKS_PER_SEC<<" ms\n";
return (0-0);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号