浅谈一类优化思想:费用提前计算
写在前面
这个知识点虽然微乎其微,但却十分有用。网上貌似没有什么人愿意整理这项内容,于是便随意记录了一下,如有不足还请指出。
不得不说我太弱了,感觉现在网上很多题解报告都很抽象模糊。所以这篇文章也主打的就是一个感性理解,可能显得讲的略有琐碎。有问题欢迎提出。
配套使用题单,除了例题外还有一些能用到这个知识点的题,但仍数量不多,欢迎私信扩容。
当前决策对未来行动的费用影响只与当前决策有关
不如从一道经典的例题入手:
有 \(n\) 个任务按顺序分批执行,每批任务开始需要一个固定的启动时间 \(S\)。第 \(i\) 个任务花费的时间是 \(t_i\),每个任务的花费是它完成的时刻乘上它自身的费用系数 \(f_i\)。需要找到一个最佳的分批顺序使得总费用最小。
这里不考虑高端的斜率优化,看看暴力的 DP 是怎么优化的。首先有一个显然的 \(\mathcal O(n^3)\) 的式子。记 \(T_i = \sum_{j=1}^i t_j\),\(F_i = \sum_{j=1}^i f_j\),设 \(g_{i,j}\) 表示将前 \(i\) 个任务分成 \(j\) 个组的最小花费,有转移方程:
注意到这个 DP 的状态设计之所以记录 \(j\) 这一维,是因为需要知道前面有多少次启动了机器,即分成了多少批任务。但是事实上并不关心启动了几次机器,只关心到底因为 \(S\) 造成了多少费用。一批任务启动的时间 \(S\) 会累加到后面每一个任务上,所以可以将对后面任务造成的影响,累加到当前的费用中。设 \(g_i\) 表示把前 \(i\) 个任务分成若干个组的最小花费,有转移方程:
这样成功将问题优化到了 \(\mathcal O(n^2)\)。
可以发现在这个问题中,选择一个决策会带来一个对未来的代价,但又不能通过在状态中再增加一维记录代价满足需求。这个代价是必然的,无论后面如何选择,都不会改变这个决策所带来的影响,这就是当前决策对未来行动的费用影响只与当前决策有关,我们可以把这个代价看作决策本身的费用,将未来的代价提前计算出来,在决策的时候就计算上它将会带来的代价,通过状态向后传递。
这类思想很经典的应用是以关路灯为母题的一类区间 DP,不妨以其为例题来探索一下。
在一条线段上有 \(n\) 个路灯分别在 \(p_i\) 的位置上,每个单位时间造成 \(c_i\) 的代价。一个人起初在 \(S\),每个单位时间可以移动一个单位距离,走到路灯的位置可以关掉路灯,使其停止造成代价。求关掉所有路灯造成的最小代价。
如果不知道有费用提前计算这么个东西,那么设计的状态可能是 \(f_{i,j,tim,0/1}\) 表示关掉了 \([i,j]\) 这个区间的灯,已经进行了 \(tim\) 的时间,现在在左/右端点的最小花费。转移则为关掉上一个路灯的花费,加上总共用过的时间乘当前选的路灯的功率,这样设计复杂度必然爆炸。
但是我们现在会了新东西。 类似上一道题,我们发现之所以要记录 \(tim\) 这一维度,是因为要知道现在关掉的灯运行了多久,也就是曾经的决策影响现在的代价。事实上一个路灯只要在一个时刻没有被关掉,它就会不断产生代价,因此可以在决策选择哪一个路灯时,将所有开着的路灯造成的代价作为关掉它的费用一块计算出来,提前累加在这个状态中。这样便成功压缩掉了一维,记 \(f_{i,j,0/1}\) 表示已经关掉了 \([i,j]\) 区间的路灯,现在在左/右端点的最小花费。得到了转移方程:
距离与功率和可以使用前缀和什么的优化,这里不多赘述。
这一类问题还包括但不限于[SDOI2008] Sue 的小球,修缮长城 Fixing the Great Wall和[BalticOI 2009 Day1] 甲虫,思想和做法都是相同类似的。
做完了经典的模型,再来些不一样的题看看吧。
给出一个数 \(x\),对其进行 \(m\) 次操作,分别为 \(p\%\) 的概率对它 \(\times 2\),\((100-p)\%\) 的概率对它 \(+1\)。求该数最终二进制下末尾 \(0\) 的个数的期望。
这两个操作分别对应着二进制下在末尾插入一个 \(0\),将末尾一串 \(1\) 变成 \(0\) 再将最后一个 \(0\) 变成 \(1\)。这个 \(+1\) 操作造成的进位十分棘手,怎么样才能尽量减小它的影响呢?考虑时空倒流,从后往前操作。注意到一旦出现了一个 \(\times 2\),那么在时间轴上往前的一个 \(+1\) 操作将变成 \(+2\),不会再对最低位造成影响。
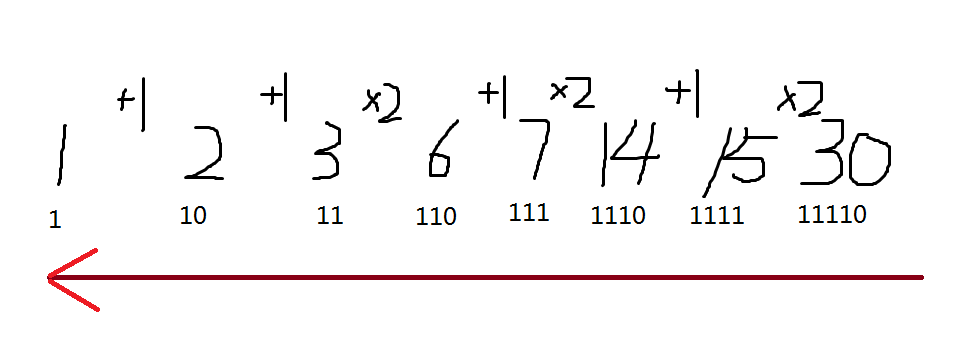
上图的 \(2 \to 6 \to 14 \to 30\) 的最低位的 \(0\) 一直没有受到影响。那么设 \(f_{i,j,k}\) 表示进行了末尾的 \(i\) 次操作,最后连着进行了 \(k\) 次 \(\times 2\) 的操作(即通过 \(\times 2\) 在末尾获得了 \(k\) 个 \(0\)),在这 \(k\) 个 \(0\) 之前造成了 \(+j\) 的影响。可以发现进行了 \(\times 2\) 操作,如果当前的 \(j\) 为偶数,则可以看做进行了 \(j / 2\) 次 \(+1\),末尾多进行了一个 \(\times 2\)(即多获得了一个 \(0\));如果当前的 \(j\) 为奇数,则相当于 \(k\) 个 \(0\) 前面的第一个数是 \(1\),无论怎么操作后面 \(0\) 的数量都将不再变化,可以直接计算贡献。所有操作进行完之后,可以将初始值看做先进行了 \(x\) 次 \(+1\),再把这部分贡献算上。
这样就得到了一个 \(\mathcal O(m^3)\) 的做法。能不能继续优化呢?回顾前面讲的两道题的答案计算式子,对于任务安排,答案是 \(Cost(\text{花费}) = Time(\text{时间}) \times f(\text{费用系数})\);对于关路灯,答案是 \(W(\text{功}) = P(\text{功率}) \times T(\text{时间})\)。没错,正是因为他们的计算为一次函数,具有线性性,所以可以提前计算,直接累计(不是一次函数的状况读者可以思考一下为什么不行,后文还会阐述)。不要忘记了,期望本身也具有线性性!所以在 \(\times 2\) 且 \(j\) 为偶数的时候,我们把通过 \(\times 2\) 多获得的那一个 \(0\) 单独计算出来,权值为 \(1\),直接乘上概率累加到答案中即可。这样便可以省掉 \(k\) 这一维,记 \(f_{i,j}\) 为进行了末尾 \(i\) 次操作,使得若干个 \(0\) 之前有 \(+j\) 的影响。记一个数 \(i\) 末尾 \(0\) 的个数为 \(sum_i\),答案就是 \(\sum_{i=0}^{k-1} \sum_{j=0|j \% 2 = 0}^i f_{i,j} \times p + \sum_{i=0}^k f_{k,i} \times sum_{x+i}\)。
参考代码:
cin>>x>>k>>p,p/=100,f[0][0]=1.0;
for(int i=0;i<k;++i) for(int j=0;j<=i;++j) if(f[i][j])
{
if(!(j&1)) f[i+1][j/2]+=f[i][j]*p,ans+=f[i][j]*p*1ll; //这里为了方便理解,因为权值为1
f[i+1][j+1]+=f[i][j]*(1-p);
}
for(int i=0;i<=k;++i) ans+=__build_ctz(x+i)*f[k][i];
cout<<fixed<<setprecision(9)<<ans<<'\n';
给定一个长度为 \(n\) 序列 \(A\),有 \(\forall A_i \in [1,k]\)。每次操作可以交换两个相邻的元素,求最少操作多少次可以使得 \(A\) 中存在一个区间为 \(\exists p,A_p = 1,A_{p+1} = 2,\cdots,A_{p+k-1} = k\)。
注意到这个 \(k\) 特别小,可以考虑一下状压 DP。设 \(f_{i,S}\) 表示当前考虑到了序列的前 \(i\) 个数,最终答案中已经排好了 \(S\) 二进制位上为 \(1\) 的数并连在了一起。当决策一个新的数的时候,可以选择放入最终答案,也可以选择不放入最终答案。不妨先假设新插入的这个数已经紧贴在先前排好的序列右边了,要插入的话直接按照规则插入,不需要计算从别的地方移动过来的费用。如果选择放进最终答案,费用就是把他移动到相应的位置,即以其为结尾的序列的逆序对的个数;如果不选择放进最终答案,那么代价就是让最后答案中所有比它小的数或所有比它大的数“跨过它”,但是每个数具体被跨过了几次,我们并不好知道。考虑费用提前计算,把“被跨过了几次”转换成“有多少个数跨过了它”,将费用均摊在每个剩下选中的每个点上。那么就是所有比他小的数都要跨过它一次,或者所有比它大的数都要跨过它一次,两者贪心取 \(\min\) 即可。这时注意到一个 \(f_i\) 的决策只与 \(f_{i-1}\) 有关,于是又节省掉一维,时间复杂度 \(\mathcal O(n \times 2^k)\)。
参考代码:
#define all ((1<<k)-1)
cin>>n>>k,memset(f,0x3f,sizeof f),f[0]=0;
for(int i=1;i<=n;++i)
{
cin>>x,--x;
for(int j=all;~j;--j) if(f[j]!=INF)
{
if(!(j>>x&1)) f[j|(1<<x)]=min(f[j|(1<<x)],f[j]+__builtin_popcount(j&(~((1<<x)-1))));
f[j]+=min(__buildtin_popcount(j),__builtin_popcount(j^all));
}
}
cout<<f[all]<<'\n';
现在再来系统总结一下使用这类优化方法的情景:
- 无论以后发生什么,当前对未来的代价都不会被改变,可以将对未来的代价当做当前决策本身的费用提前计算。
- 对状态增加一维来记录决策对未来的影响造成的复杂度代价过高,不能接受,考虑直接在当前代价中提前计算。
- 时间观即从过去考虑当前。
- 对未来的代价是线性的关系,根据线性性可以直接累加。
对于第四点,我们将在后文讨论不是线性的另一种状况。
当前决策对未来的贡献与未来有关
依然通过一道例题来引入:
给一个长度为 \(n\) 的方块序列,每个方块有一个颜色,每次消除一段颜色相同长度为 \(x\) 的方块,并获得 \(x^2\) 的分数,消除后剩下的方块会合并起来。寻找一种最优的消除方式使得最终得分尽可能大,求最大的得分。
依然是序列上的操作,考虑使用使用区间 DP 来解决。首先把颜色相同段缩成一个点,记录颜色和长度。套路的,设 \(f_{i,j}\) 表示消除了 \([i,j]\) 获得的最大得分,那么对于除去合并的消除转移方程也是十分的好写 \(f_{i,j} = \max(f_{i+1,j} + len_i^2,f_{i,j-1} + len_j^2)\)。那么怎么跨区间合并呢?如果保存状态记录当前决策每一段方块是否被消除,依旧是奇大无比的神秘复杂度,无法承受。类比关路灯的“费用提前计算”,我们预先计算得分,考虑当前消掉了一个长度为 \(\mathcal L\) 的方块,之前剩下了一个长度为 \(\mathcal T\) 的方块,但是他们并不能简单的合并,因为现在的得分函数是二次函数而非线性关系,\(\mathcal L^2 + \mathcal T^2 \neq (\mathcal L + \mathcal T)^2\),也就是过去的贡献和现在消去的长度是相关的,将时态向后整体推一个,便引出了我们的主题:当前决策对未来的贡献与未来有关。
既然不能从过去考虑现在,那能不能从现在考虑未来呢?如果在当前决策把未来可能出现的情况提前计算好,通过状态传递到了未来,那到了未来是不是能直接把这个决策拿来用,是不是就能够进行转移了呢?不妨设 \(f_{i,j,k}\) 表示消掉了 \([i,j]\) 这个区间,且后面有 \(k\) 个位置和 \(j\) 位置合并在一起消掉了。对于这个题,考虑为什么只需要记录 \(j\) 右边有多少个和它一起消掉了呢?这里引用一下论文里的证明:
假设现在有四个位置 \(i < j < k_1 < k_2\) 且处理好了 \([i,j]\),记“关系”的含义为两个位置未来会连在一起被消掉。假如说有关系 \(i \to k_1\) 和 \(j \to k_2\),那也就是说 \([j + 1,k_2 - 1]\) 间的块要在 \(j\) 被消掉前消掉,所以 \(j\) 之前的所有点不能往这个区域内连关系。因此得到了 \([i,j - 1]\) 内的块只能往 \([i,j]\) 上面连关系,而只有 \(j\) 自己能往 \(j\) 往后的区域连。
有了这个关系,方程便十分的好写了。如果 \(j\) 和后面 \(k\) 个块一起消掉,就有 \(f_{i,j,k} = f_{i,j-1,0} + (k+1)^2\);如果在 \([i,j-1]\) 这个区间中还有和 \(j\) 颜色相同的块 \(x\),那么可以先消除 \([x+1,j-1]\),然后再合并 \(x\) 和 \(j\) 一起消除,于是有 \(f_{i,j,k} = f_{i,x,k+1} + f_{x+1,j-1,0}\)。最后的答案即为 \(f_{1,n,0}\)。需要枚举端点 \(i,j\),以及右边合并个数 \(k\),还有在考虑区间 \([i,j]\) 的时候对于第二个决策枚举左边的断点 \(x\),因此时间复杂度 \(\mathcal O(n^4)\)。
回顾这个问题,我们起初想使用费用提前计算,把每次对未来的贡献摊在当前自己身上。可是发现未来的决策并不只于当前决策有关,还与未来本身状态相关。于是又开了一维状态,将目光放长远,预测未来可能出现的状况并计算,记录在状态中传递到未来,并在未来直接使用,这依然是一类费用提前计算的问题。
如同上一门类一样,这类问题很经典的应用是以[IOI2005]Riv 河流为母题的一类树形 DP,不妨以其为例题来探索一下。
给定一棵 \(n\) 个点的树,点边均带权。你可以选取 \(k\) 个关键点(根节点本身为关键点且不计算在 \(k\) 个之内),使得每个节点到离他最近的是关键点的祖先(记为 \(F_i\))的权值和最小,权值和的定义为 \(\sum_{i}^{n} dis_{i \to F_i} \times val_i\)。
不失一般性的,可以设 \(f_{i,j,0/1}\) 表示现在在 \(i\) 号节点,在 \(i\) 和 \(i\) 的子树中选取了 \(j\) 个关键点,有没有选取 \(i\) 的最小权值和。但是这样有一个巨大的问题——我们并不容易知道具体有多少个节点选择了 \(i\) 为祖先关键点,无法统计答案。既然不知道有多少个节点选择了 \(i\) 为祖先关键点,那我们不妨反着考虑:能不能很方便的知道当前节点选择了谁作为祖先关键点呢?如果知道了这个,那只需要把 \(i\) 上的答案再合并到 \(F_i\) 上就好了。
考虑 我们刚刚学会 的“当前决策对未来的贡献与未来有关”,这个句子和我们想搞的“当前节点对祖先的贡献与祖先有关”简直就是排比句啊!我们可以预测选择的节点是谁,并把它记录在状态中,于是就得到了设 \(f_{i,j,k,0/1}\) 表示现在在 \(i\) 号节点,在 \(i\) 和 \(i\) 的子树中选取了 \(j\) 个关键点,其中 \(i\) 的祖先关键点为 \(k\),有没有选取 \(i\) 的最小权值和。首先遍历整棵树,在每个节点上先枚举它的祖先关键点是谁,再枚举在它和它的子树中选了几个关键点,对于每个不同数量的关键点的决策做一个类似于树上背包的东西,即对于每一个子节点枚举在它和其子树中共选择了 \(1 \sim k\) 个关键点,综上我们得到了一个时间复杂度为 \(\mathcal O(n^2k^2)\) 的 优秀 算法。
这种树形 DP 将本应在当前节点计算的费用延后到它的子孙上,预测并记录子孙的状态,类似的题目也是层出不穷,例如[NOI2006] 网络收费和[NOI2008] 奥运物流。
因为笔者见识较少,所以对于第二种问题遇到的并没有第一种那么多,因此也没有准备更多的例题。
我们不如趁此再来总结一下使用这类优化方法的情景:
- 未来的费用并不只于当前代价相关,还与未来本身的状态相关。
- 通过增加一维状态来记录对未来的预测,从而在未来能够直接使用。
- 时间观从当前考虑未来。
- 对未来的代价并非线性的关系,不能简单的累加。
一点小小的扩展
在上文中,我们通过改变时间观,用“费用提前计算”这种特殊的方法有效的优化了许多 DP 式子。事实上有关费用提前计算的一些技巧不止适用于 DP 的优化,我们以一个例子大概了解一下:
有 \(n\) 个车主来修车,总共有 \(m\) 个维修技术人员,不同技术人员对不同的车维修时间不同,现在需要安排维修顺序使得顾客平均等待时间最少。求最小平均等待时间。
平均等待时间最少,就是总等待时间最少。类似于提前计算中的第二个题,一个人到底等了多长时间并不好计算,但是一个人到底被等了多长时间是好知道的,所以通过费用提前计算,把一个人等的时间摊到每个对其来说需要被等的人身上。我们将维修人员拆点,连边表示第 \(i\) 个车主的车由第 \(j\) 个维修人员修,且是这个维修人员修的倒数第 \(k\) 辆车,那么费用即为 \(k \times tim_{i,j}\),因为倒数第 \(k\) 个维修,算上其自己会共有 \(k\) 个人等待。那么剩下的就是费用流板子了。
套路是死的,但是人的脑子是活的;问题是做不完的,但是思想是在总结经验和大胆猜想中不断提升的。只要我们敢于探索,勇于尝试,总有一天能够实现身为 OIer 的梦想。
参考资料与致谢
- 徐源盛 《对一类动态规划问题的研究》
- 部分题解与题目来自 do_while_true 的汇总和指导
- 感谢 Larry76 和 My_Youth 的阅读意见反馈



 浙公网安备 33010602011771号
浙公网安备 33010602011771号