题解：【ABC292F】 Regular Triangle Inside a Rectangle
不妨设 \(a \le b\)。显然当三角形三个点都在矩形边上的时候可以得到答案。
通过手玩我们可以发现，当正方形推广到矩形的过程中，我们将一边拉长，三角形就可以不断往下放来增长。直到达到一个临界值三角形一边和矩形一边重合，此时限制在于短边。不难得出这个临界值为 \(b = \frac{2 \sqrt{3}}{3} a\)。
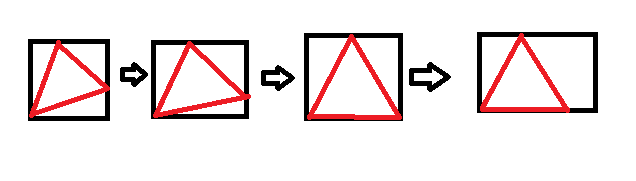
定义三角形和 \(a\) 边的夹角为 \(\theta\)，三角形边长为 \(l\)，由上可以得出：
\[\theta
\begin{cases}
= 15^{\circ} \; (a = b) \\
\in (15^{\circ},30^{\circ}) \; (a < b < \frac{2 \sqrt{3}}{3} a) \\
= 30^{\circ} \; (a = \frac{2 \sqrt{3}}{3}) \\
\end{cases}
\]
当 \(b \in (a,\frac{2 \sqrt{3}}{3} a)\) 时，我们可以得到方程：
\[\frac{b}{\cos{30^{\circ} - \theta}} = \frac{a}{\cos{\theta}}
\]
易得出 \(\frac{b}{a} = \frac{\sqrt{3}}{2} + \frac{1}{2} \tan{\theta}\)。
从而有 \(\tan{\theta} = \frac{2b}{a} - \sqrt{3}\)。
进而得出 \(\frac{1}{\cos^2{\theta}} = \tan^2{\theta} + 1 = \frac{4b^2}{a^2} - \frac{4 \sqrt{3} b}{a} + 4\)。
由 \(l^2 = \frac{a^2}{cos^2{\theta}}\) 得到 \(l\)。
综上：
\[l =
\begin{cases}
2 \sqrt{b^2 - \sqrt{3}ab + a^2} \; (a \le b \le \frac{2 \sqrt{3}}{3} a) \\
\frac{2 \sqrt{3}}{3} a \; (b > \frac{2 \sqrt{3}}{3} a) \\
\end{cases}
\]
