题解：【SWTR-8】15B03
前言
本篇题解大量配图！
作为一道非常好的有思维深度的题，必须写篇题解记录一下。
谨以此篇献给我的第一道构造题。
第一问（80 pts）
求需要撤去多少张桌子。
将问题转化成最多能放多少张桌子，然后用总数减去即可。
由于两张桌子不相邻需要保证对于 $ \forall (i,j) $ 满足 $ \vert i-i' \vert \le 1$ 且 $ \vert j-j' \vert \le 1$，所以当我们摆下一张桌子，下一张桌子一定跟这张桌子隔了一行或者一列。
当行（列）为偶数时，可以发现摆放的时候桌子的数量和比它少一行（列）的情况是相等的，为了计算方便可以直接去掉那一行（列），然后再下一问的时候加回来即可。
因此我们可以得出公式：
\(Code\)
bool p=1,q=1;
cin>>n>>m;
r=n*m;
if(n%2==0) n--,p=0;
if(m%2==0) m--,q=0;
r-=(n/2+1)*(m/2+1);
cout<<r<<" ";
第二问（20 pts）
性质一 （？ pts）
这个性质虽然没有 sub 单独列出来，但是在测试点里面存在。
考虑只有一张桌子的情况，显然这时距离应该为 \(0\)。
\(Code\)
if(n*m-r==1) {cout<<"0.000000000"<<endl; continue;}
性质二 n=1 （4 pts）
依然分奇偶讨论。
当 m 为奇数时，观察下图：
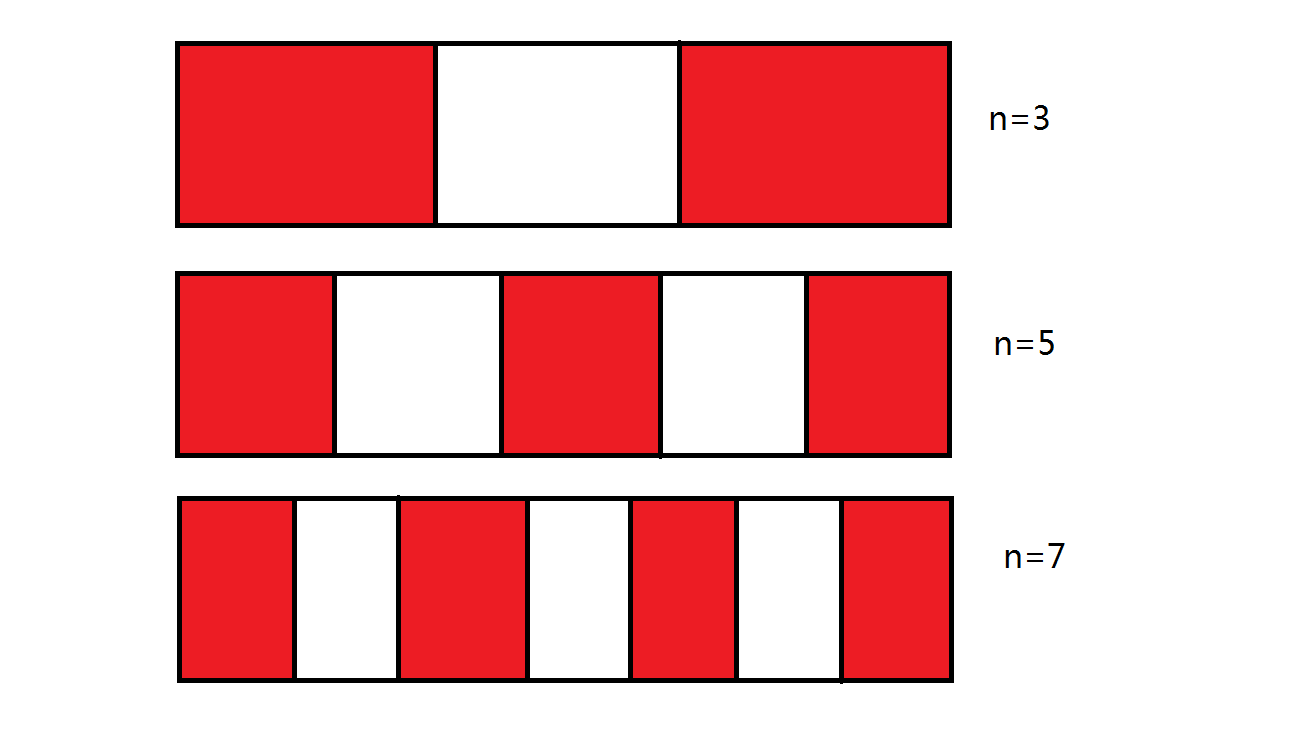
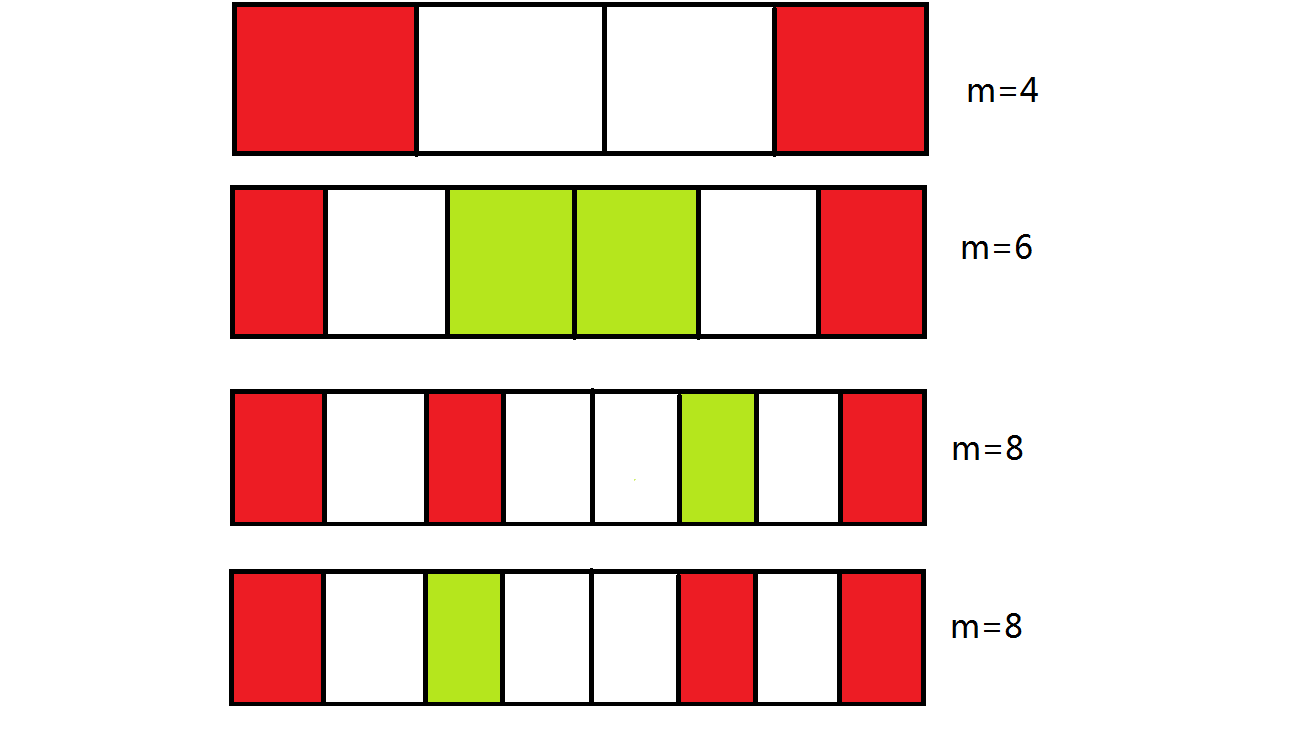
可以发现，当摆放的桌子为偶数个时，我们将他们对半分开，左半部分的到最右一个端点为最远距离，右半部分的到最左一个端点为最远距离；而且可以发现，对称的两张桌子到最远端点的距离都相等。当摆放的桌子为奇数个时，最中间的这张桌子到两端距离自然相等，在多算上即可。
当 m 为偶数时，观察下图：
绿色表示放在这两个地方都可以。
可以发现，无论摆放的桌子是奇数个还是偶数个，它们的摆放距离规律都跟奇数个类似。只不过当桌子越过中间的对称轴时，我们需要先再跳一个格子，然后再隔一个摆一张。
因此我们可以将这个长条折半，只算一半的距离最后乘二即可。
\(Code\)
//q是上面判断m奇偶性的
if(n==1&&(q))
{
for(int i=0;i<(m+1)/2/2;i++)
ans+=(m-2*i);
ans*=2;
if((m/2)%2==0) ans=ans+m-(m-1)/2;
cout<<fixed<<setprecision(9)<<ans<<endl;
}
else if(n==1&&(!q))
{
for(int i=0;i<=m/4;i++)
ans+=(m-2*i);
ans*=2;
if((m/2)%2==1) ans=ans+(m+2)/2;
cout<<fixed<<setprecision(9)<<ans<<endl;
}
性质三 n 和 m 都是奇数 （3 pts）
可以发现，这个性质把 n 从 1 延伸到了更多行，上一个性质中是 m 为偶数的情况较难处理，而这个性质简单在 m 只会是奇数。
我们在上个性质中发现了行为 1 时列的性质，那行会不会具有同样的性质呢？
观察下图：
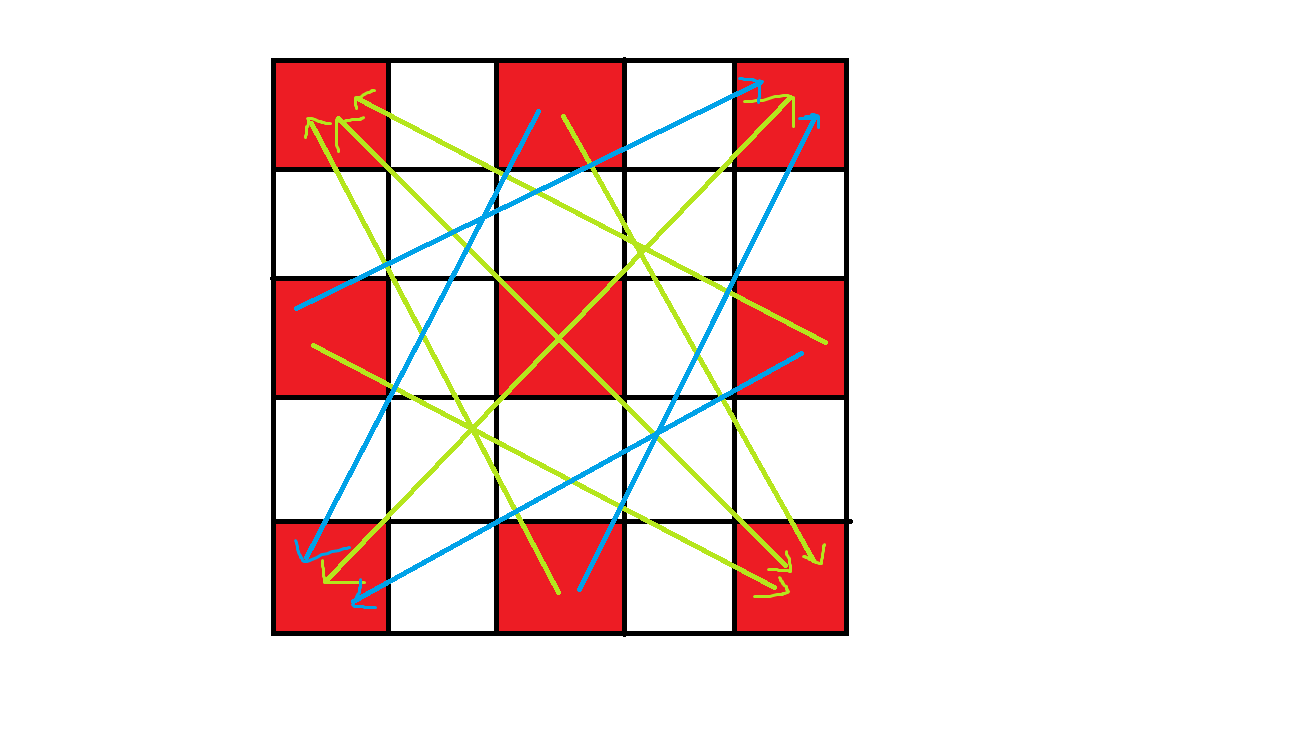
蓝色的箭头是选这个距离也可以，是一样长的。
推荐再配合题目样例一中的图共同食用。
可以发现对于任意一张桌子，它们的最远距离是到和它们相对的角上去。
无独有偶，无论行还是列，关于行、列中线对称的桌子最远距离都是相等的。比如上图中，从行来看，\((1,1)\) 和 \((5,1)\)，\((1,3)\) 和 \((5,3)\)，\((1,5)\) 和 \((5,5)\) 是对称的；从列来看，\((1,1)\) 和 \((1,5)\)，\((3,1)\) 和 \((3,5)\)，\((5,1)\) 和 \((5,5)\) 是对称的。
因此我们可以把这个方形分成四等份，只算其中一份就行。
无特殊性质 （20 pts）
既然找到了行列都为奇数的规律，不妨大胆猜想，偶数的时候行列的规律也是相同的，这当然是正确的。
计算的时候，暴力计算每一张桌子的最远距离，当跨过行或列的对称轴是将它统一对称过来，特殊的，当行或列为偶数时，跨过对称轴行或列还要额外加一。
时间复杂度 \(O(n^2)\)。
比赛没有写出只算四分之一个矩形的程序，喜提最裂解，但是我这个方法比较好理解，也比较好写，最后奉上比赛时的代码。
\(Code\)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll s,t,n,m,r;
int main()
{
std::ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>s>>t;
for(int i=1;i<=t;i++)
{
bool p=1,q=1;
cin>>n>>m;
r=n*m;
if(n%2==0) n--,p=0;
if(m%2==0) m--,q=0;
r-=(n/2+1)*(m/2+1);
cout<<r<<" ";
if(p==0) n++;
if(q==0) m++;
if(n*m-r==1) {cout<<"0.000000000"<<endl; continue;}
long double ans=0.0;
long long k=1,j=1;
p=1,q=1;
for(k=1;k<=n;k+=2)
{
q=1;
for(j=1;j<=m;j+=2)
{
if(m%2==0&&j>(m/2)&&(q)) j++,q=0;
long long x,y;
if(k<=(n+1)/2) x=k;
else x=n-k+1;
if(j<=(m+1)/2) y=j;
else y=m-j+1;
// cout<<x<<" "<<y<<" ";
ans+=sqrtl(((long double)((n-x)*(n-x))+((long double)((m-y)*(m-y)))));
// cout<<" "<<ans<<" ";
}
if(n%2==0&&k+2>=(n/2)&&(p)) k++,p=0;
}
cout<<fixed<<setprecision(9)<<ans<<endl;
}
return (0-0);
}
