堆排序
创建最大堆：
用数组表示储存\(n\)个元素的堆时，叶子节点下标分别是\(\lfloor n/2 \rfloor\) , \(\lfloor n/2 \rfloor+1\) , \(\lfloor n/2 \rfloor+2\), ... , \(n-1\)。叶子节点没有孩子节点，其可视为满足堆性质的由单个节点构成的堆。
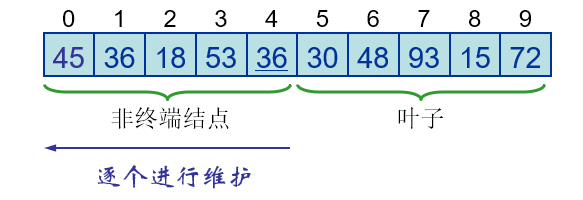
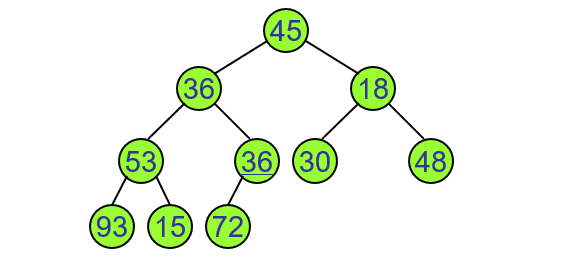
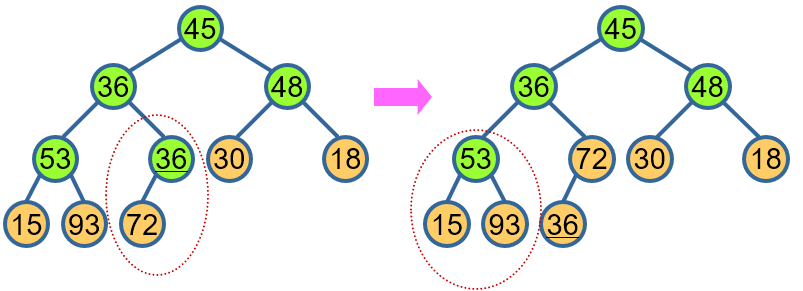
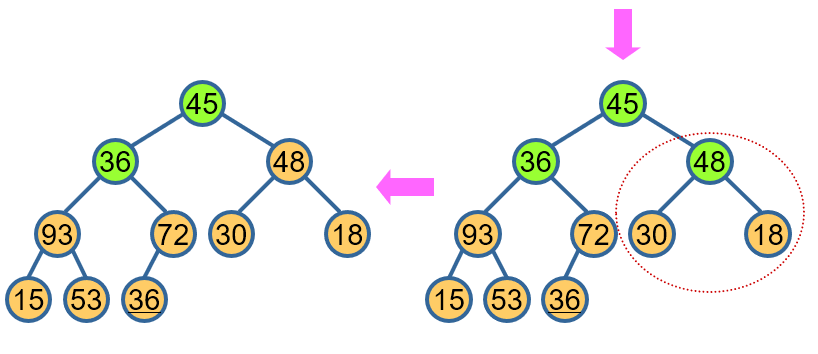
堆排序算法
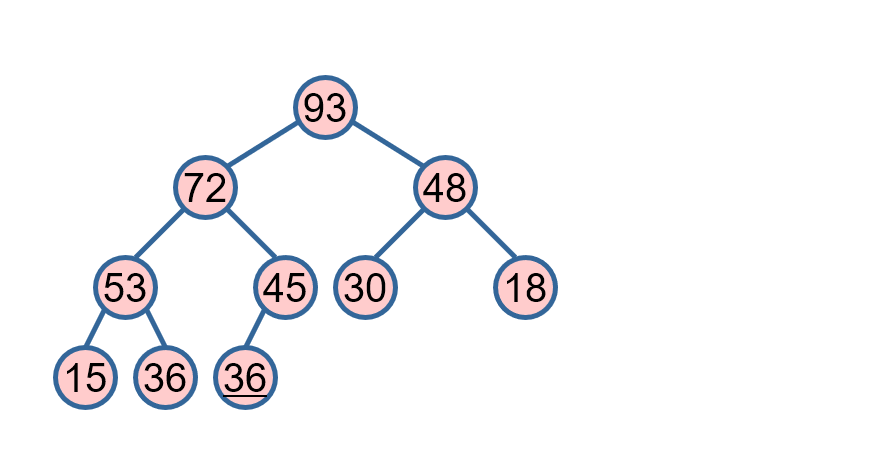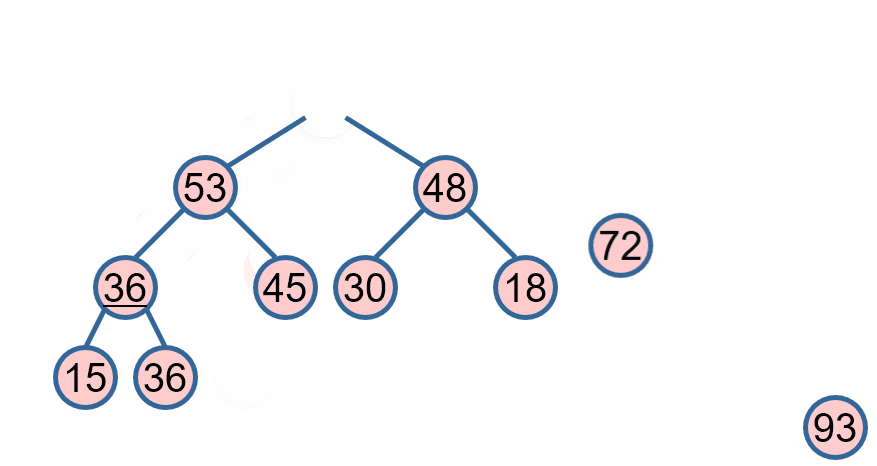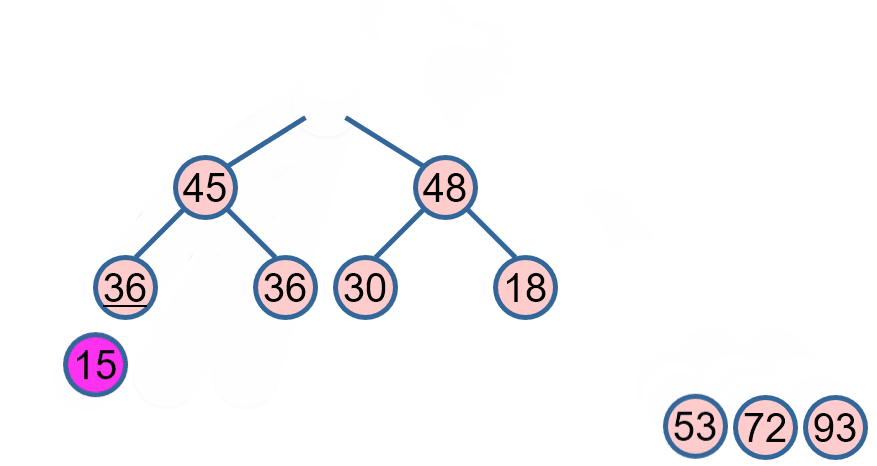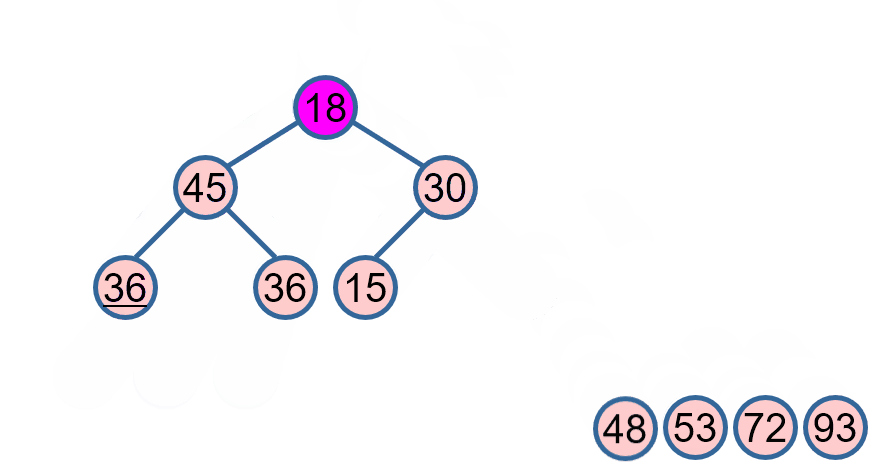
- 堆顶是排序区间最大的元素
- 去掉堆顶，将堆顶与堆的最后一个元素交换位置：
1 最大元素归位；
2 新树根不满足堆定义，维护成堆。
Java实现
import java.util.Arrays;
import java.util.Random;
public class HeapSort {
public static void main(String[] args) {
int[] A = new int[10];
Random rand= new Random();
for (int i = 0; i < A.length; i++) {
A[i]=Math.abs(rand.nextInt(100)) + 1;
}
// int[] A= {73, 89, 4, 99, 78, 91, 40, 68, 5, 25};
System.out.println("The Array Sort Before:\n" + Arrays.toString(A) + "\nsorting:");
HeapSort heapSort = new HeapSort();
heapSort.Sort(A);
}
int getParent(int i) {
//获得父节点
return i/2;
}
int getLeft(int i) {
//获得左孩子
return 2*i+1;
}
int getRight(int i) {
//获得右孩子
return 2*i+2;
}
void exchange(int[] A,int i,int j) {
//交换数组中的两个元素
int tempInt=A[i];
A[i]=A[j];
A[j]=tempInt;
}
void MaxHealthy(int[] A,int i,int heapSize) {
//维护A[i]为根的最大堆
int largest;
int l=getLeft(i);
int r=getRight(i);
if(l<heapSize&&A[l]>A[i])
largest=l;
else
largest=i;
if(r<heapSize&&A[r]>A[largest])
largest=r;
if(largest!=i) {
exchange(A, i, largest);
MaxHealthy(A, largest, heapSize);
}
}
void BulidMaxHeap(int[] A) {
//建堆
int heapSize=A.length;
for (int i = (A.length-1)/2; i >=0 ; i--)
MaxHealthy(A, i, heapSize);
}
void Sort(int[] A) {
int heapSize=A.length;
BulidMaxHeap(A);
System.out.println( Arrays.toString(A)+": 建最大根堆");
for (int i = A.length-1; i > 0; i--) {
exchange(A, 0, i);
heapSize--;
MaxHealthy(A, 0, heapSize);
System.out.println( Arrays.toString(A)+": 第"+(A.length-heapSize)+"回");
}
}
}
The Array Sort Before:
[1, 21, 96, 8, 36, 89, 68, 46, 50, 92]
sorting:
[96, 92, 89, 50, 36, 1, 68, 46, 8, 21]: 建最大根堆
[92, 50, 89, 46, 36, 1, 68, 21, 8, 96]: 第1回
[89, 50, 68, 46, 36, 1, 8, 21, 92, 96]: 第2回
[68, 50, 21, 46, 36, 1, 8, 89, 92, 96]: 第3回
[50, 46, 21, 8, 36, 1, 68, 89, 92, 96]: 第4回
[46, 36, 21, 8, 1, 50, 68, 89, 92, 96]: 第5回
[36, 8, 21, 1, 46, 50, 68, 89, 92, 96]: 第6回
[21, 8, 1, 36, 46, 50, 68, 89, 92, 96]: 第7回
[8, 1, 21, 36, 46, 50, 68, 89, 92, 96]: 第8回
[1, 8, 21, 36, 46, 50, 68, 89, 92, 96]: 第9回
——@guoyangde http://www.cnblogs.com/LittleTreasureBox/p/8904016.html
