Abnormal Detection(异常检测)和 Supervised Learning(有监督训练)在异常检测上的应用初探
1. 异常检测 VS 监督学习
0x1:异常检测算法和监督学习算法的对比

总结来讲:
1. 在异常检测中,异常点是少之又少,大部分是正常样本,异常只是相对小概率事件 2. 异常点的特征表现非常不集中,即异常种类非常多,千奇百怪。直白地说:正常的情况大同小异,而异常各不相同。这种情况用有限的正例样本(异常点)给有监督模型学习就很难从中学到有效的规律
0x2:常见的有监督学习检测算法
这块主要依靠庞大的打标样本,借助像DLearn这样的网络对打标训练样本进行拟合
0x3:常见的异常检测算法
- 基于模型的技术:这种异常检测技术首先建立一个数据模型,并基于已知样本进行"训练"得到一组模型参数,在之后的预测中所谓的异常点就是那些同模型不能完美拟合的对象。例如,高斯正态分布中左右两边偏离3倍标准差的点可以大概率认为是一个异常点
- 基于邻近度的技术(距离度量):通常可以在对象之间定义邻近性度量,异常对象是那些远离大部分其他对象的对象。当数据能够以二维或者三维散布图呈现时,可以从视觉上检测出基于距离的离群点。
- 基于密度的技术:对象的密度估计可以相对直接计算,特别是当对象之间存在邻近性度量。低密度区域中的对象相对远离近邻,可能被看做为异常。
2. 打标训练样本的获取
0x1: 对安全领域的算法应用 - 打标数据的采集往往是真正麻烦却很重要的事情
有几种方法可以帮助我们尽可能地去获取到更多打标的安全攻击/入侵事件
1. 自己构造攻击数据(Inject fake malicious data into data storage) 2. 利用MFS/POWERSLPOIT等工具采集攻击日志(Employ commonly used attack tools) 3. 红蓝渗透测试团队参与测试,然后抓取日志(Red team manually pen-tests) 4. 简单保守规则: 面对一类检测问题,大多数情况下是这样的情况: 80%的分类非常明显,甚至肉眼都能看出,对这类问题只要采取保守策略应用一些简单粗暴的正则/统计规则即可将异常找出来,对这部分样本,在收集打标样本的时候可以稍微放宽规则,尽可能地获取多的打标正例样本 5. 样本扩增(Synthetic Minority Oversampling Technique (SMOTE)): 我们可以理解为SMOTE对不平衡的数据集分配了不同的权重,为了弥补数据集中出现几率较小的那部分数据集对训练过程的影响,它往往会在过程中多次重复地抽取那部分小样本集来参与训练,从而一定程度上弥补数量少带来的问题
Relevant Link:
https://software.oreilly.com/learning/strategies-to-validate-your-security-detections?log-in http://contrib.scikit-learn.org/imbalanced-learn/auto_examples/index.html#dataset-examples https://en.wikipedia.org/wiki/Oversampling_and_undersampling_in_data_analysis https://en.wikipedia.org/wiki/Undersampling https://github.com/scikit-learn-contrib/imbalanced-learn https://www.jair.org/media/953/live-953-2037-jair.pdf https://gerardnico.com/wiki/data_mining/anomaly_detection
3. 有监督学习异常检测
1. A Character-Level Convolutional Neural Network with Embeddings + CNN
0x1: data prepare
1. 黑白样本收集
对于进程异常事件来说,白样本很好获取,直接根据全量进程事件group by,取top 5000的事件,几乎100%都是正常进程事件,因为偶发性的攻击事件和庞大的正常运维事件来说只是占很小的一部分。黑样本的获取就是一个相对来说的难题了,我们只能根据已知的攻防经验总结出一些攻击场景化的异常事件模型来提供黑样本,然后尽可能地去提高神经网络模型的泛化能力
2. 特殊字符归一化处理
在进程事件中,可能会遇到中文等特殊字符,对于这个问题,我的思路过程是这样的
1. 采用ascii 0 - 255编码,这样我的字符维度只有256,但是对非ascii字符只能归一化为"*"星号,这是一种"失真降维",即丢失了一部分原始输入字符串的信息 2. 采用utf-8编码,那样所有的字符都可以得到有效的编码化,但是带来一个更严重的问题是,因为大多数的进程事件字符串都是纯英文的,而仅仅有少数的非ascii参杂其中,所以我们用utf8编码化后,整个进程事件字符串vector出现了很明显的"稀疏特性",这种稀疏特性严重影响了后面神经网络模型对细节特征的提取
所以最终我把非ascii字符都编码为了星号
def sequence(string,maxlen=200): tokens = [] for c in string: if not c in printable: tokens.append(printable.index("*")) tokens.append(printable.index(c)) tokens = tokens[-maxlen:] if len(tokens) < maxlen: tokens = [0]*(maxlen-len(tokens))+tokens return tokens
在代码中可以看到,对长度不足的字符串也进行了padding处理
0x2: Architecture
1. Character Embedding
模型的第一层是一个带raw input length归一化的词向量嵌入模型,我们将我们的输入(进程事件字符串: 父进程 + 子进程命令行)归一化后,截断/padding为一个定长的s length字符串,然后投影到一个32维度的emberding空间中,在这个32维的emberdding空间中,字符串中的每一个字符都代表了一个向量(v1, v2, ...v32),从而整个输入字符串被转化为了一个s x 32的张量,张量可以理解为一个多位数组
Embedding layer is optimized jointly with the rest of the model through backpropagation, optimizing the individual characters’ embedding vectors to be more reflective of their semantic meaning, resulting in pairs of semantically similar characters being embedded closer to each other if they have similar attributes
emberdding词向量嵌入层在之后的模型train过程中,也会接收到BP反向传播带来的影响,从而不断调整词向量参数,最终的效果是使得emberding中的词向量权重更加拟合训练集,同一方向的词序列更加切进一个个有意义的进程事件,例如
1. 形成有意义的windows、linux盘符 2. 形成有意义的进程名 3. 形成有意义的指令字符串
In our implementation we set s = 200(输入进程事件字符串定长200) and m = 32(emberding维度32维)

def sum_1d(X): return K.sum(X, axis=1) def getconvmodel(filter_length,nb_filter): model = Sequential() model.add(Convolution1D(nb_filter=nb_filter, input_shape=(200,32), filter_length=filter_length, border_mode='same', activation='relu', subsample_length=1)) model.add(Lambda(sum_1d, output_shape=(nb_filter,)))
这里我们对(200, 32)的第二个维度,即emberdding 32维度进行了sumup降维
Relevant Link:
https://www.zhihu.com/question/51325408?from=profile_question_card
2. Feature Detection
到了这一层,我们的输入数据是一个s(200) x m(32)矩阵,我们接下要要利用深度神经网络来自动实现特征提取
特征提取阶段我们主要有2种结构组成
1. CNN卷积层: 1) 4个不同滤波窗口size的CNN卷积层(修正线性relu激活函数): Conv(np_filters=256, kernel_size=2/3/4/5, step_size=1) 2) sum: 根据emberdding降维 3) Dropout(0.5): 防止过拟合 2. SumPool: aggregate the results across the entire sequence by summing the kernels’ activations using SumPool K.sum(X, axis=1): 沿着emberdding的维度进行降维求和 sumup降维后的结果是一个 s(200) x vector(4 * 256 = 1024)的matrix,即每个向量是1024 verctor

注意到这里有4个不同np_filters的CNN,分别用size = 2/3/4/5长度的领域滤波去提取特征
并且这里使用了多输入的函数式编程,将4层不同滤波窗口大小的CNN进行merge操作,这个模型的损失函数将由4部分共同组成,这样做的好处是最大程序地提取并反映出原始输入数据的细节特征,即使其中一个损失函数的梯度发生弥散,来自其他CNN的损失函数的信息也能够训练Embeddding和CNN层。这体现了一种良好的正则化思想
在继续往下阐述之前,我们来稍微花一些时间计算一下这个merge CNN层的神经元个数 =
(200 - 2 + 1) * (32 - 2 + 1) * 256 + (200 - 3 + 1) * (32 - 3 + 1) * 256 + (200 - 4 + 1) * (32 - 4 + 1) * 256 + (200 - 5 + 1) * (32 - 5 + 1) * 256 = 5967360
CNN层的输出为1024维
这里我们来总结一下这样设计神经网络模型背后的意义
1. 每个卷积滤波器(不同kernel_szie)负责检测一组不同的相似序列模式,并通过sum_up其激活值得到一个最终的序列模式 2. 类比于图像滤波得到的像素纹理,如果我们用ascii的角度来看我们的文本字符串,这里学习到的特征本质也是一种"文本纹理" 我们得到了这些模式发生的程度 3. 选择CNN的另一个好处在于"特征子序列"可以出现在字符串中的任何位置,还依然能够被卷积检测到
3. 规范化
规范化的目的是解决样本量不足的问题,同时加速收敛、控制过拟合、可以少用或不用Dropout和正则、降低网络对初始化权重不敏感 、允许使用较大的学习率
可以选择使用层级别(layer wise)的BatchNormalization或者Dropout
4. Classification
使用fully connected Dense层来进行分类判断逻辑

每层的结构如下
middle = Dense(1024,activation='relu')(main_input) middle = Dropout(0.5)(middle) middle = BatchNormalization()(middle) middle = Dense(1024,activation='relu')(main_input) middle = Dropout(0.5)(middle) middle = BatchNormalization()(middle) output = Dense(1,activation='sigmoid')(middle) model = Model(input=main_input,output=output) model.compile(loss='binary_crossentropy', optimizer=optimizer) return model
在梯度下降算法中,我们寻则了adam算法,Adam可以理解为momutum SGD和RMSPROP的综合改进版本,同时引入了动态调整特性以及动量V特性。Adam(Adaptive Moment Estimation)本质上是带有动量项的RMSprop,它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后,每一次迭代学习率都有个确定范围,使得参数比较平稳。公式如下

Relevant Link:
https://keras-cn.readthedocs.io/en/latest/layers/normalization_layer/ https://github.com/joshsaxe/eXposeDeepNeuralNetwork/blob/master/src/modeling/models.py http://keras-cn.readthedocs.io/en/latest/layers/convolutional_layer/ http://www.cnblogs.com/LittleHann/p/6629069.html https://arxiv.org/pdf/1702.08568.pdf
2. Graph-based Intrusion Detection on Process Event
paper的主要设计思想是根据已有的异构事件数据,包括
1. 进程对文件的操作: 读/写文件 2. 进程对SOCKET的操作
从这些异构数据源抽象出一种代表了information flow(数据流动)的event事件,每个event都关联了两个实体entity,分别代表sender/reveiver的角色,例如
1. vim 1.txt:entityA(FILE) flow-> entityB(PROCESS) 2. http request:entityC(PROCESS) flow-> entityD(ISOCKET)
在生成graph的训练初期,需要先根据主机进程的归约性规律(进程可以打开文件(文件信息流到进程中)、进程写入文件(进程信息流到文件中)、进程不能打开进程),以及时间顺延序列来生成一些"候选路径",所有的候选路径生成一张有向无环图
接下来对所有路径上的每一条变edge,都计算sender/receiver的分值,每个有向edge的分值由训练样本中的该flow event发生的总时间窗口决定


举例来说,如果/usr/bn/httpd write /var/log/access.log是一个高频词事件,则该事件所代表的edge在整个训练集中的T(时间窗口)就会较大,相对的它的概率也较大,这也暗示着它是一个常规事件
而像vim /etcpasswd这种低频次事件,在训练样本集中就应该较少出现,反过来,这个事件的abnormal score就要越高

通过这种方法,我们基于训练集得到的事件information flow graph,来评估新的样本事件中哪些是疑似可疑事件,但是这里要注意的一个问题是,long term event sequence和short term event sequence的归一化,为了防止长序列的事件序列累加得到的异常分值过高问题,我们需要将所有分值根据path length进行归一化
Relevant Link:
https://arxiv.org/pdf/1608.02639.pdf https://github.com/corbinmcneill/Graph-Based-Network-Intrusion-Detection/tree/master/mr_code/GraphCreation/src/graphcreator http://www.freepatentsonline.com/20160330226.pdf http://www.freepatentsonline.com/y2016/0330226.html
4. 基于密度的异常检测
1. Intrusion Detection System using Unsupervised Neural Networks - GNG / SOM
相关讨论可参阅这篇文章
Relevant Link:
https://github.com/jnasante/IDS
5. 基于邻近度的异常检测
1. Isolation Forest Outlier Detection - 孤立森林 异常检测
iForest算法用于挖掘异常(Anomaly)数据,或者说离群点挖掘,是在一大堆数据中,找出与其它数据的规律不太符合的数据,异常数据的两个特征(少且不同: few and different)
1. 异常数据只占很少量; 2. 异常数据特征值和正常数据差别很大
iForest 适用与连续数据(Continuous numerical data)的异常检测,将异常定义为“容易被孤立的离群点 (more likely to be separated)”——可以理解为分布稀疏且离密度高的群体较远的点。用统计学来解释,在数据空间里面,分布稀疏的区域表示数据发生在此区域的概率很低,因而可以认为落在这些区域里的数据是异常的

iForest属于Non-parametric(无参数反馈调整训练)和unsupervised(无监督)的方法,即不用定义数学模型也不需要有标记的训练。
对于如何查找哪些点是否容易被孤立(isolated),iForest使用了一套非常高效的策略。、
假设我们用一个随机超平面(某一个维度切面)来切割(split)数据空间(data space), 切一次可以生成两个子空间(想象拿刀切蛋糕一分为二)。之后我们再继续用一个随机超平面来切割每个子空间,循环下去,直到每子空间里面只有一个数据点为止。
直观上来讲,我们可以发现那些密度很高的簇是可以被切很多次才会停止切割,但是那些密度很低的点很容易很早的就停到一个子空间了。
上图里面,红色点(离群点),就很容易被切几次就停到一个子空间,而白色/绿色的点(高频正常点) 需要切很多次才停止。
怎么来切这个数据空间是iForest的设计核心思想,由于切割是随机的,所以需要用ensemble的方法来得到一个收敛值(蒙特卡洛方法),即反复从头开始切,然后平均每次切的结果。iForest 由t个iTree(Isolation Tree)孤立树 组成,每个iTree是一个二叉树结构,其实现步骤如下:
1. 初始化IsolationForest的时候需要指定树(tree)的数量,实验发现,在100颗树的时候,路径的长度就已经覆盖得比较好了,因此选100颗也就够 2. 对于每一棵树,我们都重复以下过程 1) 从训练数据中随机选择Ψ个点样本点作为subsample(一般是无放回抽样),放入树的根节点。样,是为了更好的将正常数据和异常数据分离开来。有别于其它模型,采样数据越多,反面会降低iForest识别异常数据的能力。因为,通常使用256个样本,这也是scikit-learn实现时默认使用的采样数 2. 我们的输入样本可能是高维空间的向量数据,随机指定一个维度(attribute)(一棵tTree建树过程中的每一轮切分选取的维度都可能不一样),在当前节点数据中的这个维度(从这个维度的超平面去切)上的值计算[min, max],从[min, max]中随机产生一个切割点p,切割点产生于当前节点数据中指定维度的最大值和最小值之间,相当于用一个超平面去对当前节点的数据集进行切割 3) 以此切割点生成了一个超平面,然后将当前节点数据空间划分为2个子空间 3.1) 把指定维度里小于p的数据放在当前节点的左孩子 3.2) 把大于等于p的数据放在当前节点的右孩子 4) 在孩子节点中递归步骤2和3,不断构造新的孩子节点,直到 孩子节点中只有一个数据(无法再继续切割) 或 孩子节点已到达限定高度(例如: log2(ψ)) 3. 获得t个iTree之后,iForest 训练就结束,然后我们可以用生成的iForest来评估测试数据了
可以看到,我们在C语言课上学的二叉树排序算法,本质上就是一个1-d向量数据的tTree建树过程,但是在大数据分析中,高维/超高维数据是很常见的情况,因此我们才需要在建二叉树的过程中随机地选取不同维度的超平面(随机森林思想)进行二分分类。我个人对iForest算法背后体现的思想的理解是这样的
# 先用1-d维数据点说明 摆在我们面前有大堆大小不等的小球,例如有: [6, 6.1, 6.2, 5.9, 5.8, 6.3, 6.4, 6.5, 33]这些大小直径的小球,我们拿到的任务是把这些小球尽量地去平分为大小相同的堆,如果分到最后一堆中只剩一个球了,就停止分类。 我们发现从这里面随机选取一个值作为切分点,例如5.9,则33立刻就被分到"大于切分点"那一类,并且在第一轮就停止了分类,这体现的是如果输入样本数据中孤立点是"少且数值突兀的",则这类数据点有更大的可能在很短的时间内停止切分。 我们还注意到一点,由于孤立点是偶发小比例的数值点,则在随机选择切分点的时候,孤立点有更大的几率被选在切分点的另一侧,从而停止分类 # >=2维数据点 高维数据的情况要更复杂一些,在一个广场上有一大群人,它们每个人都有3个属性(即3个维度): [肤色, 年龄, 性别],我们假设广场上大部分都是白种人,21-22岁之间的年轻女性,但是其中混杂了2个黑人男性,分别是21岁和23岁。 我们随机选取其中一个维度: 肤色,然后大喊一声,白种人站左边,黑种人站右边。这时那2个黑人男性就立刻被分类到了右子树。 在第二轮的分类中,我们选取年龄作为超平面切分,选择22岁最为切分点,这时左子树中又进行了一次切分,右子树的那2个黑人男性被分成了2颗叶子,并且停止了继续的切分 可以看到,只要输入数据本身确实存在孤立离群特性,这这些数据点有"更大的概率被尽早的分到叶子中"
获得t个iTree之后,iForest 训练就结束,然后我们可以用生成的iForest来评估测试数据了。对于一个输入数据x,我们令其遍历每一棵iTree,然后计算x最终落在每个树第几层(x在树的高度)。然后我们可以得出x在每棵树的高度平均值,即 the average path length over t iTrees。
获得每个测试数据的average path length后,我们可以设置一个阈值(边界值)
1. average path length 低于此阈值的测试数据即为异常。也就是说 “iForest identifies anomalies as instances having the shortest average path lengths in a dataset ”(异常在这些树中只有很短的平均高度). *值得注意的是,论文中对树的高度做了归一化,得出一个0到1的数值 1) 如果分数越接近1,其是异常点的可能性越高 2) 如果分数都比0.5要小,那么基本可以确定为正常数据 3) 如果所有分数都在0.5附近,那么数据不包含明显的异常样本 2. 未归一化前,样本在森林中平均高度越高,则说明该数据有越大可能属于
4个测试样本遍历一棵iTree的例子如下

b和c的高度为3,a的高度是2,d的高度是1。可以看到d最有可能是异常,因为其最早就被孤立(isolated)了
生成一棵iTree的详细算法

X为独立抽取的训练样本。参数e的初始值为0。h是树可以生成的最大高度。iForest算法默认参数设置如下
subsample size: 256 Tree height: 8 Number of trees: 100
code
# -*- coding: utf-8 -*- import numpy as np import matplotlib.pyplot as plt from sklearn.ensemble import IsolationForest pointerDim = 2 rng = np.random.RandomState(42) # Generate train data X = 0.3 * rng.randn(256, pointerDim) # 100 2-d pointer #print X # 得到一个相对距离为4个族群 X_train = np.r_[X + 2, X - 2] # Generate some regular novel observations # 测试集和训练集采用同样的方法产生2个族群 X = 0.3 * rng.randn(52, pointerDim) # 20 2-d poineter X_test = np.r_[X + 2, X - 2] # Generate some abnormal novel observations # 随机产生20个[-4,4]随机点 X_outliers = rng.uniform(low=-4, high=4, size=(52, pointerDim)) # fit the model clf = IsolationForest(max_samples=100, random_state=rng) clf.fit(X_train) # clf.predict直接返回iForest对数据点的"离群"判断结果 y_pred_train = clf.predict(X_train) y_pred_test = clf.predict(X_test) y_pred_outliers = clf.predict(X_outliers) print "y_pred_train" print y_pred_train print "y_pred_test" print y_pred_test print "y_pred_outliers" print y_pred_outliers # plot the line, the samples, and the nearest vectors to the plane # 构建整个50 * 50的网格点 xx, yy = np.meshgrid(np.linspace(-5, 5, 50), np.linspace(-5, 5, 50)) print "np.c_[xx.ravel(), yy.ravel()]" print np.c_[xx.ravel(), yy.ravel()] # 不直接进行预测,只让模型输出异常分值 Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()]) print "len(Z)" print len(Z) print "Z[0]" print Z[0] print "xx.shape" print xx.shape # 将2500-d异常分值vector拉伸为50 * 50的异常分值matrix Z = Z.reshape(xx.shape) print "Z" print Z plt.title("IsolationForest") # 这里只是将整个50 * 50网格化,并计算每一个点和聚类中心的相关度(离群指数),越靠近同一类,相似度越高,分值越高,颜色越淡; plt.contourf(xx, yy, Z, cmap=plt.cm.Blues_r) b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white') b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='green') c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='red') plt.axis('tight') plt.xlim((-5, 5)) plt.ylim((-5, 5)) plt.legend([b1, b2, c], ["training observations", "new regular observations", "new abnormal observations"], loc="upper left") plt.show()
Relevant Link:
http://www.jianshu.com/p/1b020e2605e2 https://zhuanlan.zhihu.com/p/25040651 http://www.tk4479.net/ssw_1990/article/details/71436714 http://qf6101.github.io/machine%20learning/2015/08/01/Isolation-Forest http://www.17bigdata.com/%E5%BC%82%E5%B8%B8%E6%A3%80%E6%B5%8B%E7%AE%97%E6%B3%95-isolation-forest.html http://scikit-learn.org/stable/auto_examples/ensemble/plot_isolation_forest.html#sphx-glr-auto-examples-ensemble-plot-isolation-forest-py
2. unsupervised-machine-learning-with-one-class-support-vector-machines - 单分类SVM无监督聚类
one-class SVM特别适合黑白样本严重不平衡的检测场景下,例如安全入侵检测中,白样本数量非常多且很容易得到,但是代表异常事件的黑样本本身就很少(入侵是偶发事件)且即使是有限的黑样本也强依赖安全人员的分析经验来通过正则规则的方式缓慢积累
one-class svm针对白样本进行聚类,得到一个分类边界。即one-class svm主要学习的是尽可能地学习到白样本的边界,然后之后预测时采取"非黑即白"的策略,将边界外的标记为可疑样本
0x1: scikit-learn实现的one-class svm demo
# -*- coding: utf-8 -*- import numpy as np import matplotlib.pyplot as plt import matplotlib.font_manager from sklearn import svm if __name__ == '__main__': xx, yy = np.meshgrid(np.linspace(-5, 5, 500), np.linspace(-5, 5, 500)) # Generate train data X = 0.3 * np.random.randn(100, 2) X_train = np.r_[X + 2, X - 2] # Generate some regular novel observations X = 0.3 * np.random.randn(20, 2) X_test = np.r_[X + 2, X - 2] # Generate some abnormal novel observations X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2)) # fit the model clf = svm.OneClassSVM(nu=0.1, kernel="rbf", gamma=0.1) clf.fit(X_train) y_pred_train = clf.predict(X_train) y_pred_test = clf.predict(X_test) y_pred_outliers = clf.predict(X_outliers) n_error_train = y_pred_train[y_pred_train == -1].size n_error_test = y_pred_test[y_pred_test == -1].size n_error_outliers = y_pred_outliers[y_pred_outliers == 1].size # plot the line, the points, and the nearest vectors to the plane Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) plt.title("Novelty Detection") plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 7), cmap=plt.cm.PuBu) a = plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='darkred') plt.contourf(xx, yy, Z, levels=[0, Z.max()], colors='palevioletred') s = 40 b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white', s=s) b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='blueviolet', s=s) c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='gold', s=s) plt.axis('tight') plt.xlim((-5, 5)) plt.ylim((-5, 5)) plt.legend([a.collections[0], b1, b2, c], ["learned frontier", "training observations", "new regular observations", "new abnormal observations"], loc="upper left", prop=matplotlib.font_manager.FontProperties(size=11)) plt.xlabel( "error train: %d/200 ; errors novel regular: %d/40 ; " "errors novel abnormal: %d/40" % (n_error_train, n_error_test, n_error_outliers)) plt.show()

0x2:参数优化 - 选择
one-class svm对数据集数量、数据是否归一化、核函数参数选择都非常敏感,调优的过程需要仔细的思考和不断地尝试
SVM模型有两个非常重要的参数C与gamma
1. C是惩罚系数,即对误差的宽容度 1) c越高,说明越不能容忍出现误差,但是容易过拟合 2) C越小,容易欠拟合 3) C过大或过小,泛化能力变差 2. gamma是选择RBF函数作为kernel后,该函数自带的一个参数。隐含地决定了数据映射到新的特征空间后的分布 1) gamma越大,支持向量越少,运算速度越快 2) gamma值越小,支持向量越多 3) 支持向量的个数影响训练与预测的速度
RBF公式里面的sigma和gamma的关系如下

gamma的物理意义是RBF(高斯核)的幅宽,它会影响每个支持向量对应的高斯的作用范围,从而影响泛化性能
如果gamma设的太大,会很小,
很小的高斯分布长得又高又瘦, 会造成只会作用于支持向量样本附近,对于未知样本分类效果很差(过拟合)
如果gamma设的过小,会很大,则会造成平滑效应太大,无法在训练集上得到特别高的准确率,也会影响测试集的准确率。
RBF核应该可以得到与线性核相近的效果(按照理论,RBF核可以模拟线性核),可能好于线性核,也可能差于,但是,不应该相差太多。
当然,很多问题中,比如维度过高,或者样本海量的情况下,大家更倾向于用线性核,因为效果相当,但是在速度和模型大小方面,线性核会有更好的表现。
Relevant Link:
http://rvlasveld.github.io/blog/2013/07/12/introduction-to-one-class-support-vector-machines/ http://scikit-learn.org/stable/auto_examples/svm/plot_oneclass.html#sphx-glr-auto-examples-svm-plot-oneclass-py https://thisdata.com/blog/unsupervised-machine-learning-with-one-class-support-vector-machines/ http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html http://blog.sina.com.cn/s/blog_6a41348f0101ep7w.html http://blog.sina.com.cn/s/blog_57a1cae80101bit5.html http://blog.csdn.net/bryan__/article/details/51506801 http://scikit-learn.org/stable/auto_examples/svm/plot_rbf_parameters.html
6. 基于模型(分布建模)的异常检测
0x1:一元高斯分布异常检测
不管我们的特征集合中有多少特征,一元高斯分布模型要求我们“一次一个”进行“特征变量异常分析”。
1. 正态分布介绍
正态分布又名高斯分布,是一个在数学,物理以及工程等领域都非常重要的概率分布。由于这个分布函数有很多漂亮的性质,使得其在诸多设计统计科学离散科学等许多领域都有着重大的影响力。
若随机变量X服从一个位置参数为 μμ 尺度参数为 σσ 的概率分布,记为: ![]()
则其概率密度函数为

正态分布的数学期望值或期望值 μ 等于位置参数,决定了分布的位置;
其方差 σ2 的开平方或标准差 σ 等于尺度参数,决定了分布的幅度。
不同参数的正态分布图:

2. 正态分布的一些特性
1. 密度函数关于平均值对称 2. 函数曲线下68.268949%的面积在平均数左右的一个标准差 σ 范围内。 3. 函数曲线下95.449974%的面积在平均数左右两个标准差 2σ 的范围内。 4. 函数曲线下99.730020%的面积在平均数左右三个标准差 3σ 的范围内。 5. 函数曲线下99.993666%的面积在平均数左右四个标准差 4σ 的范围内。
高斯分布的这些特性可以作为异常统计的依据。
在正态分布的假设下,区域 μ±3σ 包含了99.7% 的数据,如果某个值距离分布的均值 μ 超过了3σ,那么这个值就可以被简单的标记为一个异常点(outlier)。
3. 基于一元正态分布的离群点检测方法
假设 n 维的数据集合形如![]() ,那么可以计算每个维度的均值和方差μj,σj,j∈{1,...,n}。
,那么可以计算每个维度的均值和方差μj,σj,j∈{1,...,n}。
具体来说,对于j∈{1,...,n},可以计算

在正态分布的假设下,如果有一个新的数据 x⃗ ,可以计算概率 p(x⃗ ) 如下:

根据概率值的大小就可以判断 x 是否属于异常值。
4. 使用一元高斯分布进行异常统计前需要关注的问题
读者需要特别注意的是,在使用高斯分布进行异常统计前,我们需要先关注一下我们的数据本身是否满足一定的分布。
1)样本数量 N
小样本 N 条件下,大数定理本身都不一定能成立,数据的出现带有很强的随机性,因此,在小样本 N 条件下,使用高斯分布得到的异常统计,会更容易出现误报。
2)样本本身是否符合“正态特性”
下图是一个一元统计量的观测值。

可以看到,数据集的分布集中在了横轴的两头。
这个case是笔者在项目中遇到的一个实际案例,真实的情况是,大部分的“正常”样本集中在横轴的低值域区域,而我们要检测的少部分“异常”样本集中在横轴的高值域区域。
显然,这部分高值域区域的点集就是我们要检测的异常点,但是问题来了,在这种分布下,计算出来的 均值 会落在中间的区域(很容易想象出来),这样,两头的数据点都成了所谓的异常点,无法达到我们想要的效果。
出现这种情况的原因是什么呢?首先,样本量 N 不够肯定是罪魁祸首;其次,在很多情况下,异常点和正常点的关系并不是“对称的高斯分布”,而是单边高斯分布。用传统的双边高斯分布的统计方法来进行数据建模(统计高斯模型)肯定是不行的。
5. 一个基于文件创建时间孤立点的异常统计Project - 无监督异常统计
1)目标数据规律探查
对于webshell来说,存在以下几种异常的情况:
1. 文件夹本身保存的是正常的网站文件,突然某天出现了少量恶意shell文件 2. 整个文件夹本身就是一个“马场”,布满了shell文件 3. 文件夹本身保存的是正常的网站文件,但是被黑客重复入侵,文件夹下充斥了大量的恶意shell文件,数量甚至超过了原始的正常文件数量
通过散点图描述:
第一种情况:基于样本偏离均值的程度进行判断,可以进行有效建模

第二种情况:方差本身超过一定阈值就可以作为一个二分类决策指标,但是如果该文件夹下存在正常文件,要研究下用什么统计把它们筛选出来。可以采取统计文件create_time小于均值两侧范围内多少%比认为是正常的。

2)特征向量线性可分特性探查
在开始建模之前,我们需要先探查目标样本的几个问题:
1. 单个维度是否都具备线性可分特征。如果存在这种特征,则说明找到了“强特征”!恭喜你!简单一个where条件就可以完成你的二分类目标了。一个感知机神经元判别器就可以搞定。
2. 单个特征维度都无法做到线性可分,但是多个组合特征之间可以通过复合线性函数进行有效二分类。这个时候要么通过专家经验编写多个if-else条件,或者直接训练一个有监督二分类模型,例如随机森林,进行二分类
3)分布模型异常统计的局限
分布统计模型能够work的一个前提是:目标样本数据需要在某一些特征维度上呈现出一定的“分布特性”。如果这个前提不成立,异常统计是无法进行的。
笔者一个典型的场景是:SEO批量插马/挂马模式。
SEO恶意文件会对目标文件夹进行遍历,对所有文件都插入一段恶意shellcode;或者新建一个文件夹,在该文件夹下恶意shell文件。
这种行为导致的结果就是,该文件夹下所有文件的file_create_time都相同,看起来和正常的业务文件夹在统计分布上是一样的,无法区分。
4)特征工程
1. 基础统计特征 -- file md5 whole aliyun ecs statistic info a.uuid_cn_by_md5, a.aliuid_cn_by_md5, a.path_cn_by_md5, -- file path whole aliyun ecs statistic info uuid_cn_by_path, aliuid_cn_by_path, md5_cn_by_path, -- directory statistic info b.path_cn_by_directory, b.md5_cn_by_directory, b.fileext_cn, b.avg_file_create, b.stddev_file_create, b.median_file_create, b.avg_uuid_cn_by_md5, b.stddev_uuid_cn_by_md5, b.median_uuid_cn_by_md5, b.avg_aliuid_cn_by_md5, b.stddev_aliuid_cn_by_md5, b.median_aliuid_cn_by_md5, b.avg_path_cn_by_md5, b.stddev_path_cn_by_md5, b.median_path_cn_by_md5, b.avg_uuid_cn_by_path, b.stddev_uuid_cn_by_path, b.median_uuid_cn_by_path, b.avg_aliuid_cn_by_path, b.stddev_aliuid_cn_by_path, b.median_aliuid_cn_by_path, b.avg_md5_cn_by_path, b.stddev_md5_cn_by_path, b.median_md5_cn_by_path, -- gaussion statistic between file and directory ABS(a.file_create_int - b.avg_file_create) AS file_create_by_avg_distance, ABS(a.uuid_cn_by_md5 - b.avg_uuid_cn_by_md5) AS uuid_cn_by_md5_by_avg_distance, ABS(a.aliuid_cn_by_md5 - b.avg_aliuid_cn_by_md5) AS aliuid_cn_by_md5_by_avg_distance, ABS(a.path_cn_by_md5 - b.avg_path_cn_by_md5) AS path_cn_by_md5_by_avg_distance, ABS(a.uuid_cn_by_path - b.avg_uuid_cn_by_path) AS uuid_cn_by_path_by_avg_distance, ABS(a.aliuid_cn_by_path - b.avg_aliuid_cn_by_path) AS aliuid_cn_by_path_by_avg_distance, ABS(a.md5_cn_by_path - b.avg_md5_cn_by_path) AS md5_cn_by_path_by_avg_distance 2. 加工特征: 本质上和DNN隐层中的扭曲效果类似 -- 表征了距离高斯均值中心的距离和标准差的比例,通过构造特征进行回归拟合,可以避免手工调整 N 倍或 N.N倍 标准差的繁杂过程 file_create_by_avg_distance / stddev_file_create uuid_cn_by_md5_by_avg_distance / stddev_uuid_cn_by_md5 aliuid_cn_by_md5_by_avg_distance / stddev_aliuid_cn_by_md5 path_cn_by_md5_by_avg_distance / stddev_path_cn_by_md5 uuid_cn_by_path_by_avg_distance / stddev_uuid_cn_by_path aliuid_cn_by_path_by_avg_distance / stddev_aliuid_cn_by_path md5_cn_by_path_by_avg_distance / stddev_md5_cn_by_path 3. 归一化特征 -- 标准差依赖于数据本身的scale,可能不能充分说明问题。使用标准离差率(标准差除以平均值)来更客观评价离群程度 b.stddev_file_create / b.avg_file_create, -- b.stddev_uuid_cn_by_md5 / b.avg_uuid_cn_by_md5, b.stddev_aliuid_cn_by_md5 / b.avg_aliuid_cn_by_md5, b.stddev_path_cn_by_md5 / b.avg_path_cn_by_md5, b.stddev_uuid_cn_by_path / b.avg_uuid_cn_by_path, b.stddev_aliuid_cn_by_path / b.avg_aliuid_cn_by_path, b.stddev_md5_cn_by_path / b.avg_md5_cn_by_path,
5)特征重要性评估
使用autoXGB进行自动特征重要性评估得到结论如下:
original_name feature_name feature_importance path_cn_by_md5: 3889.0: 该文件的md5在全网出现的路径path数量, 体现了该文件可能被不同的人使用分发到不同路径下 path_cn_by_directory: 3350.0: 该文件所在的目录下文件数 md5_cn_by_directory: 2862.0: 该文件所在的目录下文件数 uuid_cn_by_md5: 2741.0: 该文件的md5在全网多少uuid出现,对于批量抓鸡黑客来说,常常会使用同一个webshell批量传播到大量的机器上 cv_path_cn_by_md5: 2658.0: 一个目录下所有文件的md5散步path广度,如果标准离差很大, 说明可能出现了可疑文件 median_path_cn_by_md5: 2494.0: path_cn_by_md5_outlier_rate: 2466.0: 文件的md5在全网出现的路径path数量这个指标和该文件所在目录的均值高斯异常比值。 aliuid_cn_by_md5: 2396.0: 该文件的md5在全网多少aliuid出现 avg_path_cn_by_md5: 2370.0 stddev_path_cn_by_md5: 2111.0 path_cn_by_md5_by_avg_distance: 2079.0 file_create_by_avg_distance: 1903.0: 该文件的创建时间和该目录下所有文件的平均创建时间均值的差值 cv_aliuid_cn_by_md5: 1639.0 median_uuid_cn_by_md5: 1589.0 uuid_cn_by_md5_outlier_rate: 1554.0 cv_uuid_cn_by_md5: 1530.0 avg_uuid_cn_by_md5: 1484.0 file_create_outlier_rate: 1464.0: 文件创建时间孤立程度离群率 median_aliuid_cn_by_md5: 1387.0 stddev_uuid_cn_by_md5: 1383.0 aliuid_cn_by_md5_outlier_rate: 1368.0 uuid_cn_by_md5_by_avg_distance: 1311.0 aliuid_cn_by_md5_by_avg_distance: 1272.0 stddev_aliuid_cn_by_md5: 1268.0 avg_aliuid_cn_by_md5: 1257.0 path_cn_by_md5_outlier_rate_cv: 758.0 cv_md5_cn_by_path: 561.0 avg_md5_cn_by_path: 547.0 stddev_md5_cn_by_path: 487.0 md5_cn_by_path_by_avg_distance: 441.0 uuid_cn_by_md5_outlier_rate_cv: 407.0 aliuid_cn_by_md5_outlier_rate_cv: 400.0 fileext_cn: 380.0 uuid_cn_by_path: 275.0 md5_cn_by_path: 251.0 median_md5_cn_by_path: 212.0 avg_uuid_cn_by_path: 186.0 md5_cn_by_path_outlier_rate: 179.0 cv_uuid_cn_by_path: 135.0 aliuid_cn_by_path: 123.0 uuid_cn_by_path_by_avg_distance: 119.0 median_uuid_cn_by_path: 116.0 cv_aliuid_cn_by_path: 111.0 aliuid_cn_by_path_by_avg_distance: 109.0 avg_aliuid_cn_by_path: 83.0 stddev_uuid_cn_by_path: 82.0 stddev_aliuid_cn_by_path: 73.0 median_aliuid_cn_by_path: 68.0 aliuid_cn_by_path_outlier_rate: 49.0 uuid_cn_by_path_outlier_rate: 48.0 md5_cn_by_path_outlier_rate_cv: 22.0 aliuid_cn_by_path_outlier_rate_cv: 18.0 uuid_cn_by_path_outlier_rate_cv: 14.0
笔者在对大数据组件分析进行人工分析的时候,发现了几个有趣的现象:
1. 再次体会到:数据中蕴含着规律!有时候这种规律甚至超过了专家的认知,比如上面的特征排序有几个维度是令我一开始感到惊讶的,但是仔细一分析又可以理解。 2. 专家经验还是靠谱的,整体上看,xx_by_path这个维度的特征,笔者在提取的时候,根据网络安全从业的经验,就已经认为是重要性不高的,组件分析出来的结果和我的预期是一致的。 3. xx_by_md5特征比较靠前,基本上说明一个md5是可以唯一代表一个唯一文件的依据。 4. md5文件的全网分布广度特征排名比较靠前 ,这再次证明了大数据情况下,是有机会获得比单机日志更好的分类效果,大数据的优势是能看到上帝视角!一定要多思考大数据的优势!不单单是数据量大,而是大数据本身! 5. 高斯统计分布的离群特征确实有很强的表征能力,此类特征的排名也比较靠前。
Relevant Link:
https://blog.csdn.net/Gamer_gyt/article/details/76692188 https://blog.csdn.net/wyl1813240346/article/details/79059647 https://cloud.tencent.com/developer/article/1054267
0x2:多元高斯分布异常检测
我们通过一个例子来说明为什么需要多元高斯分布模型而不是多个单元高斯分布模型的混合模型(boosting思路)
假设在数据中心监控机器的例子中,我们有如下的内存和CPU使用数据:

其中对于这两个维度的数据(分别做投影),都服从正态分布:

如果现在在我们的测试集中,有一个异常数据点出现在下图的位置中:

那么在这种情况下我们会发现,这一点对应的两个维度下的概率(分别对两个维度做投影)其实都不低,从单维度p(x)的结果上,我们无法准确预测这个样本是否属于异常。
产生这个问题的实际原因其实是从x1和x2这两个维度来看,我们的正常数据和"异常点数据"都处在一个高概率区间内
为了解决这个问题,要用到多元高斯分布(多元正态分布)
1. 多元高斯分布数学模型
在多元高斯分布中,对于n维特征x∈Rn,不要把模型p(x1),p(x2),....,p(xn)分开,而要建立p(x)整体的模型。
多元高斯分布的参数包括一个均值向量 u 和一个 n * n 的协方差矩阵:
带入之后计算 p(x)概率分布: ,公式中
,公式中 这一项,代表了协方差矩阵的行列式
这一项,代表了协方差矩阵的行列式
2. 多元高斯分布图像
我们来对比一下不同的 u 和不同的 Σ 组合后,对应的p(x)的形状

表格从上到下依次是三种情况对应的参数、三维图像以及俯视图。从图中可以看出
1. 3个高斯分布在x1和x2维度的投影都是以0为中心的高斯分布(钟形曲线),这是因为它们的均值向量 u 都是0 2. 当缩小协方差时,中心区域的凸起就会变得更细长 3. 当扩大协方差时,中心区域的凸起就会变得更扁
接下来我们尝试对协方差中使用不同的数值分量,来观测p(x)形状的变化

可以看:
1. 当我们缩小x1的值,而x2保持原来不变时,相当于是对特征x1的方差进行了缩小,所以图像在x1的方向上会显得更细长 2. 当我们放大x1的值,而x2保持原来不变,相当于是对特征x1的方差进行了放大,所以图像在x1的方向上会显得更扁平
我们继续通过改变协方差Σ非对角线上的元素来得到不同的高斯分布:

可以看出来,当我改变了非对角线上元素的值时,p(x)p(x)的图像也变得倾斜了;当我增大了这些元素时,这个倾斜的分布图像变得更细长了。
我们继续把非对角线上元素设置为负数

可以看到图像朝反方向倾斜
如果我们改变µ,图像p(x)会在对应为维度方向上平移

可以看到,多元高斯分布有很多好处
1. 它可以将多个维度的变量综合到一个公式中得到一个平滑的概率值 2. 它能够让我们了解到两个特征变量之间存在的正相关或者负相关性(这通过协方差矩阵左右对角线的值得以体现)
3. 多元高斯分布如何进行异常检测?
模型训练 - 得到参数估计
在进行预测之前,我们需要对我们定义的多元高斯模型进行参数拟合训练(即参数估计)
假设我们有如下的训练样本

- 首先,用我们的训练集来拟合模型p(x),得到参数µ和Σ:模型的参数由训练数据的均值向量和协方差矩阵组成,高斯模型的模型参数直接由训练数据计算而来

到这一步为止,我们得到的反映训练数据(一组特征维度组合)的高斯分布,也可以理解为得到了一个 f(x)函数,这个函数可以将新输入的特征向量转化为一个高斯概率值
模型预测(预测函数)
- 然后,当你得到一个新的测试样本时,只需要传入二元变量:(x1,x2),然后用下面的公式来计算其p(x):
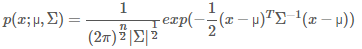
计算的时候需要带入在训练时得到的模型参数,即:由训练数据的均值向量和协方差矩阵
异常判别(决策函数)
这一步的做法有很多,可以直接做绝对值的异常判断,即,如果p(x)<ε时,就把它标记为是一个异常样本,反之,如果p(x)>=ε则不标记为异常样本。
或者做相对值的离群比较:
具体来说就是例如只采集一台机器的日志进行异常入侵检测,如果你的数据集是混合了所有的机器的全量日志,这里不能直接进行数值比较,因为它们的量纲不在同一个范畴内,可以采取的方法是比例除法的方式:
pdf_center:历史训练数据的(x1_var均值,x2_var均值)计算PDF,相当于得到钟形分布中心点的Y值
pdf_待检测样本点:当前样本点的(x1,x2)计算PDF,得到对应的Y值
pdf_center / pdf_待检测样本点:这个比例反应了这个特征维度组合的二元变量(x1,x2)在整体高斯分布上的异常离心程度。当然,整体高斯模型的形状由训练样本集的均值向量和协方差矩阵决定
4. 该用哪个模型?
| 原始模型 | 多元高斯模型 |
|---|---|
| 捕捉到这两个特征,建立一个新的特征x3x3(比如x3=x1x2x3=x1x2),去尝试手工组合并改变这个新的特征变量,从而使得算法能很好的工作。 | 自动捕捉不同特征变量之间的相关性。 |
| 运算量小(更适用于特征变量个数nn很大的情况) | 计算更复杂(Σ是n×nn×n的矩阵,这里会涉及两个n×nn×n的矩阵相乘的逻辑,计算量很大) |
| 即使训练样本数mm很小的情况下,也能工作的很好 | 必须满足m>nm>n,或者ΣΣ不可逆(奇异矩阵)。这种情况下,还可以帮助你省去为了捕捉特征值组合而手动建立额外特征变量所花费的时间。 |
5. 二元高斯分布的python实现
scipy.stats.multivariate_normal
-
A multivariate normal random variable.
The mean keyword specifies the mean. The cov keyword specifies the covariance matrix.

# -*- coding:utf-8 -*- from scipy.stats import multivariate_normal import matplotlib.pyplot as plt import numpy as np x, y = np.mgrid[-1:1:.01, -1:1:.01] pos = np.empty(x.shape + (2,)) pos[:, :, 0] = x pos[:, :, 1] = y rv = multivariate_normal([0.5, -0.2], [[2.0, 0.3], [0.3, 0.5]]) plt.contourf(x, y, rv.pdf(pos)) plt.show()

https://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.stats.multivariate_normal.html
Relevant Link:
http://studyai.site/2017/05/26/斯坦福机器学习课程%20第九周%20(3)多元高斯分布(选学)/#%E5%BC%82%E5%B8%B8%E6%A3%80%E6%B5%8B%E7%AE%97%E6%B3%95%E6%97%A0%E6%B3%95%E8%A7%A3%E5%86%B3%E7%9A%84%E9%97%AE%E9%A2%98 https://www.cnblogs.com/yan2015/p/7419972.html https://www.cnblogs.com/activeshj/p/3954213.html http://www.bubuko.com/infodetail-2275360.html http://blog.csdn.net/u012328159/article/details/51462942 https://www.cnblogs.com/gczr/p/6483762.html https://blog.datascienceheroes.com/anomaly-detection-in-r/ https://www.jisilu.cn/question/253057 http://blog.csdn.net/ironyoung/article/details/49334343
7. 基于概率统计的异常检测
基于概率统计学习的异常检测,是一种最纯粹的异常检测思想。它基于的理论依据是坚实的概率统计理论,可以这么说,概率统计模型是最能表现我们的样本数据规律的模型。但同时概率统计模型也非常依赖于训练样本的准确性以及其中概率分布的完整性。
0x1:基于概率统计模型做异常检测的基本套路
1. 设计一套特征工程框架: 概率统计模型的每个随机变量就是我们定义的特征所对应的值,特征工程的设计可以尽量融入领域经验以及先验知识,以提高特征向量的表征性 2. 对正例白样本进行数值化的特征提取和分析 3. 根据白样本的特征向量建立概率统计模型,即得到模型参数,该参数描述了概率统计模型的分布 - 这一步相当于模型train过程 4. 将线上真实样本使用同样的特征工程框架进行特征抽取,将得到特征向量输入上一步得到的模型中,根据得到的值域判定"异常程度" - 这一步相当于模型predict过程
需要注意的是,概率统计异常检测一般是针对单变量进行建模和检测的,基于多变量的概率统计函数非常难计算,计算的成本也随着随机变量的增加而急剧增加。
所以我们一般的做法是逐个针对单个随机变量进行异常概率统计。之后再基于多个单个随机变量的异常结果进行综合评分,得到一个总体的异常程度的判断。
1. 一个关于白样本的很严肃的问题
我们知道,异常检测是基于白样本进行概率统计模型建模,随后进行predict离群值计算的。但是一个很尴尬的问题的是:如何定义白样本?如何保证白样本就是白的?
在工程中,我们常常这么玩,即把历史 N 小时的数据当做是白样本,在完成模型建模之后,将当前的时刻的样本输入模型进行异常检测。
怎么做的出发点当然也没错,这是一种典型的异常基线的思维方式,但是凭什么认为历史数据就是白的呢?如果历史数据里参杂了黑的脏数据呢?
或者说如果此时此刻,历史的数据不但不是白,而且是全黑的呢?基于这样的数据拟合的概率统计模型去预测新的白样本又会得到什么呢?
2. 可用于异常概率统计的评价函数的特点
评价函数的作用是基于已知的数据集(例如白样本)进行模型拟合,得到一份模型参数,这个过程本质上可以理解为生成模型的训练过程。之后基于该已知模型输入待预测值得到的值可以用于进行异常程度的评价。
这个过程也可以被描述为一个假设检验过程,所谓假设检验,即先定义出一个假设(基于白样本拟合出一个模型分布),然后检验新的样本数据是否符合这个假设,如果不符合,则认为是异常点。
可以很容易理解,评价函数应该对数据的变化和异常(离群程度)有较强的描述和区分能力。我们在这个小节来讨论一下有哪些函数可以用于评价函数。
0x2:马尔科夫不等式
 ,其中
,其中
我们通过 的正态分布解释下,首先,
就是指的是曲线下
部分的面积:

下面的动图表现了整个马尔科夫不等式的变化趋势:

越大于平均值,概率越低。
0x3:切比雪夫不等式
 ,其中
,其中 ,
是期望,
是标准差。
还是通过 的正态分布来感受一下切比雪夫不等式:

越远离平均值,概率越低。
但是注意到切比雪夫不等式和马尔科夫不等式的一个区别是,切比雪夫不等式考虑了训练样本方差的考量因素,如果样本的方差特别大,则主要稍微偏离一些平均值,概率降低的速度会更快。
Relevant Link:
https://www.zhihu.com/question/27821324
0x4:Grubbs' Test(格拉布斯检测)
Grubbs' Test为一种假设检验的方法,常被用来检验服从正太分布的单变量数据集(univariate data set)Y 中的单个异常值。
若有异常值,则其必为数据集中的最大值或最小值。原假设与备择假设如下:
H0:数据集中没有异常值
H1:数据集中有一个异常值
1. 算法过程
Grubbs'test算法的异常点检测过程是一个迭代的过程,每轮从当前数据集中寻找出一个异常点(outlier)
1. 计算当前数据集的均值和方差。
2. 建立本轮迭代的假设:
H0:数据集中没有异常值
H1:数据集中有一个异常值
3. Grubbs' Test检验本轮的假设的所用到的检验统计量(test statistic)为 ,其中,
,其中, 为均值,s为标准差。
为均值,s为标准差。
注意到公式中使用了绝对值,所以这是一个two-tail的检验统计量,即同时检验最大值和最小值。
本轮假设是否成立的判断依据就是下式是否成立:

4. 判断迭代是否继续
当上式成立时:假设H0被拒绝,假设H1被接受,统计量对应 Yi(极大值/极小值)就是异常值,需要被剔除。提出异常值后,继续回到步骤3开始下一轮迭代。
当上式不成立时:假设H1被拒绝,假设H0被接受,则本轮没有发现任何的异常值,算法迭代结束
实际上,Grubbs' Test可理解为:检验最大值、最小值偏离均值的程度是否为异常。
5. 经过多轮的迭代后,算法停止,此时剩下的数据集就都是合乎假设检验的数据,而被筛选出来的点可以被认为是异常点
2. 使用绝对中位差代替均值 - 提高鲁棒性
在基于训练数据集计算临界值的时候,由于个别异常值会极大地拉伸均值和方差,从而导致算法未能很好地捕获到部分异常点,召回率偏低。
为了解决这个问题,采用了更具鲁棒性的中位数与绝对中位差(Median Absolute Deviation, MAD)替换公式中的均值与标准差
3. 一个典型的案例
我们对服务器的ssh/rdp/sqlserver的登录记录建立一个基本假设:在一个时间窗口内,这台服务器的来访者如果是一个正常的运维管理员,他在整个互联网上的行为轨迹应该出现出一个正态分布,而如果这个来访者是一个恶意攻击者,它的行为模式会呈现出显著的异常统计特性。

可以看到,上图中,我们明显看到,来自台湾省的这个来访IP在各个维度呈现出的行为模式基本处于整个数据集的“正态中心”位置,因此这个来访者大概率是正常的,而其他的点呈现出明显的异常特征。
grubbs test的检测结果也印证了这点:

在实践中我们发现,grubbs test的这种根据分组样本数据自适应(自动计算数据的正态均值中心)地进行异常发现,比我们之前通过人工经验硬编码一些特定的阈值进行二分类,模型的检测漏报率有显著下降。
另外一个很有趣的发现是,我们对来访者ip的4个维度分别进行grubbs test异常假设统计,在4个维度上都变现出了一致的统计异常特征,这也从侧面说明了从来访者IP的角度来说,如果其确实存在异常行为模式,则其在各个维度都会变现出异常的统计特征。
另外一个需要注意的问题是,做这种基于区间日志的异常假设统计分析,要特别注意统计的时间区间的长度,如果太短,很可能导致无法积累足够的正常行为数据,导致异常事件本身被误判为异常。
Relevant Link:
https://en.wikipedia.org/wiki/Grubbs%27_test_for_outliers https://blog.csdn.net/sunshihua12829/article/details/49047087 https://www.zhihu.com/question/280696035/answer/417665007 https://www.cnblogs.com/en-heng/p/9202654.htm
8. 序列数据的异常检测算法
0x1:序列数据的异常分类
1. 语境异常点
此种异常为序列数据中的点异常,语境异常点一定是处在序列数据的上下文中的异常点,如下图(横坐标代表时间,纵坐标代表温度)

t1处和t2处的取值是一样的,但是t2属于异常点,而t1是正常的温度。
2. 异常子序列
顾名思义,就是子序列的方式与整体序列的模式大不相同。
3. 异常序列-对比于基础序列
此种是给出一个基础的序列,判断测试序列与基础序列相比是否异常。
0x2:序列异常检测的挑战
1. 异常子序列的长度难以有效确定 2. 异常未在训练集中出现 3. 序列经常存在比较大的噪声,会产生像离群点检测一样的淹没效应(异常点和正常点的距离很小,甚至难以分别)以及掩蔽效应(异常点增多,导致其密度增大)
9. 异常检测在工程化项目中怎么用?
0x1:为什么看似很美好的异常检测算法在一些项目中不能完美work?
这个问题笔者目前为止也没有一个完美的答案,的确,学术界和工程界真的有非常多的异常检测算法。抛开场景不谈,这些算法真的是非常好,非常完美的算法,细细去品味算法的核心思想,你会惊叹于它们的合理性近乎于哲学。
但是遗憾的是,笔者在很多工程项目中写完代码后,线上的情况往往并不总能尽如人意,其中有很多的原因在于:
1. 不管是生成模型/概率统计模型/假设检测模型/无监督聚类模型,它们都需要基于一个基本假设,例如格拉斯异常检测算法的一个最基本假设是,你的数据集符合一个正态分布,而偏离正态分布均值中心的点,是异常点的概率会逐渐增大。 但是,在安全攻防领域(笔者是做安全攻防工作的),很多时候,我们面对的是海量的用户业务日志以及黑客入侵日志,很多时候,这种假设不一定100%能成立,比如一个黑客入侵也可能产生大量密集的异常事件,这些事件可能从统计上并不能呈现出明显的tail-side abnormal现象,当然这也涉及到你的统计时间窗口怎么设计的问题。 2. 异常检测,尤其是概率统计/假设检验类的异常检测,是一个纯数学上的概率计算问题。而安全入侵检测是一个物理世界的现实问题。物理问题可以通过数字向量来抽象吗?这个问题非常关键,答案应该是不能的,至少不能100%完美的代表,很多时候,我们根据我们自己的一些领域先验知识进行的特征工程,这个过程已经包含了一些信息丢失了,在一份存在信息损失的向量上进行算法检测,得到的结果的准确性也自然会下降。
0x2:结合一些领域知识来缩小假设类的范围
我们知道,在PAC可学习理论中,一个很重要的概念是,待搜索的假设类的越被限制,估计风险就会减小,但同时估计风险会升高。但是总体来说,得到的最终模型效果会提高。
缩小假设类的方法有很多,例如正则化惩罚、提前剪枝等等。
但是一个最重要的方法是通过引入领域先验知识,来直接对假设类进行缩小。换句通俗的话来说:
如果你对的业务场景已经知道了一个非常强的先验知识,一个好的做法是直接将其hard coding为一个规则,而最好不要通过特征向量的方法表征后输入算法模型,“期望”算法模型去“学习”你的这种经验,这可能会导致欠拟合问题。
Copyright (c) 2018 LittleHann All rights reserved


 浙公网安备 33010602011771号
浙公网安备 33010602011771号