南京大学 静态软件分析（static program analyzes）-- CFL-Reachability and IFDS 学习笔记

一、Feasible and Realizable Paths

IFDS是一种分析框架，在这种框架下，分析的数据流是满足CFL-Reachability这一性质的。

Infeasible Paths

实际分析时，JDK中一个方法能产生的CFG是非常复杂的。不过，并非所有的路径都会被执行到，一个很自然的想法是，只分析可能被执行的路径。

所谓Infeasible Paths，指CFG中实际执行不到的路径。静态分析不能肯定地判定路径是否可达。

虽然并非所有的路径都会被执行到。可是判断一条路径是否feasible本身是不可判定(undecidable)的。但这并不代表我们束手无策了，我们来看一个例子：

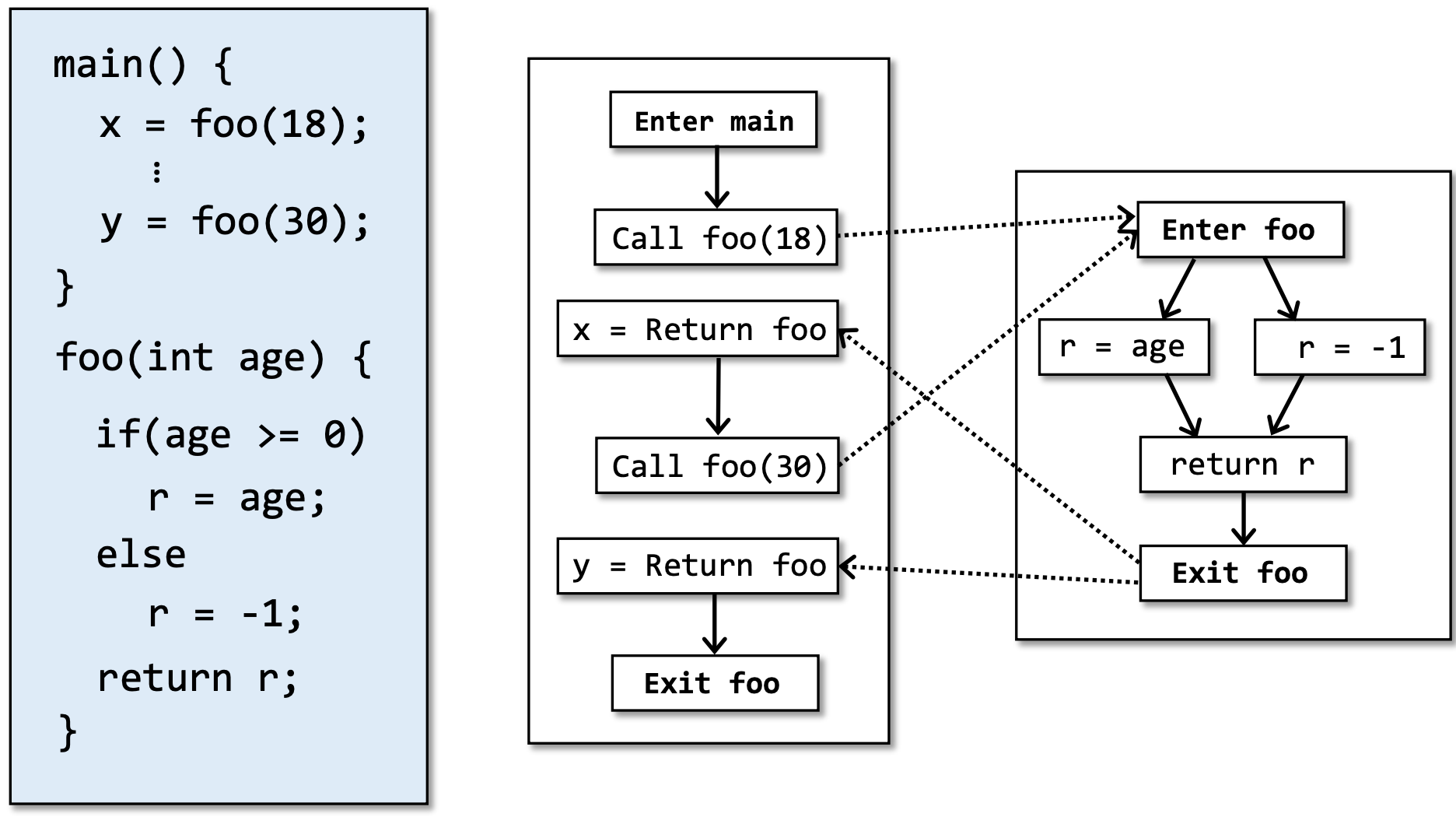
动态执行时x和y都有确定的值，而上下文不敏感的分析中，x和y的取值是不确定的，更具体的说，就是{18,30,-1}。

仔细地观察x的两个不精确的分析结果，可以发现-1这个结果在当前框架下是不可避免的：

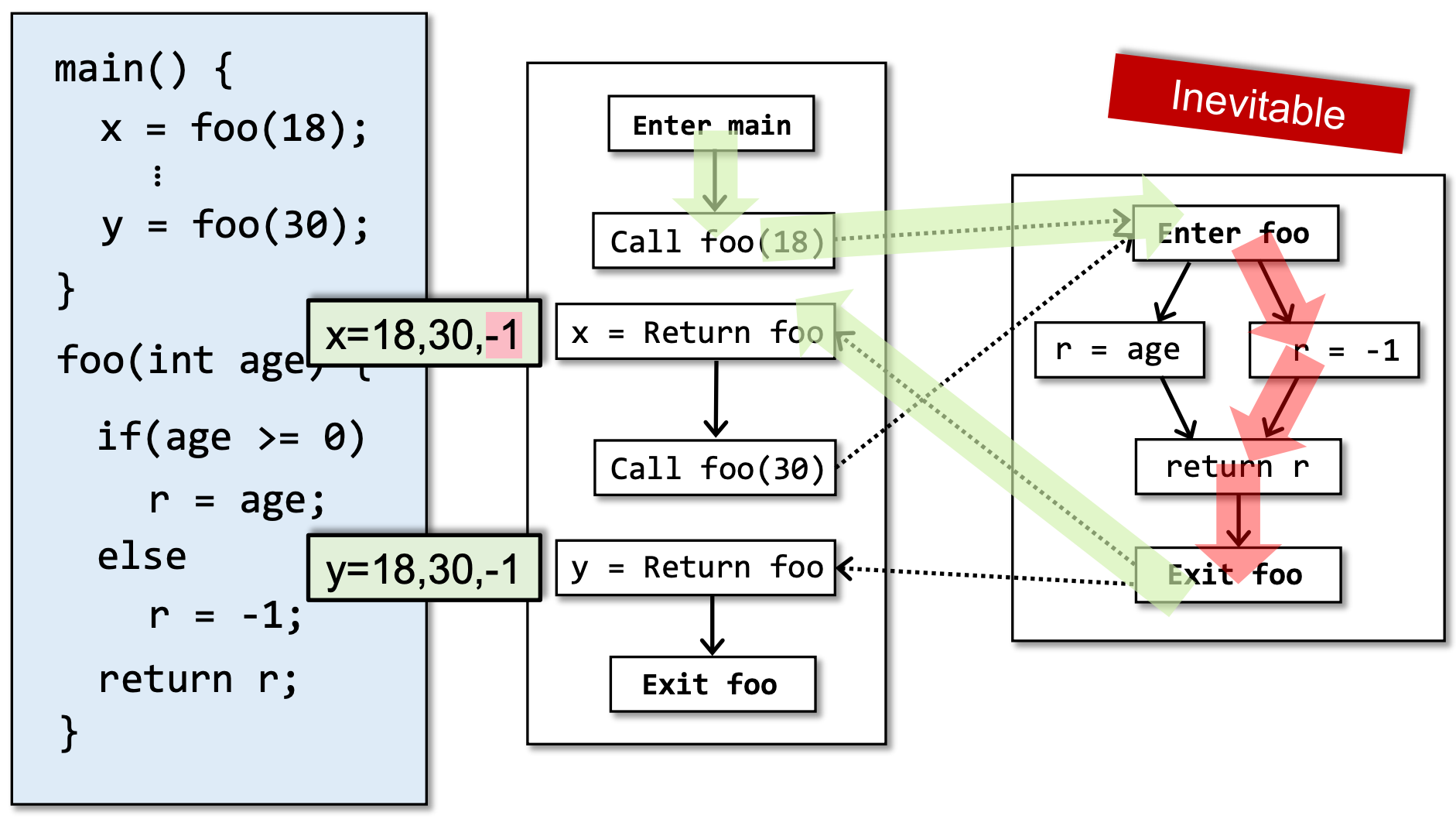
而30这个不精确的结果则是可以避免的（比如使用我们之前介绍过的上下文敏感指针分析）：

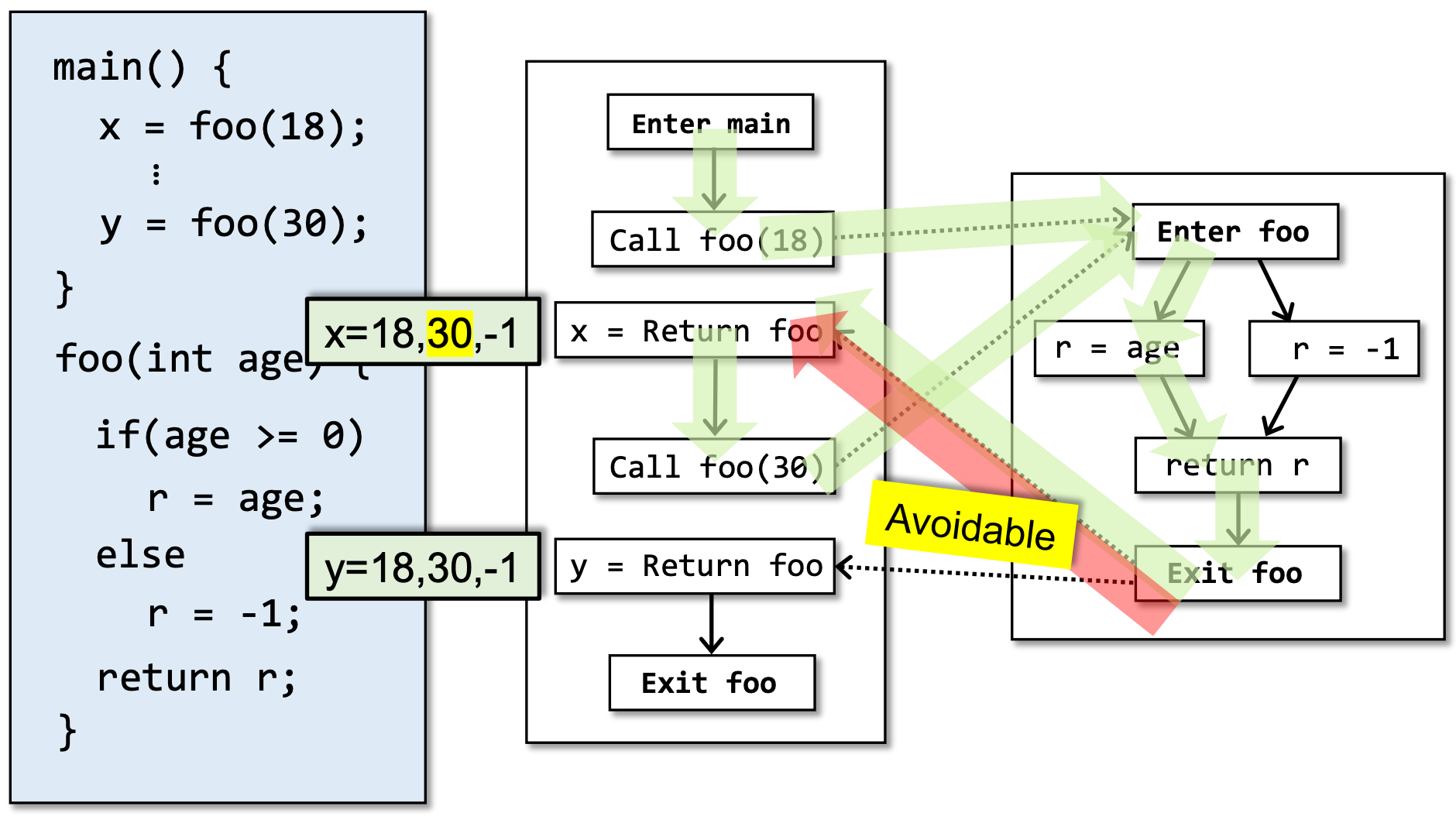
Realizable Paths

• Realizable paths may not be executable, but unrealizable paths must not be executable.
  • 可以把executable/feasible path看作realizable path的真子集
• Our goal is to recognize realizable paths so that we could avoid polluting analysis results along unrealizable paths.
  • 这个问题和括号匹配问题本质上是一样的。
  • 使用上下文无关文法能够很好地识别一个匹配的括号串(Balanced-Parenthesis Problem)。

 

二、CFL-Reachability

定义

• CFL-Reachablity：在普通的CFG可达条件下，同时路径上的label拼接起来满足context-free language定义的一个word，此时该路径是CFL-Reachable的。
• context-free language（CFL）：由CFG产生的语言。
• Context-Free Grammar (CFG)：CFG是一个形式化的语法，满足上下文无关文法。

CFL-Reachablity相关例子：部分括号匹配问题（Partially Balanced-Parenthesis） 

部分括号匹配问题（Partially Balanced-Parenthesis）：有 )i 右括号一定要有对应的 (i 左括号，反之有 (i 不一定要有 )i，因为在分析过程中，可能还没有分析到对应的右括号的，但此时也可能是Realizable的

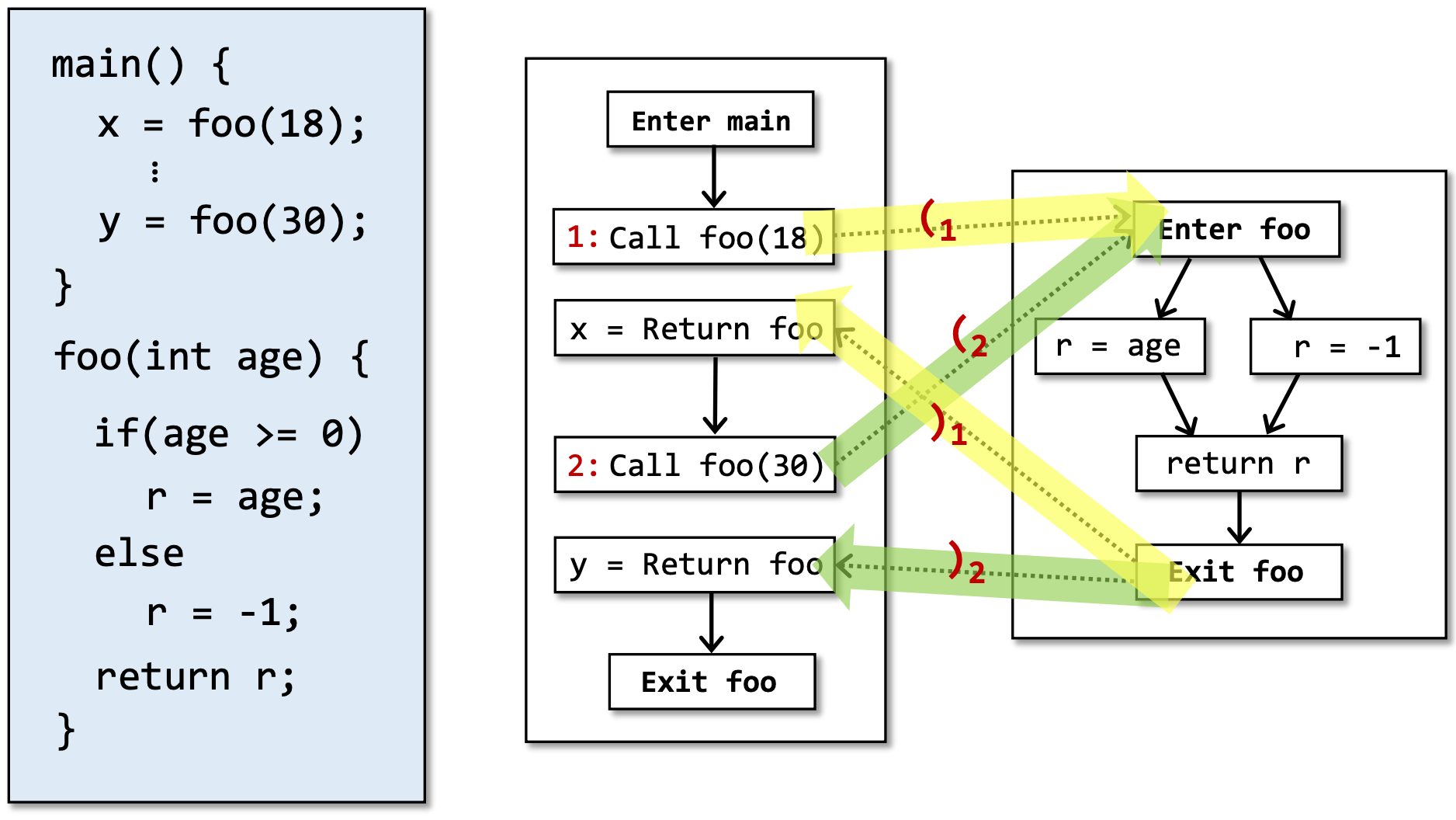
我们进一步定义一个语言L(realizable)，右侧黄色框中的4个字符串都是语言L的一部分。 

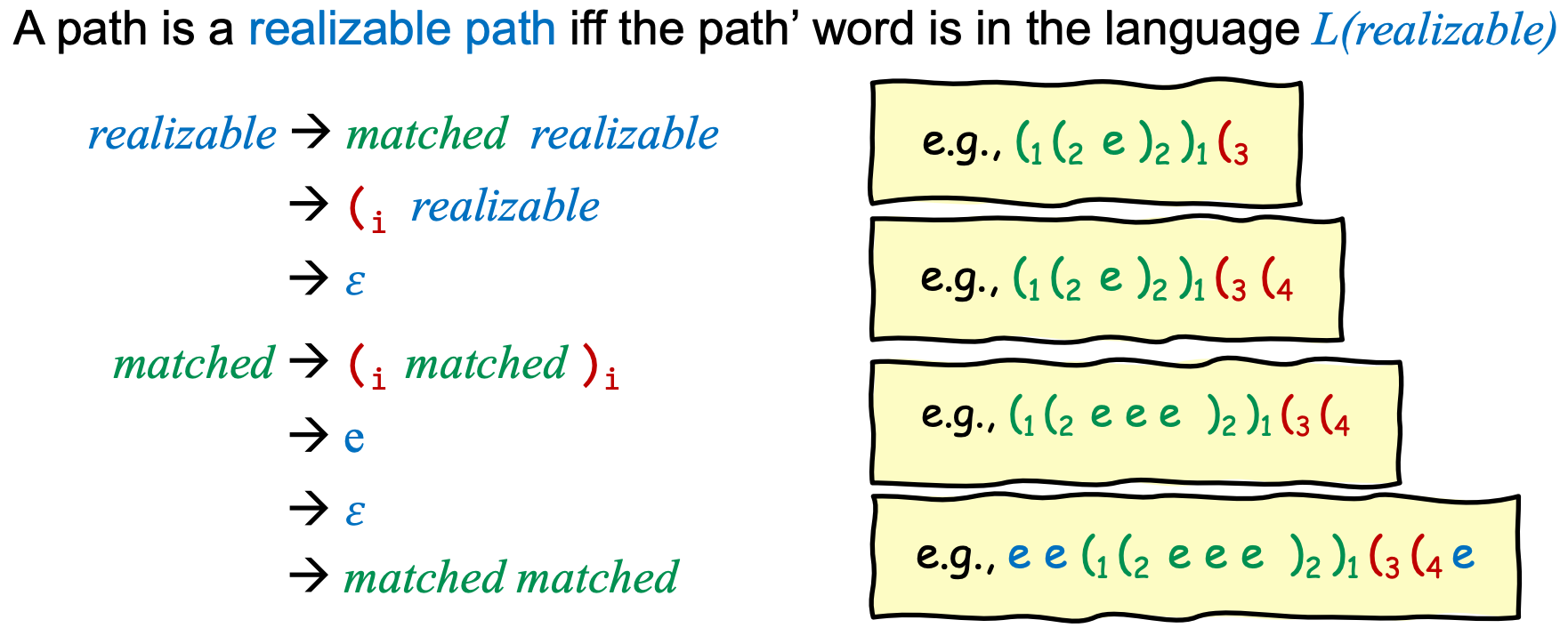
我们用前面的例子来进一步说明语言L(realizable)，

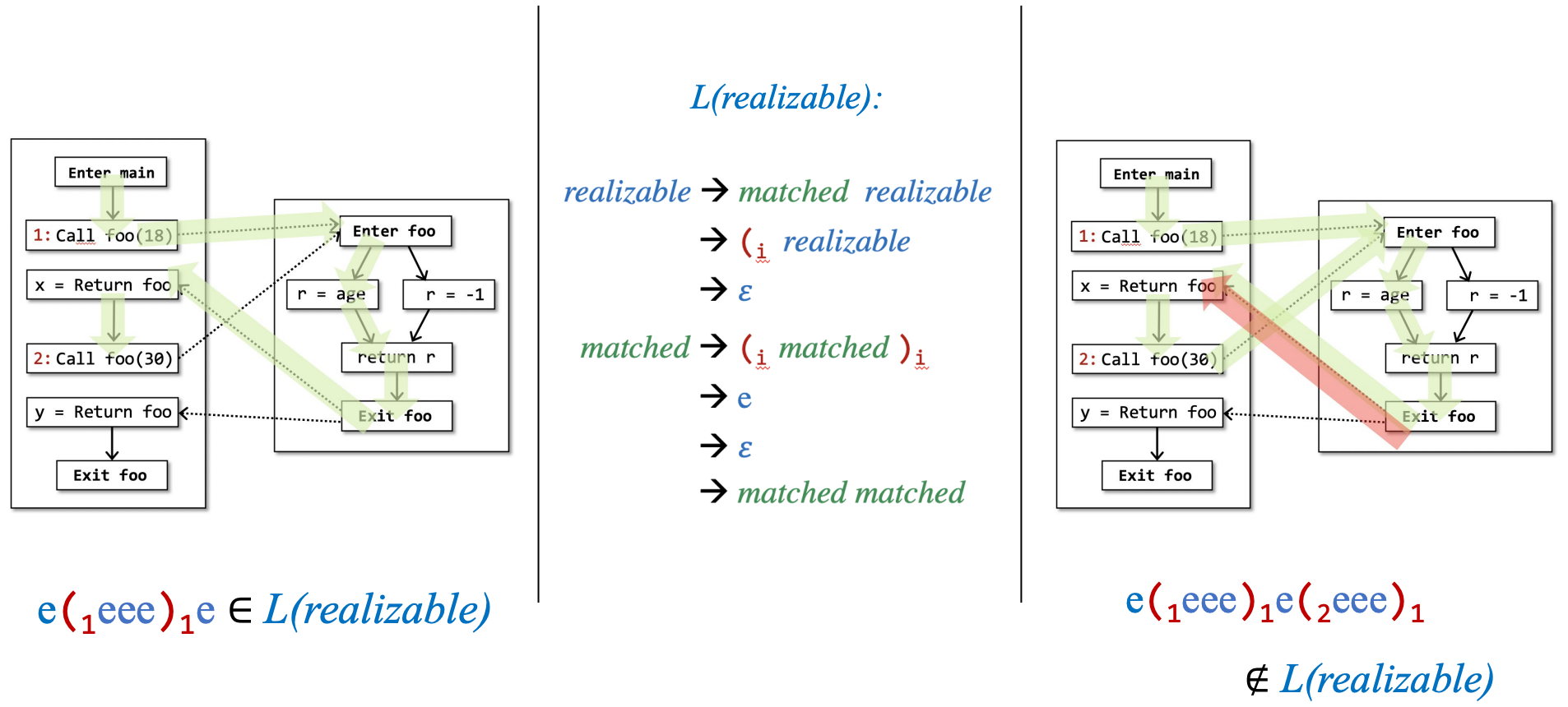
• 左边的绿色path，根据中间定义好的realizable语法，是满足的，所以是realizable的。
• 右边的红色path不满足语法，是unrealizable的。

e表示一条边，括号表示方法调用的label。path上一系列的label满足我们定义好的CFL语法，则能判断它是realizable的。

 

三、Overview of IFDS(Interprocedural, Finite, Distributive, Subset Problem)

• IFDS：把程序分析问题转化为图可达性问题。
• IFDS(Interprocedural，Finite，Distributive，Subset Problem)：
  • Interprocedural：全程序分析
  • Finite：有限域下的分析
  • Distributive：重点，决定了一个问题是不是能够用IFDS来解决。Transfer Function满足分配律：f(a  b)=f(a)  f(b)
  • Subset：集合问题（比较容易理解，很多程序分析都是集合问题）

Recall For "Path Function" and "Meet-Over-All-Paths(MOP)"

所谓”Path Function“，可以理解为按照顺序，先后应用一条path上edge/node的transfer function：

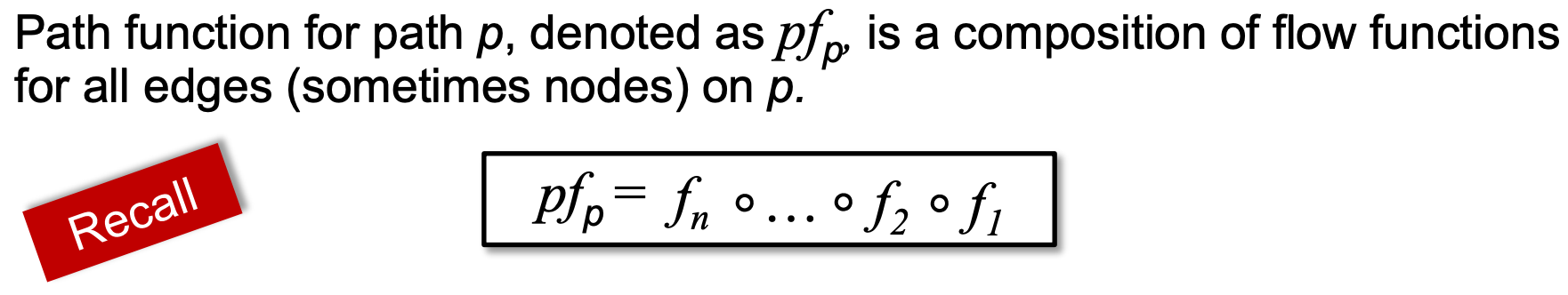
所谓”Meet-Over-All-Paths(MOP)“，即对所有的开始点start，都以bottom作为path function的输入，并在终点n处对所有的结果做meet操作。

Meet-Over-All-Realizable-Paths (MRP) 

所谓”Meet-Over-All-Realizable-Paths (MRP) “，即在前者概念的基础上限制Meet的对象为Realizable-Path 

Overview of IFDS 

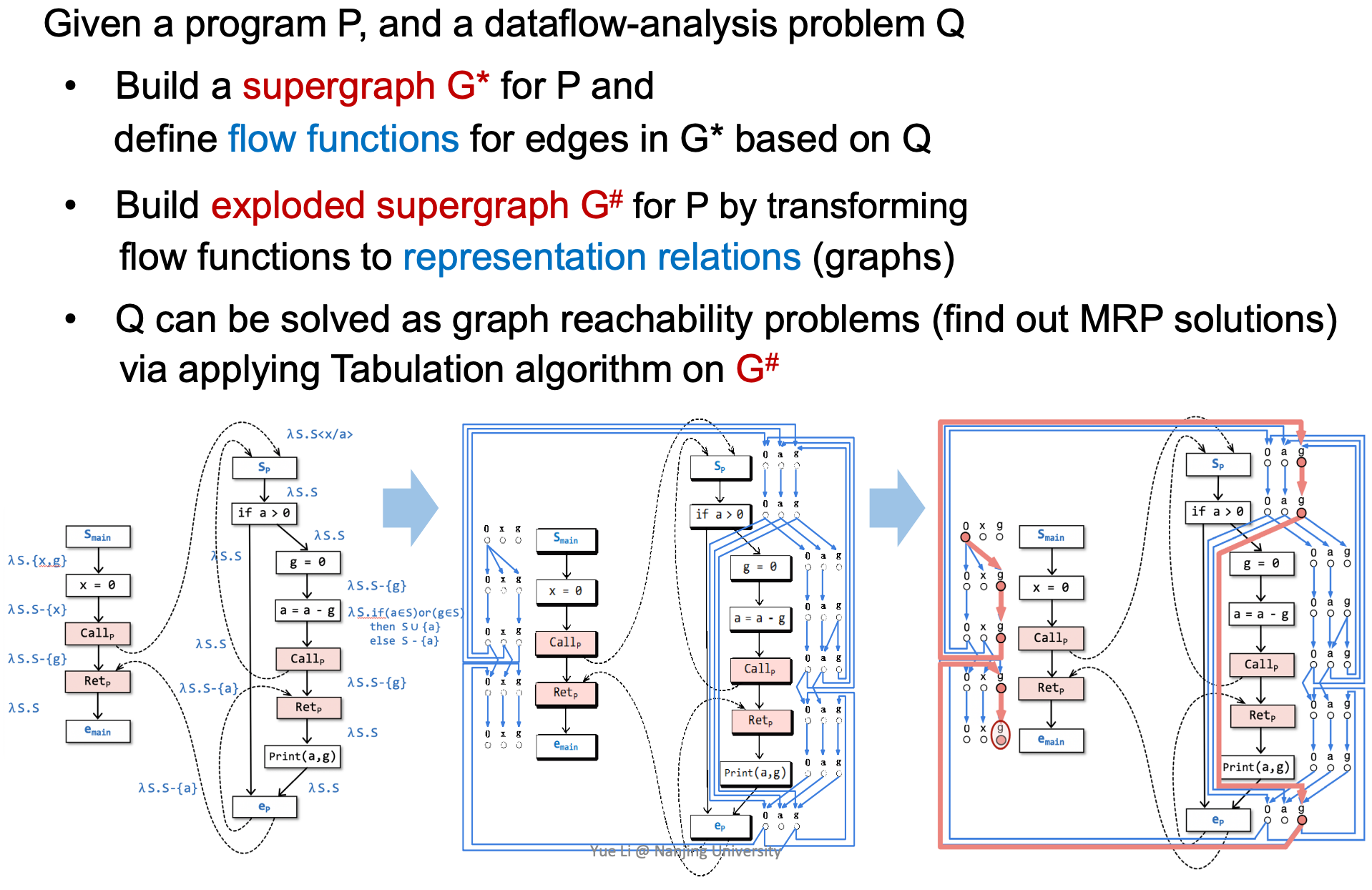
IFDS概要：给定一个程序P和一个数据流分析问题Q：

• 构造一个P的supergraph G*，根据Q定义G*上的边的流函数。
• 通过将定义的流函数应用于关系表达（图），构造P的exploded supergraph G#（分解为子图）。
• Q能够通过在G#上应用Tabulation算法来转化为图可达问题（通过解决MRP问题）来解决。对于程序中的一点n，如果存在一条realizable的，从<Smain, 0>到<n, d>的path，则有data fact：d∈MRP_n。

 

四、Supergraph and Flow Functions

Supergraph

可以理解成IFDS分析体系下的ICFG(Interprocedural Control Flow Graph，即过程间控制流图)。

在IFDS中，整个程序被一个Supergraph G*=(N*, E*)表示，G*包含所有的流图G1, G2, ... （每个函数对应一个流图）

• 每个流图中添加了辅助的开始节点s和退出节点e
• 每个函数调用包含调用节点Callp和返回节点Retp

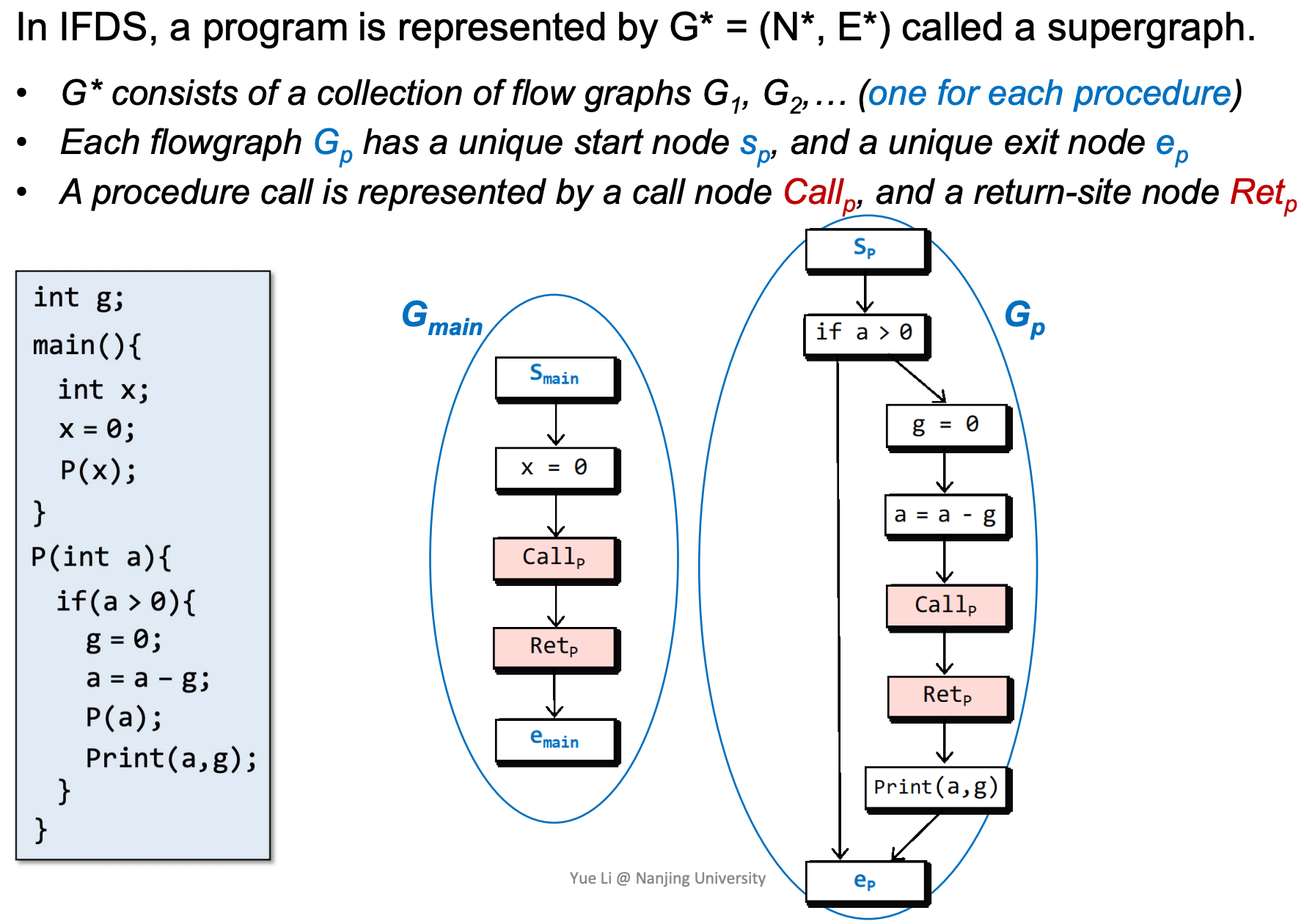
G*有三种edge（图中的G*即指supergraph）：

• An intraprocedural call-to-return-site edge from Call_p to Ret_p
• An interprocedural call-to-start edge from Call_p to s_p of the called procedure
• An interprocedural exit-to-return-site edge from e_p of the called procedure to Ret_p

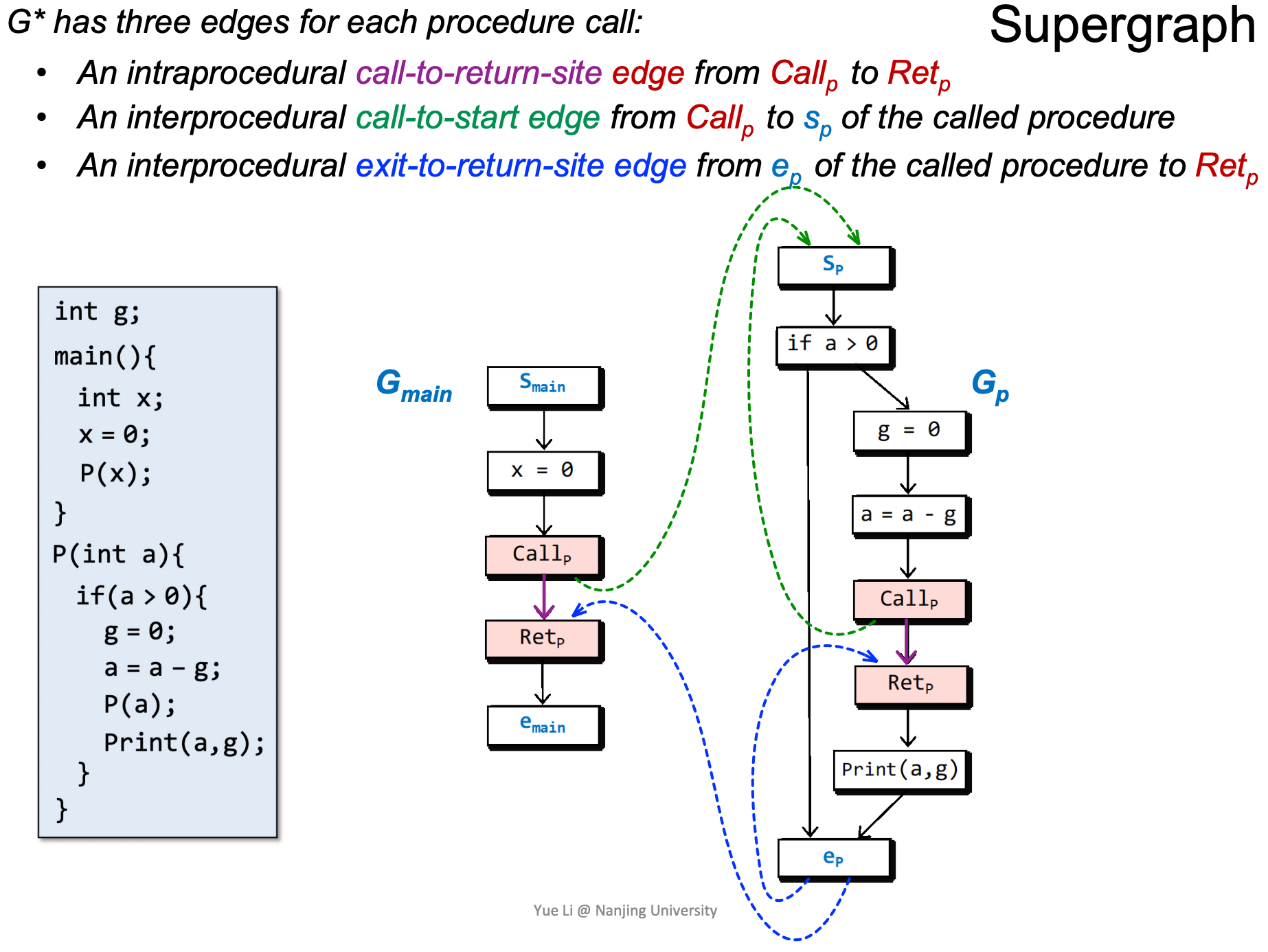
Flow Functions

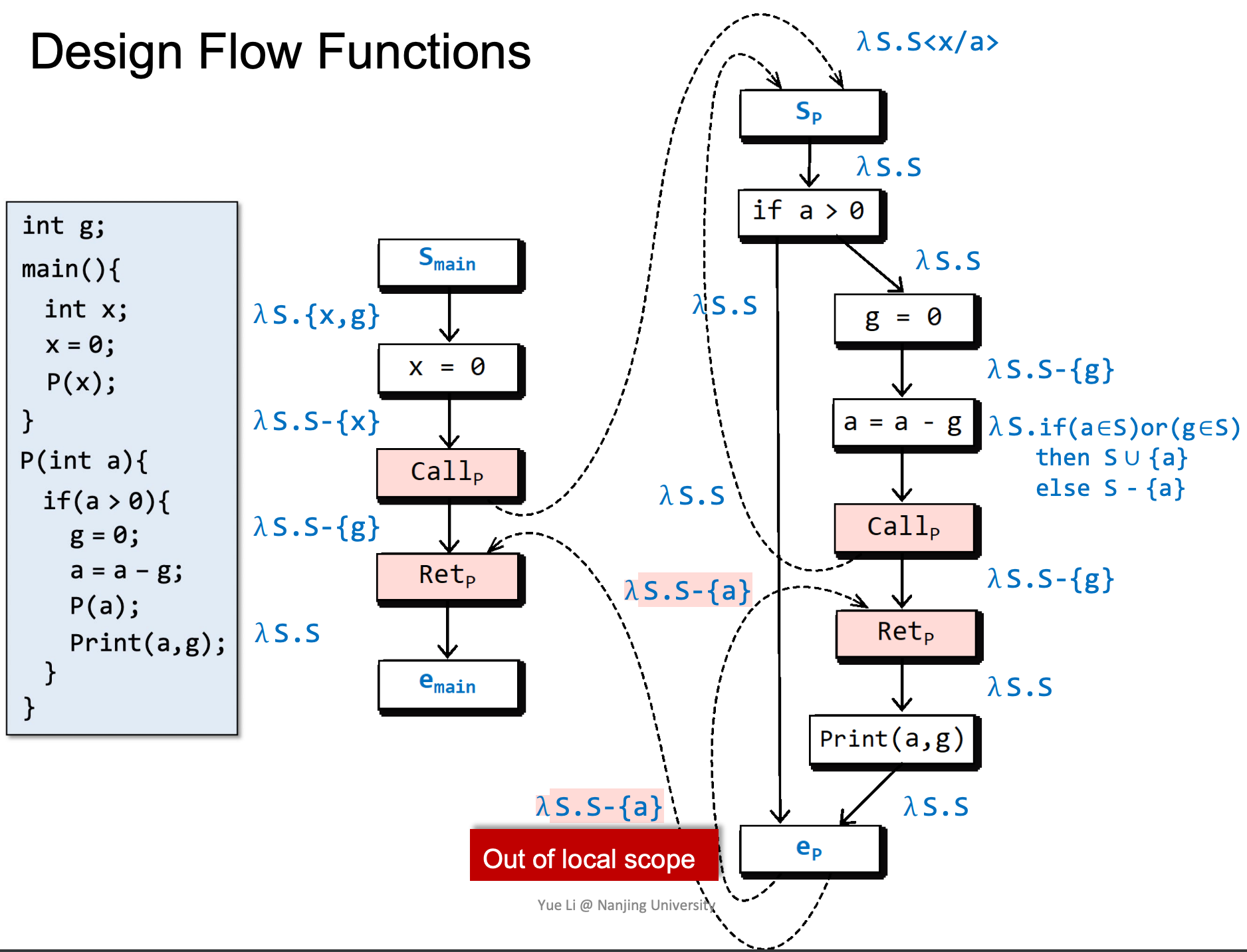
我们用一个例子来分析FLow Functions，这个例子是：可能未初始化的变量的分析：分析出在程序点n处可能未被初始化的变量。

1、lambda expression

以 λ 标识一个lambda表达式：

• 从开头到中间点间的符号代表参数列表
• 从中间点到最后的符号代表函数体
  

如下例子，就代表这样一个函数调用： 

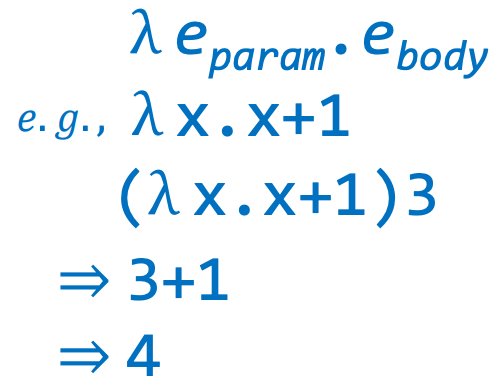
• 函数以x作为输入参数
• 函数返回值为x+1
• 调用函数时传入的参数为3

2、Example of Flow Functions 

在进入main后，全局变量g和局部变量x一定是没有初始化的。 

 

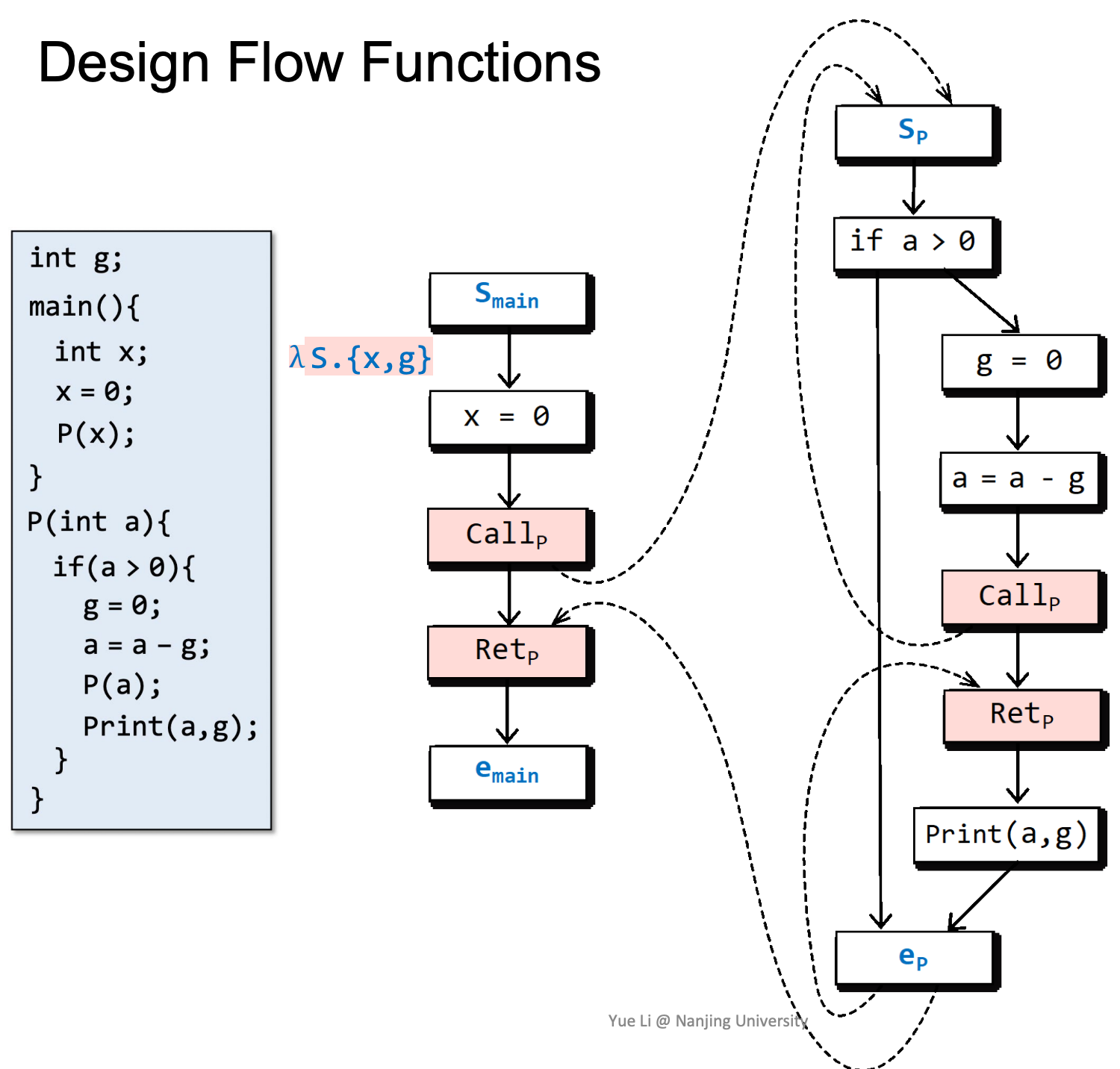
随后x被初始化：

 

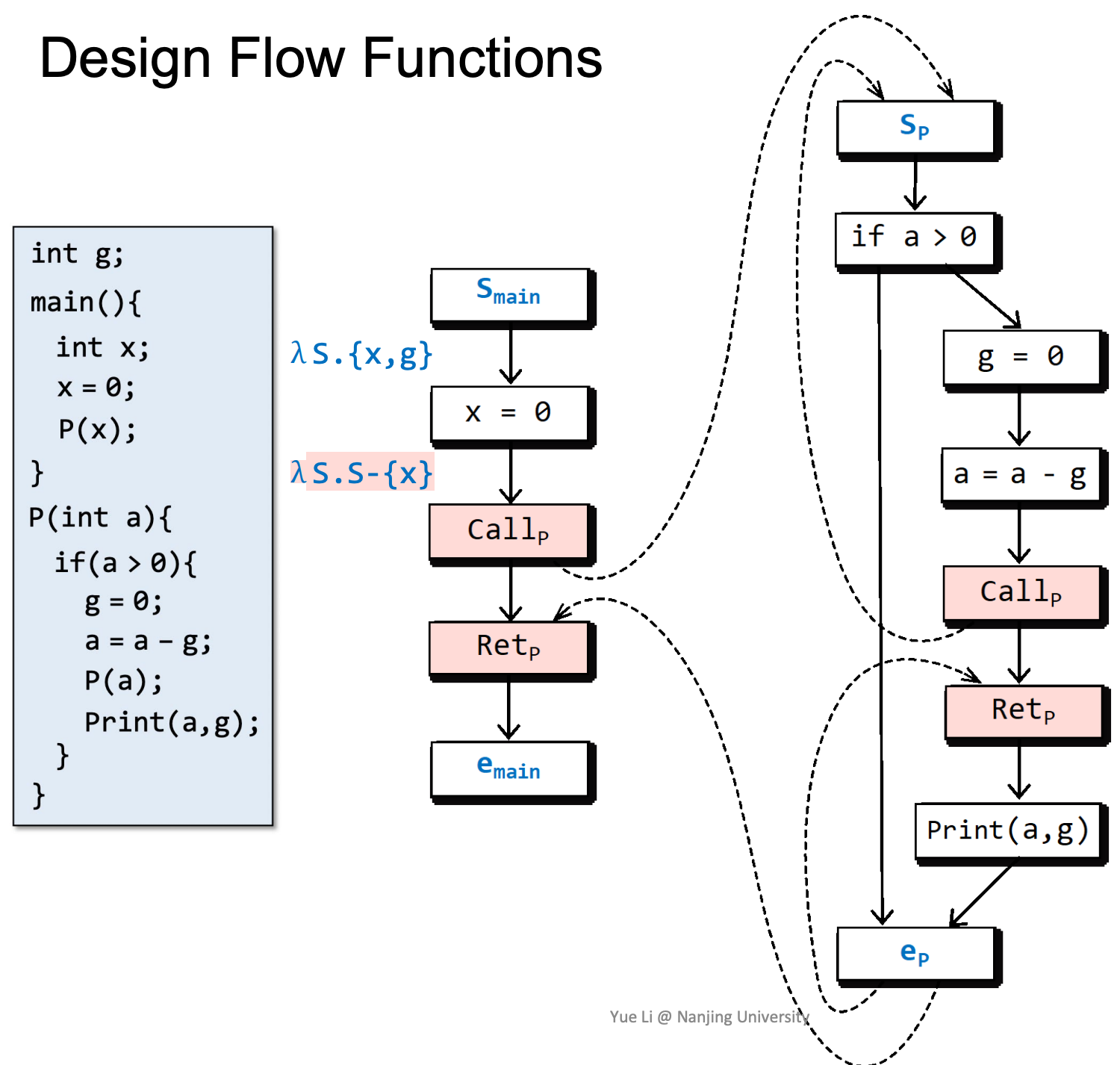
以x来初始化a，a是否被初始化与x一致。 

 

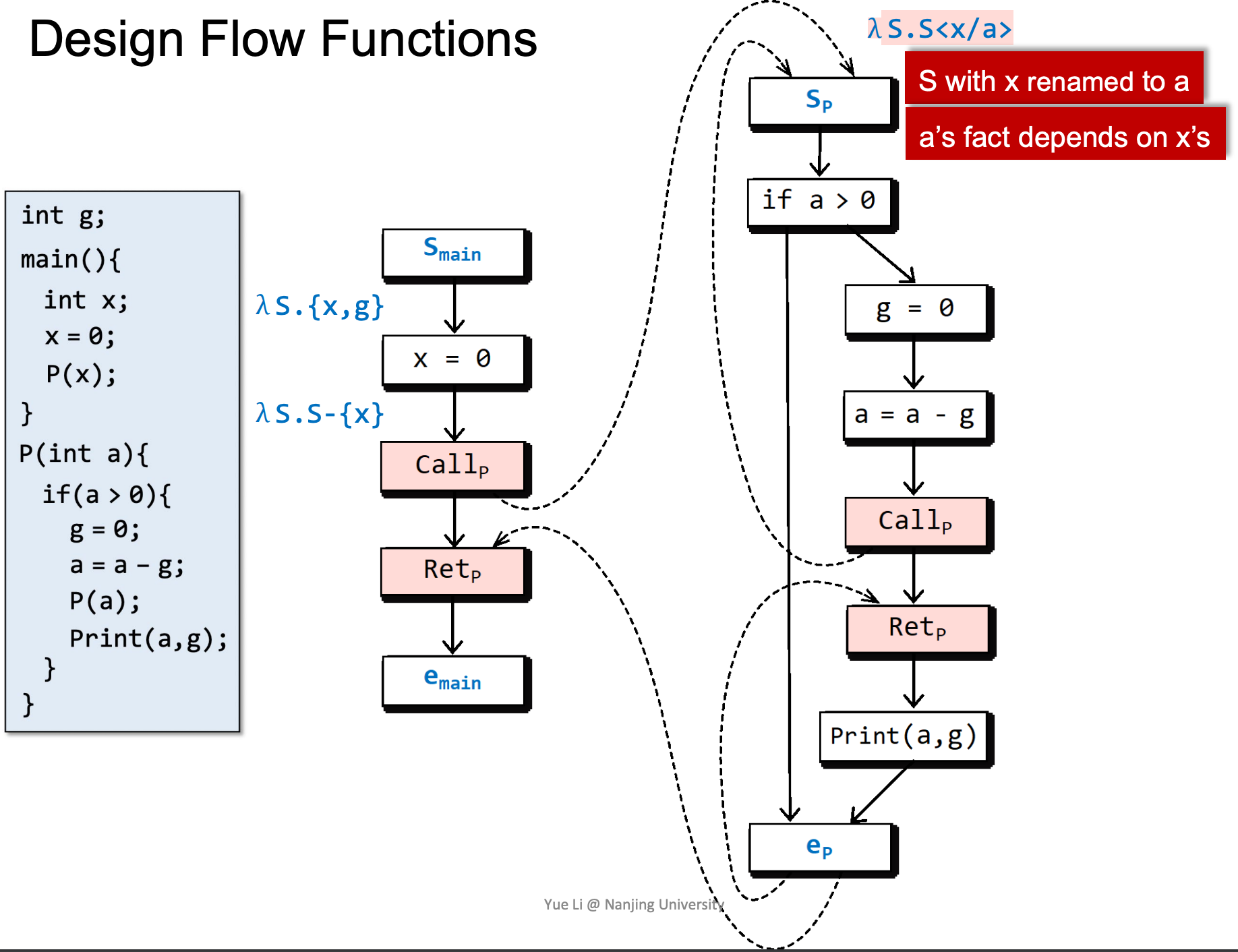
如果a和g都被初始化了，则a是被初始化的，否则认为a没有被初始化。 

 

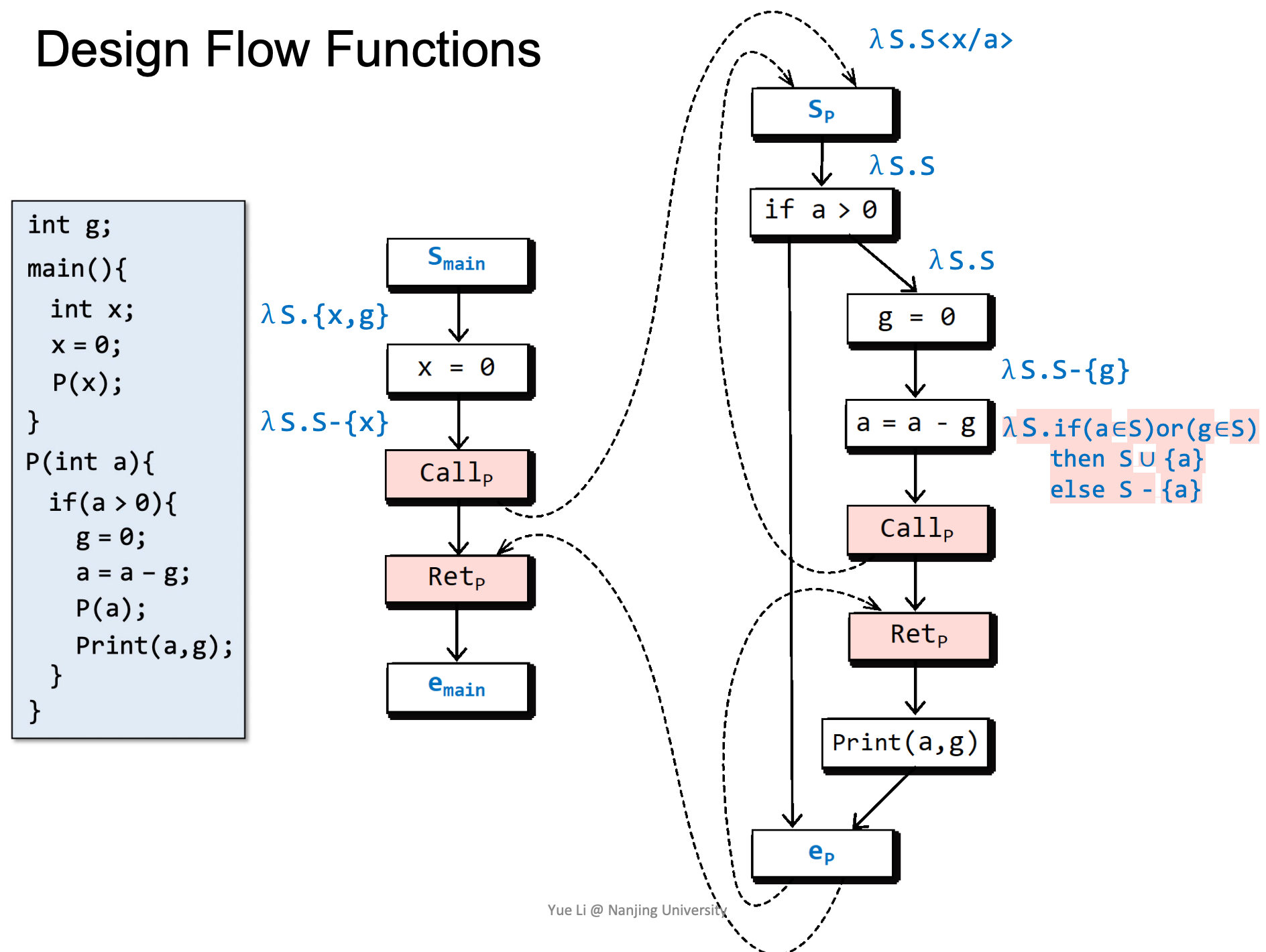
注意左侧以红色标记的函数，这样写能够使得在Ret_p处g是否已经被赋值/初始化取决于是否在被调用函数中被赋值。

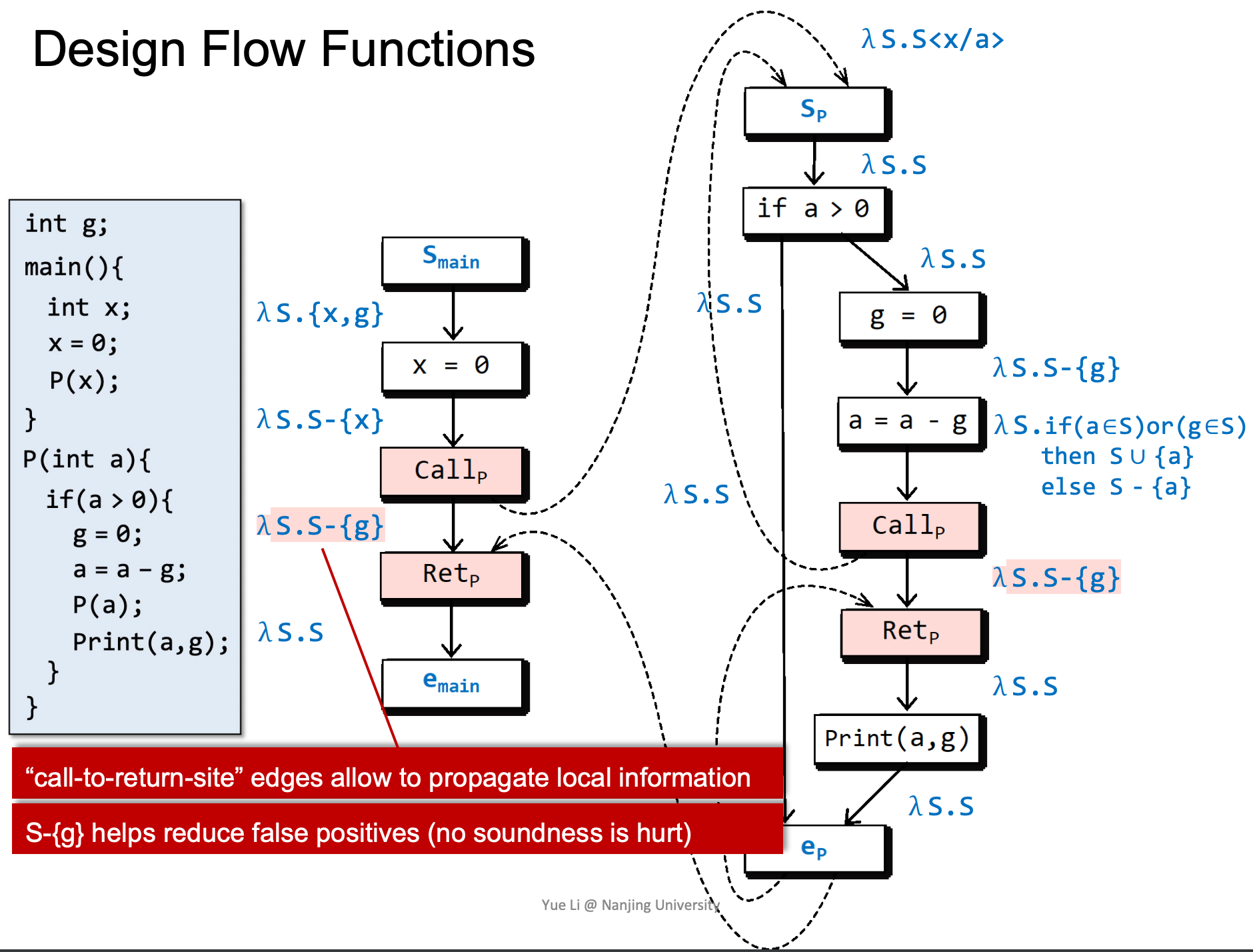
这里涉及一个特殊的情况，由于离开了函数，所以要去除函数内部变量a。

 

  

五、Exploded Supergraph and Tabulation Algorithm

Build Exploded Supergraph

• 通过将定义的流函数应用于关系表达（图），构造P的exploded supergraph G#（分解为子图）；
• 每个流函数可以表示为有2(D+1)个节点（上面D+1个,下面也是D+1个），最多(D+1)^2条边的图（上面乘下面，二分图），D表示dataflow facts元素个数（如待分析的变量个数）。上半部分表示输入，下半部分表示输出。边代表某个状态的输入是否会影响另一个状态的输出。

构造子图时遵循如下3种规则：

1. 0 → 0；无条件地在图中加一条0到0的边
2. 0 → d1，y inf(Ø)；对于一个没有输入但有输出的转化函数，加上相应的边（0到xxx）
3. d1 → d2 对于一个既有输入也有输出的函数，加上相应的边

举一个例子，

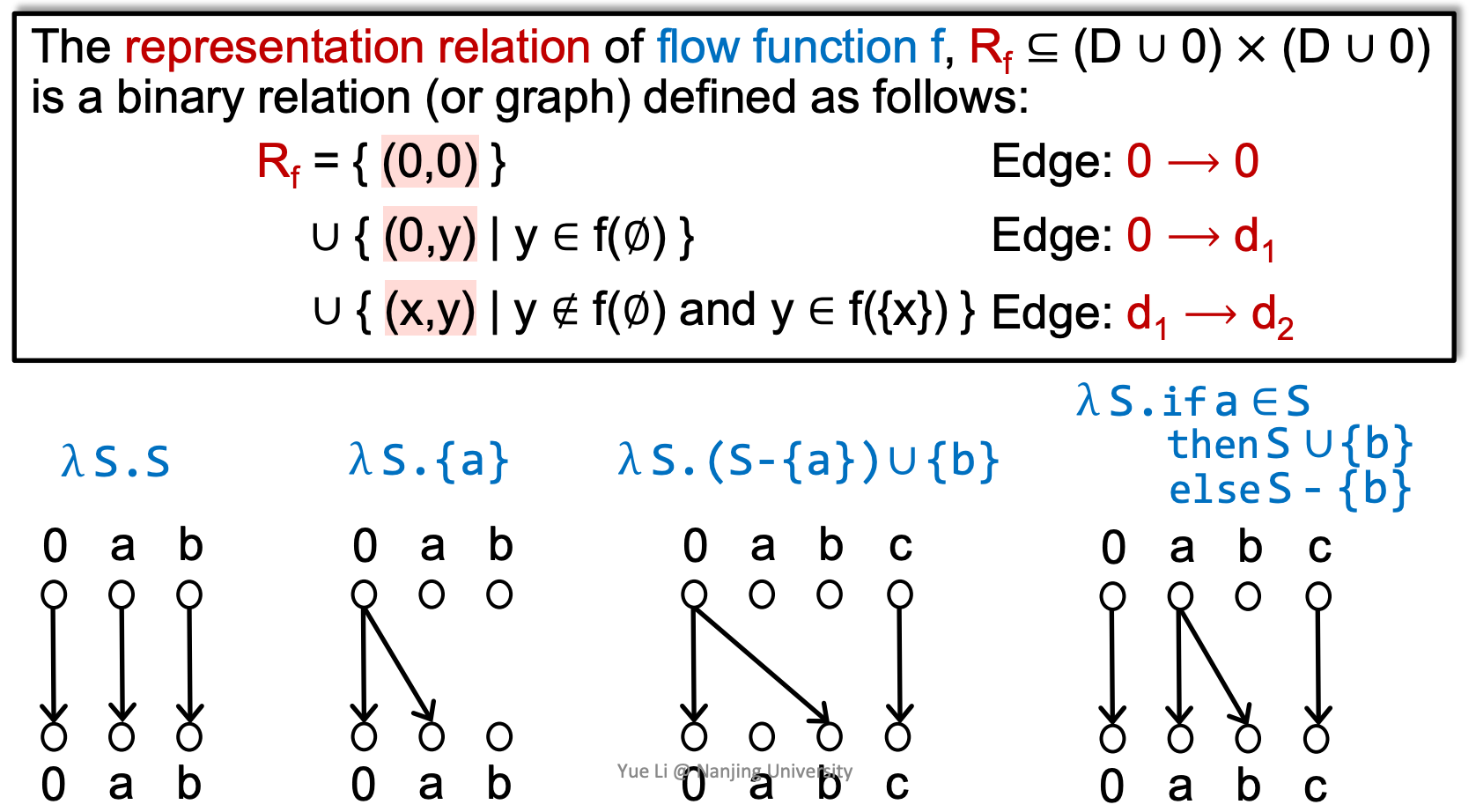
理解时，枚举上、下半图的每对节点，考虑输入这些值时对于对应的输出满足哪些规则（比如考虑a初始化和a未初始化），并连上相应的边。特别地，如果输入对输出没有影响，则判断为f(Ø)，被0连接的下部图节点会取消其他上部图节点的连接（相当于为f(Ø)）。

• 第一个转化函数，输入什么输出什么，所以直接连上对应的即可。
• 第二个转化函数，需要注意lambda虽然有“输入”S，但S可以为空，并且输入空也返回a的状态，所以只满足规则1、2。
• 第三个转化函数，会无条件传递b的状态，所以0除了连0还连接了b；输入b的初始化状态，不影响a、b、c的初始化结果；此外，输入c的状态就输出c的状态，所以c连c。
• 第四个转化函数，如果输入包含a，则输出一定包含b；否则一定不包含b

为什么一定要0节点：0节点代表了空输入，如果没有0节点，有空输入但有输出的情况就不能通过exploded supergraph表示出来，造成漏报。0 → 0又称为Glue Edge（胶水边）

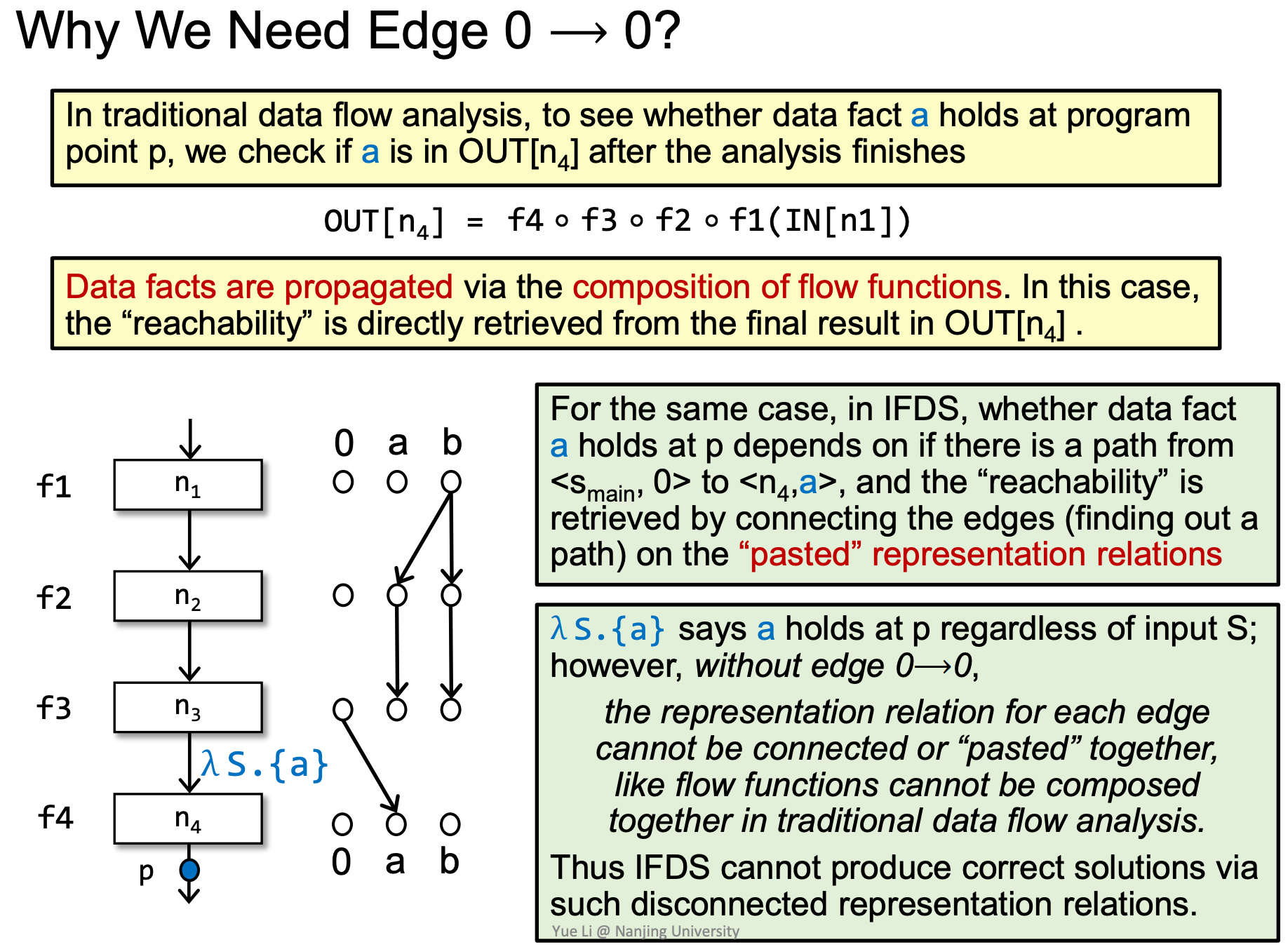
加上这条总是存在的Glue Edge之后，就可以满足IFDS分析的要求。

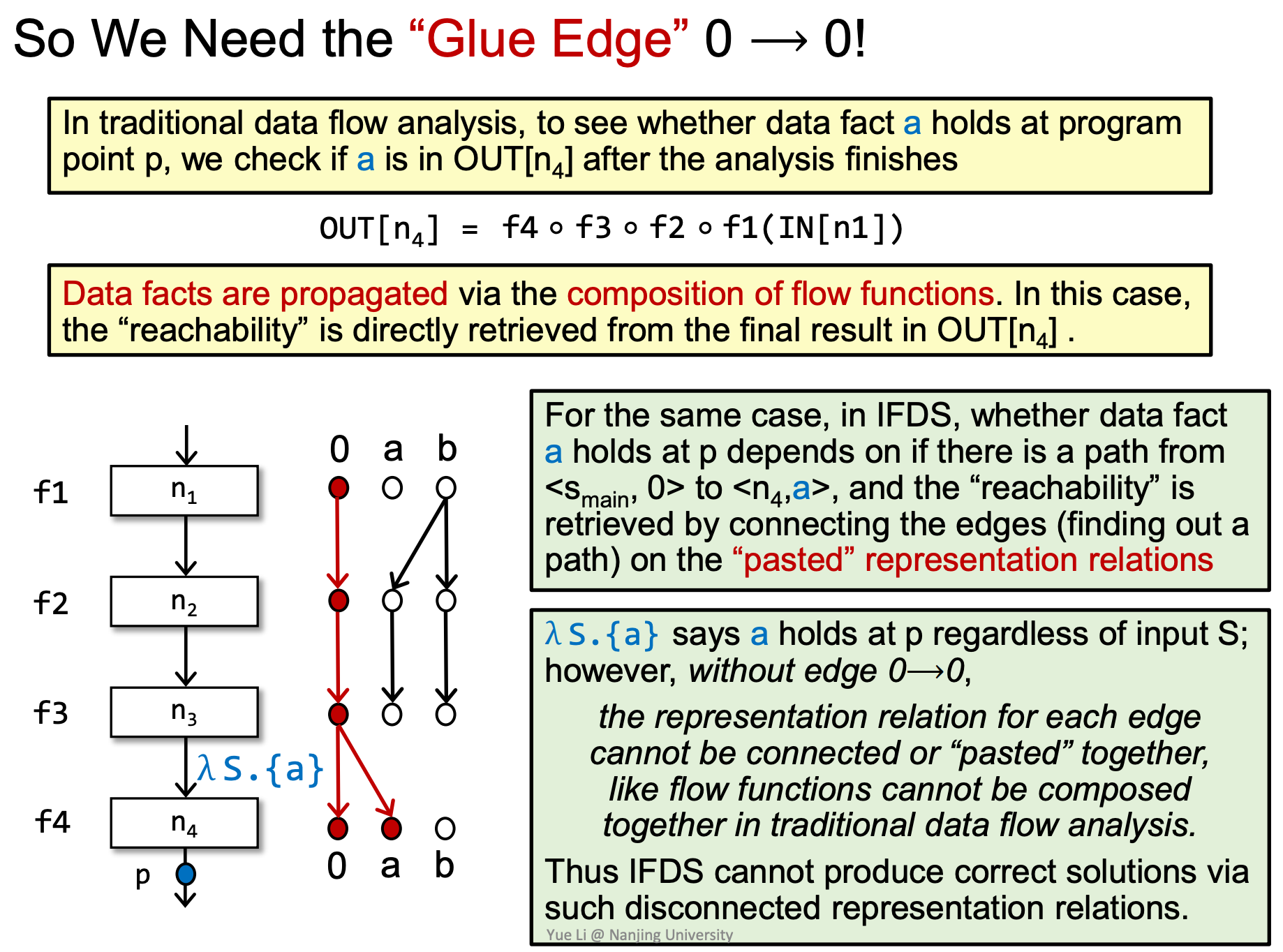
构造完成所有的边的子图后，我们将一条路径上的所有子图按顺序连接起来，即可通过可达性来判断某个变量是否被初始化了。

构造子图的实例

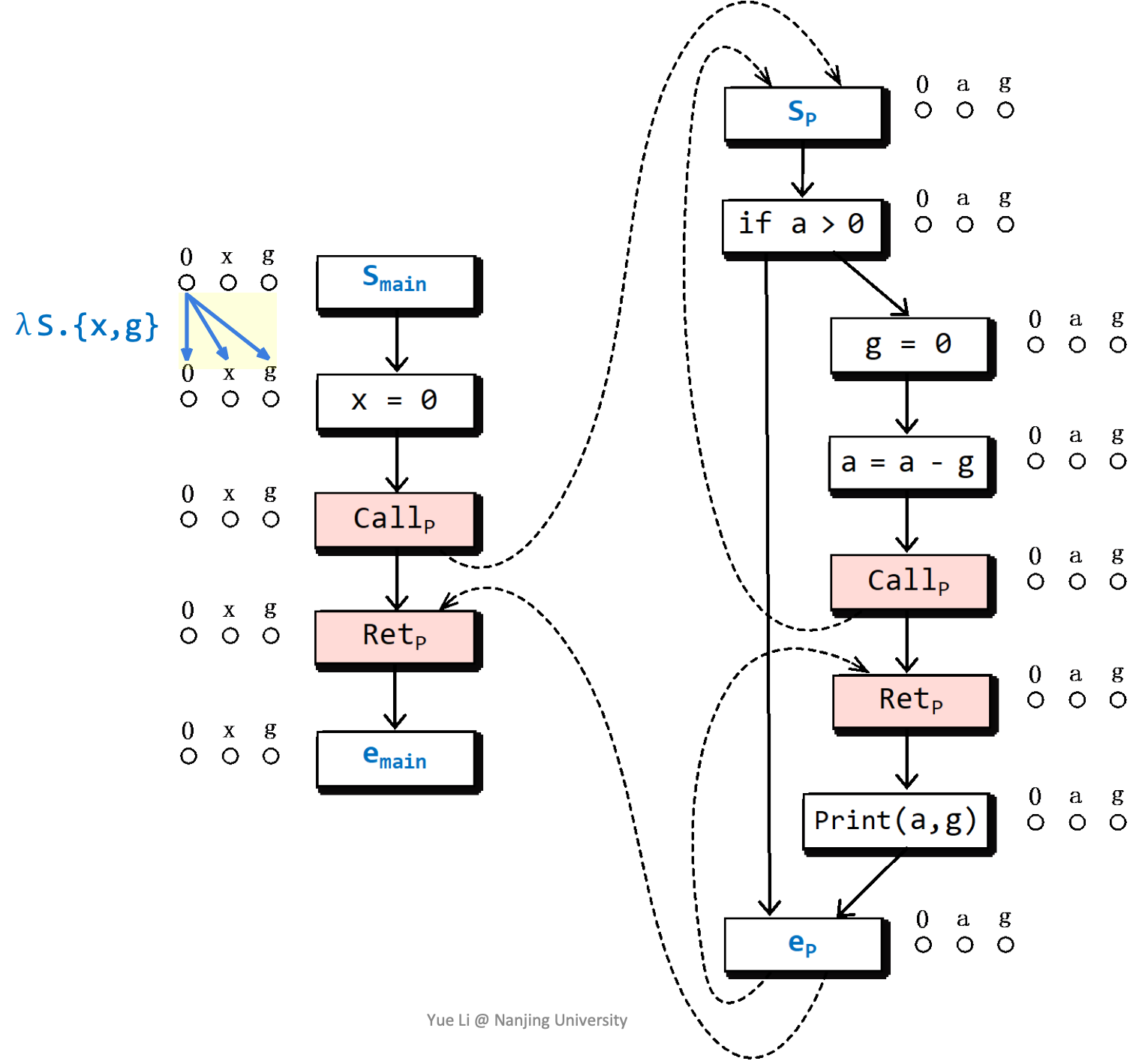
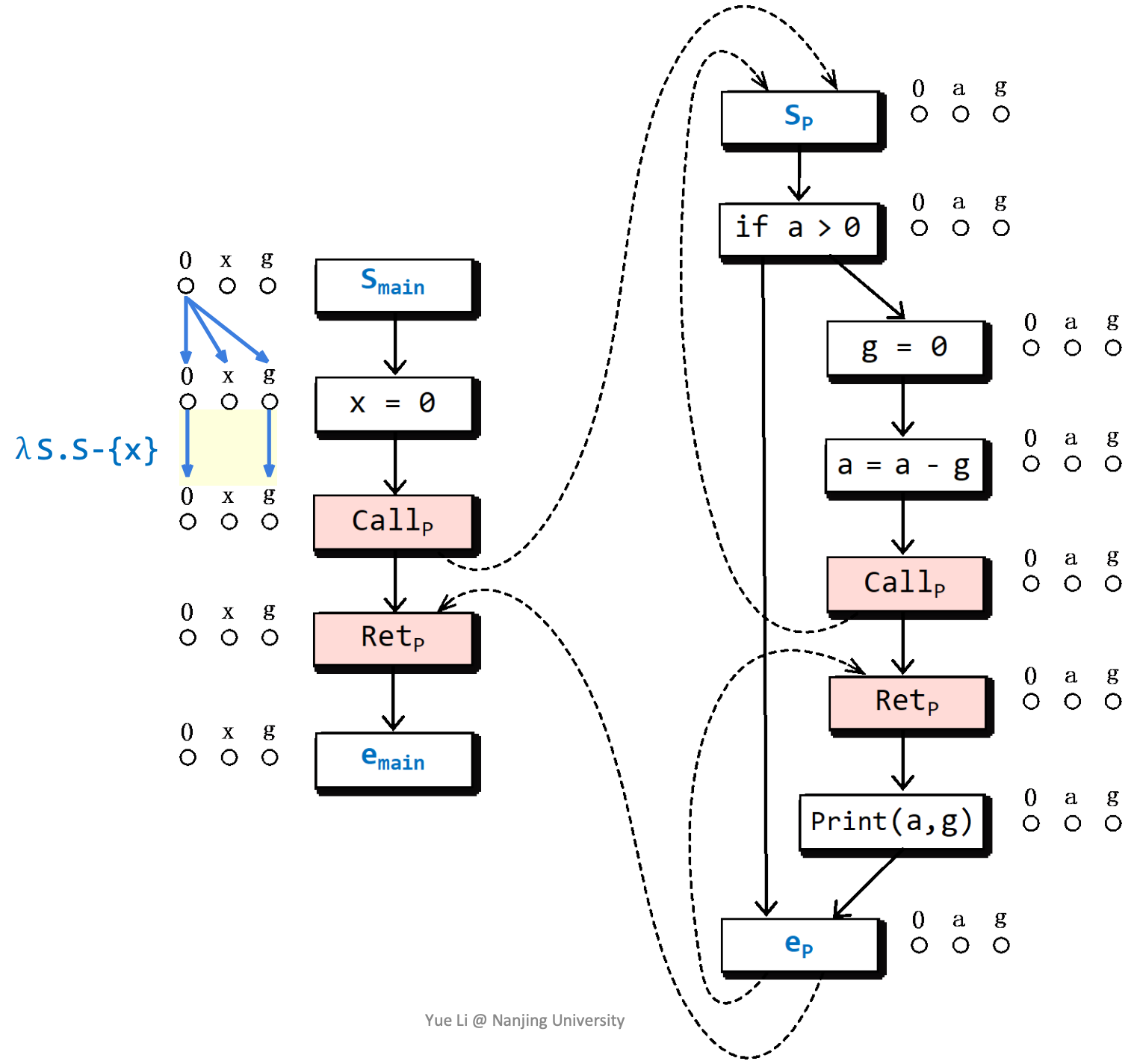
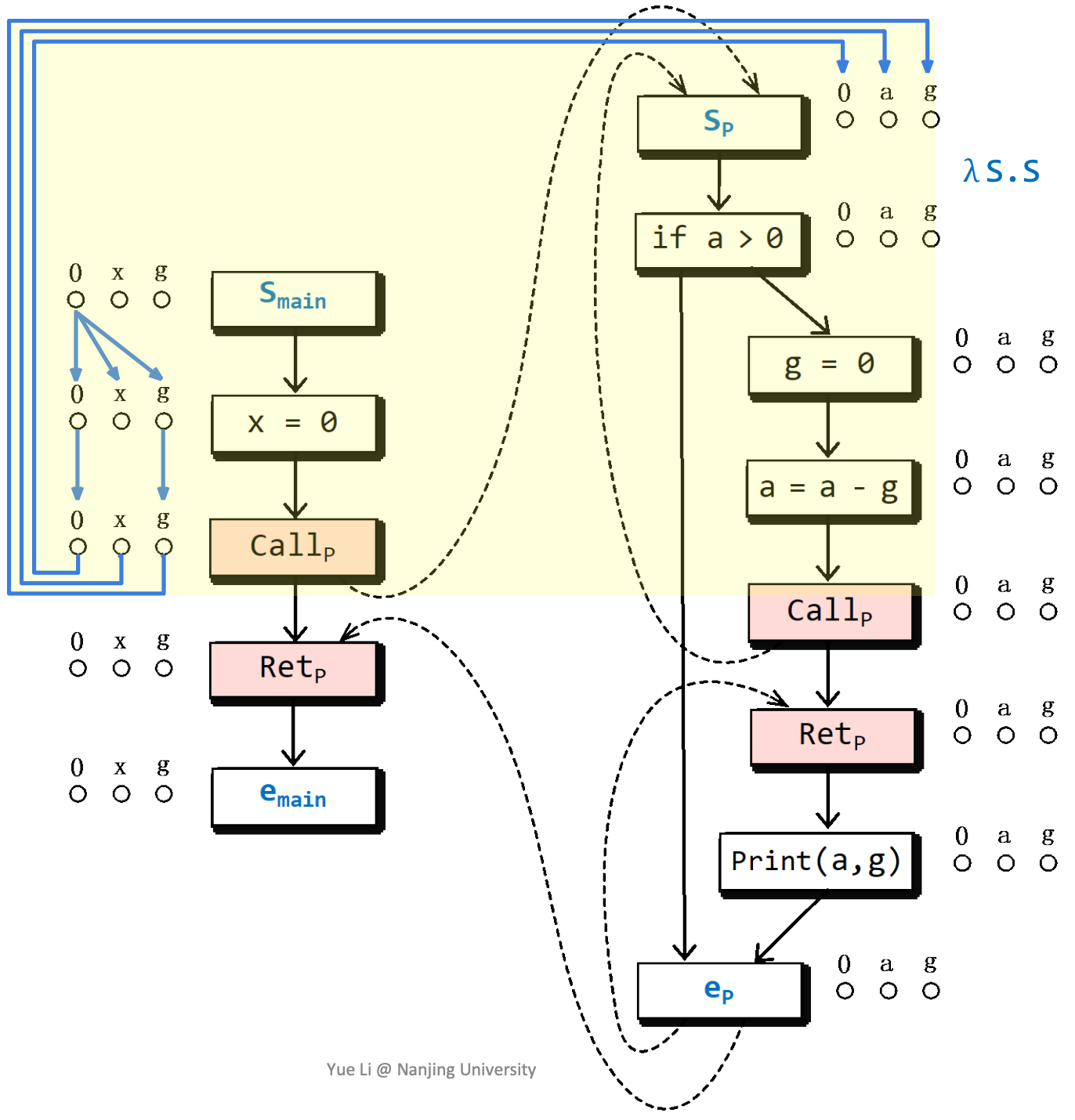
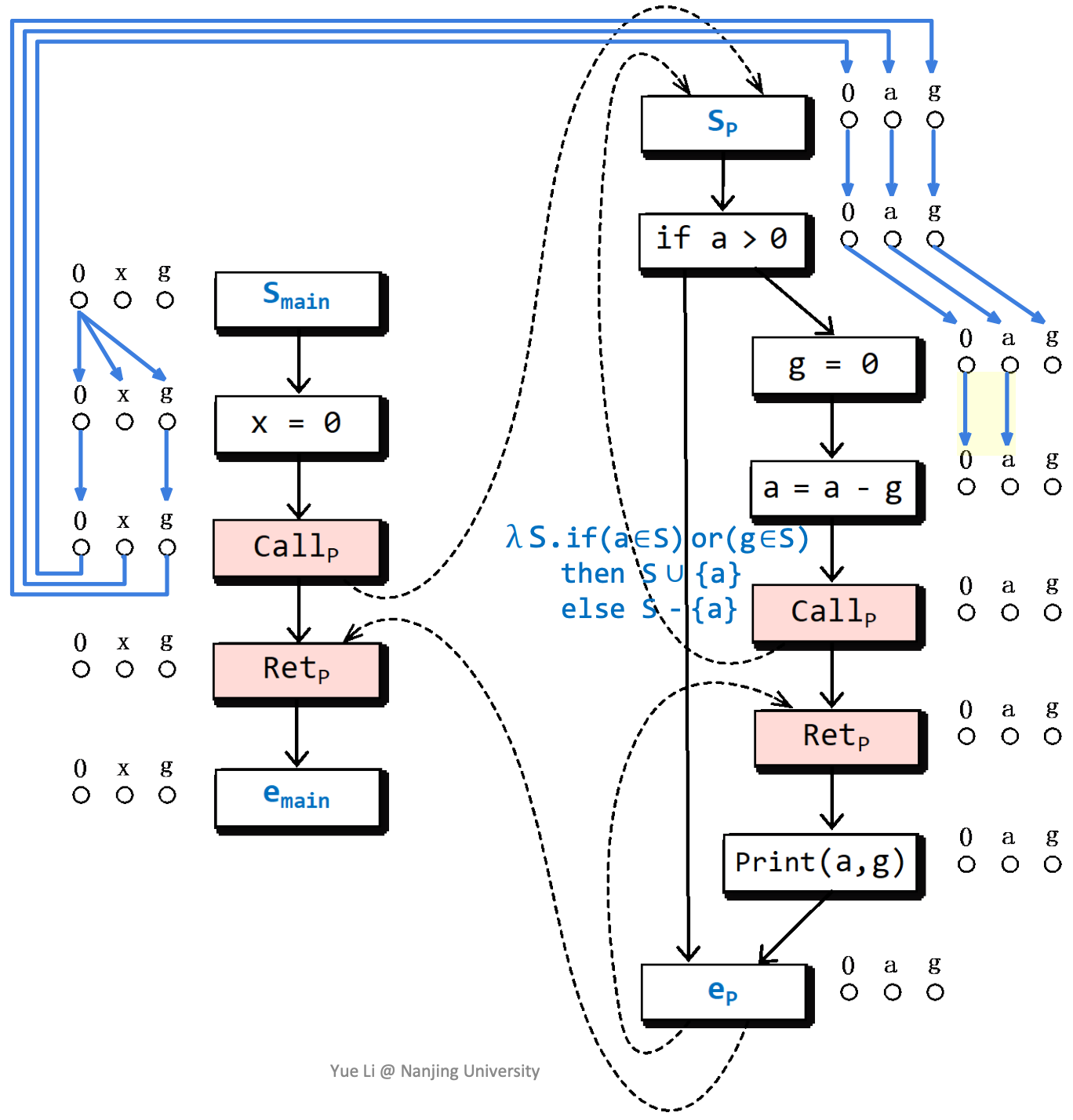
最后构造出来的Exploded Supergraph是这样的： 

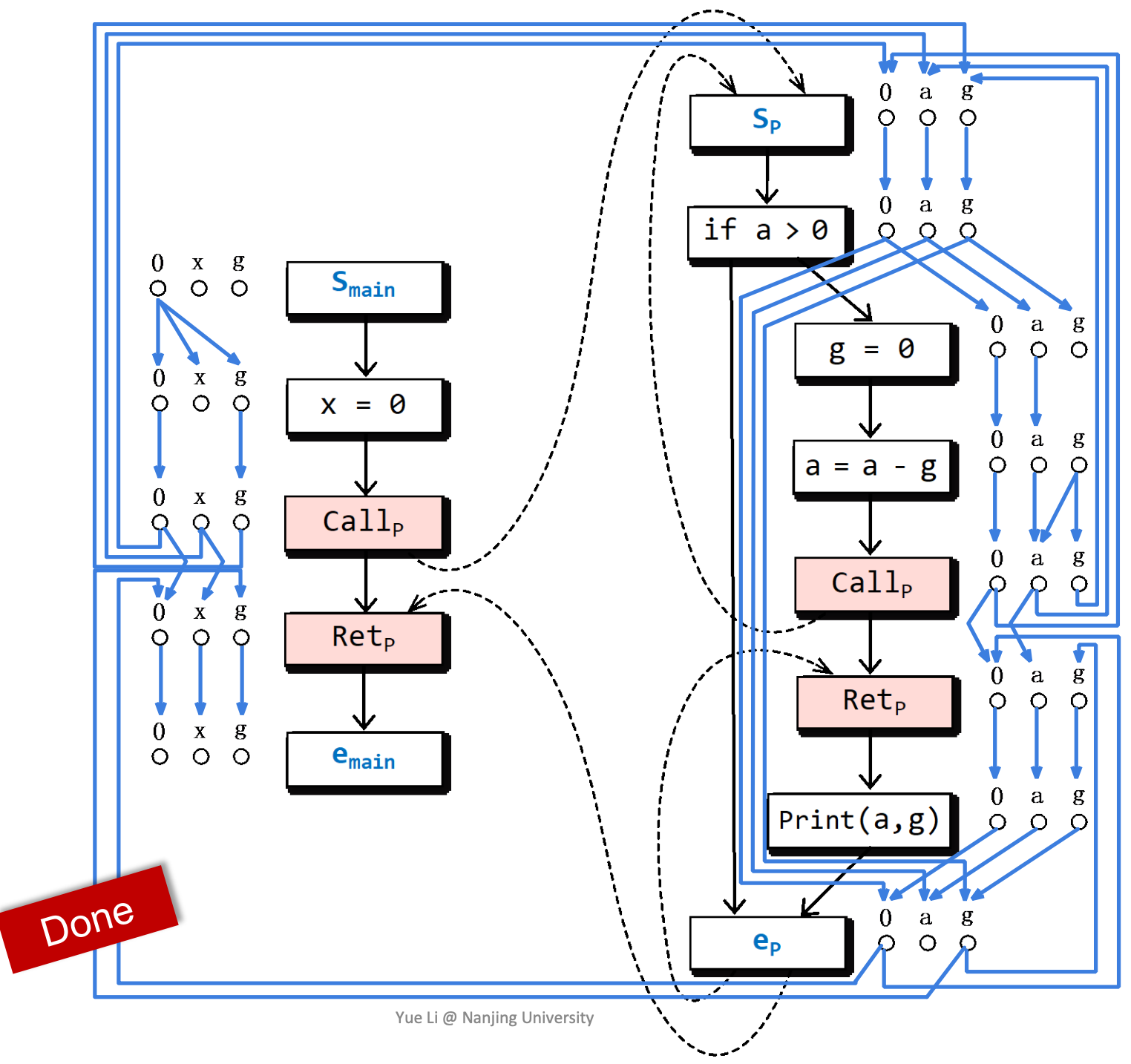
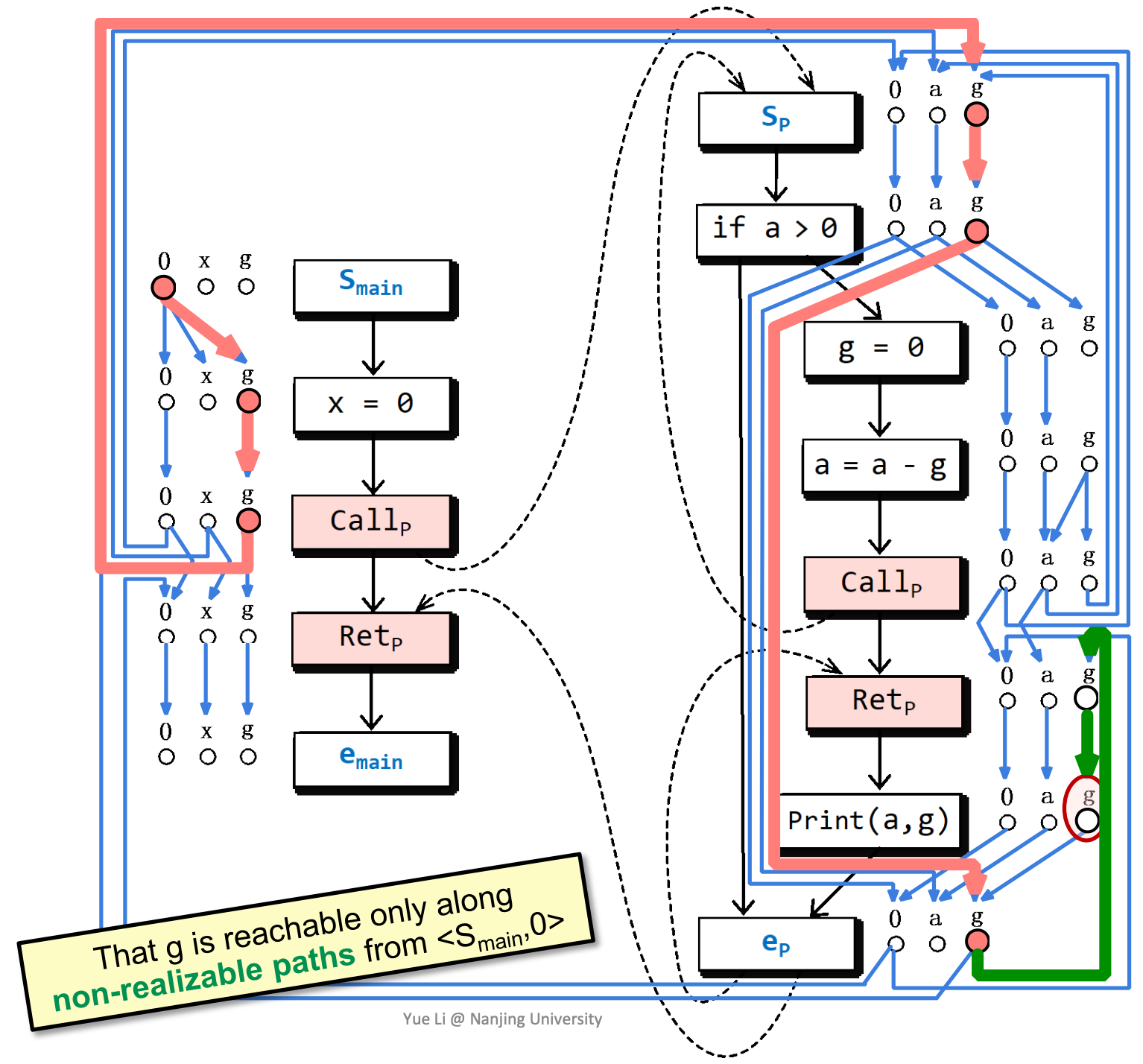
怎样使用这样的分析结果呢？我们来考虑一个问题，全局变量g在程序片段运行结束时，是否可能没有被初始化？ 

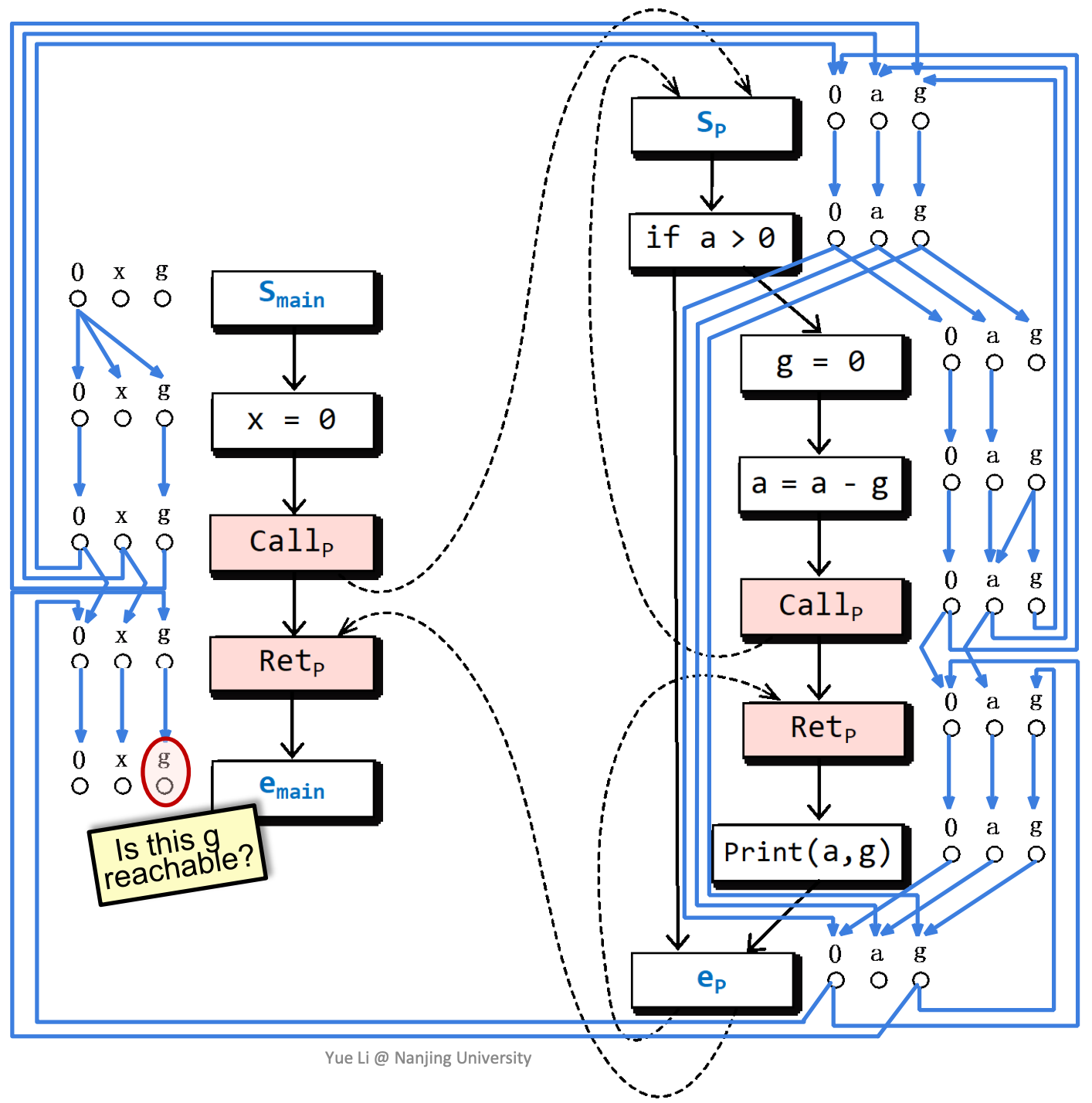
根据子图分析，g在这里可能没有被初始化。 

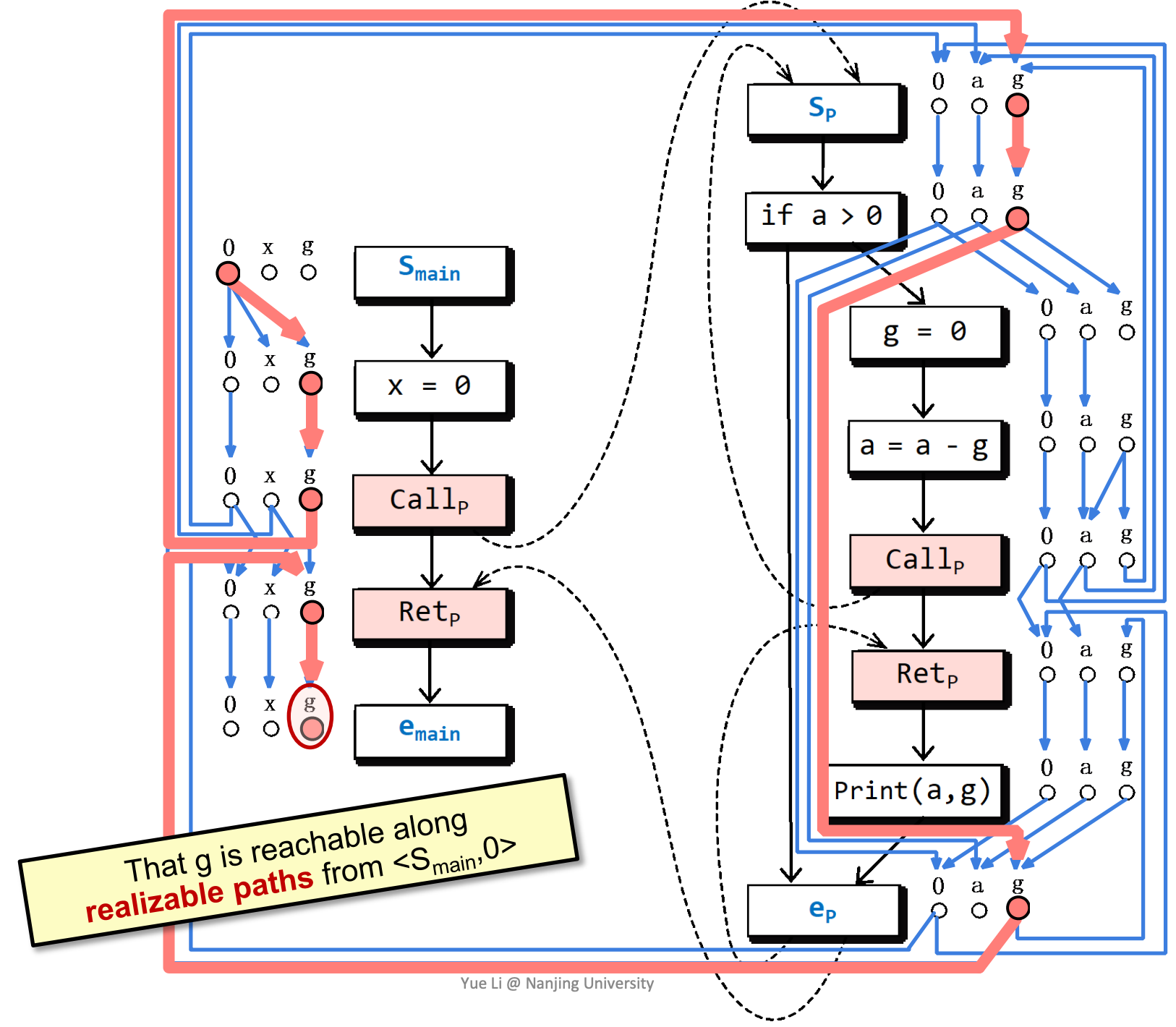
realizable path在这里也能提供更高的精度。

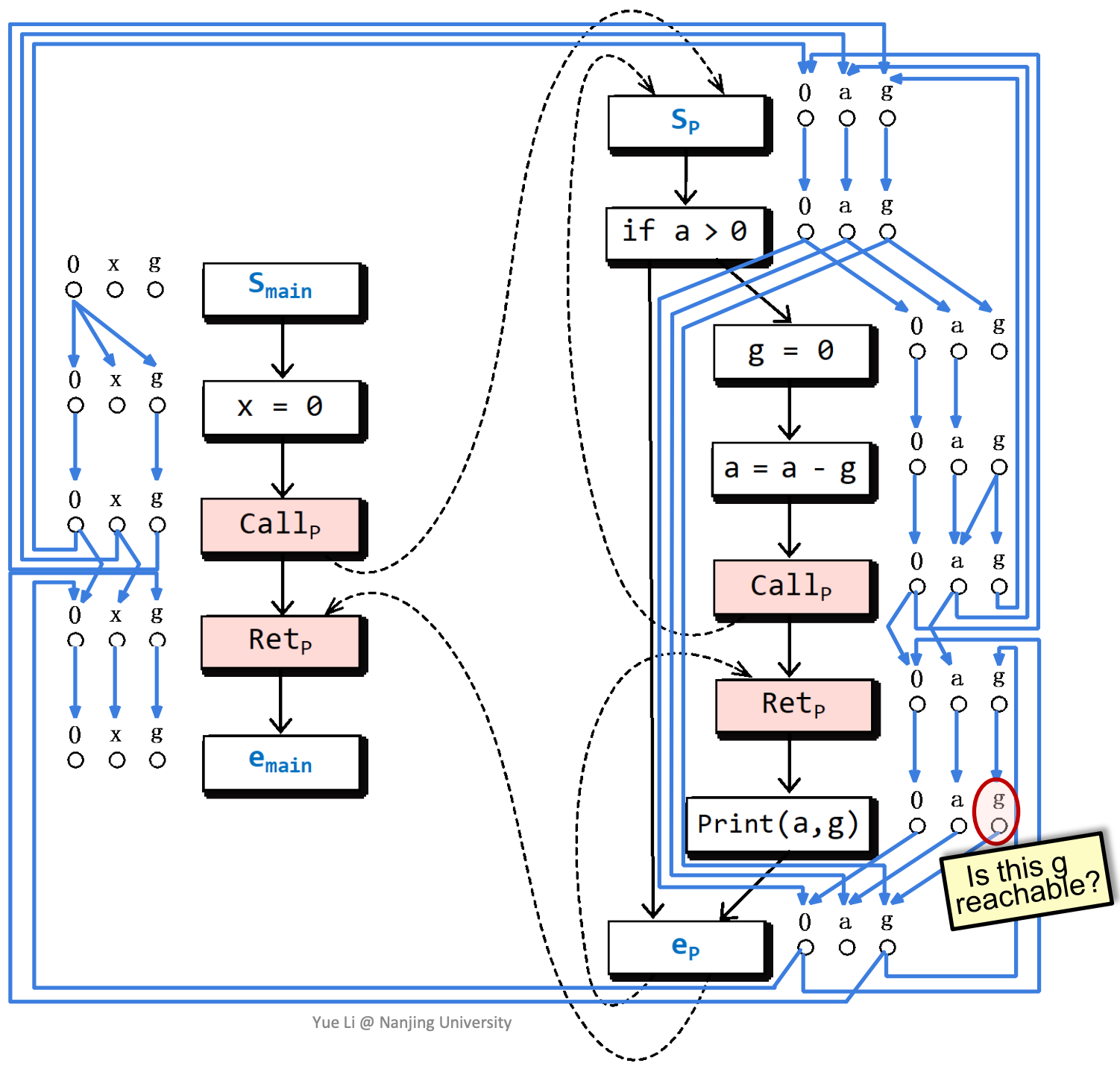
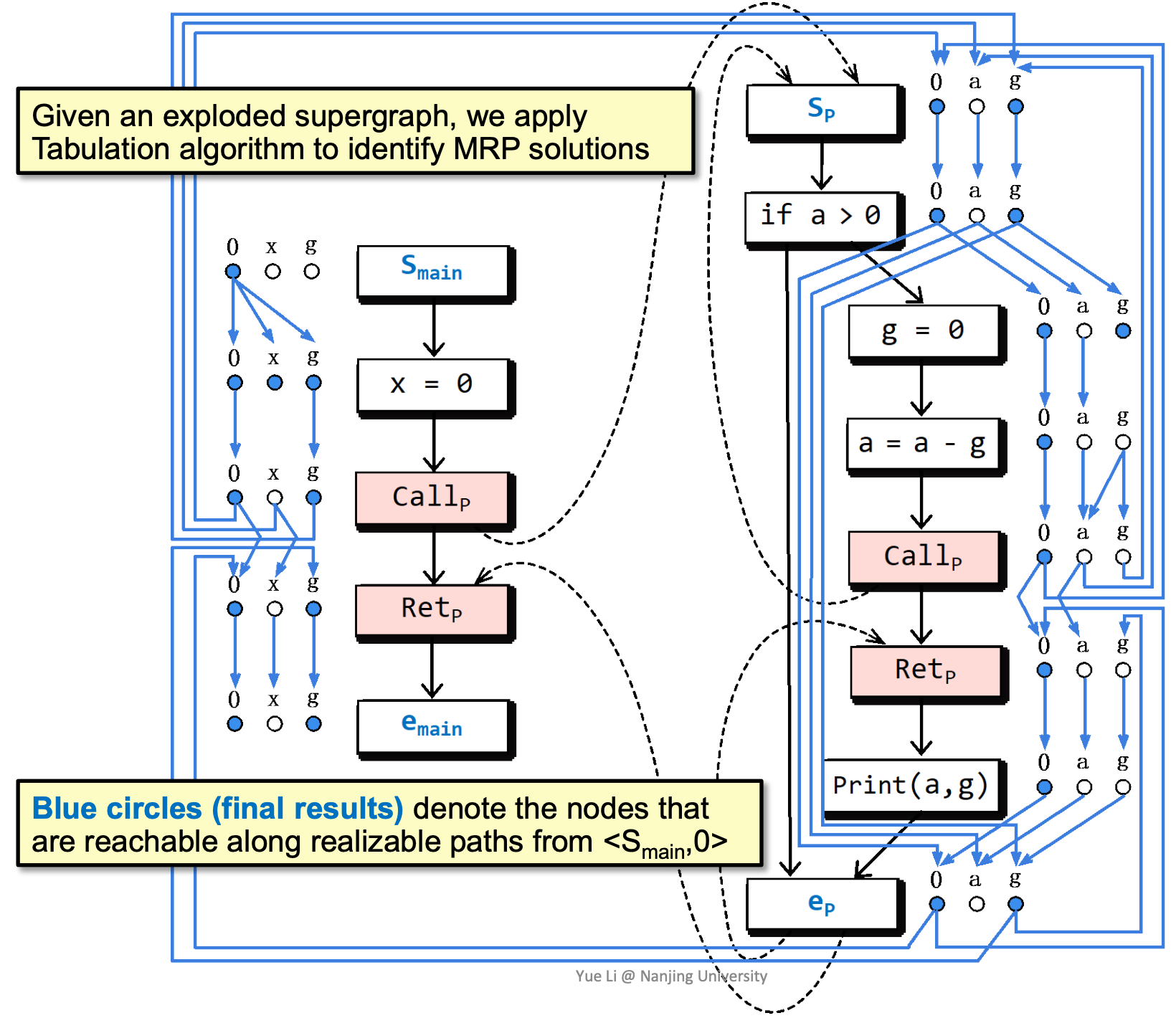
Tabulation Algorithm

用Tabulation算法，可以在O(ED³)复杂度（E为Edge的数量，D为Data facts的数量，如在下面的例子中，D为3）下得到MRP的结果： 

 

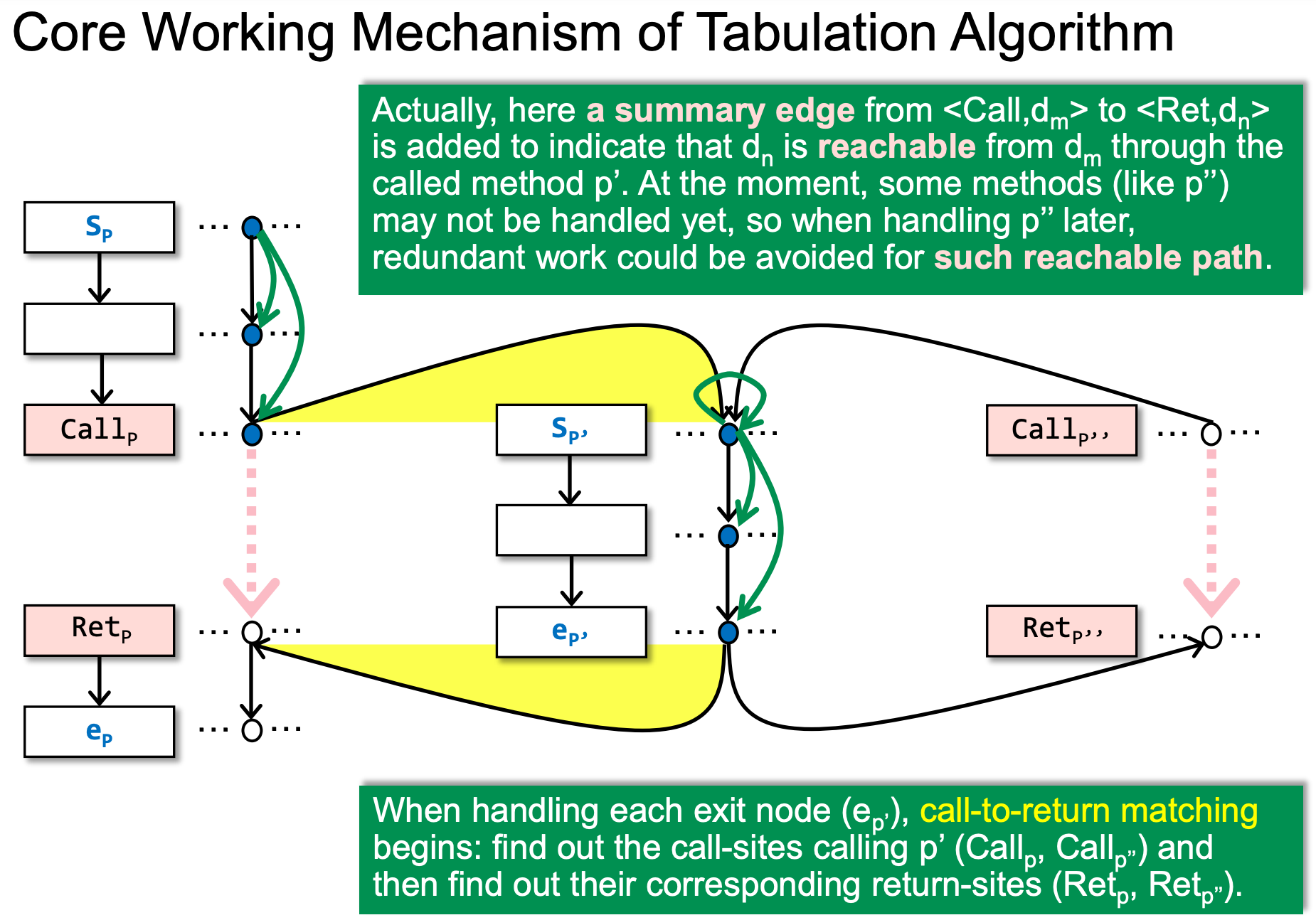
六、Understanding the Distributivity of IFDS

能够使用IFDS的条件

转化函数（流函数）是否满足分配律（F(x ^ y)=F(x) ^ F(y)）决定了是否能使用IFDS来解决这个问题。

• IFDS框架一次只能表示1个变量，即只能表示“如果x。。。，那么xxx”；无法表示“如果x和y都。。。，那么xxx”这种关系。例如，对于常量传播问题，遇到z=x+y的情况，不能表示x和y同时都是常量的情况，所以IFDS无法处理。
• 换句话说，IFDS的流函数种，每一个data fact（状态）都是相互独立的，输出不能依赖于多个输入。

上图最后的问题答案是可以使用IFDS，因为只需要考虑单一的输入即可决定输出。 

另外，IFDS无法处理指针分析：

注意图中的虚线部分，由于没有别名(alias)信息，这个边是无法被IFDS框架分析出来的。而IFDS是无法处理别名信息的，因为别名信息的另一种意义是“x和y都指向同一个对象”——这需要我们同时考虑x和y来决定他们是否指向同一个对象。