南京大学 静态软件分析（static program analyzes）-- Data Flow Analysis：Applications 学习笔记

一、Overview of Data Flow Analysis

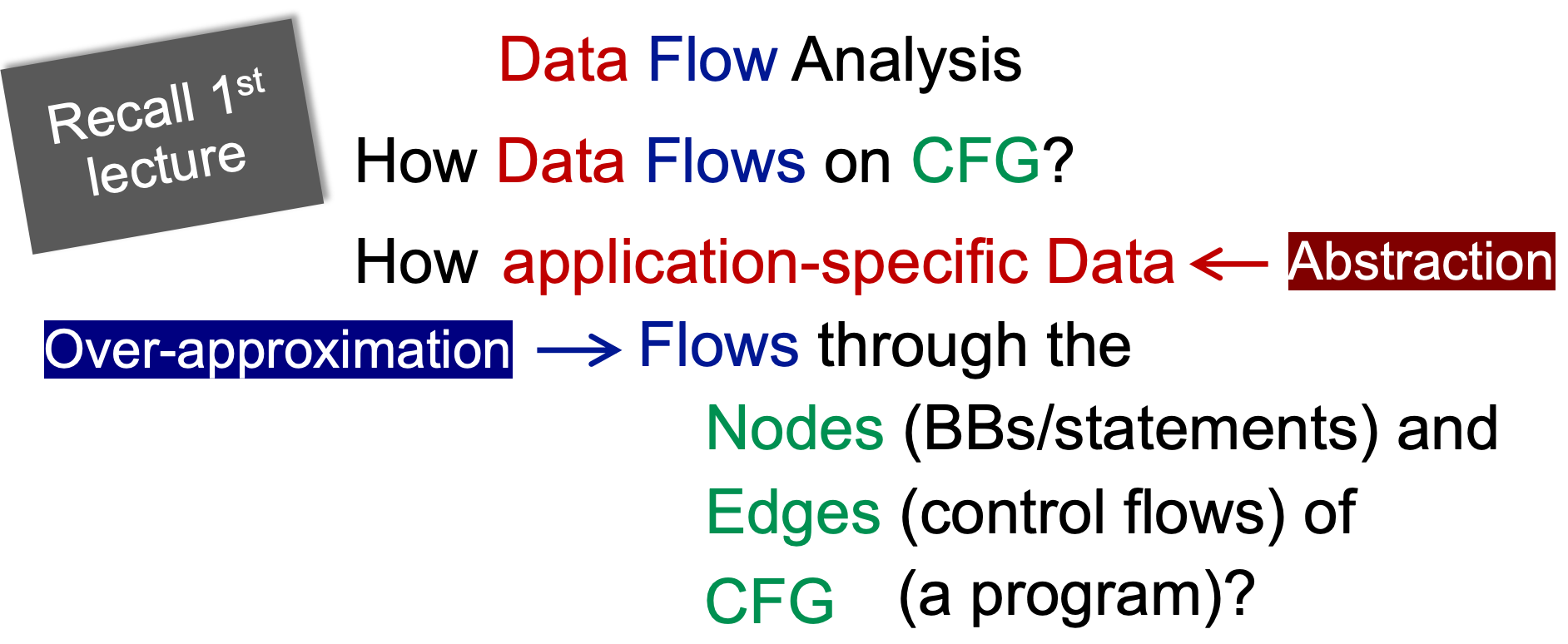
将“Data Flow Analysis”展开：

• application-specific Data：数据流分析的对象是「特定任务语境下的抽象符号数据」，例如污点分析中的“污点信息”
• Flows：Over-approximation，根据分析的类型，进行合适的符号执行
  • Nodes (BBs/statements)：如何对BBs进行transfer
  • Edges (control flows)：控制流如何处理，例如两个控制流汇入一个BB

不同的数据流分析，有着不同的「data abstraction」、「flow safe-approximation策略」、「transfer functions」、「control-flow handlings」。

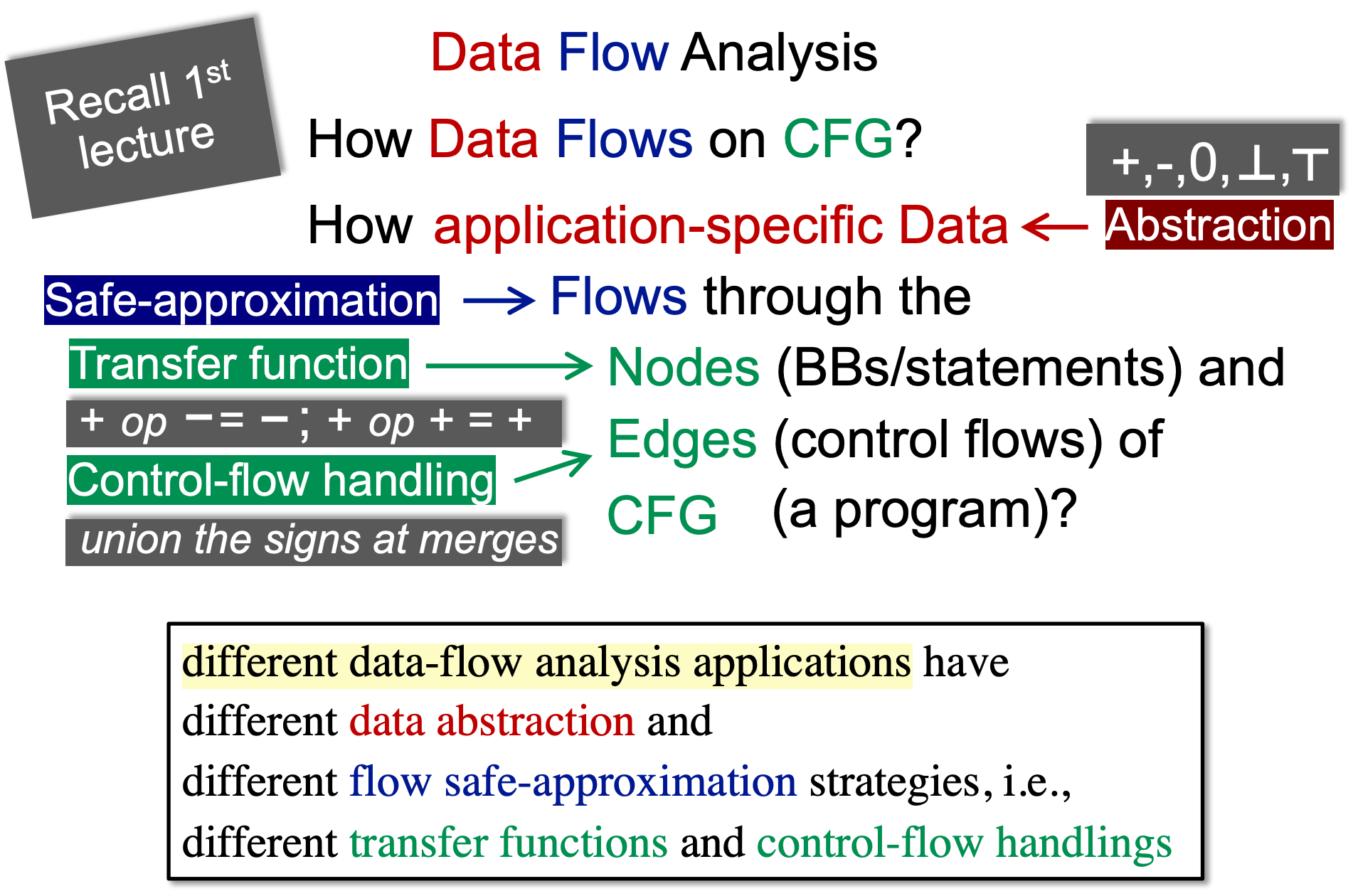
数据流分析分为may analysis和must analysis：

• may analysis报告出的结果可能正确，一般有误报（覆盖率更大，甚至能覆盖所有情况；soundness程度比较大，但也不是全部soundness）；具体：多个前驱只要有一个传入就行（并）
• must analysis报告出的结果一定正确，但一般有漏报（保证了precision）；具体：多个前驱必须都传入才行（交）

 

二、Preliminaries of Data Flow Analysis

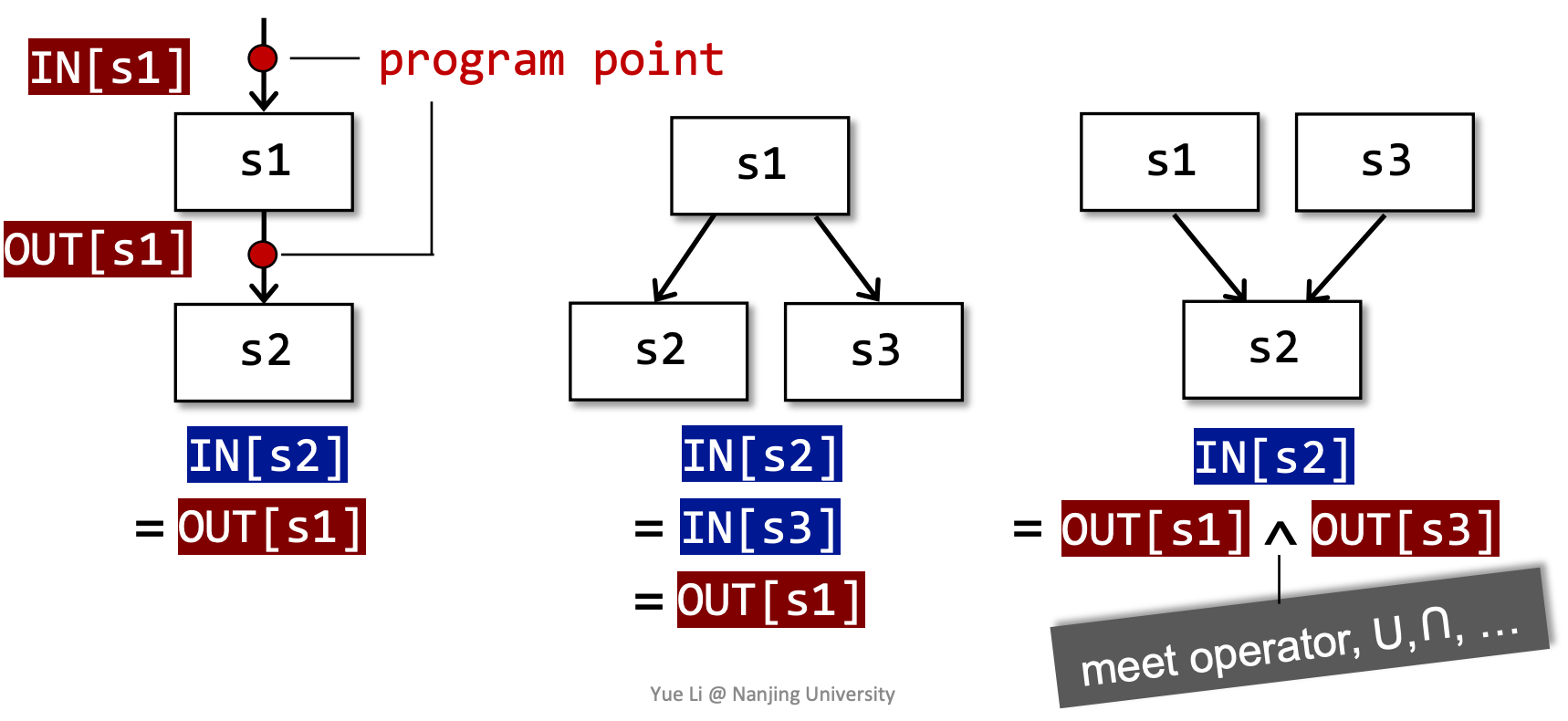
Input and Output States 输入输出状态

• 每一条IR的执行，都会使状态从输入状态变成新的输出状态
• 输入/输出状态与语句前/后的 program point 相关联

In each data-flow analysis application, we associate with every program point a data-flow value that represents an abstraction of the set of all possible program states that can be observed for that point.

在数据流分析中，我们会把每一个PP关联一个数据流值，代表在该点中可观察到的抽象的程序状态，每一个PP点所观察到程序状态都是不同的。

还是以Webshell污点分析为例，

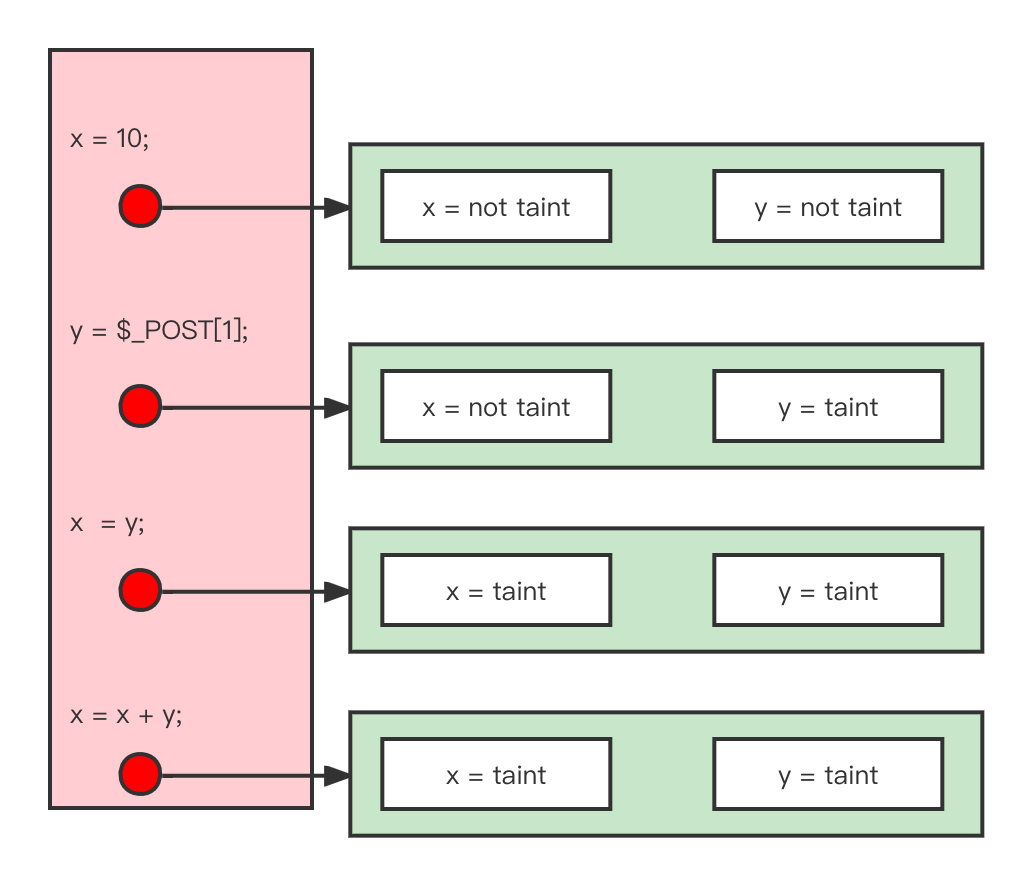
Data-flow analysis is to find a solution to a set of safe-approximationdirected constraints on the IN[s]’s and OUT[s]’s, for all statements s.

• - constraints based on semantics of statements (transfer functions)
• - constraints based on the flows of control

关于转移方程约束的概念

分析数据流有前向和后向两种：

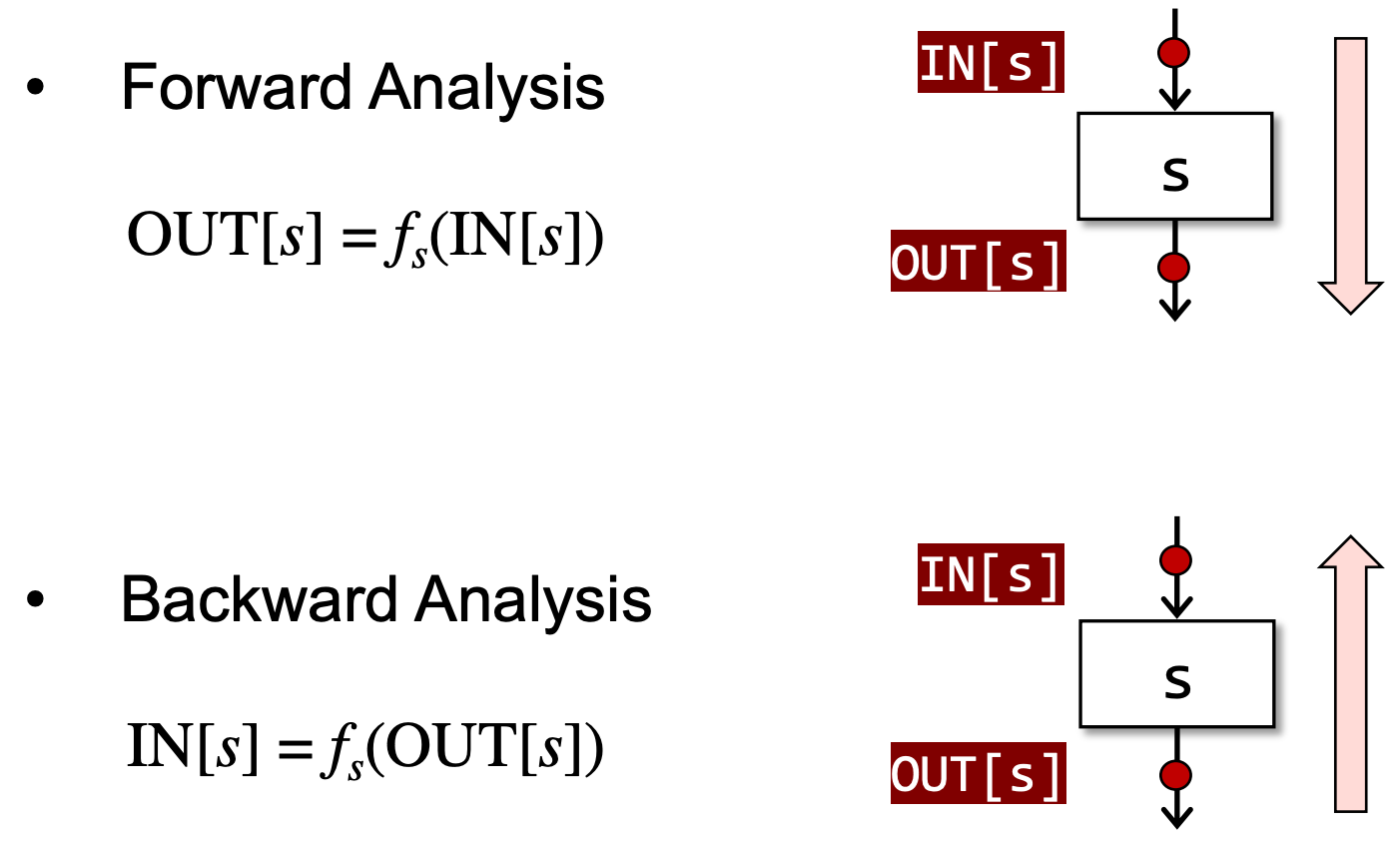
关于控制流约束的概念

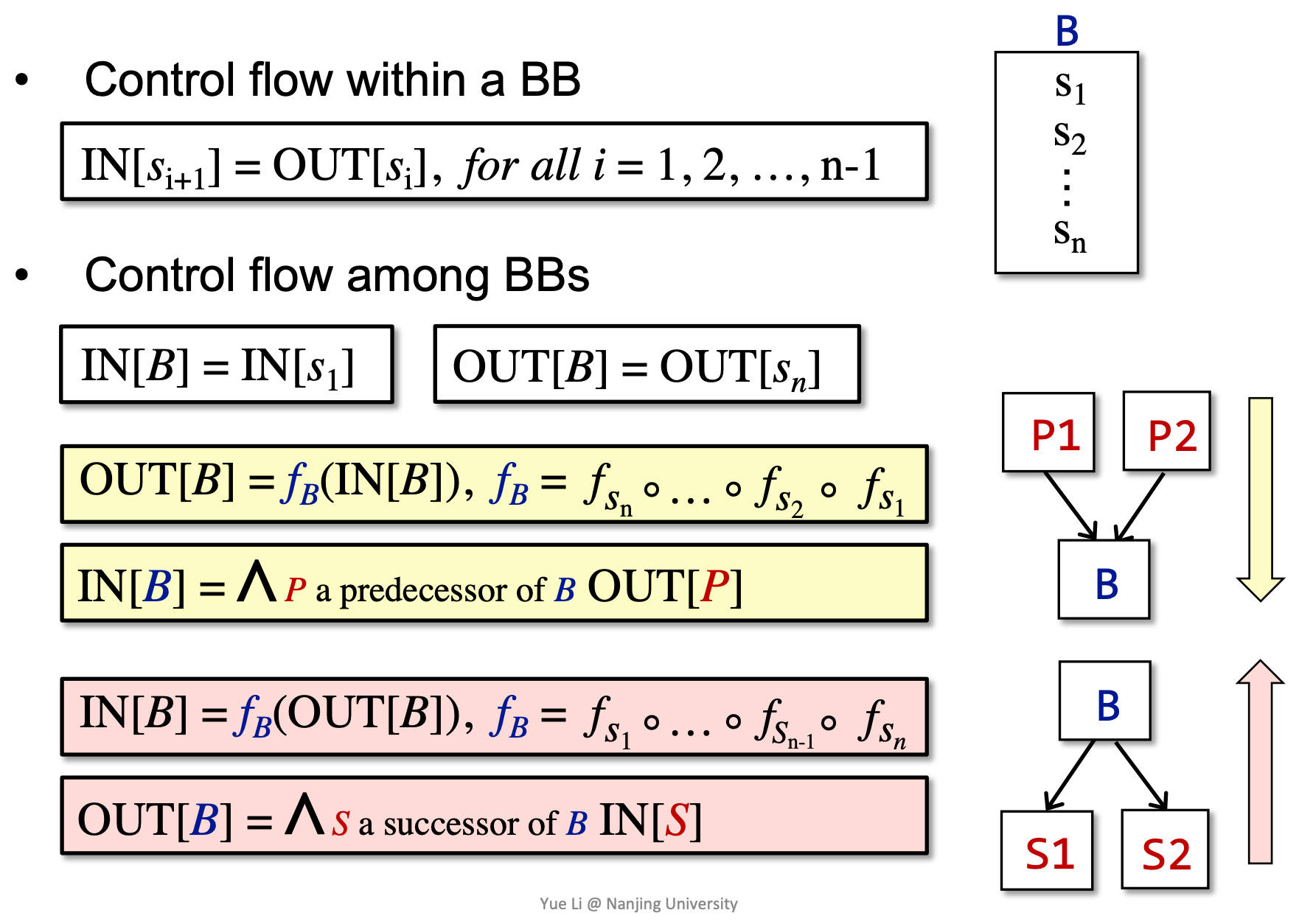
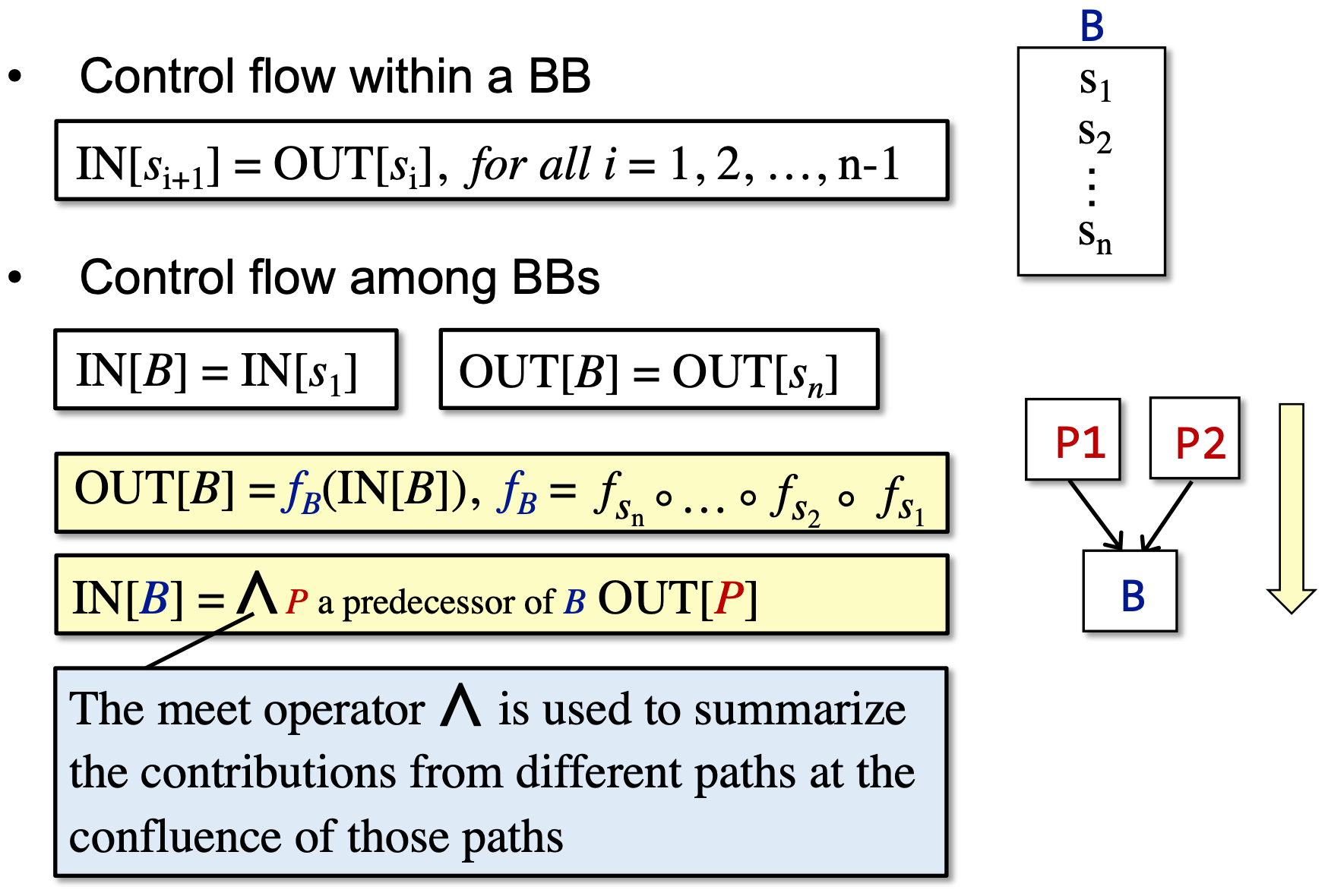
每条语句 s 都会使程序状态发生改变。
B 的输出自然是其输入在经过多次转换后得到的状态。
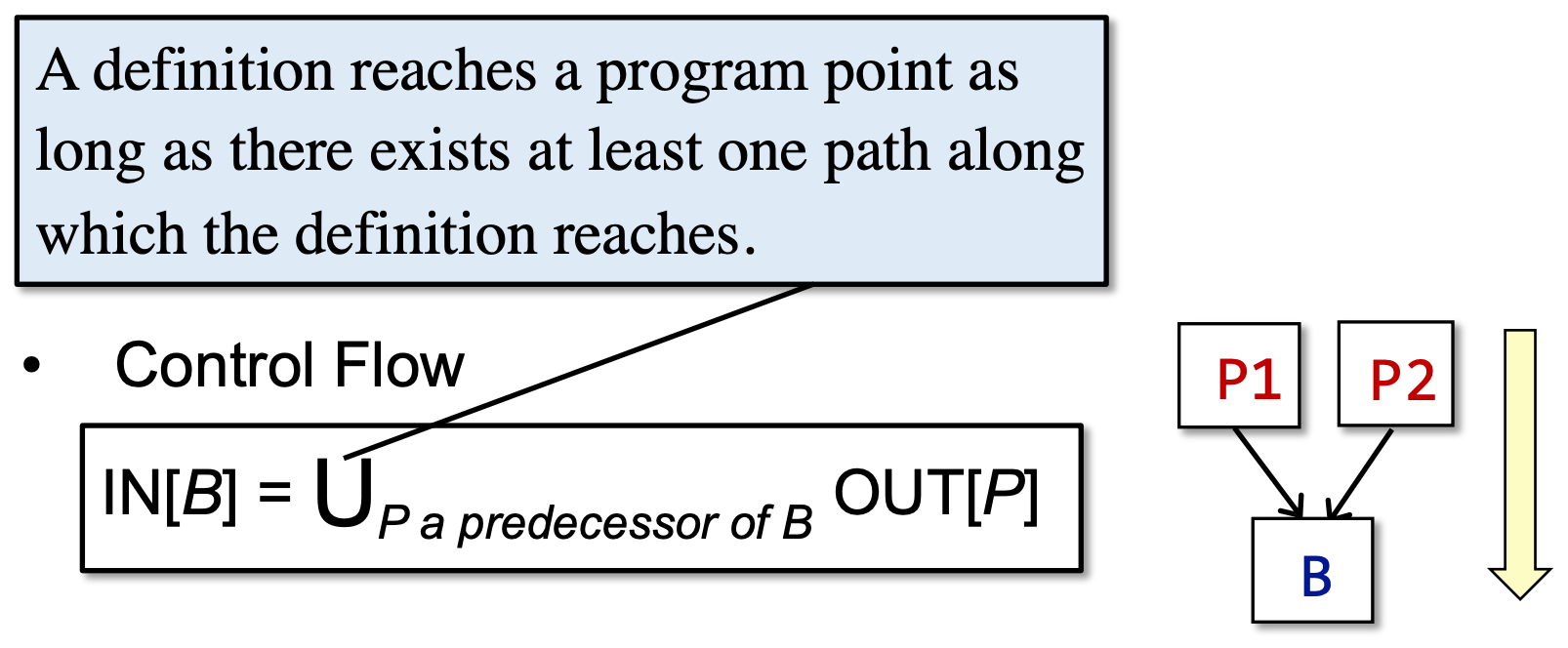
而 B 的输入要根据数据流分析的需求，对其前驱应用合适的 meet operator 进行处理。后向分析时亦然。

 

三、Reaching Definitions Analysis

基本概念

Reaching Definitions定义：

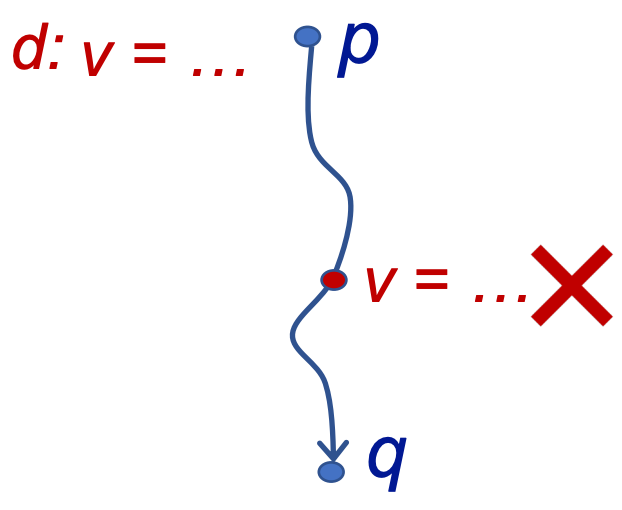
• A definition d at program point p reaches a point q if there is a path from p to q such that d is not “killed” along that path. 给变量v一个定义d（赋值），存在一条路径使得程序点p处的定义能够到达q，且在这个过程中没有改变v的赋值（没有对其进行赋值），则程序在p点“定义可达”。该分析为may analysis，会把可能到达的情况都统计进去（即使是条件跳转）。定义可达表示没有被赋值，是危险的
  • 对于一条赋值语句 D: v = x op y，该语句生成了 v 的一个定值 D，并杀死程序中其它对变量 v 定义的定值。
  • 假定 x 有定值 d₁ (definition)，如果存在一个路径，从紧随 d₁ 的点到达某点 p，并且此路径上面没有 x 的其他定值点，则称 x 的定值 d 到达 (reaching) p；如果在这条路径上有对 x 的其它定值d₂，我们说变量 x 的这个定值 d 被杀死 (killed) 了，被谁杀死了呢，被定值d₂杀死了

以下面这段程序为例，

p point
B1 {
    x = 1: D1
    y = 2: D2
}
B2 {
    x = 3: D3
    y = 4: D4
}
q point

初始状态下，整个程序的Definitions的数据流值bit vector为：0000

• 在p point，x、y有两个definition，分别为D1、D2，此时bit vector为：1100
• 在 q point，x、y又有两个definition，分别为D3、D4，D1、D2则“kill”掉了，此时bit vector为：0011

每个PP中，Reaching Definitions的数据流值bit vector定义：

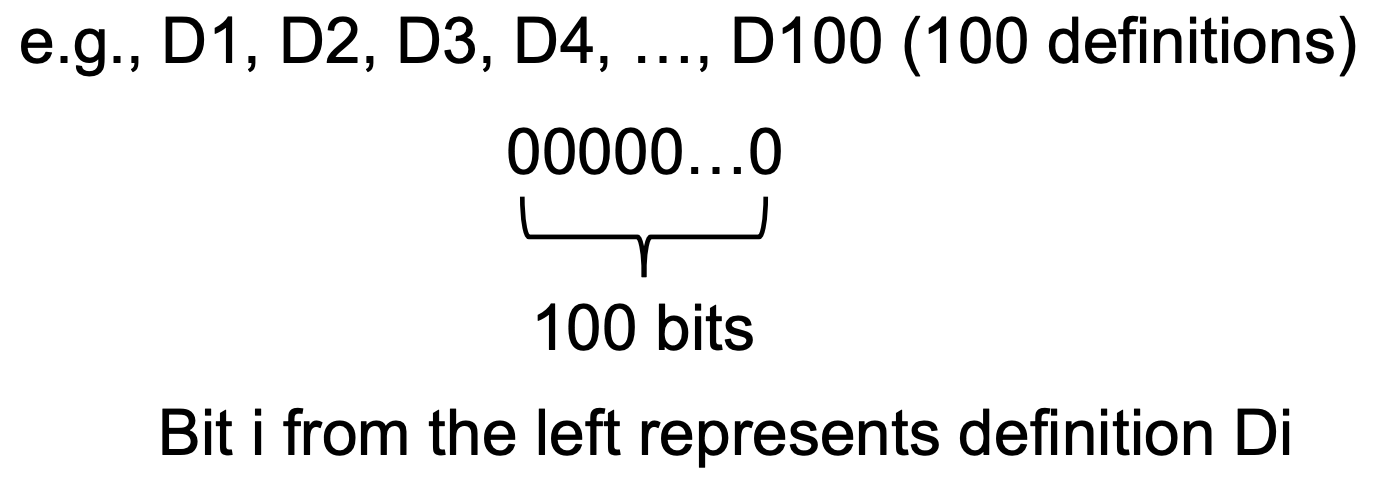
程序中每一行的变量赋值语句都对应一个definition，有多少变量赋值，就有多少definition，我们将程序中所有的definition都汇总起来，统一用一个 bit vector 来定义，有多少个赋值语句，就有多少个位。 

 

 

之所以要这么定义的原因，是因为在每个program point中，由于BBs会有对变量的赋值操作，程序的状态都会发生改变。

所以我们将整个程序中所有definition都拉齐到一个向量里看。这种表示方法有一个好处，就是可以清楚地看清楚在不同的pp，所有变量赋值的可达情况。

 

Reaching Definitions的Transfer Function定义：

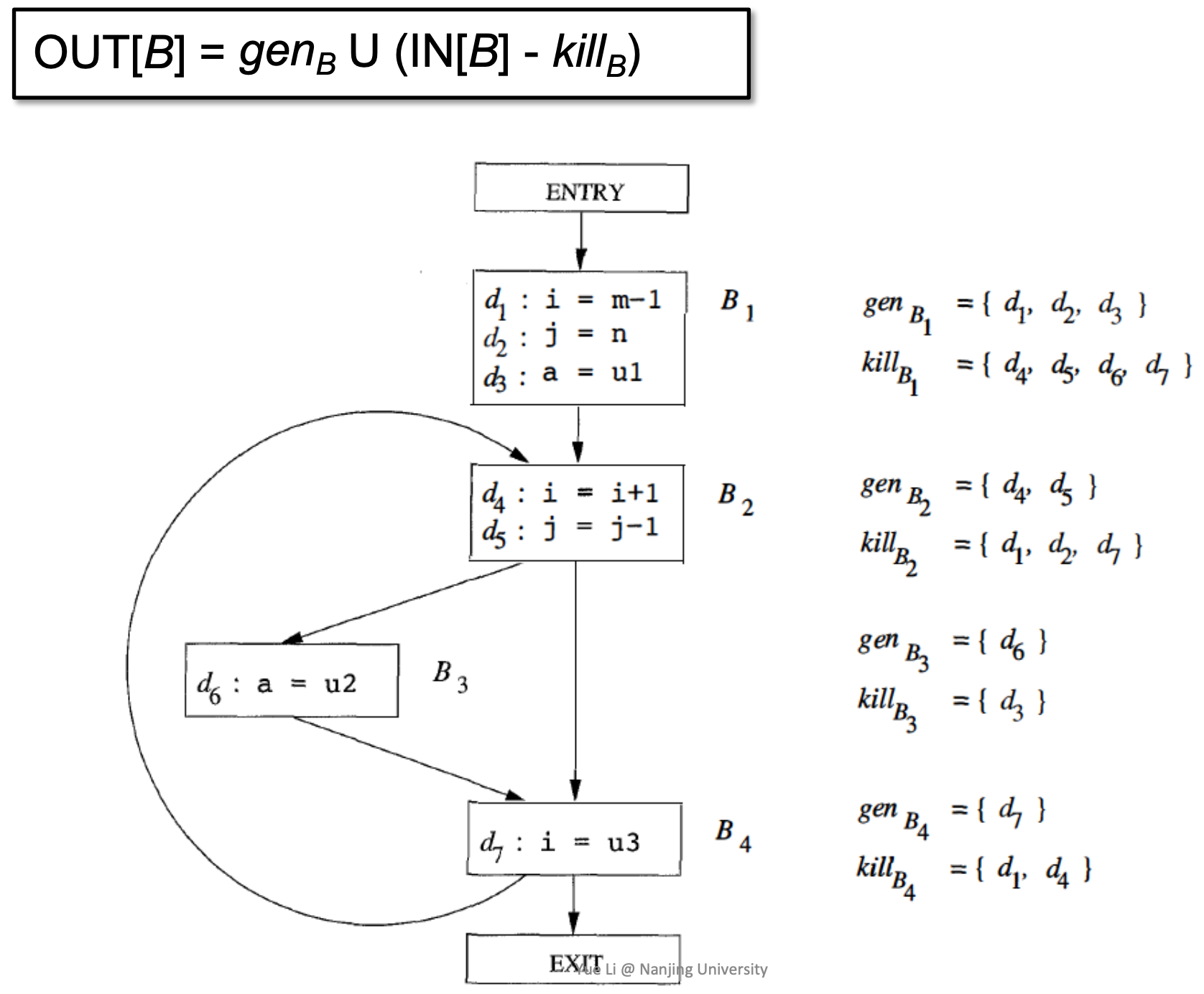
• Kill_B：“kills” all the other definitions in the program that define variable v 
• gen_B：“generates” a definition D of variable v
• gen_B U (IN[B] - kill_B)：“generates” a definition D of variable v and “kills” all the other definitions in the program that define variable v, while leaving the remaining incoming definitions unaffected. 从入口状态删除 kill 掉的定值，并加入新生成的定值。

Reaching Definitions的Control Flow定义：

 

Reaching Definitions Analysis的应用场景：

1. 变量undefined被使用检查：变量是否在使用前被赋值（以解决变量undefined问题），所以只要有可能没被赋值，就要记录下来，而不是一定的情况才记录。例如，我们在程序入口为各变量引入一个 dummy 定值。当程序出口的某变量定值依然为 dummy，则我们可以认为该变量未被定义
2. Webshell污点检测：在初始化阶段，对所有Definition进行遍历，对存在外部可控参数（taint源）的程序状态位（某个函数）标记为1。然后进行Data-Flow Analyzes，最后在特定的Program Point（敏感函数）上进行可达性分析，即分析在PP上的抽象程序状态是否存在被置为1的状态位（即存在被外部可控参数污染的变量被传到该敏感函数中）

Algorithm of Reaching Definitions Analysis

• 首先让所有BB和入口的OUT为空。因为你不知道 BB 中有哪些definition被生成。
• 当任意 OUT 发生变化，则分析出的definition可能需要继续往下流动，所需要修改各 BB 的 IN 和 OUT。
• 先处理 IN，然后再根据转移完成更新 OUT。
• 在 gen U (IN - kill) 中，kill 与 gen 相关的 bit 不会因为 IN 的改变而发生改变，而其它 bit 又是通过对前驱 OUT 取并得到的，因此其它 bit 不会发生 1->0 的收缩情况。所以，OUT 是不断增长的，而且有上界，因此算法最后必然会停止。
• 因为 OUT 没有变化，不会导致任何的 IN 发生变化，因此 OUT 不变可以作为终止条件。我们称之为程序到达了不动点（Fixed Point）

我们用一个实际的例子来说明这个循环处理过程。

下图中，每一轮循环中，Reaching Definitions bit vector的变化情况我们分别用不同的颜色表示，

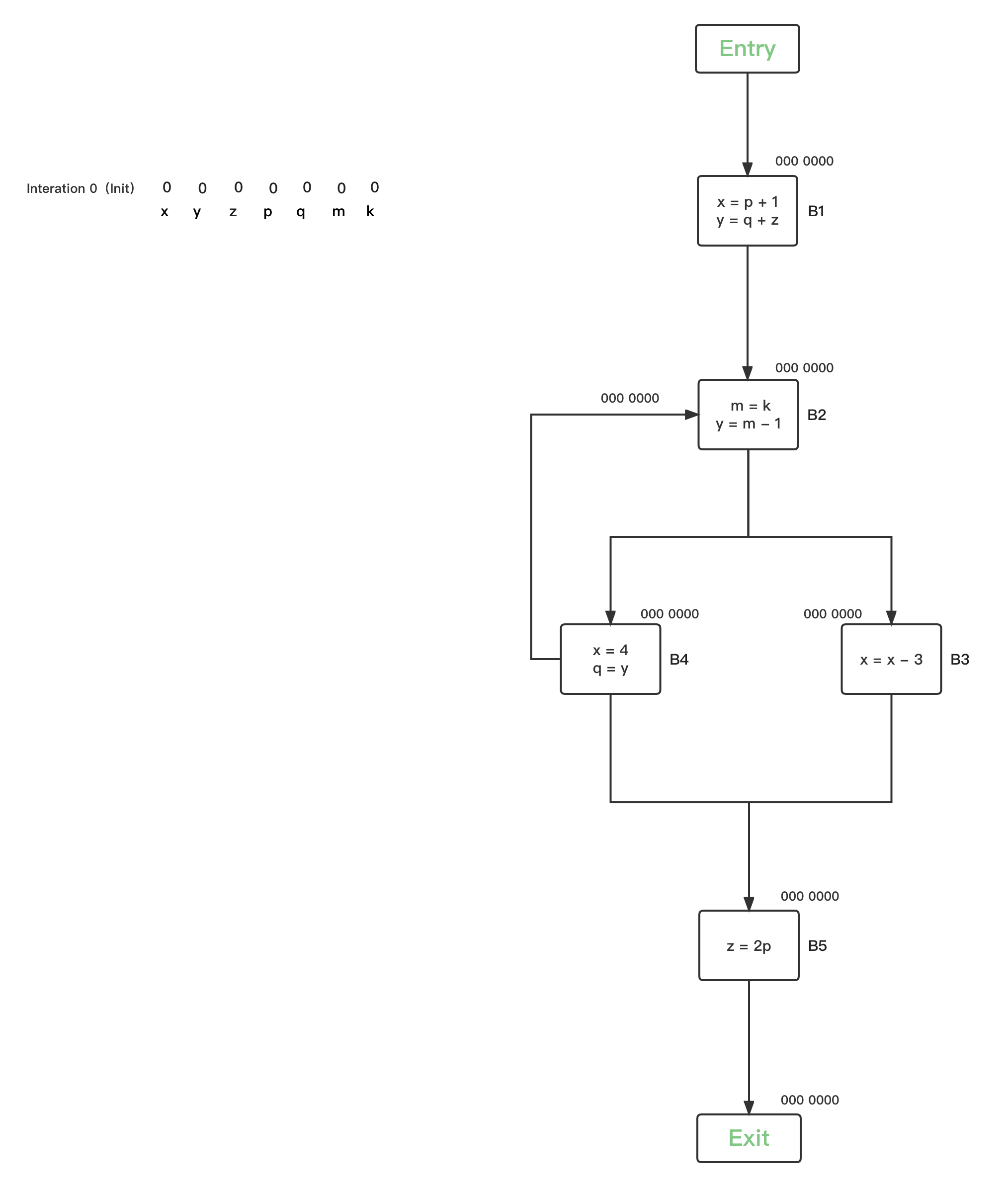
• 第一轮循环，将所有BBs的Reaching Definitions bit vector都初始化为0：

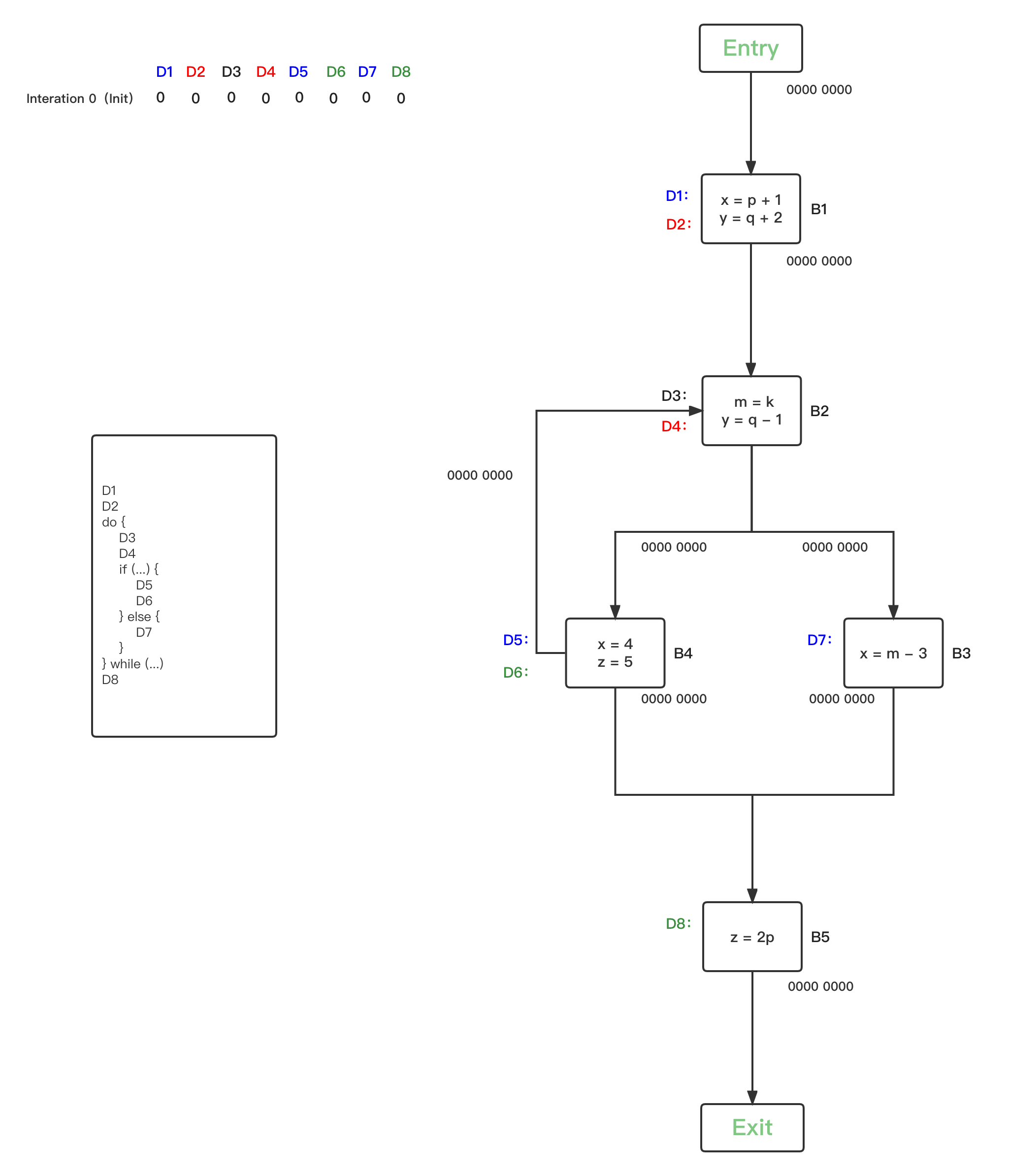
上图左边是程序伪码，右边是对应的CFG图，总共有{B1、B2、B3、B4、B5} 5个BBs，针对程序中的变量，在不同的PP分别定义了Definitions，

• x：{D1、D5、D7}：蓝色
• y：{D2、D4}：红色
• m：{D3}：黑色
• z：{D6、D8}：绿色

Reaching Definitions的数据流值bit vector初始化定义为：

在每一个PP状态点，都有一个对应的Reaching Definitions bit vector状态。

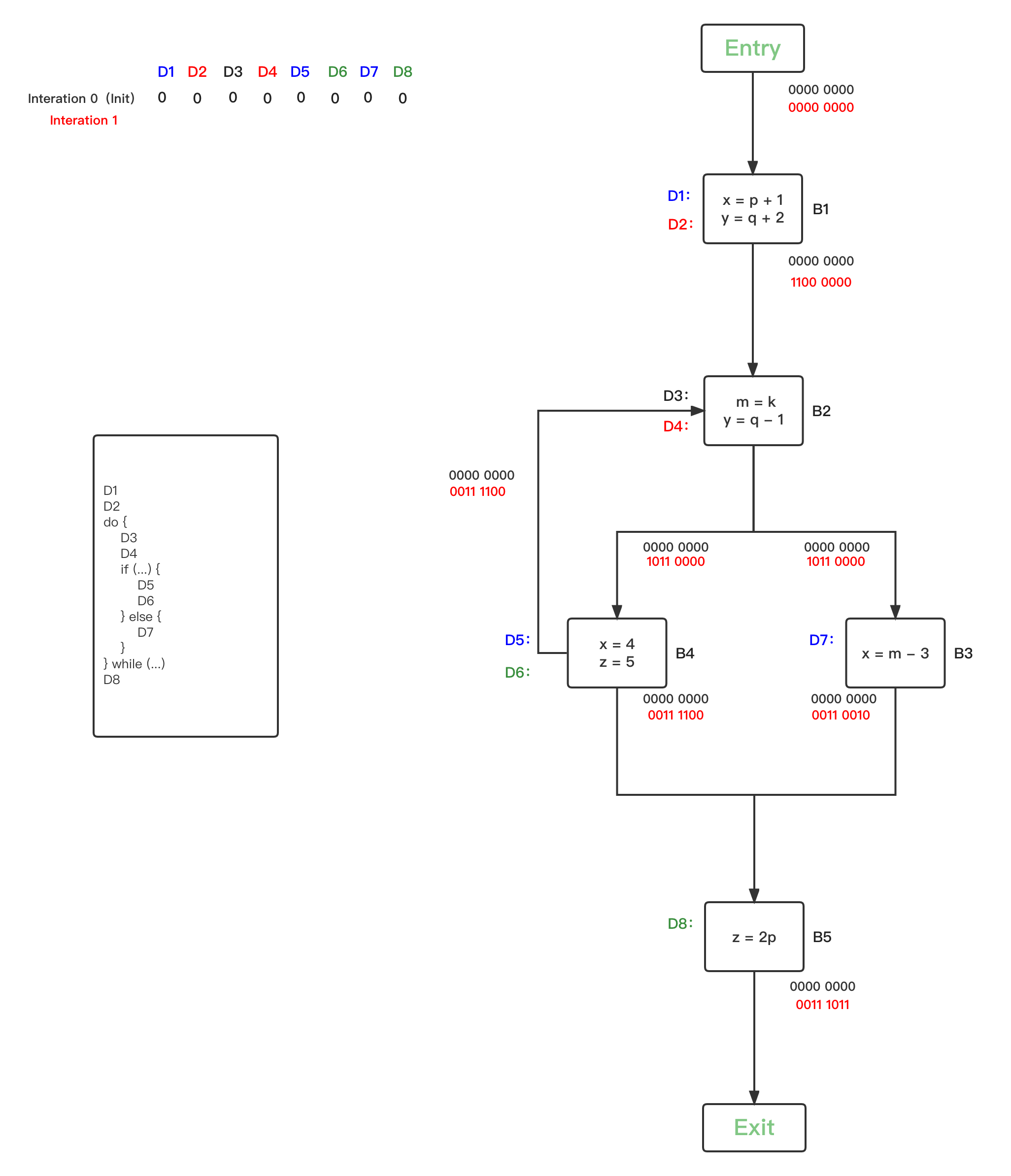
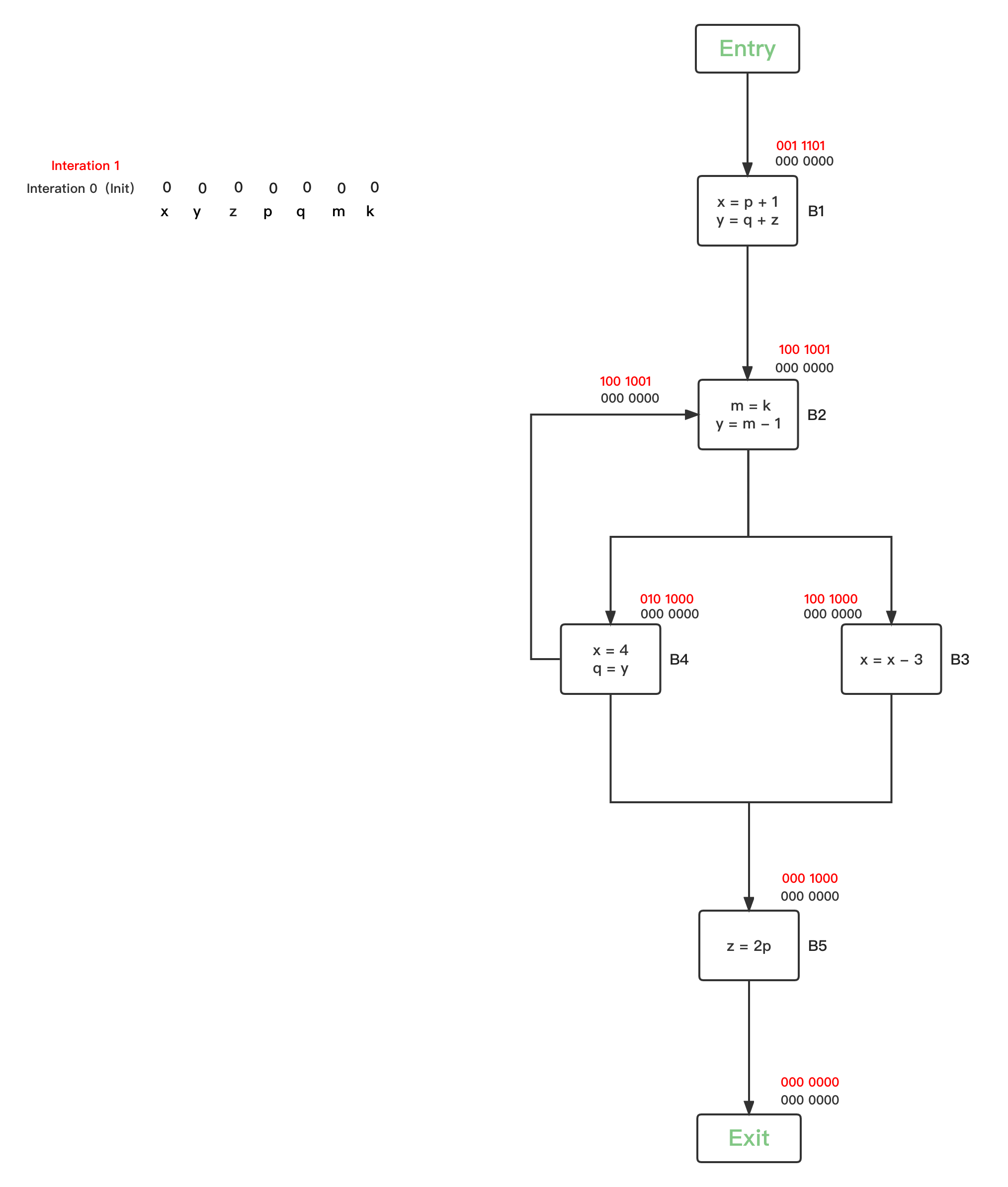
• 第二轮循环，因为所有的BBs的Reaching Definitions bit vector都被初始化改变了，因此每一个BBs都要进行safe-approximation分析：

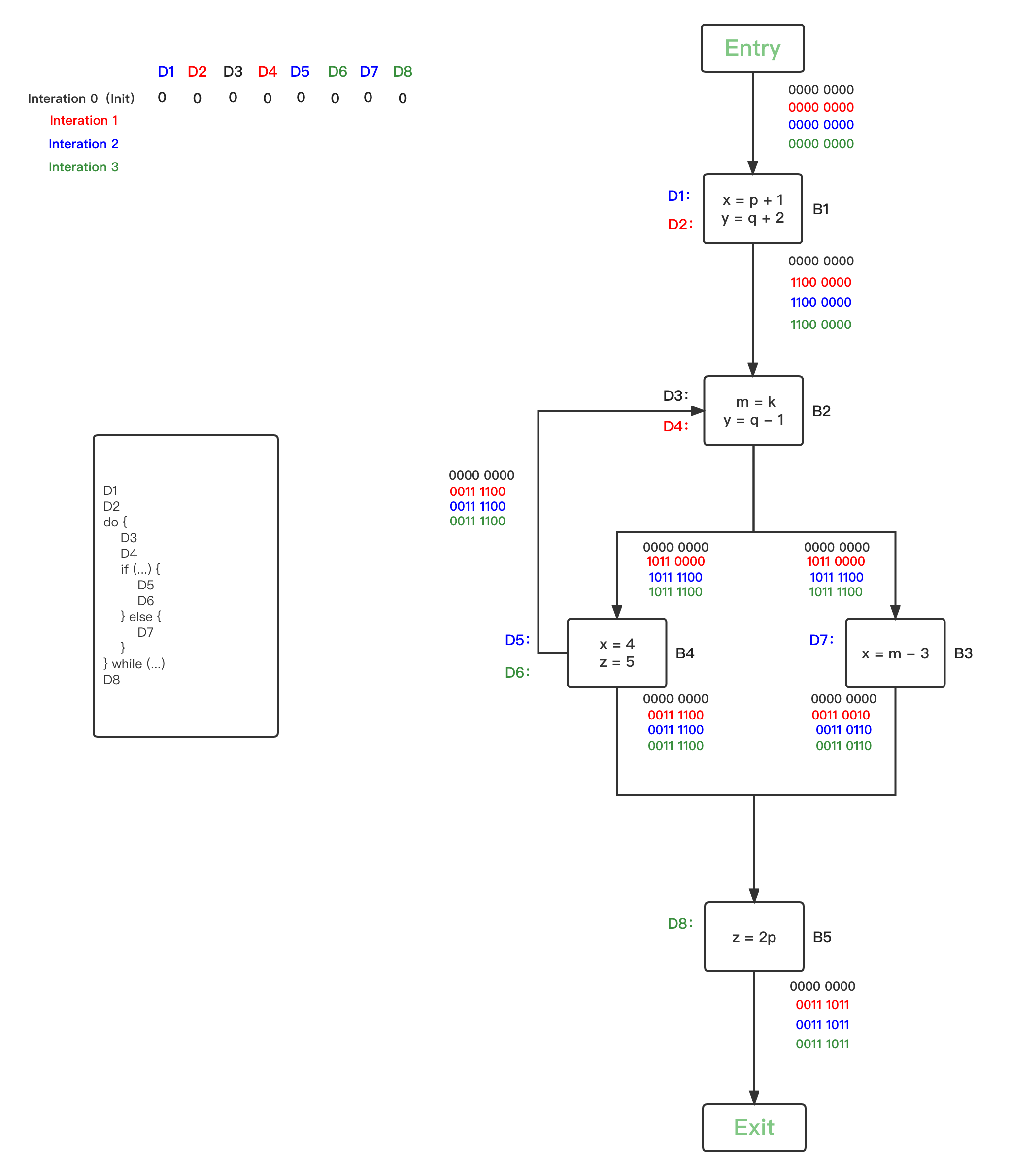
• 第三轮循环，统计上一轮发生OUT改变的的BBs有{B1、B2、B3、B4、B5}，继续逐一safe-approximation分析：

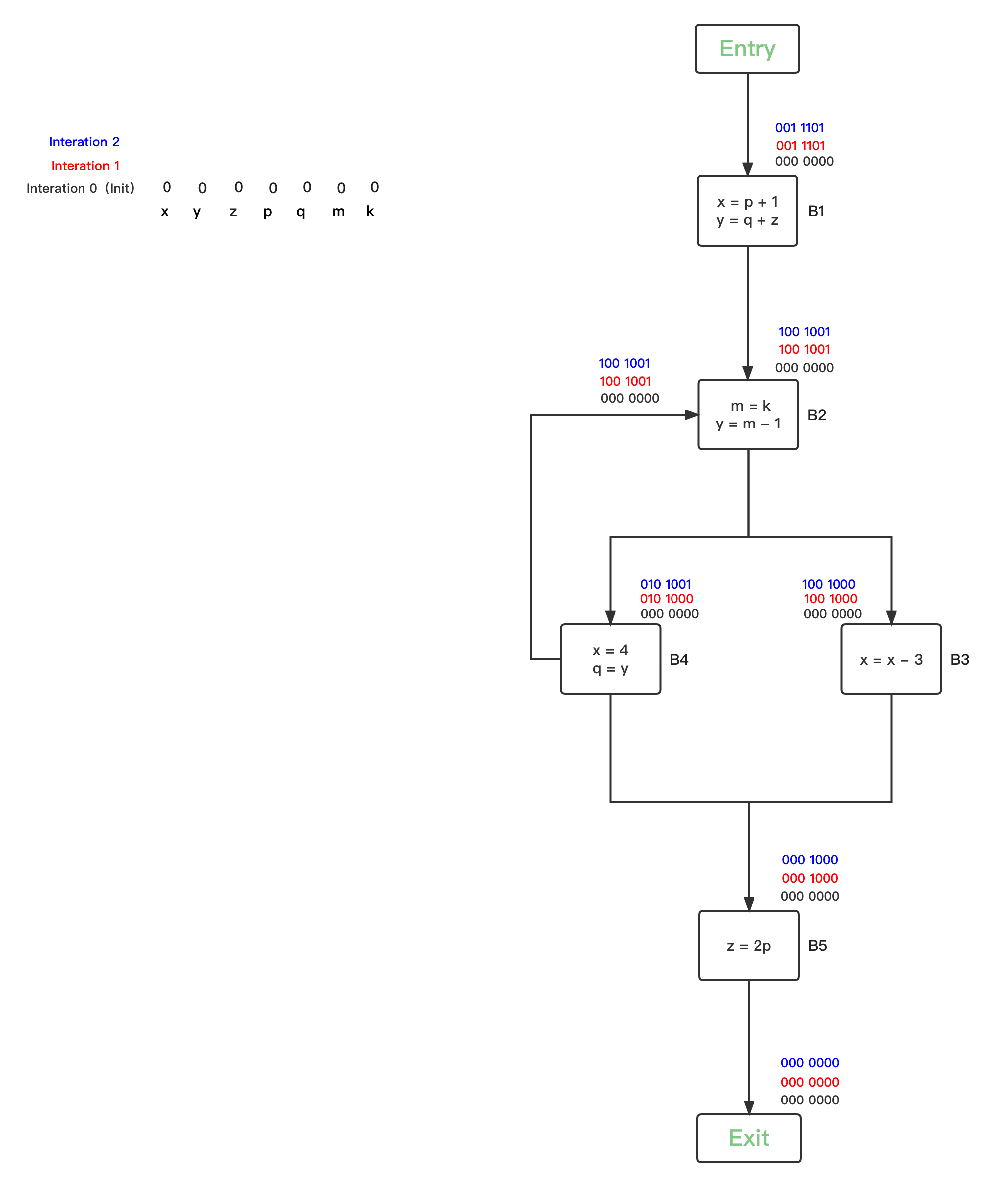
• 第四轮循环，统计上一轮发生OUT改变的的BBs有{B2、B3}，继续逐一safe-approximation分析：

• 第五轮循环，统计上一轮发生OUT改变的的BBs为空，分析结束：

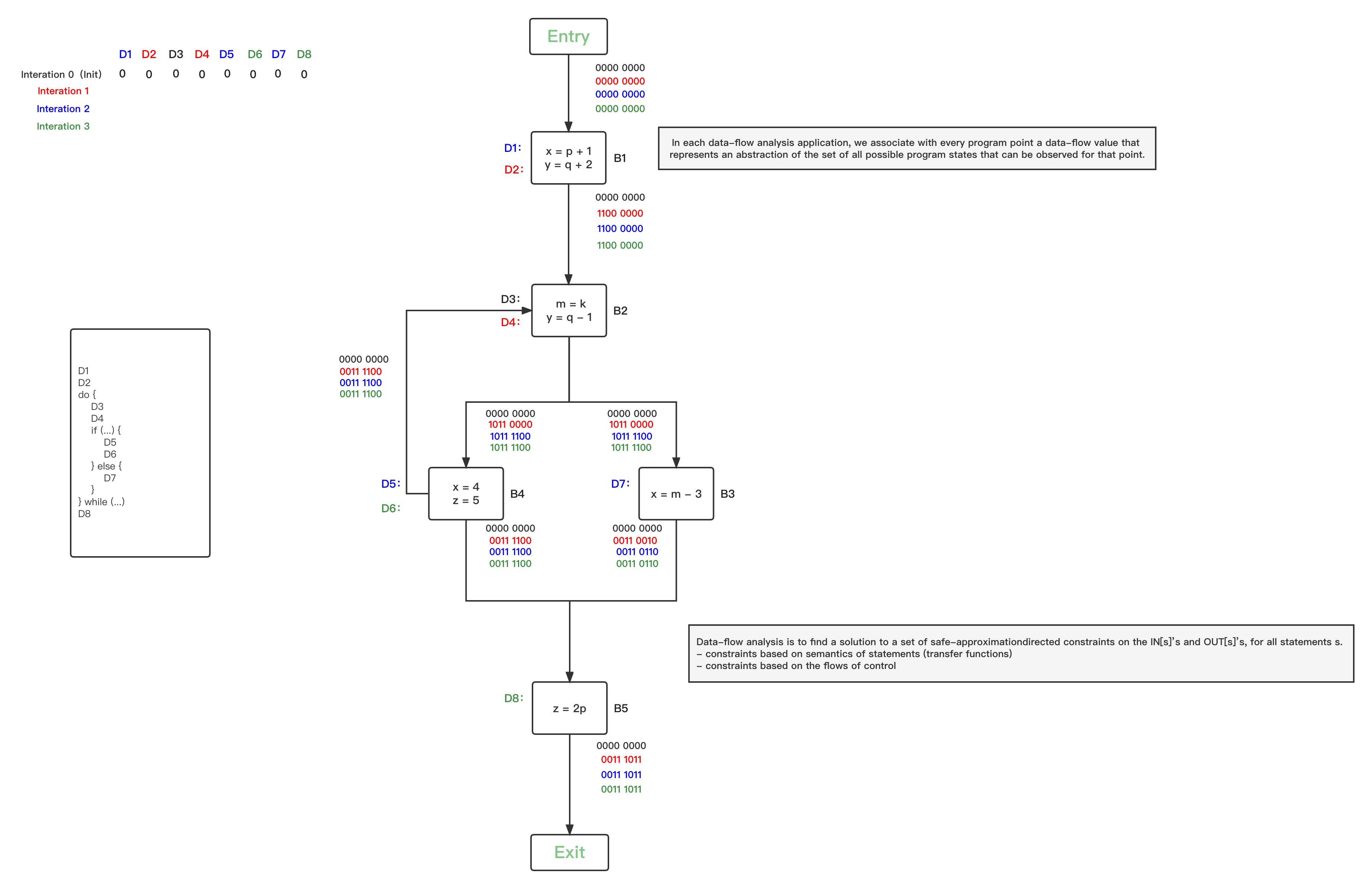
关于为什么RDA算法最后会收敛，只要记住以下几个核心关键点：

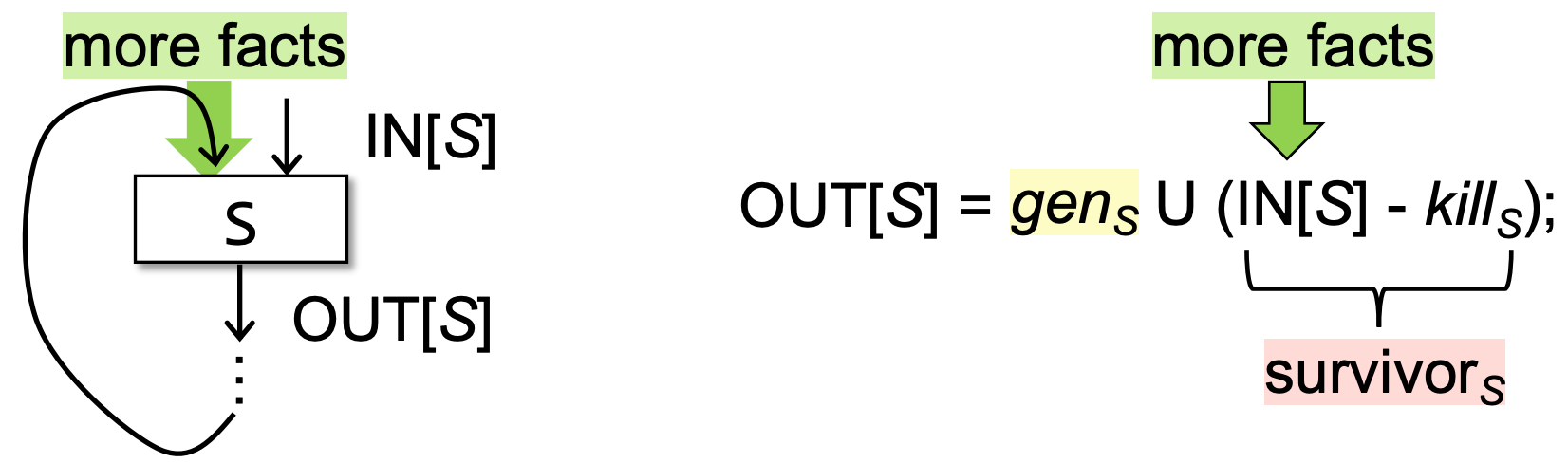
• gen_S and kill_S 是由程序结构决定的，保持不变：因为kill 与 gen 相关的 bit 是由程序代码决定的，不会因为 IN 的改变而发生改变。在每一轮循环中，gen_S and kill_S 像是信息发动机，不断给IN带来更多地信息。每一轮增加的bit facts由两部分组成
  • IN[S] - kill_S：survivor_S
  • gen_S
• 一旦一个fact bit被加入了OUT[S]，该bit就会永远留在OUT[S]中：因为在上一轮如果都没有kill掉该bit，在本轮以及之后的轮次也不是再被kill
• 如果IN's不发生改变，则OUT's也不会发生改变：此时该BBs收敛到一个fixed point（定点）
• OUT[S]的bits永远不会发生收缩：bits的状态变化只有3种情况（0->0、0->1、1->1）

  

四、Live Variables Analysis

基本概念

定义：Live variables analysis tells whether the value of variable v at program point p could be used along some path in CFG starting at p. If so, v is live at p; otherwise, v is dead at p.

• 考察变量 x 在程序点 p 上的值是否会在某条从 p 出发的路径中使用
  • 变量 x 在 p 上活跃，当且仅存在一条从 p 开始的路径，该路径的末端使用了 x，且路径上没有对 x进行覆盖
  • 反之
• 隐藏了这样一个含义：在被使用前，v 没有被重新定义过，即没有被 kill 过

该算法的应用场景有很多，例如：

1. 用于寄存器分配，当一个变量不会再被使用，那么此变量就可以从寄存器中腾空，用于新值的存储。 

活跃变量中的数据流值（Abstraction）

和Reaching Definitions针对每一个Definitions分配一个bit位不同，Live Variables Analysis给程序中的所有变量分配一个bit位，用 bit vector 来表示，每个 bit 代表一个变量。

活跃变量的转移方程和控制流处理（Safe-Approximation）

采用backward方式进行遍历分析，由每个节点自身的内部逻辑，决定其前驱的状态。 

• 一个基本块内，若 v = exp, 则 def v。若 exp = exp op v，那么 use v。一个变量要么是 use，要么是 def，根据 def 和 use 的先后顺序来决定。
• 考虑基本块 B 及其后继 S。若 S 中，变量 v 被使用，那么我们就把 v 放到 S 的 IN 中，交给 B 来分析，因此对于活跃变量分析，其控制流处理是 OUT[B] = IN[S]。
• 在一个块中，若变量 v 被使用，那么我们需要添加到我们的 IN 里。而如果 v 被定义，那么在其前驱的IN[B]语句中，v 是一个非活跃变量，即Dead了。
• 因此对于转移方程，IN 是从 OUT 中删去重新定值的变量，然后并上使用过的变量。需要注意，如果同一个块中，变量 v 的 def 先于 use ，那么实际上效果和没有 use 是一样的，因为def之后该变量就宣告dead了。

活跃变量的算法

我们用一个实际的例子来说明这个循环处理过程。

下图中，每一轮循环中，Live Variables bit vector的变化情况我们分别用不同的颜色表示，

• 第一轮循环，将所有BBs的IN[B]的live variables bit vector都初始化为0：

注意，因为考察的是IN[B]，所以我们将bit vector放在每个BBs的IN方向位置，从里到外排列。

• 第二轮循环，因为所有BBs的IN[B]的live variables bit vector都被初始化改变了，因此每一个BBs都要进行safe-approximation分析，从后往前进行Backward分析：

• 第三轮循环，统计上一轮发生IN改变的的BBs有{B1、B2、B3、B4、B5}，继续逐一safe-approximation分析：

• 第四轮循环，统计上一轮发生IN改变的的BBs有{B4}，继续逐一safe-approximation分析：

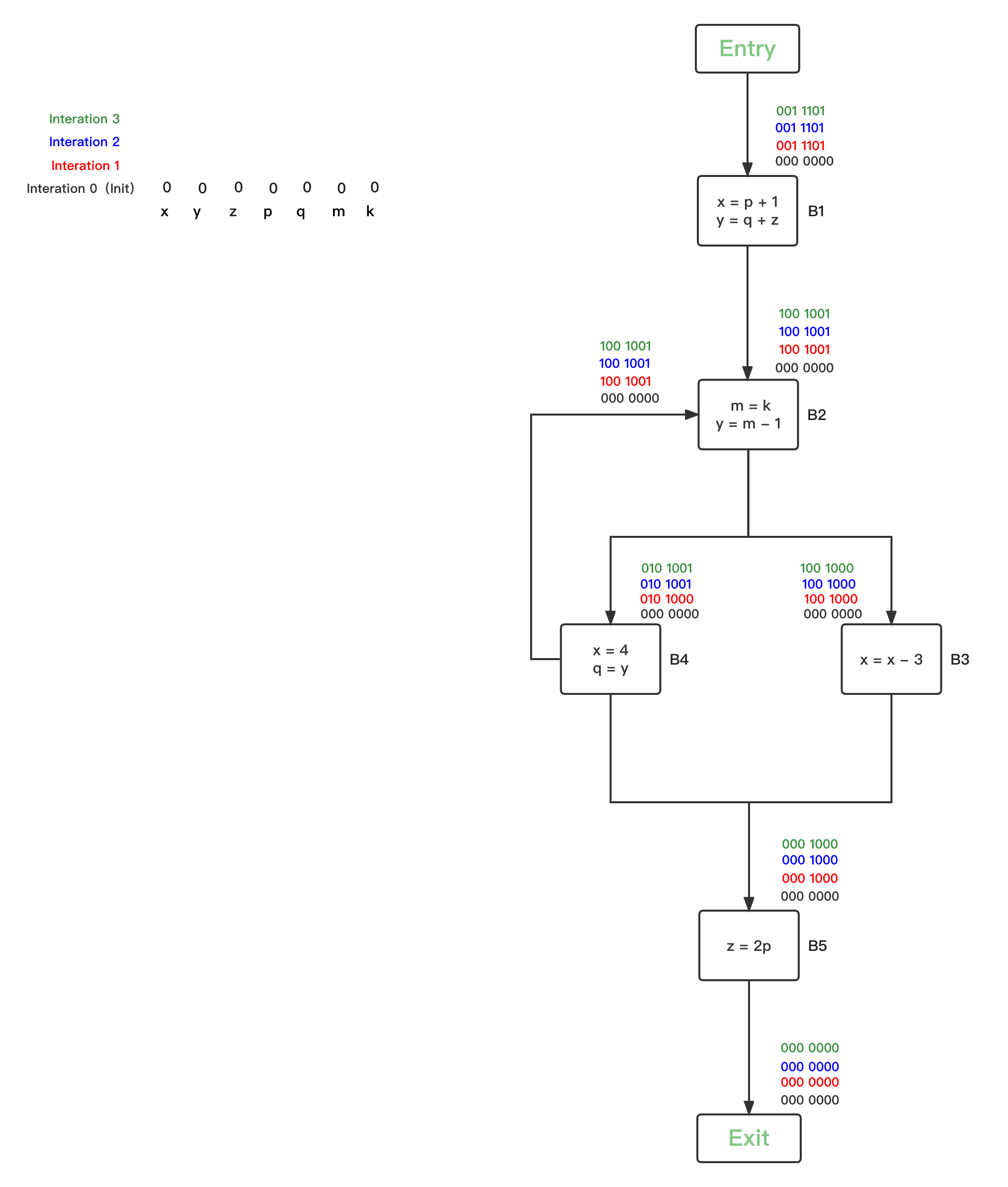
• 第五轮循环，统计上一轮发生IN改变的的BBs为空，分析结束 

 

五、Available Expressions Analysis

基本概念

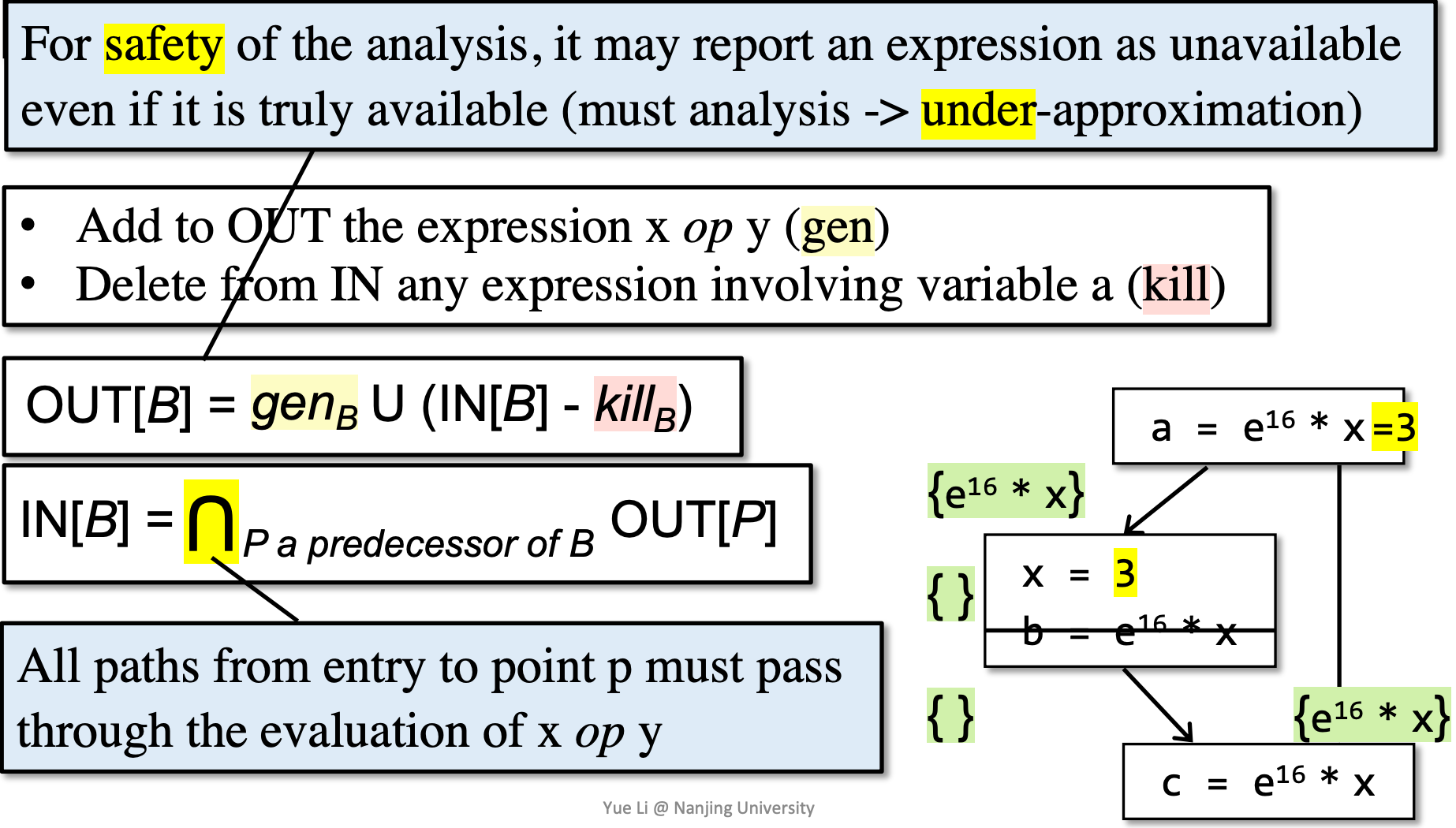
定义：An expression x op y is available at program point p if (1) all paths from the entry to p must pass through the evaluation of x op y, and (2) after the last evaluation of x op y, there is no redefinition of x or y. 

• x + y 在 p 点可用的条件：从流图入口结点到达 p 的每条路径都对 x + y 求了值，且在最后一次求值之后再没有对 x 或 y 赋值

算法应用场景：

• This definition means at program p, we can replace expression x op y by the result of its last evaluation
• The information of available expressions can be used for detecting global common subexpressions.

可用表达式可以用于全局公共子表达式的计算。也就是说，如果一个表达式上次计算的值到这次仍然可用，我们就能直接利用其中值，而不用进行再次的计算。

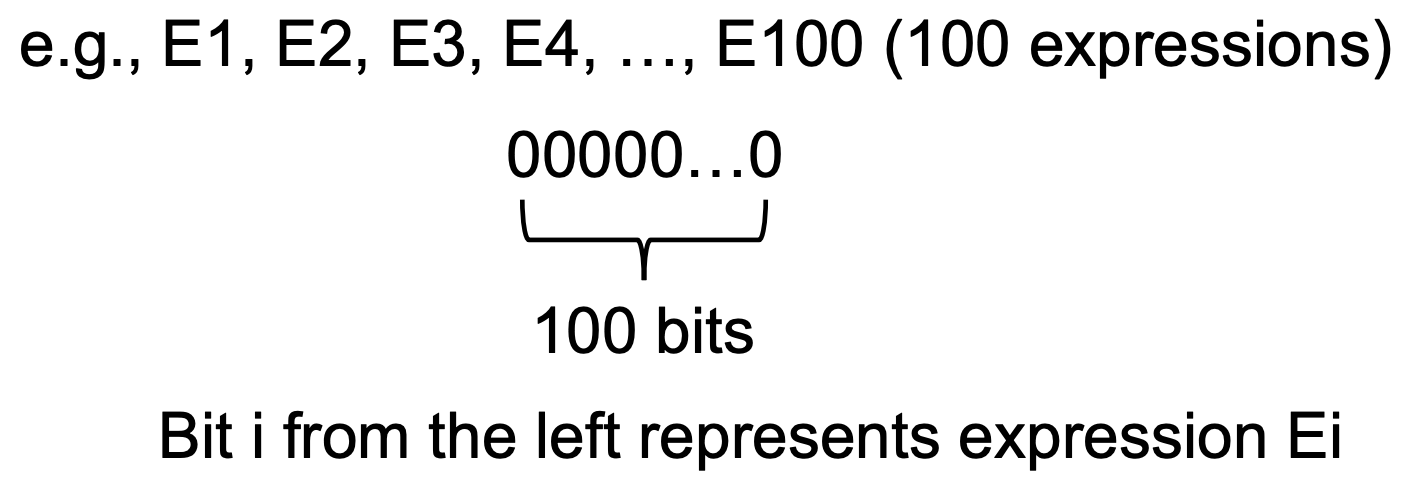
Available Expressions Analysis中的数据流值（Abstraction）

对程序中所有的expressions进行抽象，使用一个bit vectors进行表示，

Available Expressions的转移方程和控制流处理（Safe-Approximation）

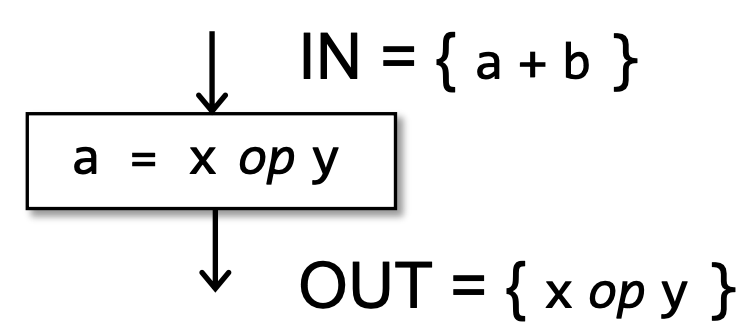
• 我们要求无论从哪条路径到达 B，表达式都应该已经计算，才能将其视为可用表达式，因此这是一个 must analysis。
• 注意到图中，两条不同的路径可能会导致表达式的结果最终不一致。但是我们只关心它的值能不能够再被重复利用，因此可以认为表达式可用。
• v = x op y，则 gen x op y。当 x = a op b，则任何包含 x 的表达式都被 kill 掉。若 gen 和 kill 同时存在，那么以最后一个操作为准。
• 转移方程到达定值的原理类似。但是，由于我们是 must analysis，因此控制流处理是取交集，而非到达定值那样取并集。

这里注意一点，如果可用表达式用于全局公共子表达式的计算。也就是说，如果一个表达式上次计算的值到这次仍然可用，我们就能直接利用其中值，而不用进行再次的计算，这是在编译器优化任务中很常见。在这个场景下，就必须使用must-analyzes，即要求每一条路径中，表达式都已经被计算且没有被重新定义。

因为在实际动态运行中，程序可能走任意一条路径，静态分析器为了保证safety，即保证程序被优化后不能运行出错，所以必须进行must-analyzes，即under-approximation analyzes。

Available Expressions的算法 

• 注意此时的初始化：一开始确实无任何表达式可用，因此OUT[entry]被初始化为空集是自然的。但是，其它基本块的 OUT 被初始化为全集，这是因为当 CFG 存在环时，一个空的初始化值，会让取交集阶段直接把第一次迭代的 IN 设置成 0，无法进行正确的判定了。
• 如果一个表达式从来都不可用，那么OUT[entry]的全 0 值会通过交操作将其置为 0，因此不用担心初始化为全 1 会否导致算法不正确。

我们用一个实际的例子来说明这个循环处理过程。

下图中，每一轮循环中，Available Expressions bit vector的变化情况我们分别用不同的颜色表示，

• 第一轮循环，将入口节点的OUT初始为0，所有BBs的Available Expressions bit vector都初始化为1：
• 第二轮循环，因为所有的BBs的Available Expressions bit vector都被初始化改变了，因此每一个BBs都要进行safe-approximation分析：

• 第三轮循环，统计上一轮发生IN改变的的BBs有{B1、B2、B3、B4、B5}，继续逐一safe-approximation分析：

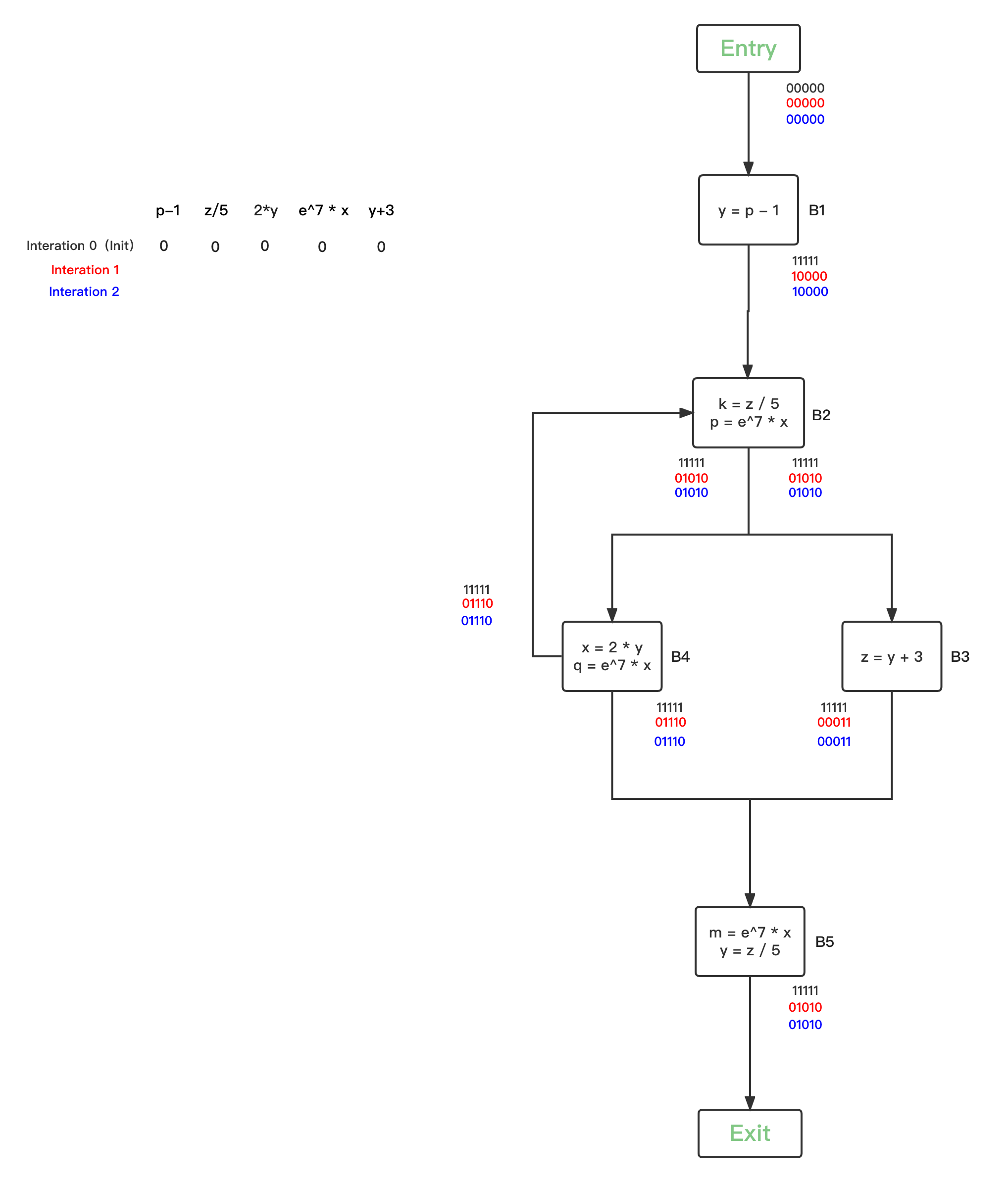
• 第四轮循环，统计上一轮发生OUT改变的的BBs为空，分析结束 

 

六、算法比较