ANSYS 粘弹性静力学仿真操作

前言

该文还有许多细节没有记录，挖坑待填~~

2023-3-7注：小小填补一部分

单元-材料-建模

• 单元类型 plane 182，option 中选择 plane strain or plane stress
• 材料属性有三种定义方式，使用 prony 级数更方便结合公式理解。ANSYS中体积模量和剪切模量的prony级数定义如下

\[K(t) = K_0 [\alpha_\infin^K + \sum^{n_K}_{i=1}\alpha_i^K exp(-\frac{t}{\tau_i^K})] \\ G(t) = G_0 [\alpha_\infin^G + \sum^{n_G}_{i=1}\alpha_i^G exp(-\frac{t}{\tau_i^G})] \]

ANSYS 使用相对模量 \(\alpha_i^K\) 和 \(\alpha_i^G\) 表示应力松弛，根据瞬时(instantaneous)模量 \(K_0\) 和 \(G_0\) 来比例放缩力学行为，其中 \(K_i = K_0 \alpha_i^K\) 在ANSYS内部进行计算。根据 \(K_0=K(0)\)，\(G_0=G(0)\) 计算出 \(t=0\) 时的弹性模量 \(E\) 和泊松比 \(v\)：

\[E = \frac{9K(0)G(0)}{3K(0)+G(0)}, \ v= \frac{3K(0)-2G(0)}{6K(0)+2G(0)} \]

操作实例：粘弹性材料的 prony 级数

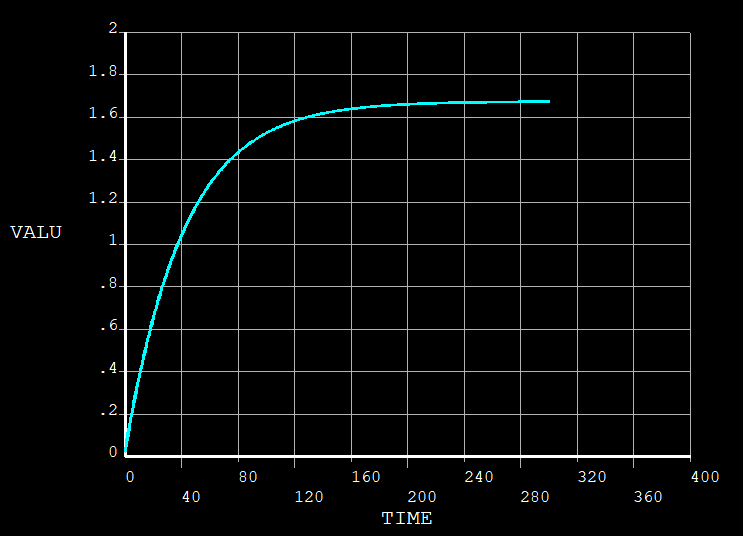
\[K(t) = 20000 \\ G(t) = 100 + 9900 \text{exp}(-\frac{t}{0.417}) = 1 \times 10^4[0.01 + 0.99 \text{exp}(-\frac{t}{0.417}] \]

得到

\[E = \frac{9 \times 2 \times 1}{3 \times 2 + 1} \times 10^4 = 25714.29\\ v = \frac{3 \times 2 - 2 \times 1}{6 \times 2 + 2 \times 1} = 0.28571 \]

在 ANSYS 中输入相关参数完成材料属性定义

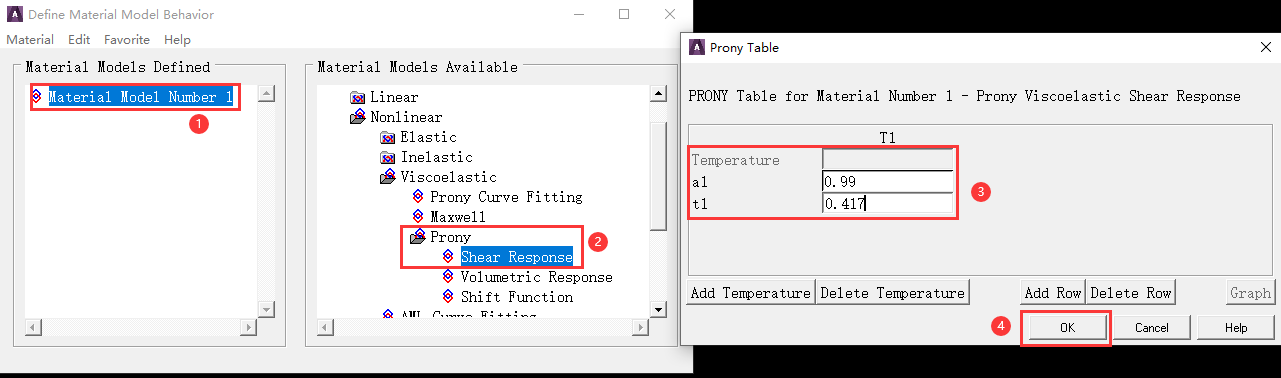
• step 1. 定义剪切模量的 Prony 系数
  
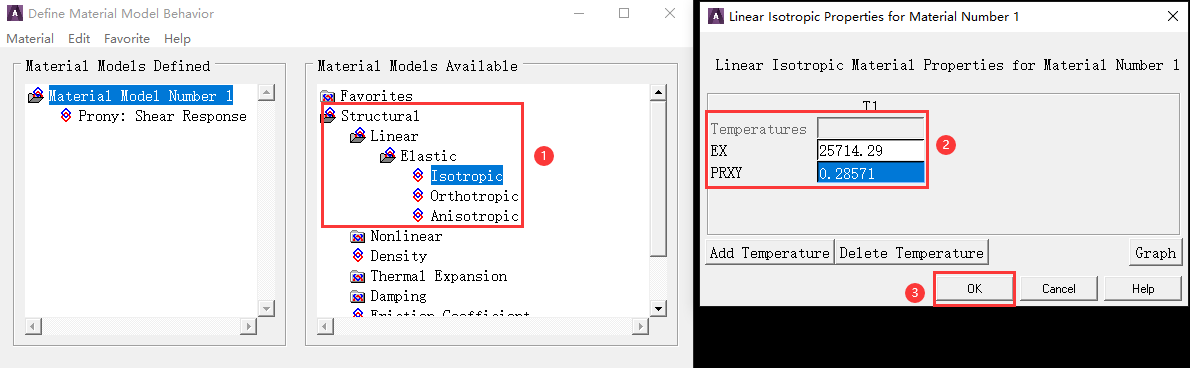
• step 2. 定义瞬时弹性系数
  

如何定义材料：The relaxation moduli at \(t=0\) are obtained from the elasticity parameters input using the MP command or via an elastic data table (TB,ELASTIC). The Prony series relative moduli and relaxation times are input via a Prony data table (TB,PRONY), and separate data tables are necessary for specifying the bulk and shear Prony parameters.

• 建模操作暂不做介绍

静力学分析 - static structural analysis

A static structural analysis determines the displacements, stresses, strains, and forces in structures or components caused by loads that do not induce significant inertia and damping effects. Steady loading and response conditions are assumed; that is, the loads and the structure's response are assumed to vary slowly with respect to time.

参考资料

---

[1] ANSYS帮助文档 - Mechanical APDL - Material Reference - 4.Nonlinear Material Properties - 4.7 Viscoelasticity.

---

---

最后更新于 2023年3月7日 --- 最初发表于 2023年2月3日
原创作者：LitBro
关于作者：继续狗刨~~
本文链接: [https://www.cnblogs.com/LitBro/p/17088651.html]
版权声明：本文采用 BY-NC-SA协议，转载或引用请注明出处!
关于后续：碍于学业不精，如有描述不当，还请见谅并非常感谢指出