MFEM库中NURBS网格文件格式记录
前言，这里有关于有限元开源软件包的介绍。我最近打算学习使用 MFEM 中提供的 IGA 做一些工作，官方文档关于 NURBS 网格文件的介绍不是特别细致，我在这里做一些理解补充
9-30 打开 MOOSE 官网一看，居然也支持 IGA 了！
Straight meshes
MFEM mesh v1.0
# Space dimension: 2 or 3
dimension
<dimension>
# Mesh elements, e.g. tetrahedrons (4)
elements
<number of elements>
<element attribute> <geometry type> <vertex index 1> ... <vertex index m> ...
# Mesh faces/edges on the boundary, e.g. triangles (2)
boundary
<number of boundary elements>
<boundary element attribute> <geometry type> <vertex index 1> ... <vertex index m> ...
# Vertex coordinates
vertices
<number of vertices>
<vdim>
<coordinate 1> ... <coordinate <vdim>> ...
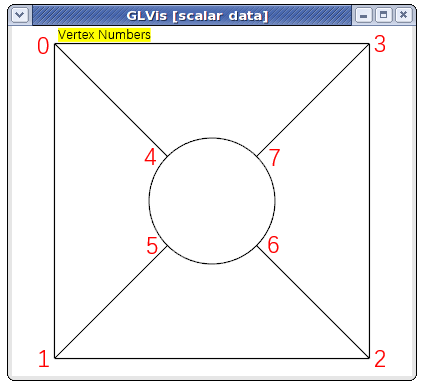
NURBS mesh，带孔方板
示意图：
现在根据模型解析出 网格文件 的格式，注释用 # 标识
MFEM NURBS mesh v1.0
#
# MFEM Geometry Types (see mesh/geom.hpp):
#
# SEGMENT = 1
# SQUARE = 3
# CUBE = 5
#
# Types of domains for integration rules and reference finite elements:
# Geometry::POINT - a point
# Geometry::SEGMENT - the interval [0,1]
# Geometry::TRIANGLE - triangle with vertices (0,0), (1,0), (0,1)
# Geometry::SQUARE - the unit square (0,1)x(0,1)
# Geometry::TETRAHEDRON - w/ vert. (0,0,0),(1,0,0),(0,1,0),(0,0,1)
# Geometry::CUBE - the unit cube
# Geometry::PRISM - w/ vert. (0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,0,1),(0,1,1)
# Geometry::PYRAMID - w/ vert. (0,0,0),(1,0,0),(1,1,0),(0,1,0),(0,0,1)
dimension
2
elements # 对应 NURBS patch
4
1 3 0 1 5 4 # 1-element attribute 3-geometry type {0 1 5 4}-vertex number
1 3 1 2 6 5 # 1-element attribute 3-square {1 2 6 5}-vertex number
1 3 2 3 7 6
1 3 3 0 4 7
boundary # NURBS 边界
8
1 1 0 1 # 1-boundary element attribute 1-geometry type {0 1}-vertex number
1 1 1 2 # 1-boundary element attribute 1-segment {1 2}-vertex number
1 1 2 3
1 1 3 0
1 1 5 4
1 1 6 5
1 1 7 6
1 1 4 7
edges
12
0 0 1 # 0-knotvector id {0 1}-vertex number
0 4 5
1 1 2
1 5 6
2 2 3
2 6 7
3 3 0
3 7 4
4 0 4 # 4-knotvector id {0 4}-vertex number
4 1 5
4 2 6
4 3 7
vertices
8
knotvectors
5
2 3 0 0 0 1 1 1 # 2-degree 3-control point number {0 0 0 1 1 1}-knot vector
2 3 0 0 0 1 1 1
2 3 0 0 0 1 1 1
2 3 0 0 0 1 1 1
2 3 0 0 0 1 1 1
weights
1
1
1
1
1
1
1
1
1
0.707106781
1
0.707106781
1
0.707106781
1
0.707106781
1
1
1
1
0.853553391
0.853553391
0.853553391
0.853553391
FiniteElementSpace
FiniteElementCollection: NURBS2
VDim: 2
Ordering: 1
0 0
1 0
1 1
0 1
0.358578644 0.358578644
0.641421356 0.358578644
0.641421356 0.641421356
0.358578644 0.641421356
0.5 0
0.5 0.217157288
1 0.5
0.782842712 0.5
0.5 1
0.5 0.782842712
0 0.5
0.217157288 0.5
0.15 0.15
0.85 0.15
0.85 0.85
0.15 0.85
0.5 0.108578644
0.891421356 0.5
0.5 0.891421356
0.108578644 0.5
我的其他相关博文
最后更新于 2022年4月21日 --- 最初发表于 2022年4月21日
原创作者：LitBro
关于作者：知识付费，shit!
本文链接: [https://www.cnblogs.com/LitBro/p/16171722.html]
版权声明：本文采用 BY-NC-SA协议，转载或引用请注明出处!
关于后续：碍于学业不精，如有描述不当，还请见谅并非常感谢指出
