线性方程组求解的投影方法介绍 - Projection Method

趁着还没忘，赶紧记录一下我对projection method的理解

考虑线性方程组

\[Ax=b \]

这里 \(A \in \mathbb{R}^{n \times n}\)，\(x\) 为变量，\(b\) 为右端项(right hand side, RHS)。投影法的概念是从 \(\mathbb{R}^n\) 的（搜索）子空间\(\mathcal{K}\) (subspace of candidate approximate)中得到近似解，若该子空间的维度为\(m\)，那么还得补充 \(m\) 个约束（可以想想约束的作用）。约束一般定义为与残差向量 \(b-Ax\) 正交的\(m\)个线性独立的向量。这些约束向量构成了维度为\(m\)的约束空间 \(\mathcal{L}\) (subspace of constraints)。

投影法分为正交(orthogonal)投影和斜(oblique)投影，区别在于解子空间 \(\mathcal{K}\) 和残差子空间 \(\mathcal{L}\) 的选取，正交投影： \(\mathcal{K}=\mathcal{L}\)，斜投影中 \(\mathcal{K}\) 不等于 \(\mathcal{L}\)，甚至毫无关系。

投影法的计算策略：

\[\text{Find } \hat{x} \in \mathcal{K}, \quad \text{such that} \quad b-A\hat{x} \perp \mathcal{L} \]

一般迭代求解的启动需要初始值\(x_0\)，此时近似解在仿射空间\(x_0+\mathcal{K}\)中寻找，即：

\[\text{Find } \hat{x} \in x_0+\mathcal{K}, \quad \text{such that} \quad b-A\hat{x} \perp \mathcal{L} \]

假设近似解为 \(\hat{x} = x_0 + \delta\)，初始残差向量为：

\[r_0 = b - A x_0 \]

因此

\[b - A\hat{x} = r_0 - A\delta \perp \mathcal{L} \]

换而言之

\[\hat{x} = x_0 + \delta, \quad \delta \in \mathcal{K} \\(r_0 - A\delta, w) = 0, \quad \forall w \in \mathcal{L} \]

上述的正交条件用图解释为：

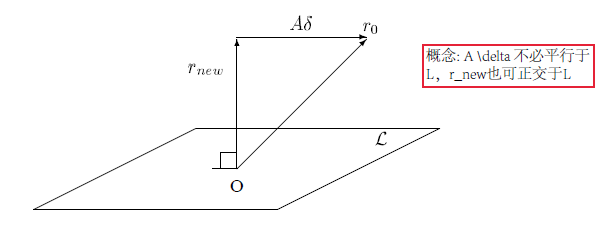
我的理解：对于定义的空间 \(\mathcal{K}\) 和 \(\mathcal{L}\)，以及初始值 \(x_0\)，初始值产生的残差向量为 \(b-Ax_0\)，现在需要想办法将残差向量的长度（2-范数）降低到一定程度。在原解空间中搜索近似解过于复杂，转而在子空间 \(\mathcal{K}\) 得到校正值 \(\delta\)，使得 \(\hat{x} = x_0 + \delta\) 产生的残差向量在空间 \(\mathcal{L}\) 上的投影长度为0，也相当于残差空间的某 \(m\) 个独立方向上的残差分量降为0。然后更新子空间 \(\mathcal{K}\) 和 \(\mathcal{L}\)，消除另外 \(m\) 个方向上的残差，到达一定水平后结束搜索，最终近似解为：\(\widetilde{x} = x_0 + \delta_1 + \delta_2 + ... + \delta_n \ (\delta_i \in \mathcal{L}_i)\)

另，对于斜投影有结论：一次投影步骤完成后，残差向量的2-norm不会超出初始残差向量的2-norm，即

\[\|r\|_2 \leq \|r_0\|_2 \]

而正交投影的收敛性结论就不一样

---

---

最后更新于 2022年2月13日 --- 最初发表于 2022年2月13日
原创作者：LitBro
关于作者：天！2022年了！
本文链接: [https://www.cnblogs.com/LitBro/p/15890829.html]
版权声明：本文采用 BY-NC-SA协议，转载或引用请注明出处!
关于后续：碍于学业不精，如有描述不当，还请见谅并非常感谢指出