有限元中等效结点力的一点理解

前段时间想给算例加一种边界条件，想着想着，发现写的有限元程序适配度不够高，得小小改动一下。

改着改着又发现关于等效结点力我好像一直没理解透，只知道有这个东西，但是不清楚具体来历，还是老老实实整理一下吧。

首先让我们请出有限元 [👏]，考虑弹性力学平面问题的有限元推导，用的最小势（位）能原理，得到势能泛函：

\[\Pi = \int_{\Omega} \frac{1}{2} [\epsilon]^T [D] [\epsilon] t \mathrm{d}x \mathrm{d}y - \int_{\Omega} [u]^T [f] t \mathrm{d}x \mathrm{d}y - \int_{\Gamma} [u]^T [T] t \mathrm{d}\Gamma \]

其中，\([\epsilon]\) 为应变，\([D]\) 为弹性矩阵，\(t\) 为二维体厚度， \([u]\) 为位移，\([f]\) 为体积力，\([T]\) 为面力。对于有限元离散模型，系统的势能是各个单元势能之和，因此得到：

\[\Pi =\sum\Pi^e=\sum\{ [a^e]^T\int_{\Omega_e} \frac{1}{2} [B]^T [D] [B] t \mathrm{d}x \mathrm{d}y [a^e] - [a^e]^T \int_{\Omega_e} [N]^T [f] t \mathrm{d}x \mathrm{d}y - [a^e]^T \int_{\Gamma_e} [N]^T [T] t \mathrm{d}\Gamma \} \]

其中，\([a^e]\) 为单元结点位移向量 ， \([B]\) 为单元应变矩阵，\([N]\) 为单元形函数列阵。这两公式摆出来有点劝退，😱，顶住。

---

我们暂时先忽略体积力哈，单元等效结点载荷列阵就藏在上边，我们把它揪出来：

\[[P^e] =\int_{\Gamma_e} [N]^T [T] t \mathrm{d}\Gamma \]

为什么是说是等效呢？因为 \([a^e]^T[P^e]\) 的物理意义就是 【等效的】外载荷 \([T]\) 在边界位移 \([u]\) 下的势能。

【力*位移】得到的是关于能量的一个值嘛，前面也说了，\([a^e]\) 是结点位移，\([P^e]\) 是定义的等效结点力，作用在结点上（这里只是假设的，其实并没有一个这样的力存在）。

这样原本一个面上的面力（外载荷）在这个面的位移下的势能，写成了，面上每个结点的位移乘上对应的等效结点力，这便是等效结点力的物理意义了。

---

现在来到实操部分，理论有了，实际程序该怎么算呢？

书上有个关于三角形单元，一边均布面力的等效结点力计算，截图如下：

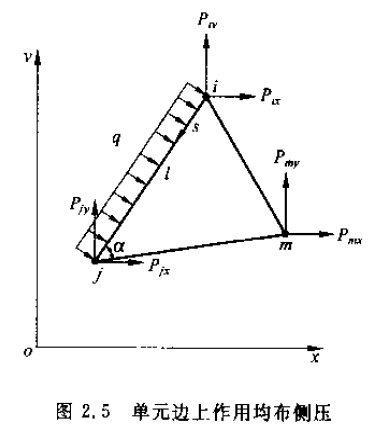
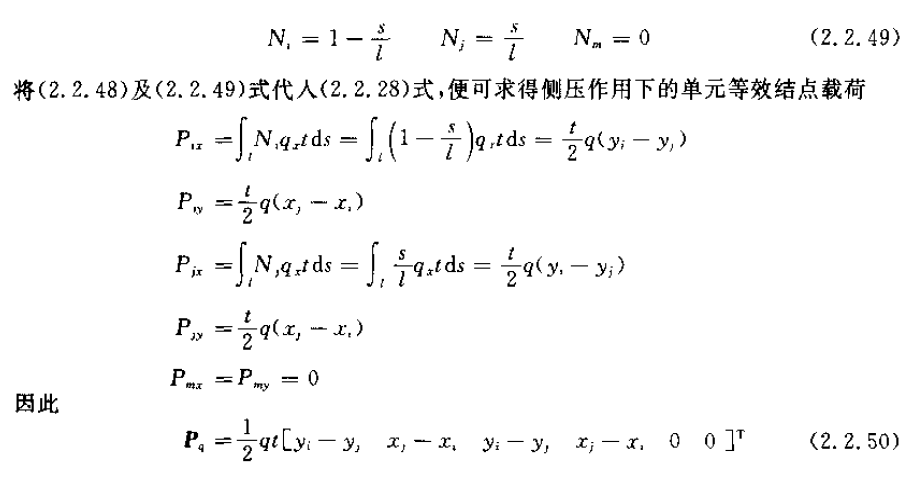
我们发现，原本好端端的形函数 \([N]\)，这里怎么变身了呢？冷静，肯定有猫腻！

如 2.2.49 式，形函数已经转换到了局部坐标系，关于面力施加的那个面的一个坐标系，再仔细打量打量，咦，这不和两点线性插值公式一样嘛！

由以前所学的知识，我们知道，三角形单元是个常应变单元，位移模式是线性的，这里就把这个线性的概念用上，狠狠发挥了一波。

因此，在那条载荷边上，结点 \(i,j\) 位移已知的话，这边上的 x 方向位移就会是这样变化的：

\[u_x|_\Gamma = N_i*u_{ix} + N_j*u_{jx} + N_m*u_{mx} \\ =(1-\frac{s}{l})u_{ix} + \frac{s}{l}u_{jx} \]

好了，现在，这一切都可以解释通了。换一种思路，三角形单元 x 位移场写成如下：

\[u_x = N_i(x,y)*u_{ix} + N_j(x,y)*u_{jx} + N_m(x,y)*u_{mx} \]

当 \((x,y) \in \Gamma\) 时，

\[u_x(x,y) = u_x|\Gamma \]

嗯，就是这样了，对于四边形单元，求等效结点力的时候考虑积分区间，结果很容易就计算出来了。

从这抄的

---

[1] 王勖成. 有限单元法, 清华大学出版社, 北京, 2003.

---

---

最后更新于 2021年1月25日 --- 最初发表于 2021年1月25日
原创作者：LitBro
关于作者：咕咕咕
本文链接: [https://www.cnblogs.com/LitBro/p/14326008.html]
版权声明：本文采用 BY-NC-SA协议，转载或引用请注明出处!
关于后续：碍于学业不精，如有描述不当，还请见谅并非常感谢指出