有限胞元法 --- Finite Cell Method

（5月有点忙，先蹲个坑位，原本想写的，资料太杂且大多在学校，论文还得弄，秃，还没整理）

6月... 咕...
我好懒...

Intro#

对复杂模型进行有限元分析都离不开网格的剖分，这通常会占据很大一部分工作量，并且网格的优劣对求解精度也有一定影响。因此，如何简化网格剖分的同时保证精度非常有必要研究。这时有限胞元法（FCM，Finite Cell Method，中文译名引自论文[1]）的提出可以解决一般有限元法的网格适应性问题。

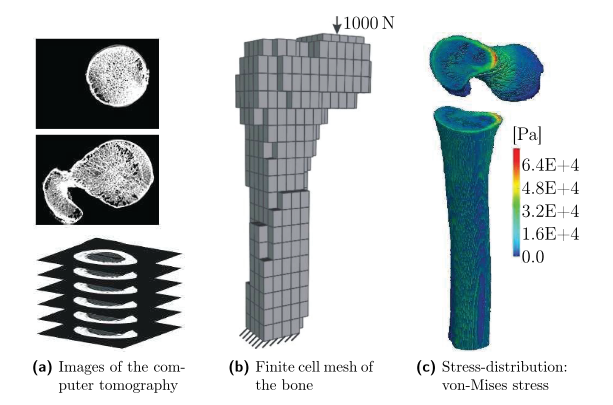
基本线路：FCM将不规则物理域 $\Omega$ 拓展为一个规则域$\Omega_{em}$，拓展的域$\Omega _{fict}$被称作虚拟域。类似level set的思想，将会引入一个参数$\alpha$，域内为1，域外为0。

对这个规则域进行离散就非常方便了，现有离散方式如下：

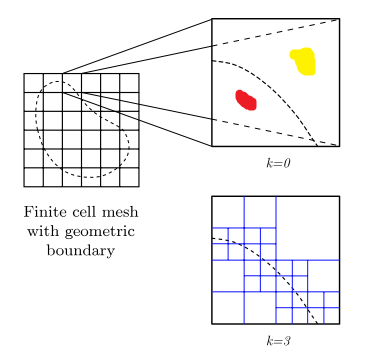
假如一个单元完全在物理域中，计算方式和一般有限元一致，假如一个单元完全在虚拟域中，计算方式也和一般有限元一致。最后需要将这两种单元的系数矩阵乘以系数$\alpha$再进行整体系数矩阵的组装。

假如一个单元（Cell）一部分在物理域中，一部分在虚拟域中，这时候就需要特殊的处理方式。如上图，红块所在区域为物理域，黄色所在区域为虚拟域。对这个边界胞元求解系数矩阵时，由于场函数在这个单元内不连续，不能使用标准高斯积分来近似求解。这时候一种近似求解方法就是将这个胞元进行分块，每个块都是一个积分域，同样都需要乘系数$\alpha$。每个子积分域内进行复合高斯积分，将得到的结果组装就得到了这个边界胞元的系数矩阵。

在有限元中，提高计算精度通常有两种方法，h-method和p-method，一是增加网格密度，一是提高试函数阶次。在FCM中，一般使用p-method来提高求解精度，这样边界胞元的复合高斯积分也会更加准确。

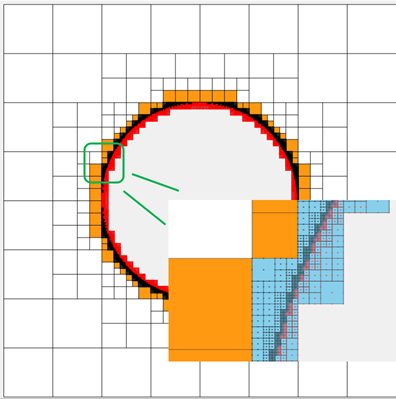
例子：蓝色为边界胞元，胞元进行了3次划分（四叉树），胞元中红点和黑点为高斯积分点

参考文献#

---

[1] 赵林英. 基于固定网格的形状\拓扑优化新方法研究 [D]. 西安: 西北工业大学, 2017.

---

---

最后更新于 2020年8月2日 --- 最初发表于 2020年8月2日
原创作者：LitBro
关于作者：咕咕咕
本文链接: [https://www.cnblogs.com/LitBro/p/13021979.html]
版权声明：本文采用 BY-NC-SA协议，转载或引用请注明出处!
关于后续：碍于学业不精，如有描述不当，还请见谅并非常感谢指出