反问题与正则化
不适定的反问题
在学习过程中,涉及到了数学物理中的反演问题,【正问题】一般可简化为输入,输出和转换系统,即
其中,\(\mathbf{F}\) 表示转换关系(一般为算子或积分,已知),\(x\) 为输入参数,\(y\) 为输出数据,\(\mathbf{X}\) 和 \(\mathbf{Y}\) 为对应的赋范空间。从【反问题】的角度来考虑,求解问题变为
即已知输出数据,反求出输入参数。经常说问题的适定性对求解存在很大的影响,先从适定性的定义出发,假设问题\(\eqref{eq2}\)是适定(well-posedness)的,则全部满足[1]:
- \(C_{1}\):\(\forall \ y \in \mathbf{Y}\),\(\exists \ x \in \mathbf{X}\),使得\(\eqref{eq2}\)成立;
- \(C_{2}\):\(\eqref{eq2}\)的解 \(x\) 是唯一的;
- \(C_{3}\):\(\eqref{eq2}\)的解 \(x\) 连续依赖于 \(y\)
要求问题\(\eqref{eq2}\)适定的条件下,等同于要求 \(\mathbf{F}^{-1}\) 存在且连续,然而很多问题都是不满足这个条件的,也就是说不适定 --- (如热传导问题中,对于给定的边界条件,能够得到唯一的一组温度数据;但是一组温度数据不一定对应唯一的一组边界条件)。
许多反问题都是不适定的,普遍存在 \(x\) 不连续依赖于 \(y\) ,并且 \(y\) 的微小扰动会使 \(x\) 产生剧烈波动的问题,也即病态问题,这时我们所求的反问题的解通常是最小二乘意义下的解 \(x^* \in \mathbf{X}\),即
注:不可将适定性与病态性视作一种概念,并且它们没有从属关系,要理解需从各自的定义出发,可大致参考[知乎],[Exchange]
病态(ill-conditioned)问题:当一个问题的输入受到微小的扰动即可引发输出解的剧烈变化时,也即问题的解对输入参数非常敏感,便称它是病态问题
反问题与不适定的联系主要表现在两个方面[2]:1、由于客观条件的限制,反问题中的数据往往是欠定或者过定的,这就导致解的不唯一性或者是解的不存在性;2、反问题的解对数据往往不具有连续依赖性,并且通常这种不连续这是导致反问题病态的原因。在\(\mathbf{F}^{-1}\) 的连续性不满足的情况下,即条件 \(C_3\) 不满足的情况,如何通过一组带有误差的数据稳定求出满足精度的结果,显然非常重要。
例1:考虑一个一维阶跃函数
\[{F}(x) = [x] \ (x \in R^1) \tag{4} \label{eq4} \]显然 \(\eqref{eq4}\) 并不连续,考虑 \({F}(3.001) = 3\) ,若存在误差 \(\delta\),\(3.001+\delta = 2.999\),那么 \({F}(2.999) = 2\),显然一个很小的误差 \(\delta = -0.002\) 对求解带来了很大的影响,这也表明问题 \(\eqref{eq4}\) 是病态的。
例1合理性待确定,想通过这例子直观的反映出我对这部分内容的理解,如有不合理处或更好的举例还望不吝指教
为获得最小二乘意义下的解 \(x^*\) ,需要利用一种算法来求解无约束最小化问题 \(\eqref{eq3}\) ,这些算法有:演化类算法,梯度类算法等。这些算法都用各自的搜索方法寻求目标函数的极小值,并且这些算法的搜索效率和准确度在应用中各有优劣。在存在测量误差的情况下,对于适定非病态问题,这些算法大都能很好的求解,但对于不适定病态问题,这些算法就无法足够稳定准确地求解,因此人们发展了正则化方法来处理这些不适定病态问题。
正则化
regularization: (n.) 规范化;正则;规则化;调整
正则化(regularization)这个名词听着总让人摸不着头脑,从中文词义上更是找不出含义。从英文名词的角度看,有添加约束,增加条件的含义。
在实际反问题中,由于测量误差的无法避免,精确数据 \(y\) 无法得到,只有包含误差的数据 \(y_{\delta} = y + \delta\) ,这时相当于求解问题:
然而这通常是不可解并且极不稳定的,同时 \(\mathbf{F}^{-1}\) 也不可求,因为包含误差的 \(y_{\delta}\) 很有可能不在空间 \(\mathbf{Y}\) 中,又或者解对输入数据非常敏感,使得 \(x_\delta\) 与精确解相差甚远,这时候构造一个正则算子 \(\mathbf{R}(\alpha)\) ,并且满足
这时
其中 \(x^{r}_{\delta}\) 表示误差数据 \(y_{\delta}\) 在正则算子下的解,并且 \(x^{r}_{\delta}\) 足够接近精确解 \(x\) 。其中 \(\alpha\) 与解的稳定性和准确性密切相关,一般来说 \(\alpha\) 越大稳定性越好,而 \(\alpha\) 越小解的准确度更高,因此选择一个依赖误差水平的正则化参数 \(\alpha(\delta)\) 来合适地平衡稳定性和准确性正是正则化的精妙所在。
例2:考虑一个 Heaviside 函数
\[H(x)= \begin{cases} 1 & x>0 \\ 0 & x \le 0 \end{cases} \tag{8} \label{eq8} \]与 \(\eqref{eq4}\) 性质类似,因此 \(\eqref{eq8}\) 还有一个正则化的形式
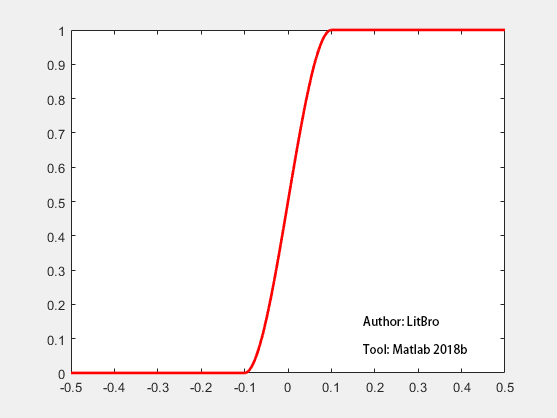
\[H_r(x)= \begin{cases} 1 & x>{\alpha} \\ -{\frac{3}{4}}({\frac{x}{\alpha}}-{\frac{x^3}{3\alpha^3}})+{\frac{1}{2}} & -\alpha \le x \le \alpha \\ 0 & x < -{\alpha} \end{cases} \tag{9} \label{eq9} \]函数图如下( 图中 \(\alpha = 0.1\) )
\(H(0.001)=1\) 加上误差后 \(H(-0.001)=0\) ,而 \(H_r(-0.001)=0.4925\) ,可以发现正则化后离精确解的准确度明显提高,并且准确度随着 \(\alpha\) 的减小而增加,相应的稳定性却降低了,反之同理。
通过例2可以看出,正则化在某种程度上可以看作是构造另外一个算子,与原算子性质大体一致,却更加稳定,光滑连续。
为不同的问题选择合适的正则化方法对求解也同样重要,即正则算子 \(\mathbf{R}(\alpha)\) 的选择。这里我只是具体化地阐述了正则化的概念,并没有具体到正则化方法的推导和使用,介绍正则化方法(如经典的Tikhonov正则化)也应该会在另一篇文章里头了吧。
参考文献
[1] 王彦飞. 反演问题的计算方法及其应用 [M]. 北京: 高等教育出版社, 2007.
[2] 郑恩希. 几种不适定问题的正则化方法及其数值实现 [D]. 吉林: 吉林大学, 2009.

最后更新于 2021年1月4日 --- 最初发表于 2020年4月20日
原创作者:LitBro
关于作者:咕咕咕
本文链接: [https://www.cnblogs.com/LitBro/p/12735745.html]
版权声明:本文采用 BY-NC-SA协议,转载或引用请注明出处!
关于后续:碍于学业不精,如有描述不当,还请见谅并非常感谢指出


 浙公网安备 33010602011771号
浙公网安备 33010602011771号