插值中节点和结点的区别
前言：我在学有限元（王勖成）和计算方法（王能超）时经常碰到这两个定义，有限元中单元上的插值点称作node（结点），而计算方法中的插值方法中称插值点为knot（节点）。明明都是对未知函数的一个插值近似，为什么插值点会有两种表示形式？ ('⊙д⊙) 很迷
ATTENTION：本文主体纯属搬运，夹杂部分自我理解，具体请以搬运为准，搬运来自StackExchange
带着这个疑问我试着在网上搜索了一下，看是否有人和我同样困惑，找到了如下内容：
问题标题
在插值中结点（nodes）与节点（knots）的区别是啥啊?
问题描述
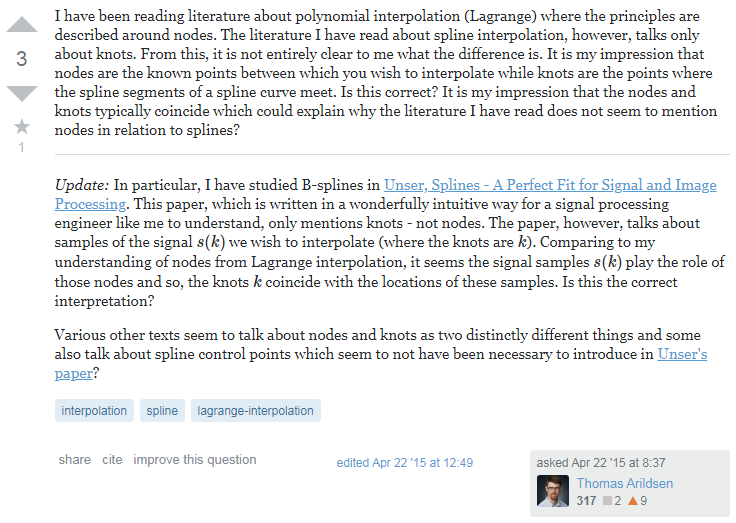
’我‘（不是我）读过一些关于多项式插值的文献，其中lagrange插值中插值的依据是结点（nodes），而样条插值中是节点（knots），这些说法对‘我’来说很不清晰。以‘我’的感觉来看：结点是一些你需要插值的多项式的已知内点，而节点是间断样条间的交接点。’我‘感觉在样条插值中结点与节点通常重合，这可以解释为什么在这些文献中没有提及到结点的说法。
问题解答
（此解释部分太过理论，这里就仅仅以我的理解进行二次解释吧）：
结点：选用多项式插值方法（例如： lagrange），一系列基函数的n个点的位置\(x\)（不重合,\(x_1,x_2,...,x_n\)）及对应结果\(k\)（可以任意,\(k_1,k_2,...,k_n\)）已知，你可以得到一个唯一的多项式\(F\)（次数小于\(n\)）：
这个的证明非常巧妙简单，详见[传送门]，在这个空间中，任意一组不重复的插值点都能对应一个唯一的结果，唯一性点集，这些点被称为结点（nodes），wiki中也是这么称呼的。
节点：相反的，在样条插值中，任意一组不重复的插值点也都能得到对应的插值结果，但插值结果还需满足额外的条件，如光滑性条件。即不同的条件能够得到不同的插值结果，不满足唯一性。因此这些点被称为节点（knots）。
最后更新于 2020年4月22日 --- 最初发表于 2019年12月21日
原创作者：LitBro
关于作者：咕咕咕
本文链接: [https://www.cnblogs.com/LitBro/p/12078130.html]
版权声明：本文采用 BY-NC-SA协议，转载或引用请注明出处!
关于后续：碍于学业不精，如有描述不当，还请见谅并非常感谢指出
