一.概述
首先我们先搞清楚什么最短路径树,我们这里可以引申三个概念,最短路径,最短路径树,最小生成树
最短路径:最短路径就是指两点之间的最短距离,通常算法有dij,spfa,floyed
最短路径树:概念就是以一个节点为根,然后根节点到其他所有点的距离最短,然后形成了一棵树,把不必要的边删除,其实我们用dij的时候求一个点到其他点的距离的时候就已经会把根节点到其他所有点的最短距离求出来了,只是我们不确定是哪些边构成的
最小生成树:没有根的概念,就是用最小的花费保证所有点直接或者间接联通
这里我来盗用大佬的图好理解一下
原图:
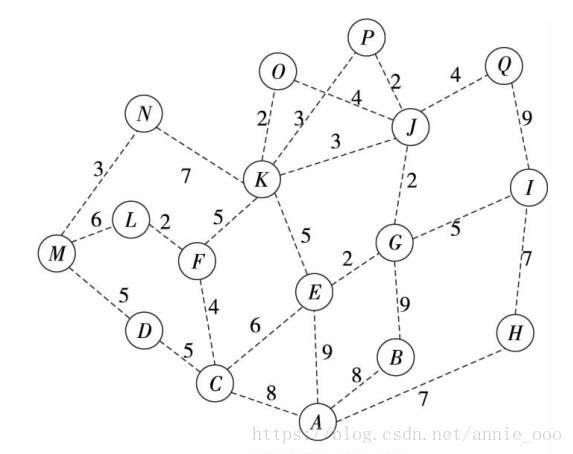
最短路径树 最小生成树
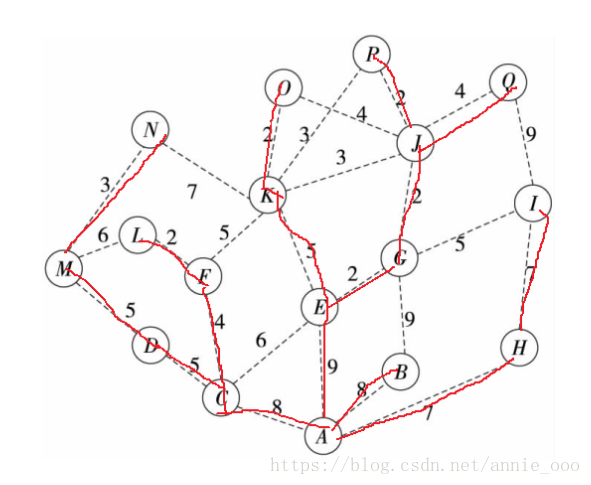
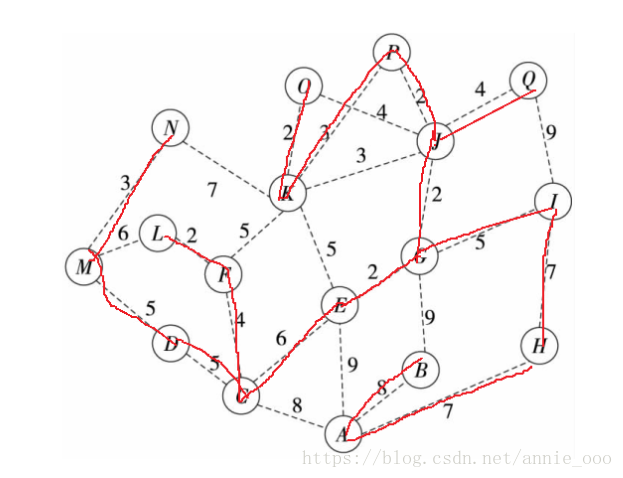
二.做法
我们一般可以怎么来写呢
第一种:我们用dij求出最短路径,我们已经知道建造整颗最短路径树的花费,然后我们去枚举每一条边,假设把这条边删掉,如果最小花费有影响,说明这个肯定是最短路径树上的边,相等的情况要处理一下,复杂度是O(nlogn*nlogn)
第二种:显然第一种复杂度太高了,一点都不现实,所以我们一般使用第二种方法,我们还是一样先求一遍dij,然后我们知道根节点到其他点的距离,我们dfs一遍,如果dis[v]=dis[u]+w,说明这条边可以充当最短路径树上的边,换上并且没有影响,或者我们直接枚举每一条边,判断这个条件也可以,看题目不同的需求下要处理什么
三.例题巩固
Description
n个城市用m条双向公路连接,使得任意两个城市都能直接或间接地连通。其中城市编号为1..n,公路编号为1..m。
任意个两个城市间的货物运输会选择最短路径,把这n*(n-1)条最短路径的和记为S。现在你来寻找关键公路r,公
路r必须满足:当r堵塞之后,S的值会变大(如果r堵塞后使得城市u和v不可达,则S为无穷大)。
Input
第1行包含两个整数n,m,
接下来的m行,每行用三个整数描述一条公路a,b,len(1<=a,b<=n),
表示城市a和城市b之间的公路长度为len,这些公路依次编号为1..m。
n<=100,1<=m<=3000,1<=len<=10000。
Output
从小到大输出关键公路的编号。
Sample Input
4 6
1 2 1
2 3 1
3 4 1
1 4 1
1 3 1
4 1 1
Sample Output
1
2
3
5
题意:这题很明显就是要求分别以n个节点为根时的最短路径树上的边不同的条数
思路:这个题我们使用第一种和第二种都可以,如果时上面的边我们vis数组标记一下,最后统一计数
[CH6202]黑暗城堡
题意:一个图,让你求以1为源点,所能求出的最短路径树有多少种不同的构造方法
思路:因为我们要保证到每个点的距离最小,所以我们其实只能用相同的权值替换当前最短路径树上的边,然后运用乘法原理相乘即可
BZOJ 4016
题目:https://vjudge.net/contest/307753#problem/F
题意:给你一个图,让你建一个最短路径字典序最小的树,然后在最短路径树上找节点数正好为k的最长路径长度,并且记录这样的路径数有多少条
思路:我们首先dij跑一遍,然后dfs按点从小到大就能跑出树来,然后其实树上路径操作就很明显是点分治了,我们在计算距离的时候我们就可以记录最长路径,相等则记录个数,有点树形DP模板的意思,详解看这篇点分治的讲解 https://www.cnblogs.com/Lis-/p/11359366.html

#include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #include<iostream> #include<vector> #include<queue> #define maxn 100005 #define mod 0x3f3f3f3f using namespace std; typedef long long ll; ll da; vector<pair<ll,ll> > mp[maxn],xx[maxn];//存下图 pair<ll,ll> e[maxn],e2[maxn],flag[maxn]; bool vis[maxn];//标记曾经使用过的重心 ll maxsize[maxn],dis[maxn],d[maxn];//maxsize 当前节点的最大子树 ll siz[maxn],xd[maxn];// dis 到重心的距离 d 出现过的距离 ll n,m,k,rt,sum,qe,qe2,ans1,ans2; // siz 当前节点的子树个数 e 出现的距离 rt代表当前重心 void find(ll x,ll f){//找出重心 siz[x]=1; maxsize[x]=0; for(int i=0;i<mp[x].size();i++){ pair<ll,ll> q=mp[x][i]; if(q.first==f||vis[q.first]) continue;//vis数组标记曾经使用过的重心 find(q.first,x); siz[x]+=siz[q.first]; maxsize[x]=max(maxsize[x],siz[q.first]); } maxsize[x]=max(maxsize[x],sum-siz[x]);//节点总数减去当前的子树数=以当前节点为根的父亲点子树数 if(maxsize[x]<maxsize[rt]){ rt=x; } } void query(ll z,ll sm){ if(z>ans1){ ans1=z; ans2=sm; } else if(z==ans1){ ans2+=sm; } } void get_dis(ll x,ll f,ll len,ll num){ e[qe].first=len; e[qe++].second=num; e2[qe2].first=len; e2[qe2++].second=num; if(num==k){ query(len,1); } ll t=k-num+1; if(flag[t].second){ query(flag[t].first+len,flag[t].second); } for(int i=0;i<mp[x].size();i++){ pair<ll,ll> q=mp[x][i]; if(q.first==f||vis[q.first]) continue; dis[q.first]=dis[x]+len; get_dis(q.first,x,len+q.second,num+1); } } void divide(ll x){ vis[x]=1; //printf("rt=%lld ans1=%lld ans2=%lld\n",x,ans1,ans2); qe2=0; for(int i=0;i<mp[x].size();i++){ pair<ll,ll> q=mp[x][i]; if(vis[q.first]) continue; qe=0; dis[x]=q.second; get_dis(q.first,x,q.second,2); for(int j=0;j<qe;j++){ pair<ll,ll> w=e[j]; if(flag[w.second].first<w.first){ flag[w.second].first=w.first; flag[w.second].second=1; } else if(flag[w.second].first==w.first){ flag[w.second].second++; } } } for(int i=0;i<qe2;i++){ pair<ll,ll> zz=e2[i]; flag[zz.second]=make_pair(0,0); } for(int i=0;i<mp[x].size();i++){ pair<ll,ll> q=mp[x][i]; if(vis[q.first]) continue; //if(da>0) break; sum=siz[q.first]; rt=0; maxsize[rt]=mod; find(q.first,x); divide(rt); } // vis[x]=0; } void init(){ ans1=0;ans2=0; for(int i=0;i<=n;i++) mp[i].clear(); for(int i=0;i<=n;i++) xx[i].clear(); for(int i=0;i<=n;i++) vis[i]=0; for(int i=0;i<=n;i++) xd[i]=mod; for(int i=0;i<=n;i++){ flag[i]=make_pair(0,0); } } void Dijkstra() { xd[1] = 0; priority_queue<pair<ll,ll> > Q; //priority_queue<pii,vector<pii>,greater<pii> > Q; Q.push({xd[1],1}); while(!Q.empty()) { ll now = Q.top().second; Q.pop(); if(vis[now]) continue; vis[now] = 1; for(int j = 0; j < xx[now].size(); j++) { ll v = xx[now][j].first; if(xd[v] > xd[now]+xx[now][j].second) { xd[v] = xd[now]+xx[now][j].second; Q.push({-xd[v],v}); } } } } void dfsx(ll x){ vis[x]=1; for(int i=0;i<xx[x].size();i++){ pair<ll,ll> qq=xx[x][i]; if(vis[qq.first]||xd[qq.first]!=xd[x]+qq.second) continue; mp[x].push_back(make_pair(qq.first,qq.second)); mp[qq.first].push_back(make_pair(x,qq.second)); dfsx(qq.first); } } int main(){ while(scanf("%lld%lld%lld",&n,&m,&k)!=EOF) { //if(n==0) break; ll a,b,c; init(); for(int i=1;i<=m;i++){ scanf("%lld%lld%lld",&a,&b,&c); xx[a].push_back(make_pair(b,c)); xx[b].push_back(make_pair(a,c)); } Dijkstra(); for(int i=0;i<=n;i++) vis[i]=0; dfsx(1); for(int i=0;i<=n;i++) vis[i]=0; sum=n;//当前节点数 rt=0; maxsize[0]=mod;//置初值 find(1,0); divide(rt); printf("%lld %lld\n",ans1,ans2); } }




