题目：http://codeforces.com/problemset/problem/429/B

第一个人初始位置在（1，1），他必须走到(n,m)只能往下或者往右

第二个人初始位置在（n，1），他必须走到(1,m)只能往上或者往右

每个点都有个权值，要求两个人中间相遇一次且只有一次，相遇的那个点的权值不算，两个人的速度可以不一样，然后求出最大值是多少

思路：他的要求是相遇一次且只有一次，那么画几个图其实就只有两个情况了（这图是借了一位大佬的，【小声bb】）

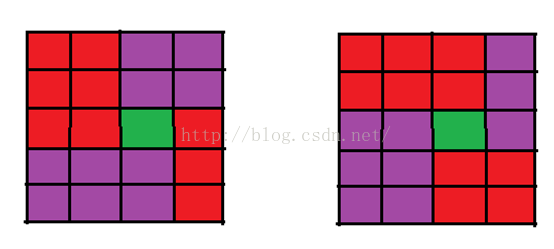
既然知道了这个图分为了这四个区域，当前格子的其他四个方向的各自都是那个人的必经过点，那么我就求出到那四个方向的最优值是多少，分别用四个dp存储

 

 

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<string>
#define maxn 1005
#define mod 1000000007
using namespace std;
typedef long long ll;
ll dp1[maxn][maxn];
ll dp2[maxn][maxn];
ll dp3[maxn][maxn];
ll dp4[maxn][maxn];
ll a[maxn][maxn];
ll n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            dp1[i][j]=max(dp1[i-1][j]+a[i][j],dp1[i][j-1]+a[i][j]);//左上角开始当起点
        }
    } 
    for(int i=1;i<=n;i++){
        for(int j=m;j>=1;j--){
            dp2[i][j]=max(dp2[i-1][j]+a[i][j],dp2[i][j+1]+a[i][j]);//右上角开始当起点
        }
    }
    for(int i=n;i>=1;i--){
        for(int j=1;j<=m;j++){
            dp3[i][j]=max(dp3[i+1][j]+a[i][j],dp3[i][j-1]+a[i][j]);//左下角开始当起点
        }
    }
    for(int i=n;i>=1;i--){
        for(int j=m;j>=1;j--){
            dp4[i][j]=max(dp4[i+1][j]+a[i][j],dp4[i][j+1]+a[i][j]);//右下角开始当起点
        }
    }
    ll mx=0;
    for(int i=2;i<n;i++){
        for(int j=2;j<m;j++){
            mx=max(mx,max(dp1[i][j-1]+dp2[i-1][j]+dp3[i+1][j]+dp4[i][j+1],dp1[i-1][j]+dp2[i][j+1]+dp3[i][j-1]+dp4[i+1][j]));//两种状态取最优
        } 
    } 
    cout<<mx;
}