【排序算法】选择排序

选择排序算法原理

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。 -- 来自百度百科

下面结合图例的方式讲解选择排序算法的原理：

第一轮排序

1.从待排序数组中选取最大数，将最大元素索引保存在maxIndex变量中( maxIndex = 0  )

2.将最大元素交换到数组末尾，swap(&arr[maxIndex], &arr[j - 1])）

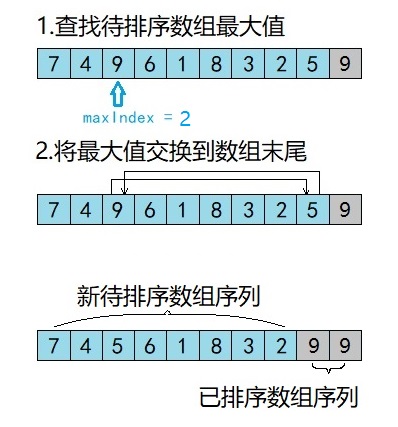
 第二轮排序

1.从待排序数组中选取最大数，将最大元素索引保存在maxIndex变量中( maxIndex = 2  )

2.将最大元素交换到数组末尾，swap(&arr[maxIndex], &arr[j - 1])）

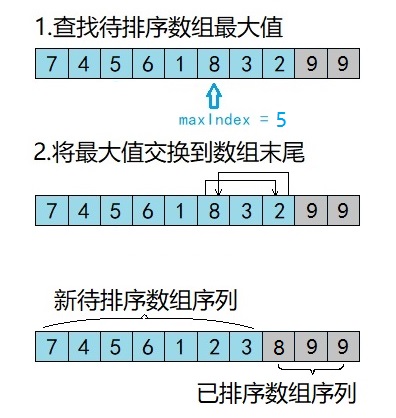
 第三轮排序

1.从待排序数组中选取最大数，将最大元素索引保存在maxIndex变量中( maxIndex = 5  )

2.将最大元素交换到数组末尾，swap(&arr[maxIndex], &arr[j - 1])）

 

 反复执行选择排序算法步骤1、2，最后得到升序序列如下

      

PS：从第1-2轮选择排序算法执行可以看出，起始数组元素序列A_[0] = A_[2] = 9，A_[0] 顺序在A_[2] 前，排序后， A_[0] 顺序在A_[2] 后，由此可见直接选择排序不是稳定排序。(深入思考：是否可以将选择排序变为稳定排序？答案：可以。只要在寻找最大值的时候， 如果元素 >= arr[maxIndex]，则保存最大元素索引，选择排序即可变为稳定排序)

排序前	A[0]	A[1]	A[2]	A[3]	A[4]	A[5]	A[6]	A[7]	A[8]	A[9]
	9	4	9	6	1	8	3	2	5	7
排序后	A[4]	A[7]	A[6]	A[1]	A[8]	A[3]	A[9]	A[5]	A[2]	A[0]
	1	2	3	4	5	6	7	8	9	9

 

选择排序算法稳定性及时间复杂度

选择排序算法稳定性：

快速排序、选择排序、希尔排序、堆排序是不稳定的排序算法，

冒泡排序、插入排序、归并排序和基数排序是稳定的排序算法。

选择排序时间复杂度：

平均情况：O(n²)、最坏情况：O(n²)、最好情况：O(n²)

选择排序算法C语言代码

#include <stdio.h>

//交换两个元素的值
void swap(int* a, int* b)
{
    int temp;
    temp = *a;
    *a = *b;
    *b = temp;
}

void selectionSort(int arr[], int length)
{
    int i, j, maxIndex;
    for(i = length; i > 0; i--)
    {
        //假设待排序的序列的最大元素为arr[0];
        maxIndex = 0;
        for(j = 1; j < i; j++)
        {
            if(arr[j] > arr[maxIndex])
                maxIndex = j;
        }
        //第二个for循环结束，找到待排序序列的最大元素的索引
        //把最大元素交换到待排序列末尾。
        swap(&arr[maxIndex], &arr[j - 1]);
    }
}

//此函数用于打印数组，和排序算法无关。
void showArray(int arr[], int length)
{
    int i;
    for(i = 0; i < length; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

int main()
{
    int arr[10] = {9,4,9,6,1,8,3,2,5,7};
    int length = sizeof(arr)/sizeof(int);
    printf("排序前:\n");
    showArray(arr, length);

    selectionSort(arr, length);

    printf("排序后:\n");
    showArray(arr, length);
    return 0;
}