【bzoj4950】【 [Wf2017]Mission Improbable】贪心+二分图匹配

（上不了p站我要死了，侵权度娘背锅）

Description
那是春日里一个天气晴朗的好日子,你准备去见见你的老朋友Patrick,也是你之前的犯罪同伙。Patrick在编程竞赛
上豪赌输掉了一大笔钱,所以他需要再干一票。为此他需要你的帮助,虽然你已经金盆洗手了。你刚开始很不情愿,
因为你一点也不想再回到那条老路上了,但是你觉得听一下他的计划也无伤大雅。在附近的一个仓库里有一批货物,
包含一些贵重的消费性部件,Patrick企图从中尽可能多地偷些东西出来。这意味着要找一条进去的路,弄晕安保人
员,穿过各种各样的激光射线,你懂的,都是常见的抢劫技术。然而,仓库的核心装备了一套Patrick搞不定的安保系
统。这也是他需要你帮助他的地方。这批货物被放置在一些巨大的立方体箱里,每个箱子的尺寸都是相同的。这些
箱子堆放成许多整齐的堆,每个箱子可以表示成一个三维的网格。安保系统每个小时会用三台相机对这堆货物进行
一次拍照,相机分别为:前置相机(front camera),侧置相机(side camera)和顶置相机(top camera)。前置相机的照
片显示了每一行最高的那堆箱子的高度,侧置相机显示了每一列最高的那堆箱子的高度,顶置相机显示了每个位置是
否存在一堆箱子。如果安保系统发现任何一张照片出现了变化,它会立即拉响警报。一旦 Patrick 进去了,他会确
定每堆箱子的高度并且发给你。图1显示了一种网格可能的放置,以及每台相机会得到的视图。

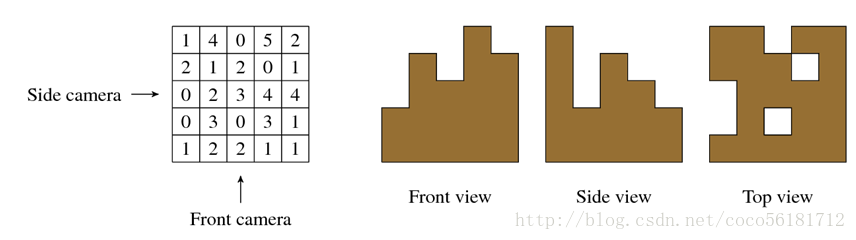
图 1. 网格的高度值与对应的相机视图。

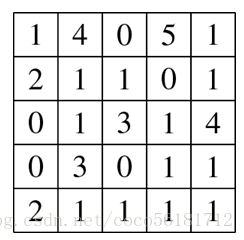
图 2. 洗劫后网格可能的高度值。
Patrick想尽可能多偷走一些箱子。由于他不能弄坏安保系统,他准备重新安排剩余每堆箱子的放置,使得下一次相
机取像时会得到相同的照片,从而骗过安保系统。在上面的例子中,他可以偷走九个箱子。图2显示了一种可能的剩
余箱子的安置方案能使得安保系统认为与原安置情况相同。Patrick想请你帮他确定在保证能骗过安保系统的情况
下他最多能偷走多少个箱子。你会帮他干完这最后一票么?
Input
第一行包含两个整数r(1≤r≤100)和c(1≤n≤100),分别表示网格的行数与列数。
接下来r行,每行包含c个整数,表示对应行上每堆立方体箱的高度(箱子的数量)。
所有的高度在0到10^9之间 (含边界) 。
Output
输出在不被发现的情况下最多能偷走多少箱子。
Sample Input
样例1
5 5
1 4 0 5 2
2 1 2 0 1
0 2 3 4 4
0 3 0 3 1
1 2 2 1 1
样例2
2 3
50 20 3
20 10 3
Sample Output
样例1
9
样例2
30

从题目中我们可以获得思路：先全部拿走，再放回去，要求放回去的值最小。（这是贪心）

那么拿走了怎么放回去呢？首先，要保证每行每列的最大高度不变，所以在拿走了之后要还回去。其次，如果把每行每列的最大值都还回去，肯定不优，因为可能某一行某一列的最大值相等，只用将这个最大值摆在交点位置就可以了。那么就将多放回去的再拿走。

但是有一个问题，如果多列的最大值和多行的最大值相等，我们难以确定让哪一个交点作为该行和该列的最大值。每一行最多有一列让我们重新拿回去，其他的最值要作为其他列的最值。
现在问题就转为了如何取走最多的物品，使得这些物品的行列不同。就是一个二分图的最大匹配了。

在“还”的时候忘记了如果这一行（列）的最高高度为0，就不用还回去。wa了我好久。。。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;

template <typename T>inline void read(T &res){
    T k=1,x=0;char ch=0;
    while(ch<'0'||ch>'9'){if(ch=='-')k=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
    res=x*k;
}

const int N=100+5;

int n,m;
ll h[N][N],rr[N],cc[N];
int bl[N];
bool vis[N];
int head[N],end[N*N],nxt[N*N],hh=0;
ll ans=0;

void adde(int a,int b){
    hh++;
    end[hh]=b;
    nxt[hh]=head[a];
    head[a]=hh;
}
bool find(int u){
    for(int i=head[u];i;i=nxt[i]){
        int v=end[i];
        if(vis[v]) continue;
        vis[v]=1;
        if(bl[v]==0||find(bl[v])){
            bl[v]=u;
            return true;
        }
    }
    return false;
}
int main(){
    read(n),read(m);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            read(h[i][j]);
            rr[i]=max(rr[i],h[i][j]);
            cc[j]=max(cc[j],h[i][j]);
            if(h[i][j]) ans+=h[i][j]-1;
        }
    }
    for(int i=1;i<=n;i++) if(rr[i]) ans-=rr[i]-1;
    for(int j=1;j<=m;j++) if(cc[j]) ans-=cc[j]-1;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            if(rr[i]==cc[j]&&h[i][j]) adde(i,j);
    for(int i=1;i<=n;i++){
        memset(vis,0,sizeof(vis));
        if(find(i)) ans+=rr[i]-1;
    }
    cout<<ans<<endl;
    return 0;
}