插值法
预备知识
我们希望通过插值去用易于计算的函数\(p(x)\)来近似一个复杂的函数\(f(x)\)，使得
\[f(x) \approx p(x)
\]
这里的“近似”是指，\(f(x)\)和\(p(x)\)在\(x\)的某些点上的值相等，如\(x_0, x_1, \cdots, x_n\)，这些点称为插值点。我们希望\(p(x)\)在这些点上的值与\(f(x)\)的值相等，即
\[f(x_i) = p(x_i), \quad i = 0, 1, \cdots, n
\]
其中，\(x_i\)称为插值节点，\(p(x_i)=f(x_i)\)称为插值条件。
什么是差商
\(f(x)\)在\(x_i\)处的零阶差商为
\[f[x_i] = f(x_i)
\]
\(f(x)\)在\(x_i\)处的一阶差商为
\[f[x_i, x_{i+1}] = \frac{f(x_{i+1}) - f(x_i)}{x_{i+1} - x_i}
\]
\(f(x)\)在\(x_i\)处的二阶差商为
\[f[x_i, x_{i+1}, x_{i+2}] = \frac{f[x_i, x_{i+1}] - f[x_{i+1}, x_{i+2}]}{x_{i+2} - x_i}
\]
| \(x_i\) |
\(f[x_i]\) |
\(f[x_i, x_{i+1}]\) |
\(f[x_i, x_{i+1}, x_{i+2}]\) |
\(f[x_i, x_{i+1}, x_{i+2}, x_{i+3}]\) |
| \(x_0\) |
\(f(x_0)\) |
|
|
|
| \(x_1\) |
\(f(x_1)\) |
\(f[x_0, x_1]\) |
|
|
| \(x_2\) |
\(f(x_2)\) |
\(f[x_1, x_2]\) |
\(f[x_0, x_1, x_2]\) |
|
| \(x_3\) |
\(f(x_3)\) |
\(f[x_2, x_3]\) |
\(f[x_1, x_2, x_3]\) |
\(f[x_0, x_1, x_2, x_3]\) |
注：差商有个特性是和排列次序无关，例如\(f[x_i, x_{i+1}] = f[x_{i+1}, x_i]\)，下面展开一下；
\[\begin{aligned}
f[x_i, x_{i+1}] &= \frac{f(x_{i+1}) - f(x_i)}{x_{i+1} - x_i} \\
&= \frac{f(x_i)}{x_i - x_{i+1}} + \frac{f(x_{i+1})}{x_{i+1} - x_i} \\
\end{aligned}
\]
我们同样有\(f[x_i, x_{i+1}, x_{i+2}] = f[x_{i+2}, x_{i+1}, x_i]\)，下面展开一下；
\[\begin{aligned}
f[x_i, x_{i+1}, x_{i+2}] &= \frac{f[x_i, x_{i+1}] - f[x_{i+1}, x_{i+2}]}{x_{i} - x_{i+2}} \\
&= \frac{\frac{f(x_{i+1}) - f(x_i)}{x_{i+1} - x_i} - \frac{f(x_{i+2}) - f(x_{i+1})}{x_{i+2} - x_{i+1}}}{x_{i} - x_{i+2}} \\
&= \frac{f(x_{i})}{(x_{i} - x_{i+1})(x_{i} - x_{i+2})} + \frac{f(x_{i+1})}{(x_{i+1} - x_{i})(x_{i+1} - x_{i+2})} + \frac{f(x_{i+2})}{(x_{i+2} - x_{i})(x_{i+2} - x_{i+1})} \\
\end{aligned}
\]
从这个形式就可以看出来没有差商的排列次序是没有意义的。
不等距节点下的牛顿基本差商公式
由一阶差商的定义，我们可以得到
\[\begin{aligned}
f[x_0,x] &= \frac{f(x) - f(x_0)}{x - x_0}\\
f[x_1,x_0,x] &= \frac{f[x_1,x_0] - f[x_0,x]}{x_1 - x}\\
f[x_2,x_1,x_0,x] &= \frac{f[x_2,x_1,x_0] - f[x_1,x_0,x]}{x_2 - x}\\
f[x_3,x_2,x_1,x_0,x] &= \frac{f[x_3,x_2,x_1,x_0] - f[x_2,x_1,x_0,x]}{x_3 - x}\\
\vdots\\
f[x_n,x_{n-1},\cdots,x_0,x] &= \frac{f[x_n,x_{n-1},\cdots,x_0] - f[x_{n-1},\cdots,x_0,x]}{x_n - x}\\
\end{aligned}
\]
这个式子可以写成(将上面依次展开，记住我们的目的我们希望表达出f(x))
\[\begin{aligned}
f(x) &= f(x_0) + f[x_0,x](x - x_0)\\
(代入f[x_0,x] &= f[x_1,x_0] + f[x_1,x_0,x](x - x_1))\\
&= f(x_0) + f[x_1,x_0](x - x_0) + f[x_1,x_0,x](x - x_1)(x - x_0)\\
(代入f[x_1,x_0,x] &= f[x_2,x_1,x_0] + f[x_2,x_1,x_0,x](x - x_2))\\
&= f(x_0) + f[x_1,x_0](x - x_0) + f[x_2,x_1,x_0](x - x_1)(x - x_0) + f[x_2,x_1,x_0,x](x - x_2)(x - x_1)(x - x_0)\\
(代入f[x_2,x_1,x_0,x] &= f[x_3,x_2,x_1,x_0] + f[x_3,x_2,x_1,x_0,x](x - x_3))\\
\vdots\\
&= f(x_0) + f[x_1,x_0](x - x_0) + f[x_2,x_1,x_0](x - x_1)(x - x_0) + \cdots + f[x_n,x_{n-1},\cdots,x_0,x](x - x_n)(x - x_{n-1})\cdots(x - x_0)\\
&= \sum_{i=0}^n f[x_i,x_{i-1},\cdots,x_0]\prod_{j=0}^{i-1}(x - x_j) + f[x_n,x_{n-1},\cdots,x_0,x]\prod_{j=0}^n(x - x_j)\\
\end{aligned}
\]
在上式中，我们令\(P_n(x) = f[x_n,x_{n-1},\cdots,x_0]\prod_{j=0}^{i-1}(x - x_j)\),令\(R_n(x) = f[x_n,x_{n-1},\cdots,x_0,x]\prod_{j=0}^n(x - x_j)\)，那么我们有
\[\begin{aligned}
f(x) &= P_n(x) + R_n(x)\\
\end{aligned}
\]
其中\(P_n(x)\)称为牛顿基本差商公式，\(R_n(x)\)称为牛顿基本差商公式的余式。
由上面公式我们容易看出，当\(x\)取\(x_0,x_1,\cdots,x_n\)时，\(R_n(x)\)即为0，\(P_n(x)\)即为\(f(x)\)。
简单例子
已知\(x=1,4,9\)的平方根值，试求\(\sqrt{7}\)的值。
解：由上面的公式我们有差商表如下(差商可以在每一列居中)
| \(x_i\) |
\(f(x_i)\) |
\(f[x_i,x_{i+1}]\) |
\(f[x_i,x_{i+1},x_{i+2}]\) |
| 1 |
1 |
|
|
| 4 |
2 |
0.33333 |
|
| 9 |
3 |
0.2 |
-0.01667 |
则差商公式为
\[\begin{aligned}
P_2(x) &= f[1] + f[1,4](x - 1) + f[1,4,9](x - 1)(x - 4) \\
&= 1 + 0.33333(x - 1) - 0.01667(x - 1)(x - 4) \\
\end{aligned}
\]
代入\(x=7\)，则有\(P_2(7) = 2.69992\) ，即\(\sqrt{7} = 2.69992\)。
f = lambda x : 1 + 0.33333*(x - 1) - 0.01667*(x - 1)*(x - 4)
f(7)
2.6999199999999997
余式估计
由拉格朗日中值定理容易证明，在\(x_0,x_1,\cdots,x_n\)上的存在\(\xi\)使得\(f[x_0,x_1,\cdots,x_n] = \frac{f^{(n)}(\xi)}{n!}\)，则有\(f[x_n,x_{n-1},\cdots,x_0,x] = \frac{f^{(n + 1)}(\xi)}{(n + 1)!}\)
\[R_n(x) = f[x_n,x_{n-1},\cdots,x_0,x]\prod_{j=0}^n(x - x_j)
= \frac{f^{(n + 1)}(\xi)}{(n + 1)!}\prod_{j=0}^n(x - x_j)
\]
对于上面的例子，我们有
\[\begin{aligned}
f(x) = \sqrt{x} \\
f^{(1)}(x) = \frac{1}{2\sqrt{x}} \\
f^{(2)}(x) = -\frac{1}{4x^{3/2}} \\
f^{(3)}(x) = \frac{3}{8x^{5/2}} \\
\end{aligned}
\]
可知\(f^{(3)}(x)\)单调递减，则有\(f^{(3)}(x) \leq f^{(3)}(1) = \frac{3}{8}\)，则有
\[\begin{aligned}
|R_2(x)| &\leq \frac{3}{8}|\prod_{j=0}^2(x - x_j)| \\
&= \frac{3}{8}|(x - 1)(x - 4)(x - 9)| \\
\end{aligned}
\]
则有\(|R_2(7)| \leq 13.5\)，这显然不符合我们余式估计的要求，我们需要更多的值或者方法来估计余式。
3/8 * (7-1)*(7-4)*(7-9)
-13.5
事后估计误差法
在上面中我们选取的牛顿差商公式为\(P_n(x)\)，插值节点为\(x_0,x_1,\cdots,x_n\)，
\[\begin{aligned}
P_n(x) &= \sum_{i=0}^n f[x_i,x_{i+1},\cdots,x_n]\prod_{j=0}^{i-1}(x - x_j) \\
R_n(x) &= f[x_n,x_{n-1},\cdots,x_0,x]\prod_{j=0}^n(x - x_j) \\
\end{aligned}
\]
若我们选取的插值节点为\(x_1,\cdots,x_{n + 1}\)，则有
\[\begin{aligned}
P_n^{(1)}(x) &= \sum_{i=1}^{n + 1} f[x_i,x_{i+1},\cdots,x_{n + 1}]\prod_{j=1}^{i-1}(x - x_j) \\
R_n^{(1)}(x) &= f[x_{n+1},x_n,\cdots,x_1,x]\prod_{j=1}^{n+1}(x - x_j) \\
\end{aligned}
\]
则两个余式的比值为
\[\begin{aligned}
\frac{R_n(x)}{R_n^{(1)}(x)} &= \frac{f[x_n,x_{n-1},\cdots,x_0,x]\prod_{j=0}^n(x - x_j)}{f[x_{n+1},x_n,\cdots,x_1,x]\prod_{j=1}^{n+1}(x - x_j)}
&= \frac{f[x_n,x_{n-1},\cdots,x_0,x]}{f[x_{n+1},x_n,\cdots,x_1,x]} * \frac{\prod_{j=0}^n(x - x_j)}{\prod_{j=1}^{n+1}(x - x_j)} \\
&= \frac{f[x_n,x_{n-1},\cdots,x_0,x]}{f[x_{n+1},x_n,\cdots,x_1,x]} * \frac{x - x_0}{x - x_{n + 1}} \\
\end{aligned}
\]
因为\(f[x_n,x_{n-1},\cdots,x_0,x]\)和\(f[x_{n+1},x_n,\cdots,x_1,x]\)都是关于\(x\)的高阶差商，我们这里认为它们的值是几乎相等的，再者我们有\(R_n^{(1)}(x) = f(x) - P_n^{(1)}(x) = P_n(x) + R_n(x)- P_n^{(1)}(x)\)，则有
\[\begin{aligned}
\frac{R_n(x)}{R_n^{(1)}(x)} = \frac{R_n(x)}{R_n(x) + P_n(x) - P_n^{(1)}(x)} &= \frac{x - x_0}{x - x_{n + 1}}\\
\Rightarrow (x - x_0)R_n(x) + (x - x_0)(P_n(x) - P_n^{(1)}(x)) &= (x - x_{n + 1})R_n(x)\\
\Rightarrow (x_0 - x_{n + 1})R_n(x) &= (x - x_0)(P_n(x) - P_n^{(1)}(x))\\
\Rightarrow R_n(x) &= \frac{x - x_0}{x_0 - x_{n + 1}}(P_n(x) - P_n^{(1)}(x)) \\
\end{aligned}
\]
简单例子2
已知\(x_0 = 4, x_1 = 9, x_2 = 6.25, x_4 = 4.84\)，求\(\sqrt{7}\)的值。
解：由于\(x_0 = 4, x_1 = 9, x_2 = 6.25, x_4 = 4.84\)，所以我们可以用牛顿插值公式求出\(P_2(7)\)，
差商表如下：
| \(x\) |
\(f(x)\) |
\(f[x_i,x_{i+1}]\) |
\(f[x_i,x_{i+1},x_{i+2}]\) |
| 4 |
2 |
|
|
| 9 |
3 |
0.2 |
|
| 6.25 |
2.5 |
0.18182 |
-0.00808 |
| 4.84 |
2.2 |
0.21277 |
-0.00744 |
\[\begin{aligned}
P_2(7) &= 2 + 0.2(7 - 4) - 0.00808(7 - 4)(7 - 9) = 2.64848 \\
\end{aligned}
\]
余式估计: 由\(f(x) = \sqrt{x}\)，我们有\(f^{(3)}(x) = \frac{3}{8}x^{-\frac{5}{2}}\)，在区间\([4,9]\)上，\(f^{(3)}(x)\)的最大值为\(\frac{3}{8}4^{-\frac{5}{2}} = 0.01171875\)，所以有
\[\begin{aligned}
R_2(7) &= f[4,9,6.25](7 - 4)(7 - 9)(7 - 6.25) \\
&= \frac{f^{(3)}(\xi)}{3!}(7 - 4)(7 - 9)(7 - 6.25) \\
&\leq \frac{0.01171875}{6}(7 - 4)(7 - 9)(7 - 6.25) \\
&= -0.0087890625 \\
\end{aligned}
\]
事后估计法：
\[\begin{aligned}
P_2^{(1)}(7) &= 3 + 0.18182(7 - 9) + 0.00744(7 - 9)(7 - 6.25) = 2.64752 \\
R_2(7) &= \frac{7 - 4}{4 - 4.84} * (P_2(7) - P_2^{(1)}(7)) = -0.00343 \\
\end{aligned}
\]
由事后估计法得到的余式近似\(0.5*10^{-2}\)，\(P_2(7)\)的值可舍入为\(2.65\)，所以\(\sqrt{7} \approx 2.65\)。
差分
在不等距节点的基础上我们特殊化，假如\(x_0, x_1, \cdots, x_n\)是等距的，即\(x_i - x_{i - 1} = h\)，则称为等距节点，其每一个节点对应的值为\(y_0, y_1, \cdots, y_n\)，我们称为差分，记为\(y_i = f(x_i)\)，则称
\[\begin{aligned}
\Delta y_{i-1} = y_i - y_{i - 1} &= f(x_i) - f(x_{i - 1}) \text{\quad(1)} \\
\text{(1)称为一阶差分，例如}\Delta y_0 &= y_1 - y_0 \\
\Delta^2 y_{i-2} = \Delta y_{i-1} - \Delta y_{i-2} &= f(x_i) - 2f(x_{i - 1}) + f(x_{i - 2}) \text{\quad(2)} \\
\text{(2)称为二阶差分，例如}\Delta^2 y_0 &= \Delta y_1 - \Delta y_0 \\
\Delta^3 y_{i-3} = \Delta^2 y_{i-2} - \Delta^2 y_{i-3} &= f(x_i) - 3f(x_{i - 1}) + 3f(x_{i - 2}) - f(x_{i - 3}) \text{\quad(3)} \\
\text{(3)称为三阶差分，例如}\Delta^3 y_0 &= \Delta^2 y_1 - \Delta^2 y_0 \\
\end{aligned}
\]
注：其系数我们发现其实和二项式展开式很相像的，我们不妨写一下二项式展开式来对比
\[\begin{bmatrix}
(a-b)^1 = a - b &\rightarrow &\Delta y_{i-1} = f(x_i) - f(x_{i - 1}) \\
(a-b)^2 = a^2 - 2ab + b^2 &\rightarrow &\Delta^2 y_{i-2} = f(x_i) - 2f(x_{i - 1}) + f(x_{i - 2}) \\
(a-b)^3 = a^3 - 3a^2b + 3ab^2 - b^3 &\rightarrow &\Delta^3 y_{i-3} = f(x_i) - 3f(x_{i - 1}) + 3f(x_{i - 2}) - f(x_{i - 3}) \\
\end{bmatrix}
\]
则我们可以得到\(x_i = x_0 + ih\)，\(y_i = f(x_0 + ih)\)，则有（用差分表示差商）
\[\begin{aligned}
f[x_0,x_1] &= \frac{f(x_1) - f(x_0)}{x_1 - x_0} = \frac{y_1 - y_0}{h} = \frac{\Delta y_0}{h} \\
f[x_0,x_1,x_2] &= \frac{f[x_1,x_2] - f[x_0,x_1]}{x_2 - x_0} = \frac{\Delta y_1 - \Delta y_0}{2h} = \frac{\Delta^2 y_0}{2h^2} \\
f[x_0,x_1,x_2,x_3] &= \frac{f[x_1,x_2,x_3] - f[x_0,x_1,x_2]}{x_3 - x_0} = \frac{\Delta^2 y_1 - \Delta^2 y_0}{3h} = \frac{\Delta^3 y_0}{6h^3} \\
\vdots \\
f[x_0,x_1,\cdots,x_n] &= \frac{f[x_1,x_2,\cdots,x_n] - f[x_0,x_1,\cdots,x_{n-1}]}{x_n - x_0} = \frac{\Delta^{n} y_0}{n!h^n} \\
\end{aligned}
\]
牛顿基本差商公式为：
\[\begin{aligned}
f(x) &= P_n(x) + R_n(x) \\
P_n(x) &= \sum_{i=0}^n f[x_0,x_1,\cdots,x_i] \prod_{j=0}^{i-1} (x - x_j) \\
R_n(x) &= f[x_0,x_1,\cdots,x_n,x] \prod_{j=0}^{n} (x - x_j) \\
\end{aligned}
\]
用差分代替差商，我们得到牛顿前向插值公式：
\[\begin{aligned}
P_n(x) &= y_0 + \frac{\Delta y_0}{h} (x - x_0) + \frac{\Delta^2 y_0}{2h^2} (x - x_0)(x - x_1) + \frac{\Delta^3 y_0}{6h^3} (x - x_0)(x - x_1)(x - x_2) + \cdots + \frac{\Delta^{n} y_0}{n!h^n} (x - x_0)(x - x_1)\cdots(x - x_{n-1}) \\
&= y_0 + \sum_{i=1}^n \frac{\Delta^i y_0}{i!h^i} \prod_{j=0}^{i-1} (x - x_j) \\
\end{aligned}
\]
令\(t = \frac{x - x_0}{h}\)，则有
\[\begin{aligned}
P_n(x) &= y_0 + \Delta y_0 t + \frac{\Delta^2 y_0}{2} t(t - 1) + \frac{\Delta^3 y_0}{6} t(t - 1)(t - 2) + \cdots + \frac{\Delta^{n} y_0}{n!} t(t - 1)\cdots(t - n + 1) \\
&= y_0 + \sum_{i=1}^n \frac{\Delta^i y_0}{i!} t(t - 1)\cdots(t - i + 1) \\
&= y_0 + c_t^1 \Delta y_0 + c_t^2 \Delta^2 y_0 + c_t^3 \Delta^3 y_0 + \cdots + c_t^n \Delta^n y_0 \\
\end{aligned}
\]
其中\(c_t^i = \frac{t(t - 1)\cdots(t - i + 1)}{i!}\)，称为牛顿基本差商的系数。
牛顿前向插值公式的余项为
\[\begin{aligned}
R_n(x) &= f[x_0,x_1,\cdots,x_n,x] \prod_{j=0}^{n} (x - x_j) \\
&= f[x_0,x_1,\cdots,x_n,x] \prod_{j=0}^{n} (x - x_0 - jh) \\
&= \frac{f^{(n+1)}(\xi)}{(n+1)!} h^{n+1} \prod_{j=0}^{n} (t - j) \\
\end{aligned}
\]
同理由差商表最后一行可得牛顿后向插值公式：
\[\begin{aligned}
P_n(x) &= y_n + \frac{\Delta y_{n-1}}{h} (x - x_n) + \frac{\Delta^2 y_{n-2}}{2h^2} (x - x_n)(x - x_{n-1}) + \frac{\Delta^3 y_{n-3}}{6h^3} (x - x_n)(x - x_{n-1})(x - x_{n-2}) + \cdots + \frac{\Delta^{n} y_0}{n!h^n} (x - x_n)(x - x_{n-1})\cdots(x - x_{1}) \\
&= y_n + \sum_{i=1}^n \frac{\Delta^i y_{n-i}}{i!h^i} \prod_{j=0}^{i-1} (x - x_{n-j}) \\
\end{aligned}
\]
令\(t = \frac{x - x_n}{h}\)，则有
\[\begin{aligned}
P_n(x) &= y_n + \Delta y_{n-1} t + \frac{\Delta^2 y_{n-2}}{2} t(t + 1) + \frac{\Delta^3 y_{n-3}}{6} t(t + 1)(t + 2) + \cdots + \frac{\Delta^{n} y_0}{n!} t(t + 1)\cdots(t + n - 1) \\
&= y_n + \sum_{i=1}^n \frac{\Delta^i y_{n-i}}{i!} t(t + 1)\cdots(t + i - 1) \\
&= y_n + c_t^1 \Delta y_{n-1} + c_{t+1}^2 \Delta^2 y_{n-2} + c_{t+2}^3 \Delta^3 y_{n-3} + \cdots + c_{t+n-1}^n \Delta^n y_0 \\
\end{aligned}
\]
其中\(c_t^i\)与上面的相同（课件中明显写错了）。
牛顿后向插值公式的余项为
\[\begin{aligned}
R_n(x) &= f[x_0,x_1,\cdots,x_n,x] \prod_{j=0}^{n} (x - x_j) \quad\text{注意到这里是从后往前减的}x_j = x_n - jh \\
&= f[x_0,x_1,\cdots,x_n,x] \prod_{j=0}^{n} (x - x_n + jh) \\
&= \frac{f^{(n+1)}(\xi)}{(n+1)!} h^{n+1} \prod_{j=0}^{n} (t + j) \\
\end{aligned}
\]
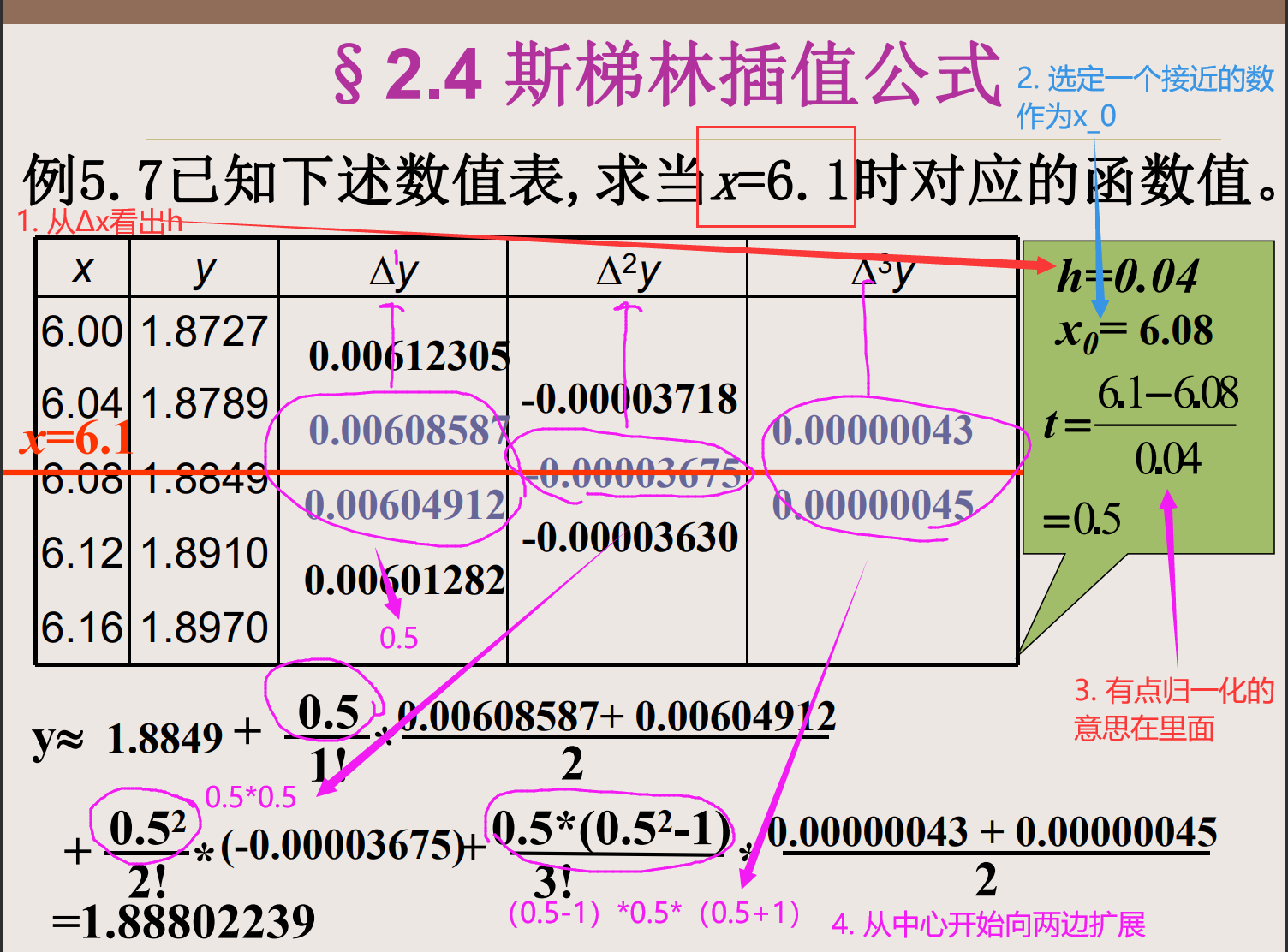
斯梯林插值公式
斯梯林插值公式是牛顿插值公式的一种推广，它的基本思想是将插值点分成两组，分别用牛顿插值公式求出两组的插值多项式，然后将两个多项式相加得到斯梯林插值公式。
这里认为只要记住下面两幅图即可，推导过程略；
不等距节点下的拉格朗日插值公式
推导
在上面知识的基础上，我们设\(x\)为\(x_0, x_1, \cdots, x_n\)这个插值区间中的任意一个点，则有
由上面证明顺序性的类似结论，我们可以得到
\[\begin{aligned}
f[x_0,x] & = \frac{f(x) - f(x_0)}{x - x_0} = \frac{f(x_0)}{x_0 - x} + \frac{f(x)}{x - x_0} \\
f[x_0,x_1,x] & = \frac{f(x_0)}{(x_0 - x_1)(x_0 - x)} + \frac{f(x_1)}{(x_1 - x_0)(x_1 - x)} + \frac{f(x)}{(x - x_0)(x - x_1)} \\
f[x_0,x_1,x_2,x] & = \frac{f(x_0)}{(x_0 - x_1)(x_0 - x_2)(x_0 - x)} + \frac{f(x_1)}{(x_1 - x_0)(x_1 - x_2)(x_1 - x)} + \frac{f(x_2)}{(x_2 - x_0)(x_2 - x_1)(x_2 - x)} + \frac{f(x)}{(x - x_0)(x - x_1)(x - x_2)} \\
f[x_0,x_1,\cdots,x_n,x] & = \sum_{i=0}^n \frac{f(x_i)}{(x_i - x)\prod_{j=0, j \neq i}^n (x_i - x_j)} + \frac{f(x)}{\prod_{j=0}^n (x - x_j)} \\
\end{aligned}
\]
我们将上式同乘以\((x - x_0)(x - x_1)\cdots(x - x_n)\)，（即\(\prod_{j=0}^n (x - x_j)\)），则有
\[\begin{aligned}
f[x_0,x_1,\cdots,x_n,x]\prod_{j=0}^n (x - x_j) & = \sum_{i=0}^n \frac{f(x_i)*\prod_{j=0}^n (x - x_j)}{(x_i - x)\prod_{j=0, j \neq i}^n (x_i - x_j)} + f(x)
\end{aligned}
\]
移项一下我们有
\[\begin{aligned}
f(x) &= -\sum_{i=0}^n \frac{f(x_i)*\prod_{j=0}^n (x - x_j)}{(x_i - x)\prod_{j=0, j \neq i}^n (x_i - x_j)} + f[x_0,x_1,\cdots,x_n,x]\prod_{j=0}^n (x - x_j) \\
&= \sum_{i=0}^n \frac{f(x_i)*\prod_{j=0, j \neq i}^n (x - x_j)}{\prod_{j=0, j \neq i}^n (x_i - x_j)} + f[x_0,x_1,\cdots,x_n,x]\prod_{j=0}^n (x - x_j) \\
\end{aligned}
\]
在上式中，我们令\(L_n(x) = \sum_{i=0}^n \frac{\prod_{j=0, j \neq i}^n (x - x_j)}{\prod_{j=0, j \neq i}^n (x_i - x_j)}f(x_i)\), \(R_n(x) = f[x_0,x_1,\cdots,x_n,x]\prod_{j=0}^n (x - x_j)\)，则有
\[\begin{aligned}
f(x) &= L_n(x) + R_n(x) \\
\end{aligned}
\]
其中的\(L_n(x)\)称为拉格朗日插值公式，\(R_n(x)\)就是其余项。
其它还有诸如下面的一些插值方法，课本上的写的也很详细，这里就不再赘述了。（主要是好多式子！！！）
- 等距节点下的拉格朗日插值公式
- 反向插值
- 埃尔米特插值
- 多元函数的插值
