重新研究一下浮点数的内部储存机制
重新研究一下浮点数的内部储存机制
写这篇文章的原因有很多,学校大一上学期开展的大学计算机没有把浮点数学懂,或者说也没想着讲明白,这篇文章写在考完C语言期末考试的第六天,希望通过利用浙大C语言
mooc建议的一个转二进制网站和联合这个好工具来重新理解浮点数的储存方式---2022.6.29
浮点数组成
\[由国际标准IEEE 754规定,任意一个二进制浮点数V都可以表示成下列形式:\\
V=(-1)^{Sign}*M*2^{Exponent}
\]
| float | Sign(符号位) | Exponent(指数位) | Mantissa(尾数位) |
|---|---|---|---|
| 32bit | 1 | 8 | 23 |
| double | Sign(符号位) | Exponent(指数位) | Mantissa(尾数位) |
|---|---|---|---|
| 64bit | 1 | 11 | 52 |
例子分析
代码
typedef union{//CHF这样我们可以访问到float里面的内存
float value;
char mem[sizeof(float)];
}MEMF;
typedef union{//CHD这样我们可以访问到double里面的内存
double value;
char mem[sizeof(double)];
}MEMD;
直接定义两个联合体,同时以value的类型存值,同时可以用mem去输出每一字节的储存情况,从而达到研究浮点数储存方式的效果;我们下面首先研究单精度浮点数float的储存方式;
void demo1() {
MEMF a;
a.value=0.5;
printf("%.2f|", a.value);
for (unsigned i = 0; i < sizeof(float); i++) {
printf("%02hhX ", a.mem[i]);
}
}
%02hhX出现很多次了,是指以一个字节的形式的十六进制输出,2位,少的补零;可以参考%02hhX- 上面程序就是从左往右输出内存空间二进制分布的字节形式,输出如下:
0.50|00 00 00 3F
分析
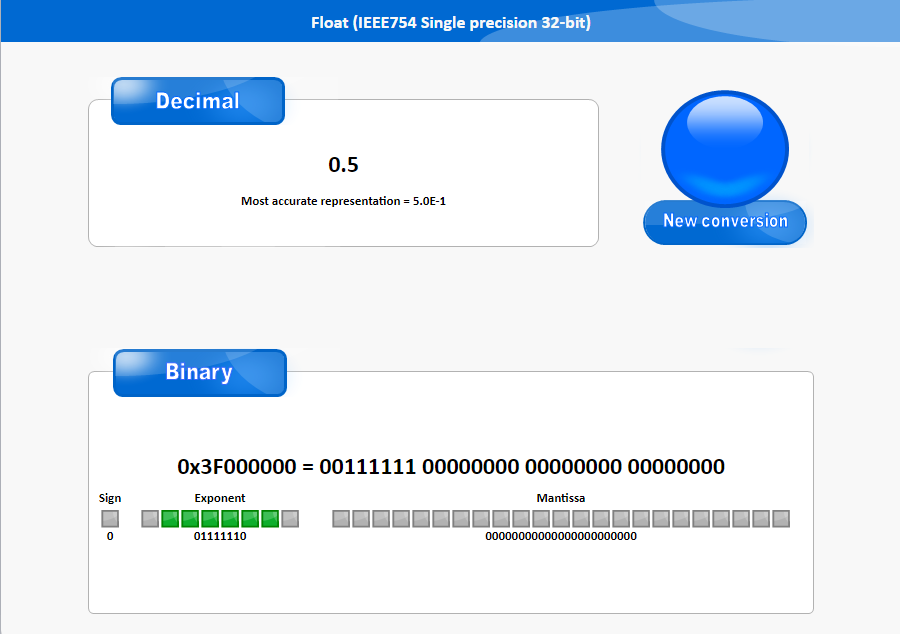
- 由机器的小端存储方式(字节序与内存序相反)我们知道实际的应该是
3F 00 00 00,在网站中验证如下图:
-
0011 1111=3F,0000 0000=00,左边为二进制,右边为十六进制 -
Sign=0说明是正数,Exponent=01111110第一个0是符号的意思,0为负数,1为正数,1111110不难发现表达的是1的意思(指数位采用的类似反码的表示方法,但最左边第一位不同),则表示成十进制Exponent=01111110=-1;那么,如果我们把最令Exponent=01111111=0,其它位不变,则表示什么呢——就是1,因为我们的尾数会把1省略掉,即M默认是1;
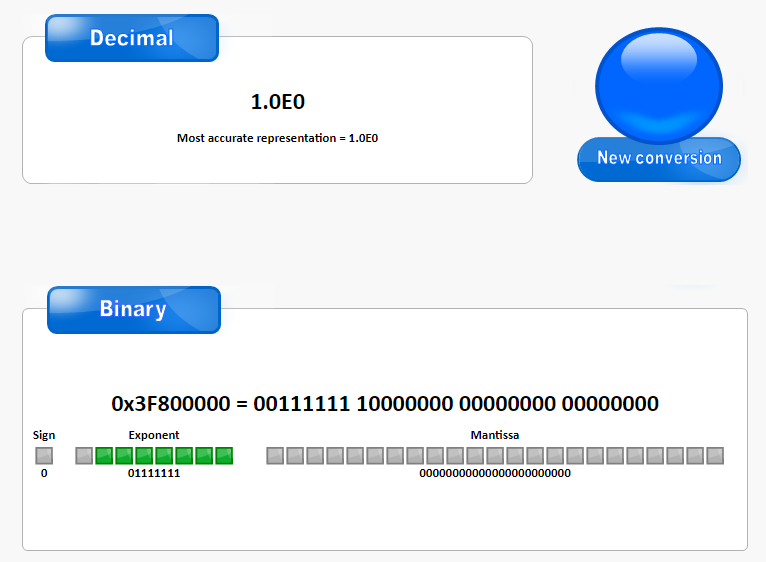
归纳(猜测着总结):
\[\begin{align}
0.5 & = (-1)^{Sign}*M*2^{Exponent}\\
& = (-1)^{0}*1*2^{-1}\\
&=
\mathop{0}_{1\;bit}^{(-1)_{\uparrow}^{0}}\;
\underbrace{01111110}_{8\;bits}^{2_{\;\uparrow}^{-1}}\;
\underbrace{0000000\;00000000\;00000000}_{23\;bits}
\end{align}
\]
演绎(尝试着解释):
\[\begin{align}
0.25 & = (-1)^{Sign}*M*2^{Exponent}\\
& = (-1)^{0}*1*2^{-2}\\
&=
\mathop{0}_{1\;bit}^{(-1)_{\uparrow}^{0}}\;
\underbrace{01111101}_{8\;bits}^{2_{\;\uparrow}^{-2}}\;
\underbrace{0000000\;00000000\;00000000}_{23\;bits}
\end{align}
\]
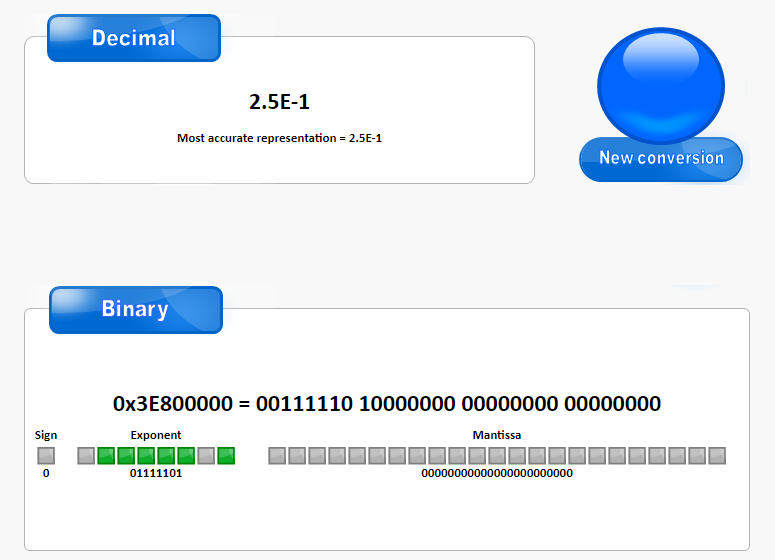
再试了几个例子,觉得应该改一下猜测
我们的Exponent好像并不是用反码的形式,发现应该是这样的;
将Exponent左边第一位取反,再对Exponent取补码即为所得结果:
\[0111\;1110\\
\Rightarrow1111\;1110\\
\Rightarrow1\;0000\;0000-1111\;1110\\
\Rightarrow0000 0010=2\\
\Rightarrow2^{1-2}=0.5
\]
\[即对于float来说\\
2^{1+Exponent-2^{8-1}}=2^{Exponent-127}
才是指数位真正的因子
\]
几行例子快速明白
\[\begin{align}
0.5 & = (-1)^{\overbrace{0}^{Sign}}\times
2^{\overbrace{0111\;1110}^{Exponent}-0111\;1111}\times
{(1\times2^0+\overbrace{0\times2^{-1}+0\times2^{-2}+\cdots}^
{\overbrace{0000000\;00000000\;00000000}^{Mantissa}})}\\
& = 1\times2^{-1}\times1\\
& = 0.5
\end{align}
\]
\[\begin{align}
-123.5 & = (-1)^{\overbrace{1}^{Sign}}\times
2^{\overbrace{1000\;0101}^{Exponent}-0111\;1111}\times
{(1\times2^0+\overbrace{1\times2^{-1}+1\times2^{-2}+\cdots}^
{\overbrace{1110111\;00000000\;00000000}^{Mantissa}})}\\ & = (-1)\times2^{0000\;0110}\times
(1\times2^0+1\times2^{-1}+1\times2^{-2}+1\times2^{-3}+0\times2^{-4}+1\times2^{-5}+1\times2^{-6}+1\times2^{-7})\\ & = (-1)\times2^{6}\times(1+2^{-1}+2^{-2}+2^{-3}+2^{-5}+2^{-6}+2^{-7})\\ & = (-1)\times(2^{6}+2^5+2^4+2^3+2^1+2^0+2^{-1})\\ & = -123.5
\end{align}
\]
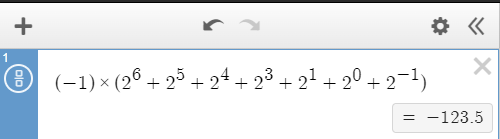
🌹desmos等很多数学计算网站都是支持latex公式直接计算的,上面这个式子的计算就是直接复制最后一行的结果;
总结
单精度浮点数的公式是
\[F=(-1)^{Sign}\times2^{Exponent-{2^7}+1}\times(1.Mantissa)_2\\
其中上面三个参数都是直接替换成二进制然后转化成十进制运算即可,其中\\
(1.Mantissa)_2=1+(0.Mantissa)_2\\
我们总是会保留个1出来所以Mantissa也被翻译成尾数部分,比如(0.1)_2=0.5
\]
其实研究完单精度我们的双精度也很容易理解现在了,就是Exponent部分变成十一位,相应的公式也应该是
\[D=(-1)^{Sign}\times2^{Exponent-2^{10}+1}\times(1.Mantissa)
\]
工具:
- 这个研究二进制的超好网站Online Binary-Decimal Converter (binaryconvert.com)
- Dev-C++
- Desmos | 图形计算器


 浙公网安备 33010602011771号
浙公网安备 33010602011771号