Weights Initialization

Weights Initialization

(话说在前头，可能这才是深度学习中最重要的地方)

What if you initialize weights to zero?

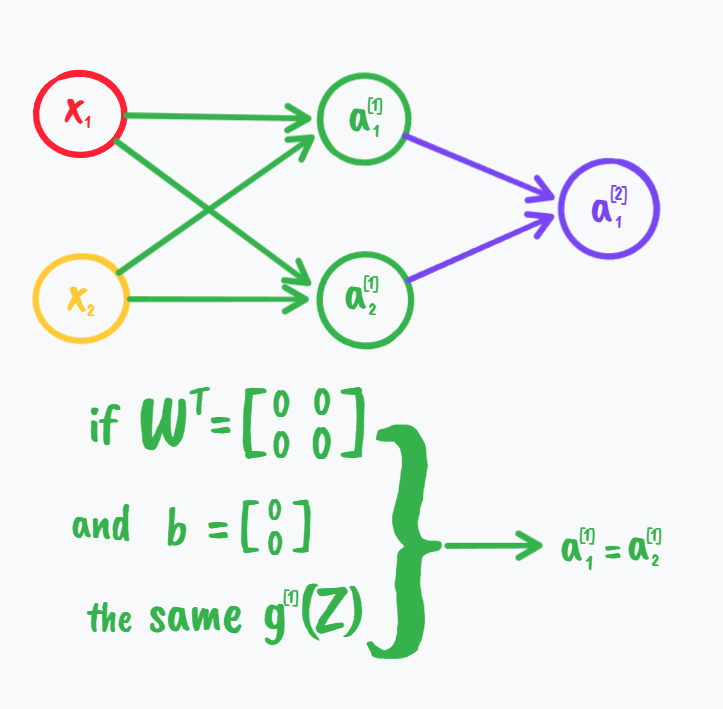
如果权重全部初始化为零，我们知道此时第一层所有的a都是对称的；这也就导致了后面我们得到的dW是每行都一样的（笔者认为此时如果b也初始化为零，那么dW甚至每一列都是一样的），迭代更新后对W本身也是如此，那么从线性代数的角度去看，W这个矩阵的秩为一，就导致了维度的丧失，我们没有完全地代表我们的特征数据，这只是一个维度而已；

所以我们提出的解决方法是：随机初始化:

$$W^{[1]}=np.random.randn((2,2))*0.01\\ (Andrew说这里是Gaussian random variable即高斯分布随机变量)\\ b^{[1]}=np.zeros((2,1))\\ W^{[2]}=np.random.randn((1,2))*0.01\\ b^{[1]}=np.zeros((2,1)$$

可能有人会对后面乘以的0.01产生疑惑：这可以回忆起我们tanh或sigmoid函数，我们知道当变量值大到一定程度时，此时的梯度下降法的迭代是相当缓慢的，如下图

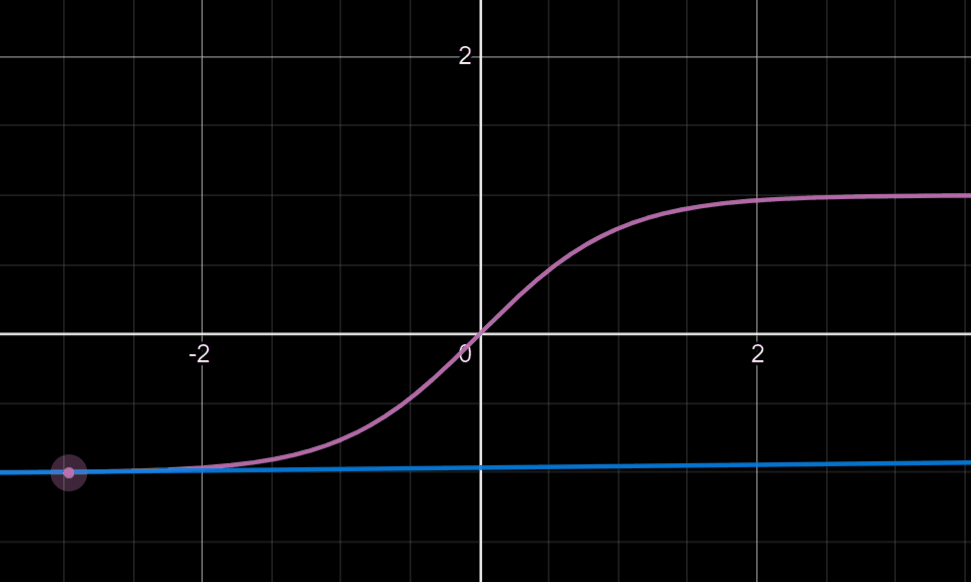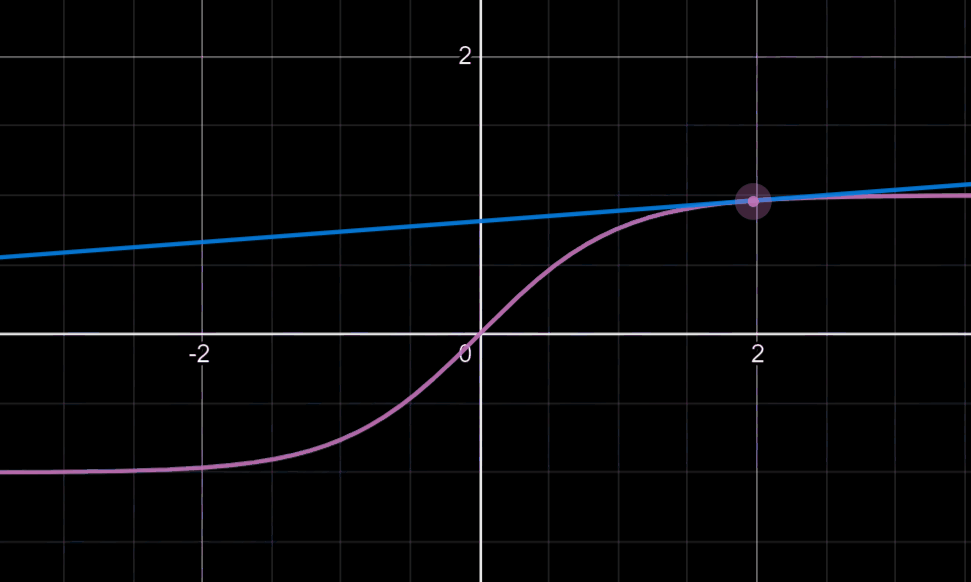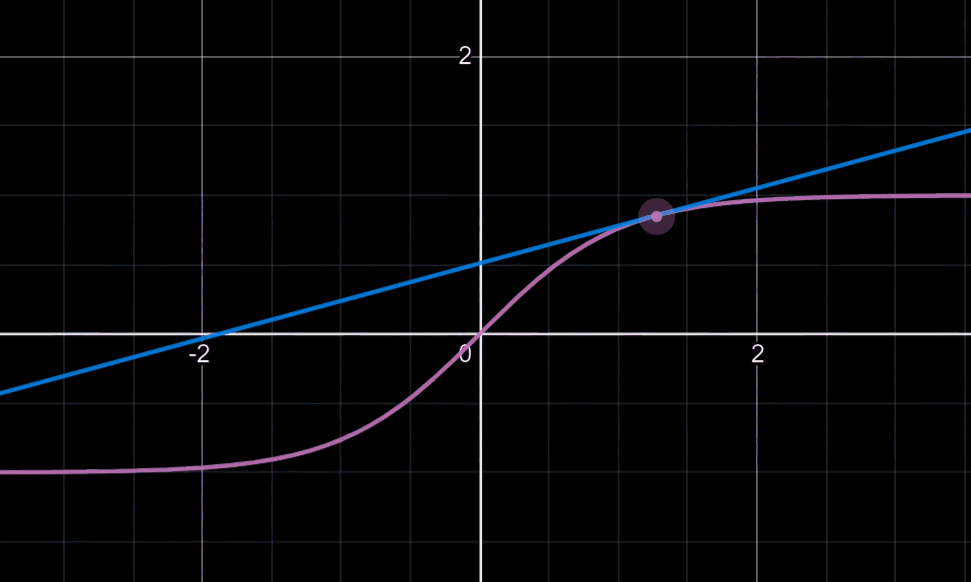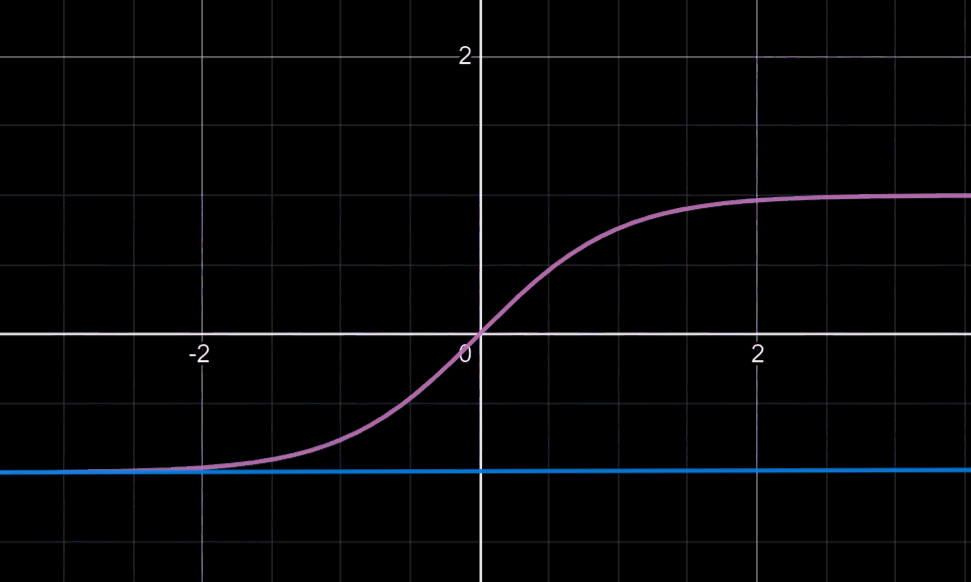
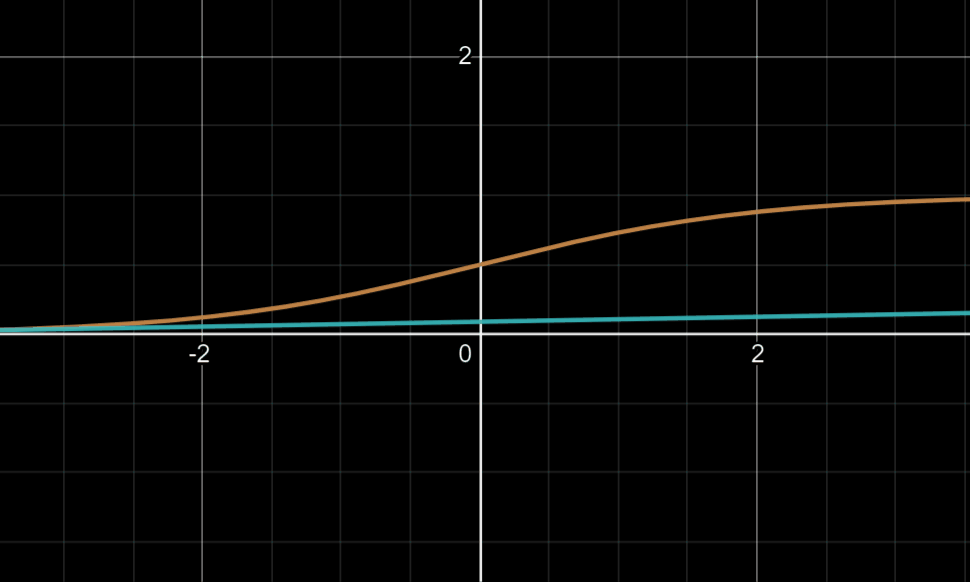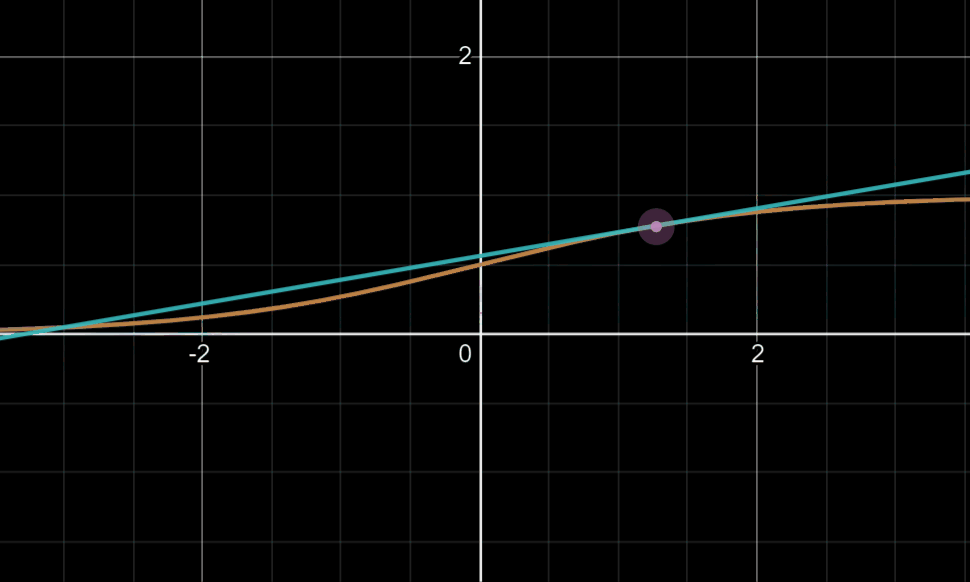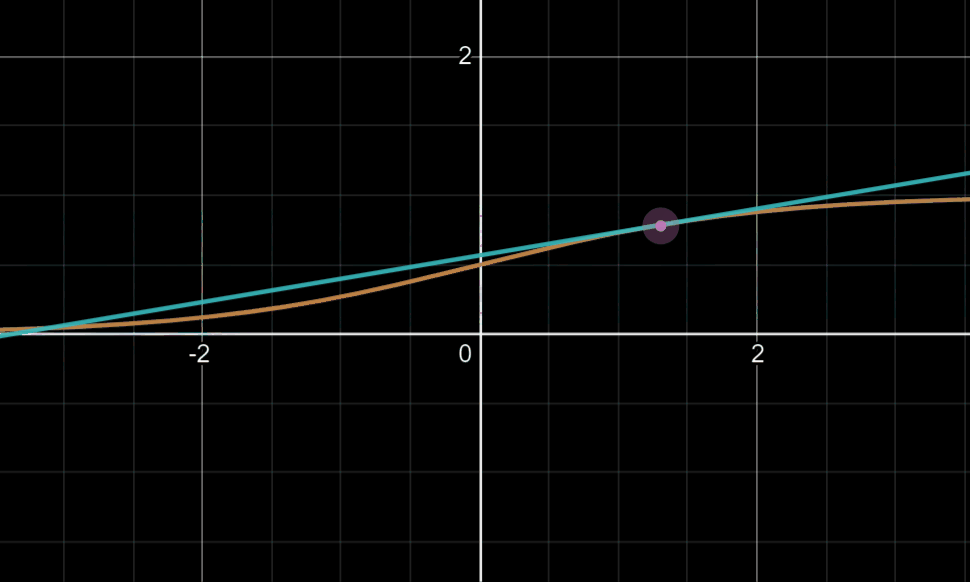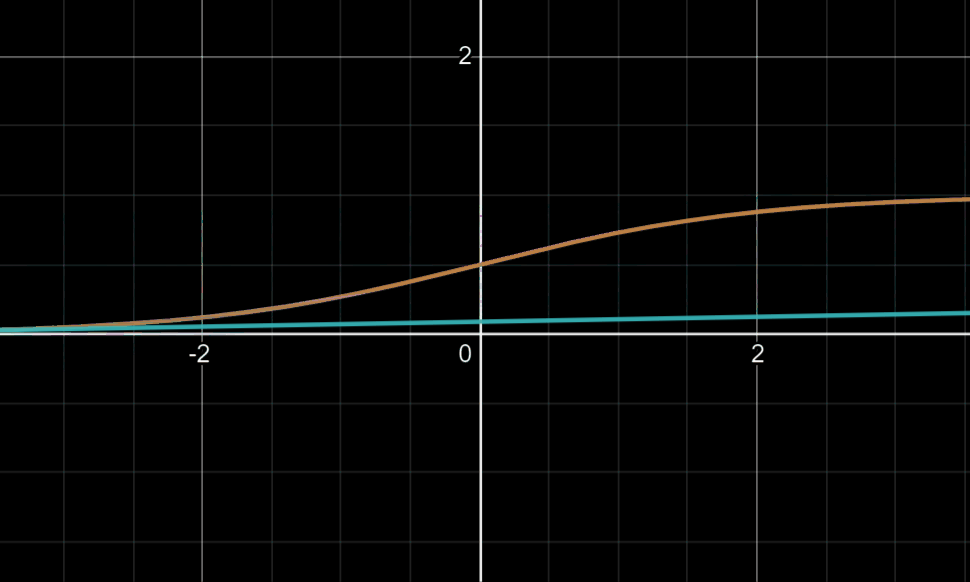
所以乘以0.01的目的往往在于使更多的变量落于梯度变化明显的地方，就是说我们希望W是一个较小的随机权重矩阵。

Andrew表示在后面的深度网络中，相比于乘以0.01，我们还会继续学习更多地参数初始化的方法。

---