Gradient descent for neural networks
还是针对之前概览中的这个网络,并且考虑它做的是binary classification;
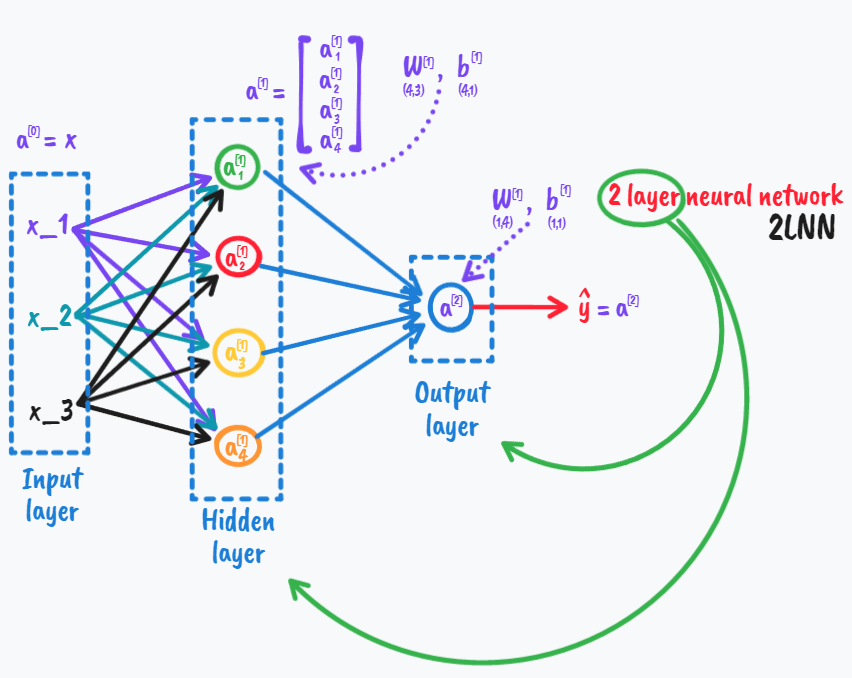
则我们现在来讨论其中的梯度下降方法,
Parameters(参数):W[1](n[1],n[0]),b[1](n[1],1),W[2](n[2],n[1]),b[2](n[2],1)nx=n[0],n[1],n[2]=1Costfunction:J(W[1],b[1],W[2],b[2])=1mn∑i=1L(^y↑a[2],y)Gradientdescent:Repeat:Computepredictions(^y(i),i=1,⋯,m)dW[1]=∂J∂W[1],db[1]=∂J∂b[1],dW[2]=∂J∂W[2],db[2]=∂J∂b[2],W[1]:=W[1]−αdW[1]b[1]:=b[1]−αdb[1]W[2]:=W[2]−αdW[2]b[2]:=b[2]−αdb[2](注意:α是学习率,[:=]也可以写成[=],只不过为了更好表示迭代)
那么问题现在显而易见:我们如何去求偏导数呢?
Formalpropagation:Z[1]=W[1]X+b[1]A[1]=g[1](Z[1])Z[2]=W[2]A[1]+b[2]A[2]=g[2](Z[2])=σ(Z[2])
Backpropagation:dZ[2]=A[2]−Y其中Y=[y[1],y[2],⋯,y[m]]dW[2]=1mdZ[2]A[1]Tdb[2]=1mnp.sum(dZ[1],axis=1,tomaintaindb[2]isn′t(n[2],)but(n[2],1)keepdims=True)dZ[1]=W[2]TdZ[2](n[1],m)∗g[1]′(Z[1])(n[1],m)∗是对应元素相乘dW[1]=1mdZ[1]XTdb[1]=1mnp.sum(dZ[1],axis=1,tomaintaindb[1]isn′t(n[1],)but(n[1],1)keepdims=True)
下面来直观理解一下这个反向传播过程(通过逻辑斯蒂回归);
x↘ω→b↗(1)(2)(3)z=ωTx+b→a=σ(z)→L(a,y)L(a,y)=−yloga−(1−y)log(1−a)
(注意:我们下面的dz,da等等d开头的记法都是指导数的意思可以理解为最终那个损失函数对d后面的变量取导数)
da=∂L(a,y)∂a=−ya+1−y1−a
dz=da⋅g′(z)(这里的g(z)=σ(z))原因很简单:∂L(a,y)∂z=∂L(a,y)∂a∂a∂z其中dz=∂L(a,y)∂zda=∂L(a,y)∂ag′(z)=∂a∂z
dw=dz⋅xdb=dz
(这里我们需要回忆一下sigma函数的导数)
g′(z)=σ′(z)=(11+e−z)′=(11+e−z)(1−11+e−z)=σ(z)(1−σ(z))=a(1−a)(4)(5)(6)(7)(8)
则我们有
dz=da⋅g′(z)=da⋅a(1−a)=(−ya+1−y1−a)⋅a(1−a)=(a−1)y+a(1−y)=a−y(所以我们往往在把两句合成一句写dz=a−y)(9)(10)(11)(12)(13)(14)
而在神经网络中,我们的反向传播是这样的
x↘W[1]→b[1]↗(15)(16)(17)z[1]=W[1]x+b[1]→a[1]=g(z[1])→z[2]=W[2]a[1]+b[2]→a[2]=σ(z[2])→L(a[2],y)
此时我们有
dz[2]=a[2]−ydW[2]=dz[2]a[1]T(这一步与dw=dz⋅x非常像)
这里自己理解一下
dW[2]=∂L∂W[2]=∂L∂z[2]∂z[2]∂W[2]=dz[2]∂z[2]∂W[2](18)(19)(20)
其中值得我们可以思考一下的细节是下面这个应该是什么
∂z[2]∂W[2](21)
我们用一个简单的例子来说明假如第二层有四个节点,而第一层有三个节点:z[2](4,1)=W[2](4,3)a[1](3,1)+b[2](4,1)则有
∂z[2](4,1)∂W[2](4,3)=∂⎡⎢
⎢
⎢⎣z1z2z3z4⎤⎥
⎥
⎥⎦∂⎡⎢
⎢
⎢⎣w11w12w13w21w22w23w31w32w33w41w42w43⎤⎥
⎥
⎥⎦=∂⎡⎢
⎢
⎢⎣w11a1+w12a2+w13a3+b1w21a1+w22a2+w23a3+b1w31a1+w32a2+w33a3+b1w41a1+w42a2+w43a3+b1⎤⎥
⎥
⎥⎦∂⎡⎢
⎢
⎢⎣w11w12w13w21w22w23w31w32w33w41w42w43⎤⎥
⎥
⎥⎦=⎡⎢
⎢
⎢⎣a1a2a3a1a2a3a1a2a3a1a2a3⎤⎥
⎥
⎥⎦=[a1a2a3]=a[2]T(22)(23)(24)(25)(26)
(其实上面的式子只是根据自己理解写出来的,因为查了一系列资料都没有说矩阵对矩阵求偏导的知识)
至此我们完成了反向传播的一半:
dz[2]=a[2]−ydW[2]=dz[2]a[1]Tdb[2]=dz[2]
我们再来进行后半部分,记住下面的这个链
x↘W[1]→b[1]↗(27)(28)(29)z[1]=W[1]x+b[1]→a[1]=g(z[1])→z[2]=W[2]a[1]+b[2]→a[2]=σ(z[2])→L(a[2],y)
则有
da[1]=∂z[2]∂a[1]∂L∂z[2]=W[2]Tdz[2](30)(31)
可能有点难以理解为什么两个偏导的位置要反过来,但其实在此之前我们发现几乎所有的对矩阵求偏导后的结果总是符合这样的规律(参考这篇文章:分子及分母布局)(另外也说明一下我们下面几乎都是用分母布局)或者只是稍稍做了broadcast一下而已,更形象的例子是(以前面举得只有一个隐层的网络为例如下)
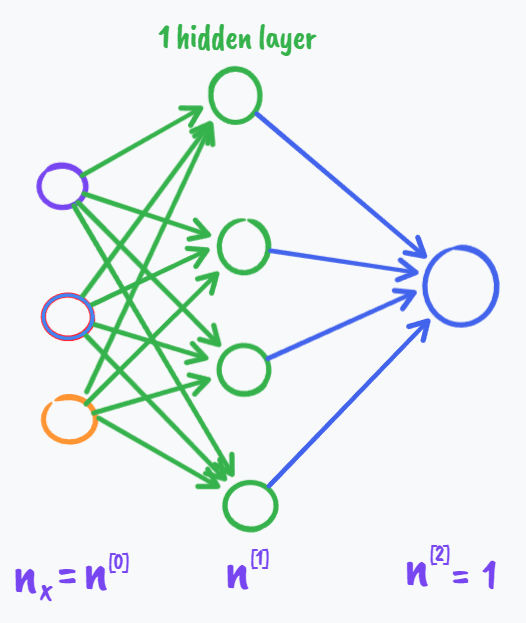 dz[2](1,1)=a[2](1,1)−y(1,1)(z[2]也是(1,1))dW[2](1,4)=dz[2](1,1)⋅a[1]T(1,4)(W[2]也是(1,4)矩阵)db[2](1,1)=dz[2](1,1)(b[2]也是(1,1))da[1](4,1)=W[2]T(4,1)dz[2](1,1)(a[1]也是(4,1)矩阵)
dz[2](1,1)=a[2](1,1)−y(1,1)(z[2]也是(1,1))dW[2](1,4)=dz[2](1,1)⋅a[1]T(1,4)(W[2]也是(1,4)矩阵)db[2](1,1)=dz[2](1,1)(b[2]也是(1,1))da[1](4,1)=W[2]T(4,1)dz[2](1,1)(a[1]也是(4,1)矩阵)
现在我们知道了一个变量导数的维度总是和变量本身的维度是一样的,接下来我们继续进行反向传播,求dz
dz[1]=∂L∂z[1]=∂L∂a[1]∂a[1]∂z[1]=da[1]∗∂g(z[1])∂z[1]=da[1]∗g[1]′(z[1])(32)(33)(34)(35)
注意:这个*号是按元素逐个相乘的意思,因为我们常用的是分母布局,也就很容易了解上面右式中*右边的那个偏导也就是grad,或者说梯度;
dz[1](4,1)=da[1](4,1)∗g[1]′(z[1])(4,1)
而实际应用中我们通常不写出a=……毕竟隐含层我们不太关心,所以可以将上面两步合成一步:
dz[1]=da[1]∗g[1]′(z[1])=W[2]Tdz[2]∗g[1]′(z[1])(36)(37)
更加容易理解的解释是:
dz[1](n[1],1)=W[2]T(n[1],n[2])dz[2](n[2],1)∗g[1]′(z[1])(n[1],1)(38)
根据上面的推导,类似地,我们现在可以很快写出最后两步:
dW[1]=dz[1]xT(dW[1]=dz[1]a[0]T)db[1]=dz[1]
现在我们很容易整理出六个关键的方程,现在把他们都搁这:
dz[2](1,1)=a[2](1,1)−y(1,1)dW[2](1,4)=dz[2](1,1)⋅a[1]T(1,4)db[2](1,1)=dz[2](1,1)dz[1](4,1)=W[2]T(4,1)dz[2](1,1)∗g[1]′(z[1])(4,1)dW[1](4,3)=dz[1](4,1)xT(1,3)db[1](4,1)=dz[1](4,1)
记得我们之前说过这个网络是针对单样本的,所以现在我们要对整个反向传播向量化,即将多样本的叠加起来,就比如z现在就不再是一个列向量而是一个矩阵了现在(在正向传播中我们用过了这种多样本的向量化Vectorizing across multiple examples);
Z[1]=⎡⎢⎣∣∣∣z[1](1)z[1](2)⋯z[1](m)∣∣∣⎤⎥⎦(nz×m)(nz个特征值或节点,m个样本)
如这样:
Z[1]=W[1]X[1]+b[1]
所以对于反向传播,我们也来一次向量化,最终有了开头类似代码的式子:
Backpropagation:dZ[2]=A[2]−YdW[2]=1mdZ[2]A[1]Tdb[2]=1mnp.sum(dZ[1],axis=1,keepdims=True)dZ[1]=W[2]TdZ[2](n[1],m)∗g[1]′(Z[1])(n[1],m)∗是对应元素相乘dW[1]=1mdZ[1]XTdb[1]=1mnp.sum(dZ[1],axis=1,keepdims=True)
需要注意的小细节有这里的求dW时乘以了1/m,这里稍稍解释一下。原因就是当初定义的损失函数:
Costfunction:J(W[1],b[1],W[2],b[2])=1mn∑i=1L(^y,y)
现在我们所求的这个dW是相对所有训练样本而言的,就是说它的列数不受Z或X向量化的影响,依然不变;而它的行数只与特征值有关,我们并没有加入更多的特征,所以行数也是不变的:总体而言,多样本时的W的维度还是和单样本时的维度是一样的。
而我们在求和之后要除与平均值,如果看不出这里的向量化后的矩阵相乘后其实相当于求和,可以再举一下上面那个例子
dz[2](1,1)=a[2](1,1)−y(1,1)dW[2](1,4)=dz[2](1,1)⋅a[1]T(1,4)
向量化之后我们得到了:
dz[2](1,m)=a[2](1,m)−y(1,m)dW[2](1,4)=dz[2](1,m)⋅a[1]T(m,4)
对于dW的第一个元素(第一列),它的值等于dz中所有的元素线性表出之和,其余的元素也类似;而显然,我们需要的dW是针对单样本的(以后检测和test肯定也是针对个别样本去检测和test),所以要去一个平均值即除以m;而对于db也就更明显了,求和后取平均;而对于dZ因为它本身没有进行过求和,所以我们就无需关心它的平均值。
至此,我们学习完了反向传播(随便一搜我们就很容易知道反向传播对深度学习重新火起来多大的作用,这也几乎是非常精彩的一部分),下面我们继续学习参数的影响,需提一句,我们的W全名是weight,即权重,下面我们学习的便是如何初始化我们的权重参数,即随机初始化。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人