Activation functions

基本激活函数

We know that the value of sigmoid function must between 0 and 1. But Andrew said that an activation almost always works better than the sigmoid function and it is the hyperbolic tangent function tanh(x).

$\text{We know that the value of sigmoid function must }\\ \text{between 0 and 1. But Andrew said that an activation }\\ \text{almost always works better than the sigmoid function}\\ \text{and it is the hyperbolic tangent function tanh(x).}\\$

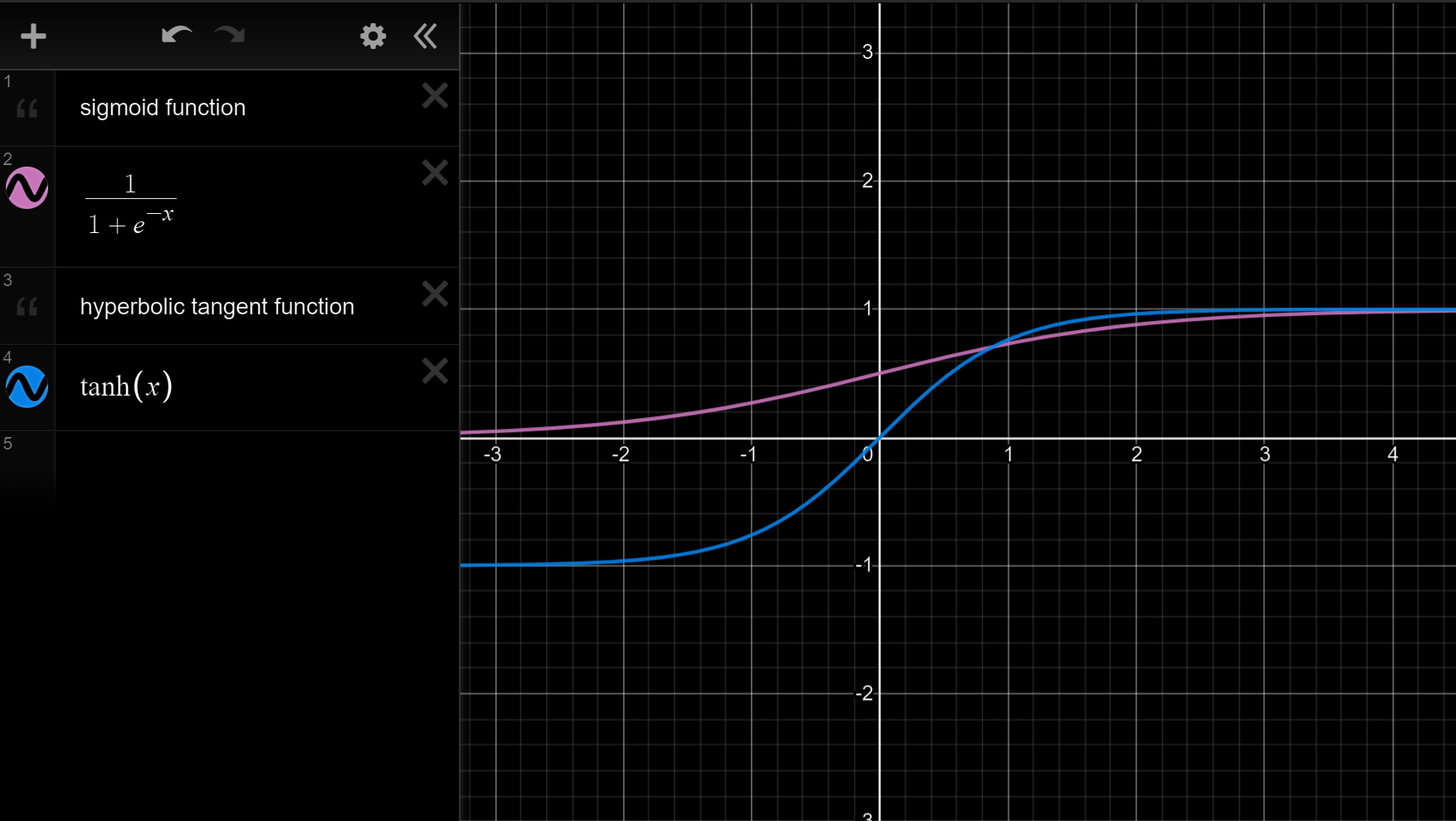I n f a c t, t a n h (x) = \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}} \in (- 1, 1) x \in R

$In\;fact,\\ tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\in(-1,1)\quad x\in\R$

画上图网站Desmos

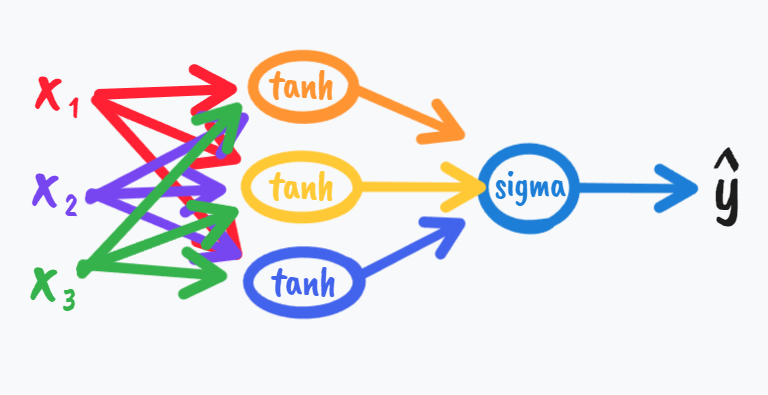
一 般 在 我 们 数 据 中 心 化 的 时 候 我 们 往 往 希 望 平 均 值 为 零 ， 而 不 是 0.5 ， 所 以 这 就 决 定 了 我 们 用 t a n h 的 场 合 可 能 多 于 s i g m a ， 但 是 如 果 回 到 b i n a r y c l a s s i f i c a t i o n, 我 们 就 不 得 不 用 上 s i g m a 了 ， 因 为 显 然 \hat{y} \in (0, 1) 更 加 合 理 ， 我 们 可 以 仅 在 输 出 层 用 到 s i g m a, 而 在 隐 层 都 用 t a n h, 比 如 这 样

$一般在我们数据中心化的时候我们往往希望平均值为零， \\而不是0.5，所以这就决定了我们用tanh的场合可能多于sigma，\\但是如果回到binary\;classification,\\我们就不得不用上sigma了， \\因为显然\hat{y}\in(0,1)更加合理，我们可以仅在输出层用到sigma, \\而在隐层都用tanh,比如这样$

在 这 里 我 们 通 常 会 对 不 同 的 g 加 上 标 表 示 不 同 的 激 活 函 数 ， 如 z^{[1]} = W^{[1]} x + b^{[1]} a^{[1]} = g^{[1]} (z^{[1]}) = \tanh (z^{[1]}) z^{[2]} = W^{[2]} a^{[1]} + b^{[2]} a^{[2]} = g^{[2]} (z^{[1]}) = σ (z^{[1]}) 注 意 细 节 ： 小 写 字 母 是 指 单 个 样 本

$在这里我们通常会对不同的g加上标表示不同的激活函数，如 \\z^{[1]}=W^{[1]}x+b^{[1]} \\a^{[1]}=g^{[1]}(z^{[1]})=\tanh(z^{[1]}) \\z^{[2]}=W^{[2]}a^{[1]}+b^{[2]} \\a^{[2]}=g^{[2]}(z^{[1]})=\sigma(z^{[1]}) \\注意细节：小写字母是指单个样本$

我 们 可 以 知 道 当 z 特 别 大 或 者 特 别 小 时 ， g r a d g 变 得 趋 向 于 0 ， 这 样 往 往 会 “slow down gradient descent” 所 以 在 机 器 学 习 中 我 们 有 这 样 的 方 法 叫 “rectified linear unit” 翻 译 过 来 叫 线 性 修 正 单 元 (R e L U) ， 公 式 为 a = m a x (0, z)

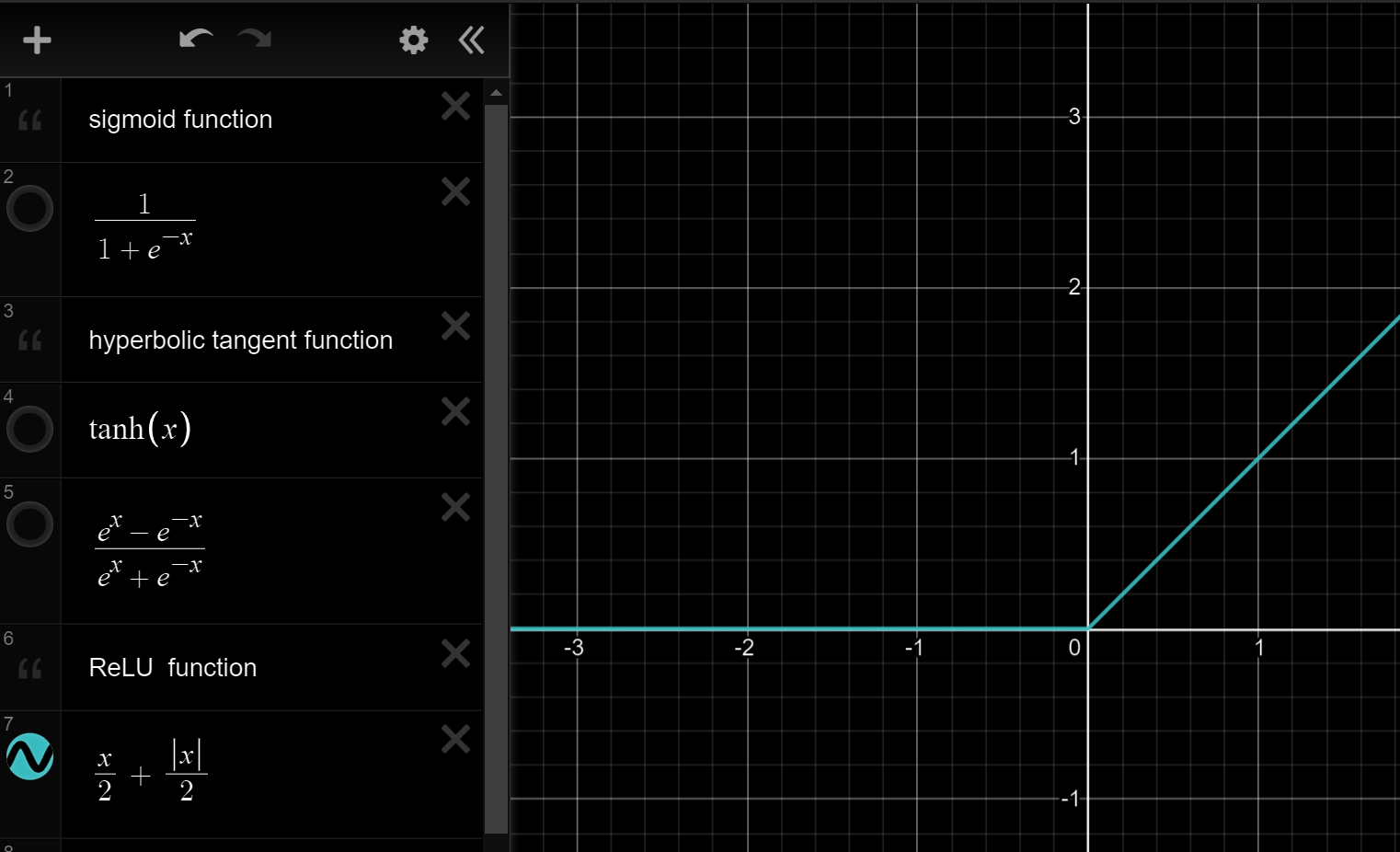
$我们可以知道当z特别大或者特别小时，grad\;g变得趋向于0，\\这样往往会\text{“slow down gradient descent”}\\ 所以在机器学习中我们有这样的方法叫\text{“rectified linear unit”}\\翻译过来叫线性修正单元(ReLU)，公式为a=max(0,z)$

实 际 上 上 面 这 个 函 数 是 不 可 微 的 ， 我 们 也 知 道 有 一 半 范 围 的 值 为 零 但 是 只 要 有 足 够 多 的 样 本 使 z > 0, 那 我 们 总 体 上 就 对 大 多 数 训 练 样 本 还 是 挺 快 的 所 以 上 面 所 提 及 到 的 b i n a r y c l a s s i f i c a t i o n ， 我 们 可 以 把 这 样 改 (A n d r e w 说 的 r u l e s o f t h u m b (经 验 法 则)) ： 在 o u t p u t l a y e r 用 σ, 而 在 h i d d e n l a y e r 用 我 们 的 R e L U, 像 这 样 ：

$实际上上面这个函数是不可微的，我们也知道有一半范围的值为零 \\但是只要有足够多的样本使z>0,那我们总体上就对大多数训练样本还是挺快的 \\所以上面所提及到的binary\;classification，我们可以把这样改(Andrew说的rules\;of\;thumb(经验法则))： \\在output\;layer用\sigma,而在hidden\;layer用我们的ReLU,像这样：$

则目前我们学习了四个激活函数：

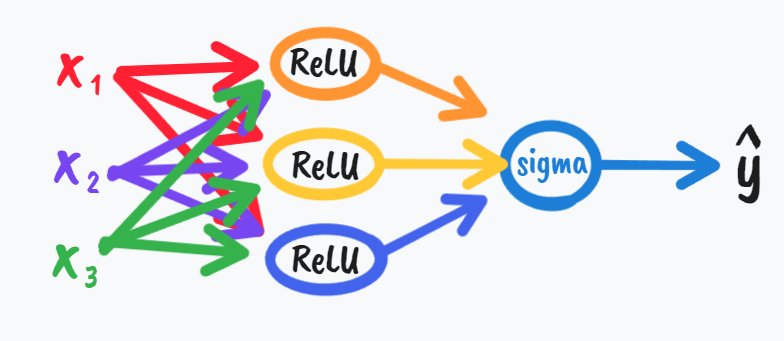
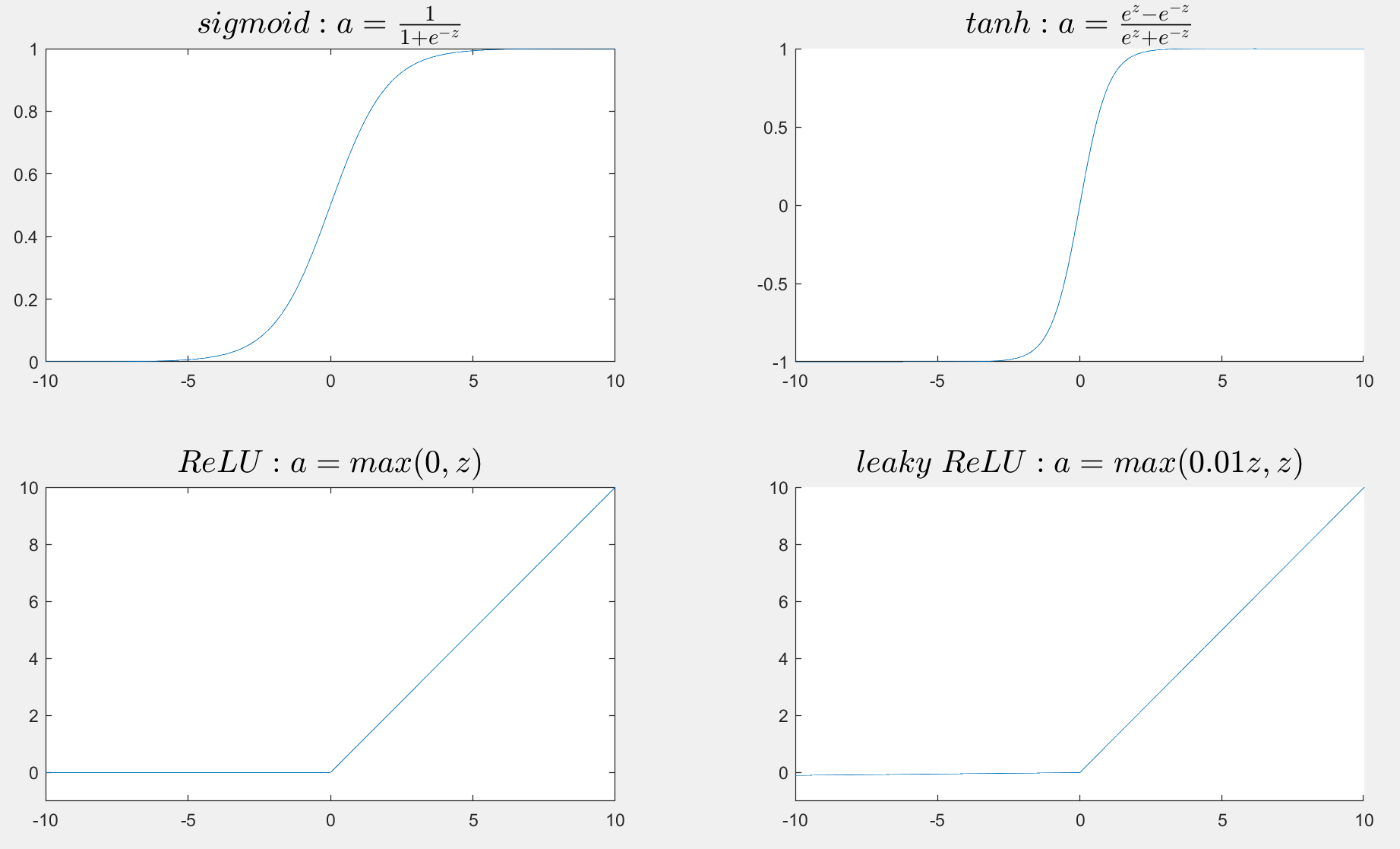
其中leaky是渗漏的意思，就是让小于零那一部分z还可以起到小小的作用🌹。而其中ReLU是不知道用啥时所用到的激活函数，事实上对于激活函数，或者对于函数中的细节改进，或者对于hidden layer中的单元数我们有很多种不同的选择，这也增大了我们的难度或者说是尝试的机会，或者像Andrew说的一样，you know try them all and then evaluate on like a holdout validation set.

接下来我们学习为什么需要非线性函数的原因：

z^{[1]} = W^{[1]} x + b^{[1]} a^{[1]} = g^{[1]} (z^{[1]}) z^{[2]} = W^{[2]} a^{[1]} + b^{[2]} a^{[2]} = g^{[2]} (z^{[2]}) 通 常 在 上 面 这 个 式 中 ， 如 果 我 们 有 g^{[1]} (z^{[1]}) = z^{[1]} 我 们 有 时 称 它 为 l i n e a r a c t i v a t i o n f u n c t i o n; 更 好 的 名 字 应 该 是 i d e n t i t y a c t i v a t i o n f u n c t i o n (恒 等 激 活 函 数) 如 果 我 们 在 每 一 层 都 只 用 这 种 线 性 激 活 函 数 的 话 ， 我 们 容 易 想 到 \begin{aligned} (1) & a^{[2]} & = W^{[2]} a^{[1]} + b^{[2]} \\ (2) & = W^{[2]} (W^{[1]} x + b^{[1]}) + b^{[2]} \\ (3) & = (W^{[2]} W^{[1]}) x + (W^{[2]} b^{[1]} + b^{[2]}) \\ (4) & = W^{'} x + b^{'} \end{aligned} 最 后 得 出 的 \hat{y} 也 不 过 是 x 的 线 性 组 合 的 结 果 ， \hat{y} = W^{'} x + b^{'} 就 相 当 于 是 直 接 建 立 x 与 \hat{y} 的 关 系 ， 这 样 我 们 还 不 如 去 掉 隐 藏 层 （ 它 在 这 里 没 有 如 何 意 义 ）

$\\z^{[1]}=W^{[1]}x+b^{[1]} \\a^{[1]}=g^{[1]}(z^{[1]}) \\z^{[2]}=W^{[2]}a^{[1]}+b^{[2]} \\a^{[2]}=g^{[2]}(z^{[2]}) \\通常在上面这个式中，如果我们有g^{[1]}(z^{[1]})=z^{[1]} \\我们有时称它为linear\;activation\;function; \\更好的名字应该是identity\;activation\;function(恒等激活函数) \\如果我们在每一层都只用这种线性激活函数的话，我们容易想到 \\ \begin{align} a^{[2]}&=W^{[2]}a^{[1]}+b^{[2]} \\&=W^{[2]}(W^{[1]}x+b^{[1]})+b^{[2]} \\&=(W^{[2]}W^{[1]})x+(W^{[2]}b^{[1]}+b^{[2]}) \\&=W'x+b' \end{align} \\最后得出的\hat{y}也不过是x的线性组合的结果， \\\hat{y}=W'x+b' \\就相当于是直接建立x与\hat{y}的关系，这样我们还不如去掉隐藏层（它在这里没有如何意义）$

我们刚刚证明了如果隐藏层中都用线性激活函数和没有隐藏层的网络是等价的，所以既然我们建立了所谓的神经网络，就更加应该去让每一层的传播变得有意义起来，如果这里需要用到线性，我们可以把它交给参数W决定就好，而无需单独多建一层隐藏层，（其实没有隐藏层相当于回到了机器学习中的线性回归问题），到这里我们也就明白了为什么需要非线性激活函数的存在了。

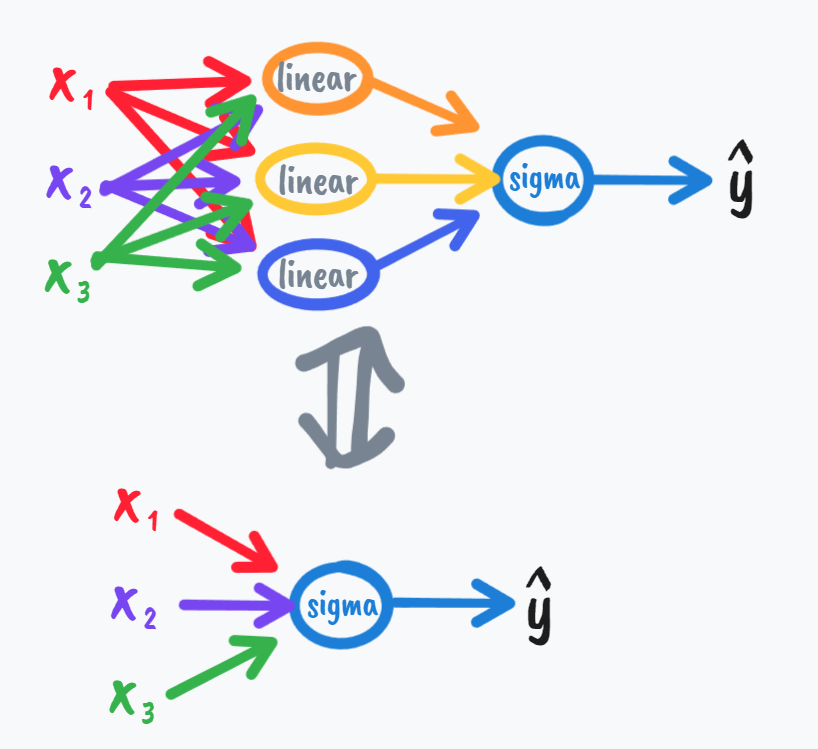
最后，笔者谈一下自己看法：其实我们更应该从物理层面去思考内在的激活函数关系，就好比六个对应自由度的值可以输出一个刚体的位姿，其内在肯定存在一个激活函数的模型，而不是建立很多隐层建立很多单元去逼近它，因为这样总是存在不能完全拟合的缺点，而且试错的快慢也需要由物质条件决定，但在现阶段难以得到更好结果的情况下用这种试错方法算是局部最优化了，我们好像也找不出理由不学习它。

激活函数的slope(斜率)和derivative(导数)

S i g m o i d a c t i v a t i o n f u n c t i o n : g (x) = σ (x) = \frac{1}{1 + e^{- x}} \frac{d}{d x} g (x) = \frac{- e^{- x}}{(1 + e^{- x})^{2}} = \frac{1}{1 + e^{- x}} (1 - \frac{1}{1 + e^{- x}}) = g (x) (1 - g (x)) 若 a = g (z), g^{'} (z) = a (1 - a)

$Sigmoid\;activation\;function: \\g\left(x\right)=\sigma(x)=\frac{1}{1+e^{-x}} \\\frac{d}{dx}g\left(x\right)=\frac{-e^{-x}}{(1+e^{-x})^2}=\frac{1}{1+e^{-x}}(1-\frac{1}{1+e^{-x}})=g(x)(1-g(x)) \\若a=g(z),g'(z)=a(1-a)$

T a n h a c t i v a t i o n f u n c t i o n : g (x) = t a n h (x) = \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}} \frac{d}{d x} g (x) = \frac{(e^{x} + e^{- x})^{2} - (e^{x} - e^{- x})^{2}}{(e^{x} + e^{- x})^{2}} = \frac{4}{(e^{x} + e^{- x})^{2}} = 1 - (t a n h (x))^{2} 若 a = g (z), g^{'} (z) = 1 - a^{2}

$Tanh\;activation\;function: \\g\left(x\right)=tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \\\\\frac{d}{dx}g\left(x\right)= \frac{(e^{x}+e^{-x})^2-(e^{x}-e^{-x})^2}{(e^{x}+e^{-x})^2} =\frac{4}{(e^{x}+e^{-x})^2}=1-(tanh(x))^2 \\若a=g(z),g'(z)=1-a^2$

R e L U a n d L e a k y R e L U : g (z) = m a x (0, z) g^{'} (z) = {\begin{cases} 1 & if z > 0 \\ 0 & if z < 0 \\ u n d e f i n e d & if z = 0 \end{cases} (但 事 实 上 z = 0 处 的 导 数 为 0 或 1 都 是 没 有 影 响 的 ， 这 在 我 们 后 面 训 练 数 据 的 时 候 可 以 看 到) 在 实 践 中 人 们 喜 欢 这 样 定 义 (影 响 不 大) ： g^{'} (z) = {\begin{cases} 0 & if z < 0 \\ 1 & if z \geq 0 \end{cases} g (z) = m a x (0.01 z, z) g^{'} (z) = {\begin{cases} 0.01 & if z < 0 \\ 1 & if z \geq 0 \end{cases}

$ReLU\;and\;Leaky\;ReLU: \\g(z)=max(0,z) \\g'(z)= \begin{cases} 1 & \text{ if } z>0 \\ 0 & \text{ if } z<0 \\ undefined & \text{ if } z=0\\ \end{cases} \\(但事实上z=0处的导数为0或1都是没有影响的，这在我们后面训练数据的时候可以看到) \\在实践中人们喜欢这样定义(影响不大)： \\g'(z)= \begin{cases} 0 & \text{ if } z<0 \\ 1 & \text{ if } z\ge 0 \\ \end{cases} \\g(z)=max(0.01z,z) \\g'(z)= \begin{cases} 0.01 & \text{ if } z<0 \\ 1 & \text{ if } z\ge 0 \\ \end{cases}$

画图matlab源代码

>> clear
>> 
>> syms x;
>> clear
>> syms z;
>> a=sigma(z);
索引超出数组元素的数目(1)。

出错 sigma (line 96)
  a=varargin{1}; b=varargin{2}; c=varargin{3}; d=varargin{4};
 
>> a=1/(1+e^(-z));
函数或变量 'e' 无法识别。
 
>> a=1/(1+exp^(-z));
错误使用 exp
输入参数的数目不足。
 
>> a=1/(1+exp(1)^(-z));
>> fplot(z)
>> plot(a,z)
错误使用 plot
数据必须为可转换为双精度值的数值、日期时间、持续时间或数组。% 老错误，plot不支持syms
 
>> clear
>> z=-2:0.01:2;
>> a=1/(1+exp(1)^(-z));
错误使用  ^  (line 51)
用于对矩阵求幂的维度不正确。请检查并确保矩阵为方阵并且幂为标量。要执行按元素矩阵求幂，请使用 '.^'。
 
>> 
>> a=1/(1+exp(1).^(-z));
错误使用  / 
矩阵维度必须一致。
 
>> a=1./(1+exp(1).^(-z));
>> plot(z)
>> 
>> plot(a)
>> z=-10:0.1:10;
>> a=1./(1+exp(1).^(-z));
>> plot(a)
>> plot(a)
>> subplot(2,2,1)
>> plot(a)
>> 
title('$\frac{sin(x)}{x}$','interpreter','latex', 'FontSize', 18); % 插入latex公式的方法
>> title('$sigmoid:a=\frac{1}{1+e^{-z}}$','interpreter','latex', 'FontSize', 18);
>> axis auto
>> plot(z,a)
>> subplot(2,2,2)
>> title('$tanh:a=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$','interpreter','latex', 'FontSize', 18);
>> hold on;
>> subplot(2,2,1)
>> title('$sigmoid:a=\frac{1}{1+e^{-z}}$','interpreter','latex', 'FontSize', 18);
>> subplot(2,2,2)
>> a1=(exp(1).^(z)-exp(1).^(-z))/(exp(1).^(z)+exp(1).^(-z));
>> a1=(exp(1).^(z)-exp(1).^(-z))./(exp(1).^(z)+exp(1).^(-z));
>> plot(z,a1)
>> subplot(2,2,3)
>> title('$ReLU:a=max(0,z)$','interpreter','latex', 'FontSize', 18);
>> subplot(2,2,2)
>> title('$tanh:a=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}$','interpreter','latex', 'FontSize', 18);
>> a2=z./2+abs(z).2;
 a2=z./2+abs(z).2;
               ↑
错误: 表达式无效。请检查缺失的乘法运算符、缺失或不对称的分隔符或者其他语法错误。要构造矩阵，请使用方括号而不是圆括号。
 
是不是想输入:
>> a2=z./2+abs(z)./2;
>> subplot(2,2,3)
>> plot(z,a2)
>> axis([-10,10,-10,10])
>> axis([-1,10,-10,10])
>> axis([-10,10,-1,10])
>> subplot(2,2,4)
>> title('$leaky\;ReLU:a=max(0.01z,z)$','interpreter','latex', 'FontSize', 18);
>> hold on
>> subplot(2,2,3)
>> title('$ReLU:a=max(0,z)$','interpreter','latex', 'FontSize', 18);
>> hold on
>> subplot(2,2,4)
>> a3=1.01.*z./2+abs(0.99.*z)./2;
>> plot(z,a3)
>> axis([-10,10,-1,10])