Vectorizing across multiple examples
Vectorizing across multiple examples
\[So\; given\; input:\;x\\
\begin{align}
\mathop{z^{[1]}}\limits_{(4,1)}
&=\mathop{W^{[1]}}\limits_{(4,3)}
\mathop{x}\limits_{(3,1)}
+\mathop{b^{[1]}}\limits_{(4,1)}\\
\rightarrow
\mathop{a^{[1]}}\limits_{(4,1)}
&=\sigma(\mathop{z^{[1]}}\limits_{(4,1)})\\
\rightarrow
\mathop{z^{[2]}}\limits_{(1,1)}
&=\mathop{W^{[2]}}\limits_{(1,4)}
\mathop{a^{[1]}}\limits_{(4,1)}
+\mathop{b^{[2]}}\limits_{(1,1)}\\
\rightarrow
\mathop{a^{[2]}}\limits_{(1,1)}
&=\sigma(\mathop{z^{[2]}}\limits_{(1,1)})\\
\end{align}
\]
在上次学习中,我们主要推导上面这四条公式
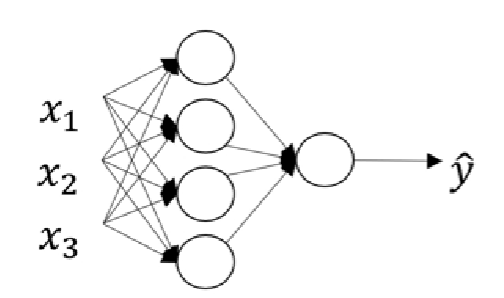
图1.单个样本
这个图就是我们计算单个样本的输出时所用到的,现在我们需要重复多次这种运算,所以我们首先想到的肯定还是向量化:
\[对于单个样本我们有\\
x\rightarrow a^{[2]}=\hat{y}\\
所以对于m个样本,我们有\\
\begin{array}{c}
x^{(1)}&\rightarrow &a^{[2](1)} = \hat{y}^{(1)}\\
x^{(2)}&\rightarrow &a^{[2](2)} = \hat{y}^{(2)}\\
\vdots &\rightarrow &\vdots \\
x^{(m)}&\rightarrow &a^{[2](m)} = \hat{y}^{(m)}\\
\end{array}\\
在这里,我们容易知道\\x是一个样本,同时也是个n\times1的向量\\
而x^{(1)},x^{(2)},\cdots,x^{(m)}则表示我们有m个这种样本\\
(解释一下a^{[2](i)}的[\;^{[2]}]表示第二层,而[\;^{(i)}]则表示对应第i个样本)\\
很容易想到后面我们可以把他们一列一列地放在一起组成一个n\times m的矩阵\\
\]
如果我们用for-loops去一个个样本执行时,我们可以这样(伪代码)
\[for\;i=1\;to\;m:\\
\begin{align}
z^{[1](i)} & = W^{[1]}x^{(i)}+b^{[1]}\\
a^{[1](i)} & = \sigma(z^{[1](i)})\\
z^{[2](i)} & = W^{[2]}a^{[1](i)}+b^{[2]}\\
a^{[2](i)} & = \sigma(z^{[2](i)})\\
\end{align}
\]
我们把m个样本x向量化后记为X
\[X=\begin{bmatrix}
\mid & \mid &&\mid \\
x^{(1)} & x^{(2)} &\cdots &x^{(m)}\\
\mid & \mid &&\mid
\end{bmatrix}
\\
(n_x,m)\\
注:n_x指的时x中的数据数目
\]
所以我们去写代码时应该是这样
\[\begin{align}
Z^{[1]} & = W^{[1]}X+b^{[1]}\\
A^{[1]} & = \sigma(Z^{[1]})\\
Z^{[2]} & = W^{[2]}A^{[1]}+b^{[2]}\\
A^{[2]} & = \sigma(Z^{[2]})\\
\end{align}
\]
里面的Z同样
\[Z^{[1]}=\begin{bmatrix}
\mid & \mid &&\mid \\
z^{[1](1)} & z^{[1](2)} &\cdots &z^{[1](m)}\\
\mid & \mid &&\mid
\end{bmatrix}
\\(n_z,m)\\
A^{[1]}=\begin{bmatrix}
\mid & \mid &&\mid \\
a^{[1](1)} & a^{[1](2)} &\cdots &a^{[1](m)}\\
\mid & \mid &&\mid
\end{bmatrix}
\\(n_z,m)\\
注:容易知道n_z不一定等于n_x,但n_a=n_z
\]
对于我们刚刚所提到的矩阵,我们可以画个这样的图:

到目前为止,我们可以得到一个在神经网络中正向传播的向量化实现,下面我们将对其进一步解释:
我们不妨假设只有三个样本,而且还是应用上面那个神经网络:
\[X^{[1]}=\begin{bmatrix}
\mid & \mid &\mid \\
x^{[1](1)} & x^{[1](2)} &x^{[1](3)}\\
\mid & \mid &\mid
\end{bmatrix}
\\
z^{[1](1)}=W^{[1]}x^{[1](1)}+b^{[1]}\\
\rightarrow
\mathop{\begin{bmatrix}
\;\cdot\; \\
\cdot \\
\cdot \\
\cdot \\
\end{bmatrix}}\limits_{(1)}
=\begin{bmatrix}
\cdot&\cdot&\cdot \\
\cdot&\cdot&\cdot \\
\cdot&\cdot&\cdot\\
\cdot&\cdot&\cdot\\
\end{bmatrix}
\mathop{\begin{bmatrix}
\;\cdot\; \\
\cdot \\
\cdot \\
\end{bmatrix}}\limits_{(1)}
+
\begin{bmatrix}
\;\cdot\; \\
\cdot \\
\cdot \\
\cdot \\
\end{bmatrix}\\
Z^{[1]}=W^{[1]}X^{[1]}+b^{[1]}\\
\rightarrow
\begin{bmatrix}
\mathop{\begin{bmatrix}
\;\cdot\; \\
\cdot \\
\cdot \\
\cdot \\
\end{bmatrix}}\limits_{(1)}
\mathop{\begin{bmatrix}
\;\cdot\; \\
\cdot \\
\cdot \\
\cdot \\
\end{bmatrix}}\limits_{(2)}
\mathop{\begin{bmatrix}
\;\cdot\; \\
\cdot \\
\cdot \\
\cdot \\
\end{bmatrix}}\limits_{(3)}
\end{bmatrix}=
\begin{bmatrix}
\cdot&\cdot&\cdot \\
\cdot&\cdot&\cdot \\
\cdot&\cdot&\cdot\\
\cdot&\cdot&\cdot\\
\end{bmatrix}
\begin{bmatrix}
\mathop{\begin{bmatrix}
\;\cdot\; \\
\cdot \\
\cdot \\
\end{bmatrix}}\limits_{(1)}
\mathop{\begin{bmatrix}
\;\cdot\; \\
\cdot \\
\cdot \\
\end{bmatrix}}\limits_{(2)}
\mathop{\begin{bmatrix}
\;\cdot\; \\
\cdot \\
\cdot \\
\end{bmatrix}}\limits_{(3)}
\end{bmatrix}
+\begin{bmatrix}
\cdot&\cdot&\cdot \\
\cdot&\cdot&\cdot \\
\cdot&\cdot&\cdot\\
\cdot&\cdot&\cdot\\
\end{bmatrix}
\\注:由于广播b的每一列应该都是一样的
\]
由矩阵相乘的知识我们容易知道这是对的,这样,我们也就直观解释了这样向量化的原因;
下面一章我们继续学习不同激活函数的作用,除了sigmoid函数,我们应该也有更好的激活函数。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号