A quick overview of neural network of Andrew Ng
A quick overview of neural network of Andrew Ng
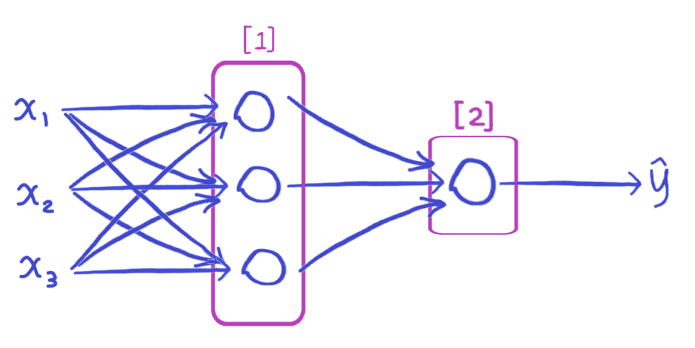
图1.简单的概览
\[对于[1],我们有\\
\rightarrow z^{[1]}=W^{[1]}x+b^{[1]}
\rightarrow a^{[1]}=\sigma(z^{[1]})\\
对于[2],我们有\\
\rightarrow z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}\rightarrow
a^{[2]}=\sigma(z^{[2]})\;(\hat{y}=a^{[2]})\\
\rightarrow\mathcal{L} (a^{[2]},y)
\]
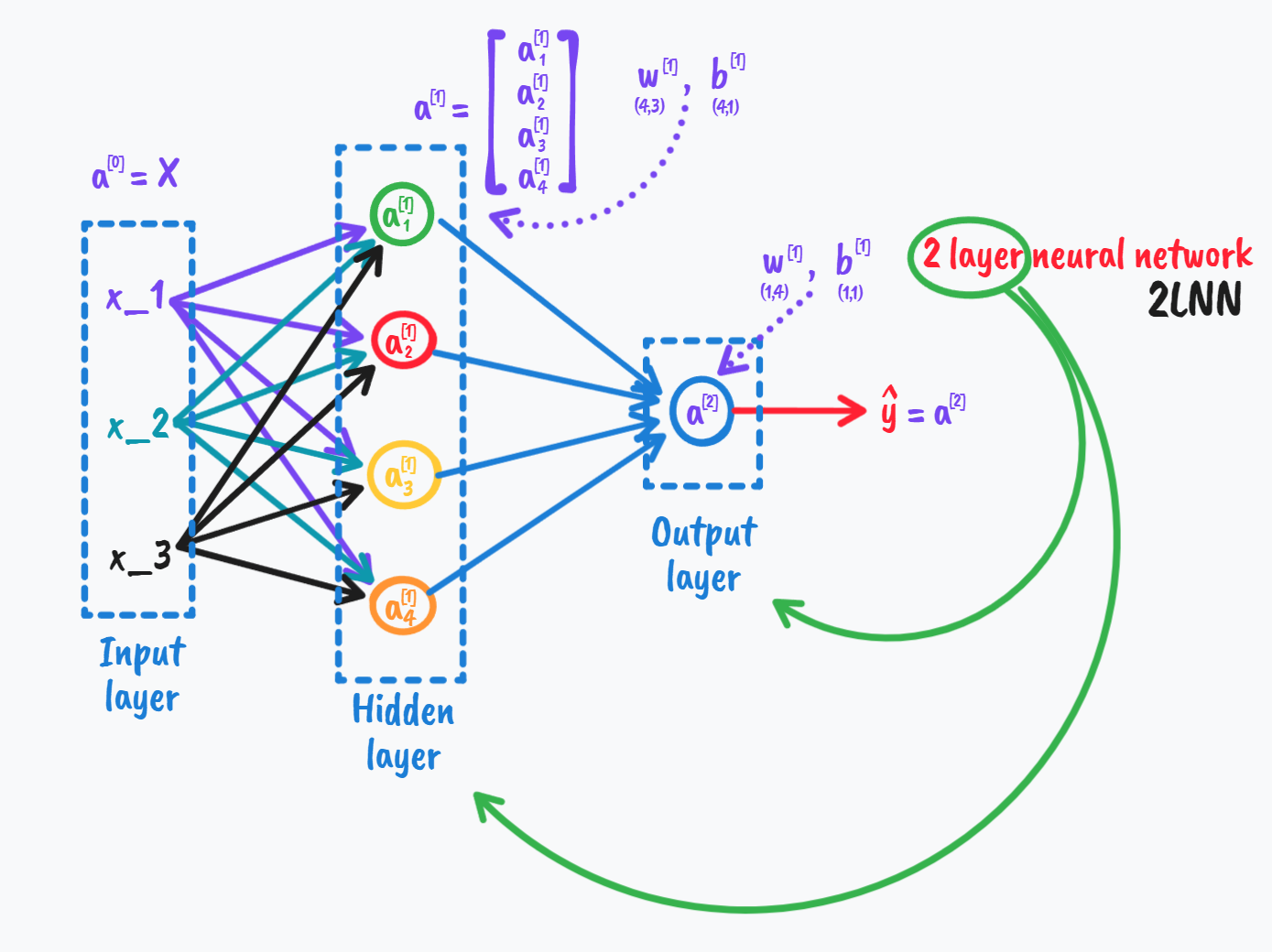
图2.上面这幅图代表了很多东西，得花时间理解。
我们分析网络中的第一层第一个节点：
\[z^{[1]}_1=w^{[1]T}_1x+b^{[1]}_1\\
a^{[1]}_1=\sigma(z^{[1]}_1)\\
\quad(上标[^{\;[1]}]代表的是这些变量只和第一个隐层有关，下标[_{\;1}]表示第1个节点)
\]
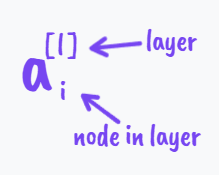
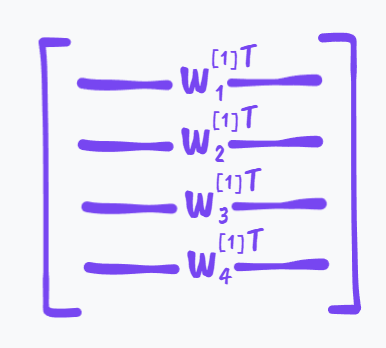
图3.这个矩阵显然是4×3的矩阵
这样我们也容易理解图二中w下方的（4,3）所代表的意思了，即W是一个4×3的矩阵，同理b是一个4×1，所以下面标着（4,1）。
\[我们知道w^{[1]}_i本来是一个3×1的向量，\\把w^{[1]}_i向量化(且转置)之后成为了一个1×3的向量，(所以横着放)，\\这样我们容易有\\
\begin{bmatrix}
w^{[1]T}_1 \\
w^{[1]T}_2 \\
w^{[1]T}_3 \\
w^{[1]T}_4
\end{bmatrix}
\cdot
\begin{bmatrix}
x_1\\
x_2\\
x_3
\end{bmatrix}+\begin{bmatrix}
b^{[1]}_1\\
b^{[1]}_2\\
b^{[1]}_3\\
b^{[1]}_4
\end{bmatrix}
=\begin{bmatrix}
w^{[1]T}_1 X+b^{[1]}_1\\
w^{[1]T}_2 X+b^{[1]}_2\\
w^{[1]T}_3 X+b^{[1]}_3\\
w^{[1]T}_4 X+b^{[1]}_4
\end{bmatrix}
=\begin{bmatrix}
z^{[1]}_1\\
z^{[1]}_2\\
z^{[1]}_3\\
z^{[1]}_4
\end{bmatrix}
=Z^{[1]}
\]
需要注意的是我们总习惯把变量定义为列向量（如果不加说明就默认是列向量），比如里面的X是一个3×1的向量，后面的Z是一个4×1的向量；
\[X=\begin{bmatrix}
x_1&x_2&x_3
\end{bmatrix}^T
\]
再得到a,
\[a^{[1]}=
\begin{bmatrix}
a^{[1]}_1\\
\vdots \\
a^{[1]}_4
\end{bmatrix}
=\sigma(z^{[1]})
\]
\[So\; given\; input:\;x\\
\begin{align}
\mathop{z^{[1]}}\limits_{(4,1)}
&=\mathop{W^{[1]}}\limits_{(4,3)}
\mathop{x}\limits_{(3,1)}
+\mathop{b^{[1]}}\limits_{(4,1)}\\
\rightarrow
\mathop{a^{[1]}}\limits_{(4,1)}
&=\sigma(\mathop{z^{[1]}}\limits_{(4,1)})\\
\rightarrow
\mathop{z^{[2]}}\limits_{(1,1)}
&=\mathop{W^{[2]}}\limits_{(1,4)}
\mathop{a^{[1]}}\limits_{(4,1)}
+\mathop{b^{[2]}}\limits_{(1,1)}\\
\rightarrow
\mathop{a^{[2]}}\limits_{(1,1)}
&=\sigma(\mathop{z^{[2]}}\limits_{(1,1)})\\
\end{align}
\]
观察上面式子的底标我们可以发现里面的规律挺有意思的,另外x也可以被当成第零层的数据而写成：
\[x=a^{[0]}
\]
另外这里的W不同于我们上面的w,应该是这样
\[W^{[1]}=w^{[1]T}\\
W^{[2]}=w^{[2]T}
\]
回到我们最开始的
\[z=w^Tx+b\\
\hat{y}=a=\sigma{(z)}
\]
我们实现the output of logistic regression同样只需要上面那四行代码即可，
至此我们完成了一个样本的output,下面我们学习多样本的向量化。
所用画图工具：🥀
