第二周周末学习下matlab

Matlab学习之周末

🔎目前学习资源：R2020a

请先自行从各大免费资源网址下载安装好

🔑建议学习时间：

学习解析几何或者学习线性代数时同步学习

目录

第一天学习

数组：
行向量&列向量&转置&矩阵&特殊数组
x1=[a b c d e f]
x2=[a,b,c,d,e,f] % x2=x1
x3=[a;b;c;d;e;f] % x3=x2' 转置
x4=[a,b,c;d,e,f]
% define another array
x=m:n % (m,m+1,m+2,...,n)
x=m:k:n % (m,m+k,m+2k,...,n)
x=linspace(m,n,k) % (m,m+(n-m)/(k-1),m+2(n-m)/(k-1),...,n)即在[m,n]上k-1等分，一共有k个元素
数组与标量运算
x=[a,b,c,d,e]
% 加减乘除
% x+q=[a+q,b+q,c+q,...]
% x*q=[a*q,b*q,c*q,...]
% x/q=[a/q,b/q,c/q,...]
% x.\q=[q/a,q/b,q/c,...]
% 幂运算
% x.^q=[a^q,b^q,c^q,...]
% q.^x=[q^a,q^b,q^c,...]
数组与数组运算
x=[a,b,c,d];
y=[e,f,g,h];
% x+y=[a+e,b+f,...]
% x.*y=[a*e,b*f,...]
% x./y=[a/e,b/f,...]这才是除号
% x.\y=[e/a,f/b,...]
% x.^y=[a^e,b^f,...]
注释：
crtl+R注释，crtl+L取消
[x,y]=meshgrid(-20:1:20);
z=2*x-3*y;
mesh(x,y,z);
% hold on;
xlabel('x');
ylabel('y');
zlabel('z');
产生特殊矩阵
a=eye(m,n) 
% m*n 单位矩阵 a=eye(2,4)->a=[1 0 0 0;0 1 0 0]
b=zeros(m,n) % m*n 零矩阵
矩阵元素操作
（提取，删除，合并）
>> a=[1 2 3 4;
5 6 7 8;
9 10 11 12]

a =

     1     2     3     4
     5     6     7     8
     9    10    11    12

>> a(1:2 3:4)
 a(1:2 3:4)
       ↑
错误: 表达式无效。请检查缺失的乘法运算符、缺失或不对称的分隔符或者其他语法错误。要构造矩阵，请使用方括号而不是圆括号。% 想表达的是没有逗号
 
>> a(1:2,3:4) % 提取部分矩阵

ans =

     3     4
     7     8
     
>> a(1:2,:) % 提取部分行

ans =

     1     2     3     4
     5     6     7     8
     
>> a(:,3:4) % 提取部分列

ans =

     3     4
     7     8
    11    12
     
>> c=[1;3;5]

c =

     1
     3
     5

>> [a,c] %列合并

ans =

     1     2     3     4     1
     5     6     7     8     3
     9    10    11    12     5
% 注如果纬度不一致会这样提示：错误使用 horzcat要串联的数组的维度不一致。
>> d=[1,2,3,4]

d =

     1     2     3     4

>> [a;d] %行合并

ans =

     1     2     3     4
     5     6     7     8
     9    10    11    12
     1     2     3     4
矩阵运算
>> A=[1,2;3,4]

A =

     1     2
     3     4

>> B=[4,5;6,7]

B =

     4     5
     6     7

>> A+B

ans =

     5     7
     9    11

>> A*B

ans =

    16    19
    36    43

>> det(A) % 行列式

ans =

    -2

>> inv(A) % 逆矩阵

ans =

   -2.0000    1.0000
    1.5000   -0.5000

>> A/B % 矩阵右除 X*B=A的解

ans =

    2.5000   -1.5000
    1.5000   -0.5000

>> A\B % 矩阵左除 A*X=B的解

ans =

   -2.0000   -3.0000
    3.0000    4.0000
循环
for循环
>> clear %清空此前的变量赋值
>> s=0;
>> for i=1:50; %执行50次
s=s+i;
end %循环休止
>> s

s =

        1275


>> for n=1:6;
x(n)=sin(pi/n);
end
>> x(1) %输出结果说明了精确度有多小，而我们还是期待为零

ans =

   1.2246e-16

>> x

x =

    0.0000    1.0000    0.8660    0.7071    0.5878    0.5000

>> x(2)

ans =

     1
while循环
>> clear
>> m=4.5;
>> cnt=0;
>> while m<5
cnt=cnt+1
m=m*1.03
end

cnt =

     1


m =

    4.6350


cnt =

     2


m =

    4.7740


cnt =

     3


m =

    4.9173


cnt =

     4


m =

    5.0648
if-else-end
function f=fdhs(x) %分段函数简写
if x<0
    f=2*x+sin(x)
end
if x>=0
    f=exp(x)-1
end

>> fdhs(3)

f =

   19.0855


ans =

   19.0855


function f=fdhs(x)
if x<0
    f=2*x+sin(x)
elseif x>=0&x<=1
    f=exp(x)-1
elseif x>1
    f=2
end %这个函数其实也可以写成几个if-end

第二天学习

绘图
plot：输出单条线
plot(x,y,'S') % S为线的形状

>> x=[0:0.01:2*pi];
>> y=sin(x);
>> plot(x,y) %在这之后会输出实线
>> plot(x,y,'--')

image

plot：输出多条线
>> x=[0:0.01:2*pi];
>> y1=sin(x+pi/6);
>> y2=sin(x+pi/3);
>> y3=sin(x+pi/2);
>> plot(x,y1,'^',x,y2,'*',x,y3)

image

ezplot
>> ezplot('sin(t)',[0,2*pi])
%ezplot('f(x)',[a,b])
%y=f(x)在[a,b]上的图像

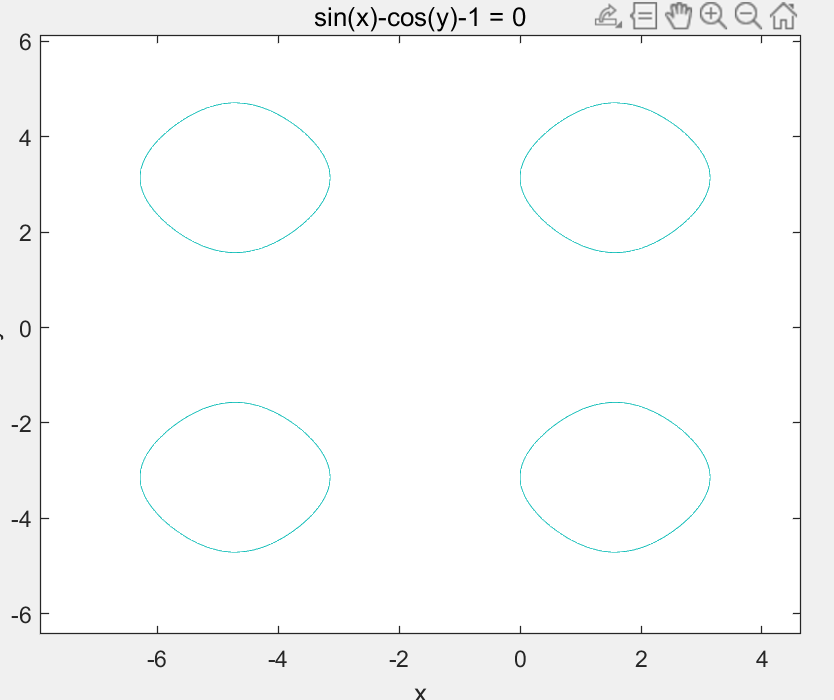
image

>> ezplot('sin(x)-cos(y)-1',[-2*pi,2*pi,-2*pi,2*pi])
%ezplot('f(x,y)',[a,b,c,d])
%f(x,y)=0在x属于[a,b]上，y属于[c,d]上的图像

image

ezplot('x(t)','y(t)',[a,b])

上面这些都是定义二维的

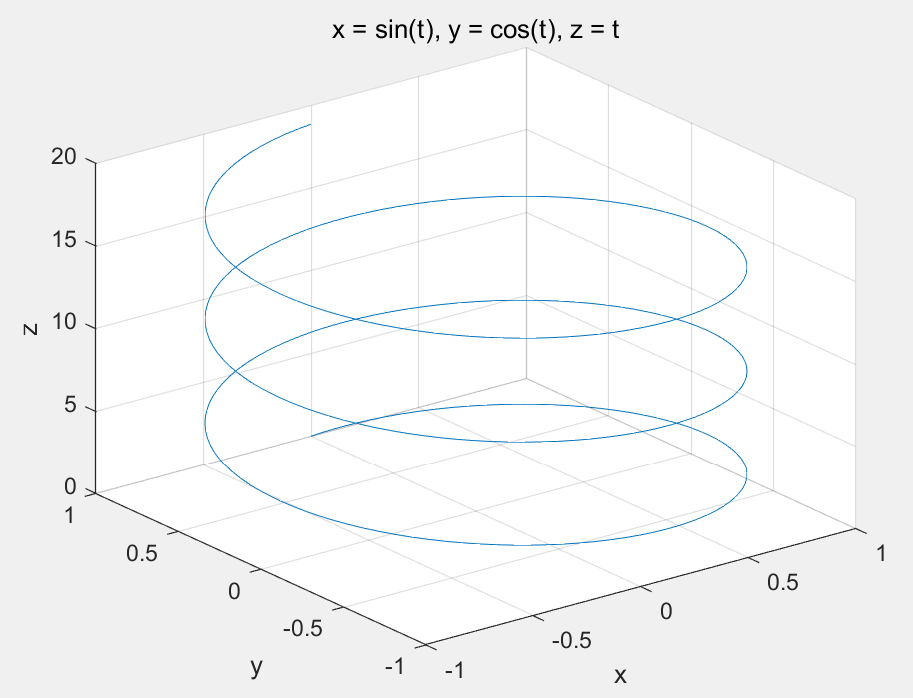
>> ezplot3('sin(t)','cos(t)','t',[0,6*pi])
%三维参数方程，最后一个参数是范围

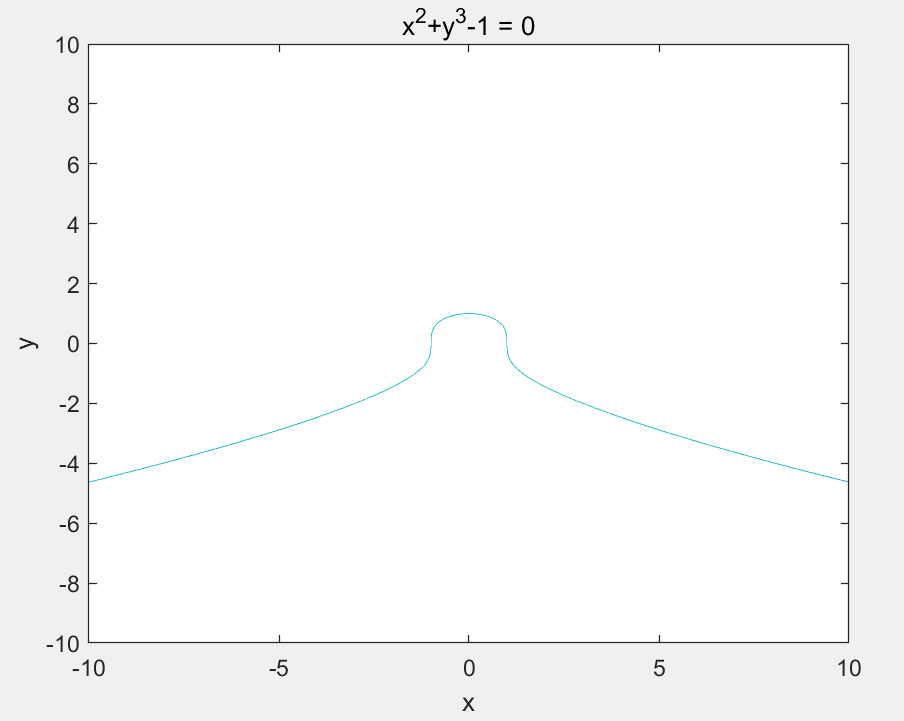
image

>> ezplot('x.^2+y.^3-1',[-10,10,-10,10])
%这里之所以用.^是因为x、y是个数组array

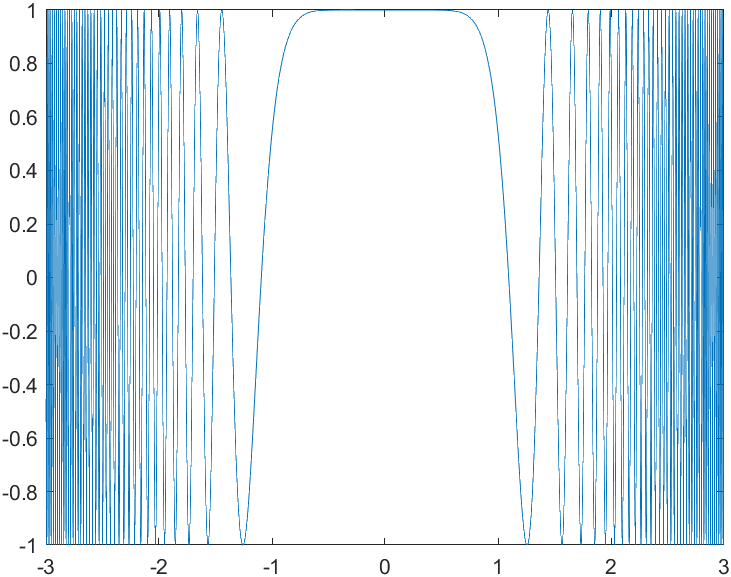
image

fplot
function f=fdhs(x)
f=cos(x.^5)

上面这段保存在fdhs.m文件里

命令行运行

fplot('fdhs',[-3,3])

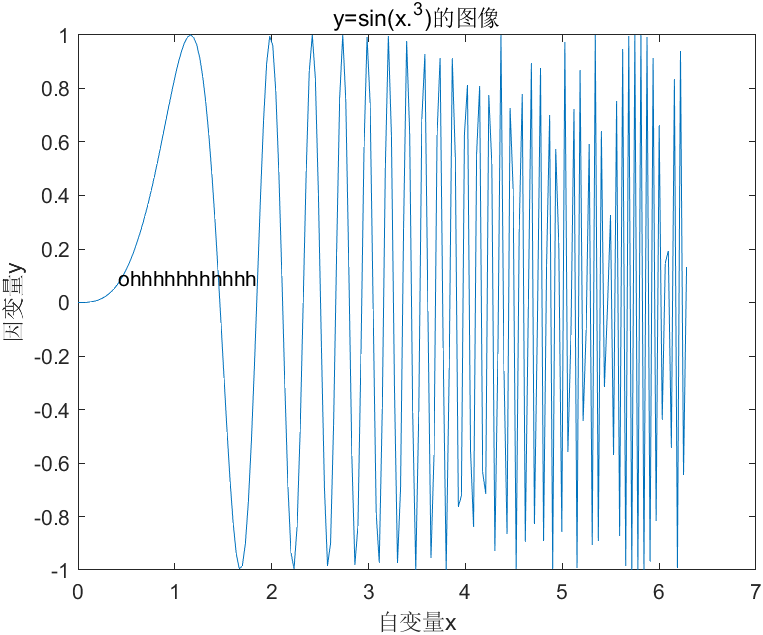
image

添加标注
>> x=[0:pi/100:2*pi];
>> y=sin(x.^3);
>> plot(x,y)
>> xlabel('自变量x')
>> ylabel('因变量y')
>> title('y=sin(x.^3)的图像')
>> gtext('ohhhhhhhhhhh') %这个输入之后会等待你在图上放置标注内容

image

添加网格、调整图像坐标系、分割图像窗口

命令行输入（注：下面的输入都是接着添加标注的代码一起的）

>> grid on %开启
>> grid off %关闭
>> axis([1,2,-1,0]) %只显示该区域
>> axis auto %恢复缺省设置
>> subplot(2,2,1);
>> plot(x,y)
>> subplot(2,2,2);
>> plot(x,y)
>> axis(4,6,-1,0) %这里报错是因为没有定义成数组的形式（也叫向量）
错误使用 axis>LocSetLimits (line 319)
向量必须包含 4、6 或 8 个元素。

出错 axis (line 114)
                LocSetLimits(ax(j),cur_arg,names);
 
>> axis([4,6,-1,0])
>> subplot(2,2,3);
>> plot(x,y)
>> axis([4,6,0,1])
>> subplot(2,2,4)
>> plot(x,y)
>> axis([0,6,0,1])
>> title('图像4')
>> subplot(2,2,1) %这里纯粹是由于忘记加图题了，发现重新调用就还可以对图像进行操作
>> title('图像1')
>> subplot(2,2,2);
>> title('图像2')
>> subplot(2,2,3);
>> title('图像3')

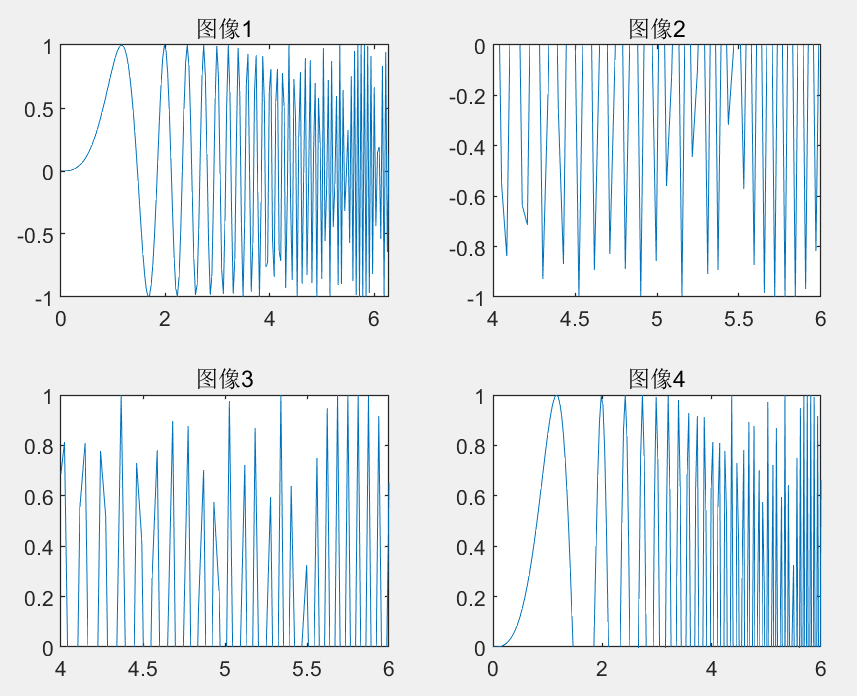
image

绘图2
极坐标
>> theta=0:0.1:2*pi;
>> r=3*(1+cos(theta));
>> polar(theta,r)

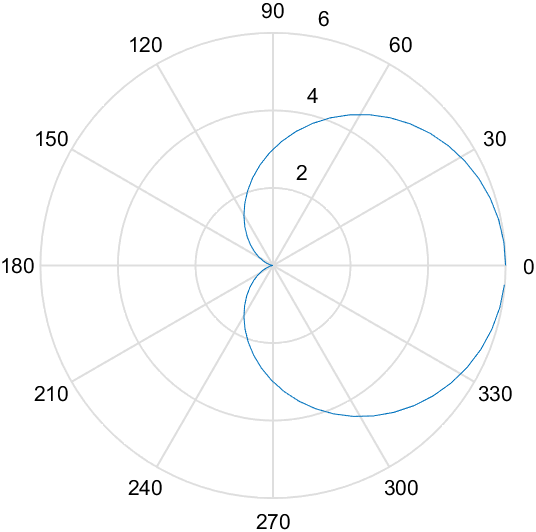
image

theta = 0:0.01:2*pi;
rho = sin(2*theta).*cos(2*theta);

figure
polar(theta,rho,'--b')

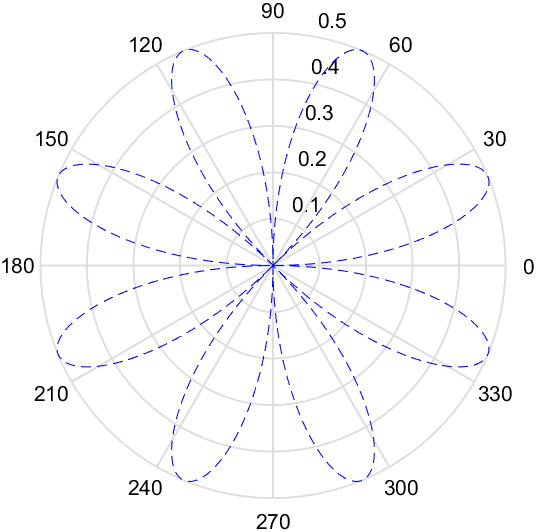
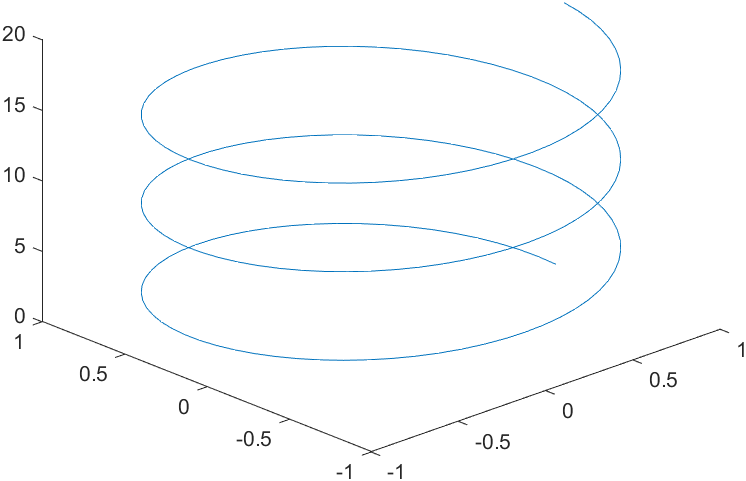
image

plot3：一条三维曲线(以老师说的螺旋线为例)
>> polar(theta,rho,'--b')
>> clear
>> t=0:0.1:6*pi;
>> x=cos(t);
>> y=sin(t);
>> z=t;
>> plot3(x,y,z)

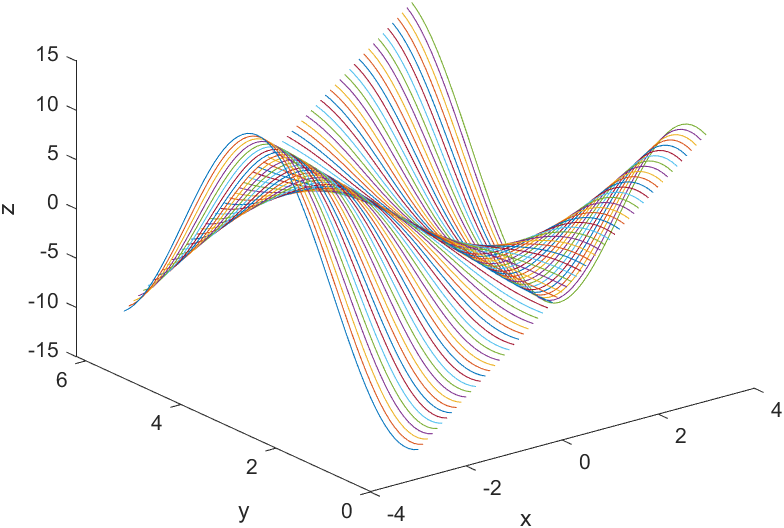
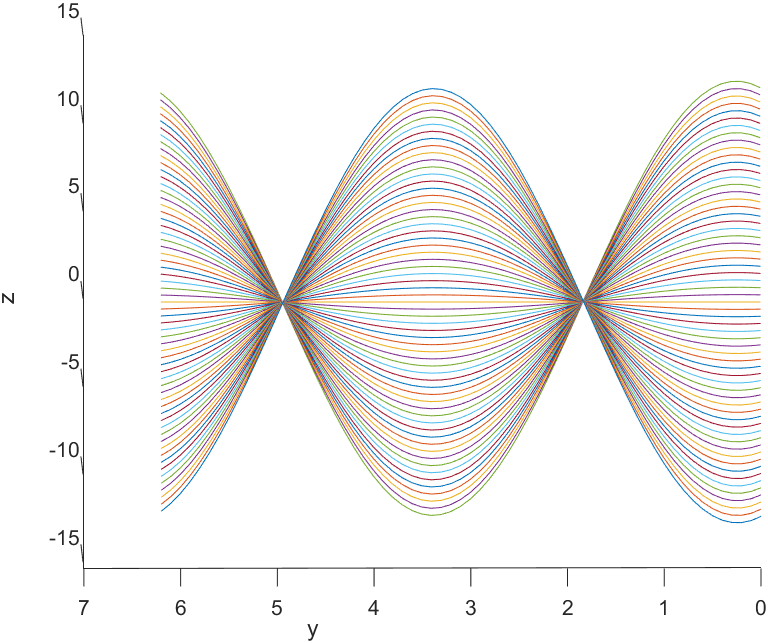
image

plot3：多条三维曲线
>> x=-3:0.1:3;
>> y=0:0.1:2*pi;
>> [x,y]=meshgrid(x,y);
>> z=x.*sin(y)+4*x.*cos(y); %由下面坐标可知x方向上是离散的，也正好说明了此式的意义，也不难发现yoz平面上的投影是连续不平行的，而其它两个平面上的投影是离散的，且线与线之间是平行的。
>> plot3(x,y,z)
>> ylabel('y')
>> xlabel('x')
>> zlabel('z')

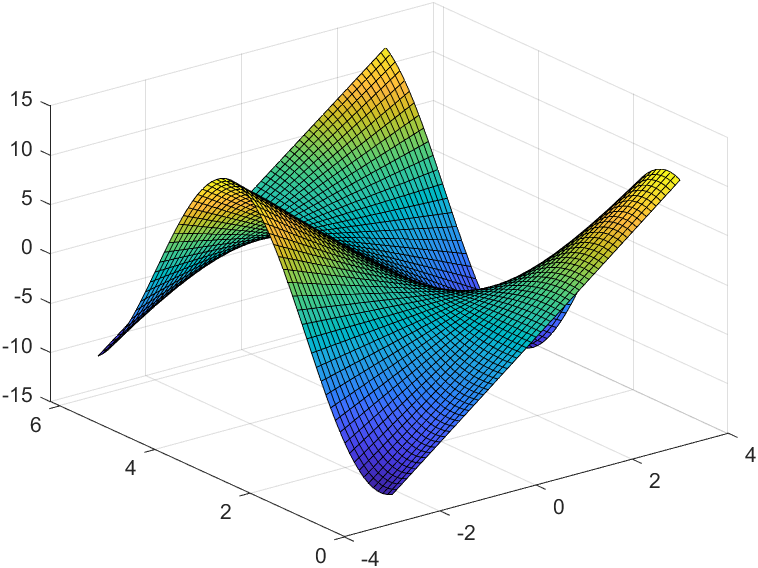
image
image

🏄surf:三维曲面
>> surf(x,y,z) %接着plot3那段一起来的

image

>> shading flat %图像平滑

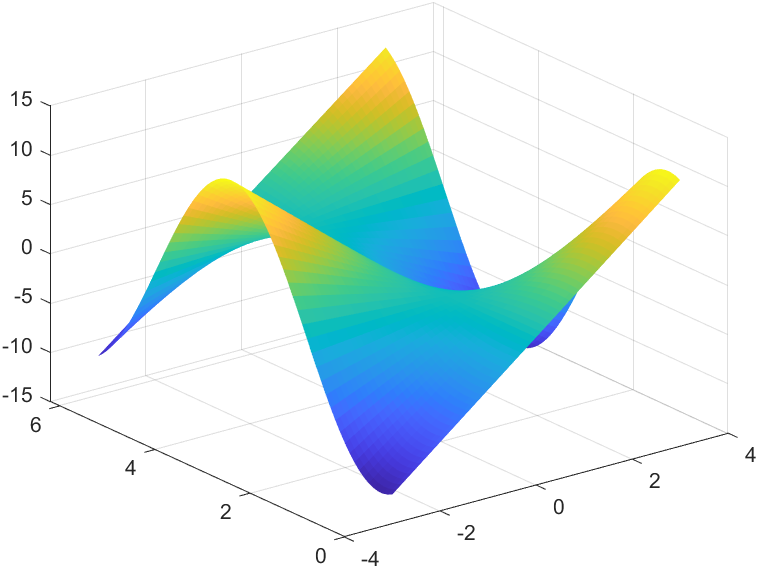
image

🍖mesh
>> mesh(x,y,z) %网格图
>> meshz(x,y,z) %带参考平面

image

💢其它
>> meshc(x,y,z) %带等高线
>> surfc(x,y,z) %带等高线
>> surface(x,y,z) %xoy面上投影，带颜色
绘制散点图
>> plot(x,y,'k') %绘制散点并连线
>> scatter(x,y,'k') %绘制散点

周末学习总结

matlab这东西只能说应该是每个学生都应该掌握的本领，它在很多领域都有非常大的作用，这篇学习笔记介绍的只是很小的一部分内容且没有广度也没有深度，但这也是目前作者所能初步学习到的知识了，放在这里与大家一起学习，另外有关于基本绘图函数的更多信息。

🥀

posted @ 2022-03-06 13:01  Link_kingdom  阅读(463)  评论(0)  编辑  收藏  举报