数学相关
质数理论及筛法相关
质数判断（Miller-Rabbin 算法）
首先根据费马小定理，对于一个质数 \(p\)，有 \(\forall a \in [1, p - 1]\)，\(a ^ {p - 1} \equiv 1 (\bmod \ p)\)。但是假设需要判断的数为 \(n\)，随机挑选一个数 \(a\)，并且判断 \(a ^ {n - 1} \equiv 1(\bmod \ n)\) 成功，却不一定成立。这种数叫做卡迈克尔数。
于是有两种提高准确度的方法：
-
选择更多的 \(a\) 进行多次尝试，每次都检验 \(a ^ {n - 1} \equiv 1 (\bmod \ n)\) 是否成立。
-
使用二次探测定理。
二次探测定理：若有 \(x ^ 2 \equiv 1 (\bmod \ p)\)，则有 $x \equiv 1 (\bmod \ p) $ 或 \(x \equiv p - 1 (\bmod \ p)\)。
因此，如果当前的探测因子 \(a\) 满足了 \(a ^ {n - 1} \equiv 1 (\bmod \ n)\)（此时无法证明 \(n\) 是质数），那么可以继续探测是否满足 \(a ^ {\frac{n - 1}{2}} \equiv 1 (\bmod \ n)\) 或者 \(a ^ {\frac{n - 1}{2}} \equiv n - 1 (\bmod \ n)\)，一直如此进行下去。
因此可以写出一个 \(O(s \log ^ 2 n)\) 的代码：
bool MillerRabbin(int n) {
for (int p : tst) {
if (n == p) return 1;
else if (p > n) return 0;
int cnt = qpow(p, n - 1, n);
if (cnt != 1) return 0;
int now = n - 1;
while (!(now & 1) and cnt == 1) {
now >>= 1; cnt = qpow(p, now, n);
if (cnt != 1 and cnt != n - 1) return 0;
}
} return 1;
}
其中 tst 表示探测因子数组。
接下来继续对算法进行优化。发现复杂度瓶颈在快速幂。可以用 double 处理的 \(O(1)\) 快速幂来代替。另外一种方法则更加简便：首先将 \(n - 1\) 写成 \(t \times 2 ^ k\) 的形式。然后先判断 \(t\) 是否成立，然后把 \(t\) 自乘 \(k\) 次，每次都判断一下。这样只需要用到乘法，因此复杂度降掉一个 \(\log\)。
bool MillerRabbin(int n) {
if (n == 1) return 0;
int t = n - 1, k = 0;
while (!(t & 1)) t >>= 1, k ++ ;
for (int p : tst) {
if (n == p) return 1;
int a = qpow(p, t, n), ne = a;
rep(i, 1, k) {
ne = 1ll * a * a % n;
if (ne == 1 and a != 1 and a != n - 1) return 0;
a = ne;
} if (a != 1) return 0;
} return 1;
}
质数筛法
欧拉筛法：对于每个合数只筛其最小的因数。复杂度 \(O(n)\)。
void get_prime(int n) {
for (int i = 2; i <= n; i ++ ) {
if (!st[i]) q[ ++ cnt] = i;
for (int j = 1; j <= cnt && i * p[j] <= n; j ++ ) {
st[i * p[j]] == 1; if (i % p[j] == 0) break;
}
}
}
通常可以筛某些神奇的函数，其满足积性函数性质，或者与其最小质因子强相关。
约数个数和约数和
-
唯一分解定理：每个数 \(n \in N ^*\) 都可以被唯一分解成 \(\prod p_i ^ {c_i}\)。
-
约数个数和：\(\prod (c_i +1)\)。每个质因子可以选 \(0 \sim c_i\) 个。
-
约数和：\(\prod \dfrac{p_i ^ {c_i + 1} - 1}{p_i - 1}\)。道理与约数个数和相同，只不过换上了等比数列求和。
min-25 筛
解决函数 \(f\) 的前缀和问题。
下文中的一些记号：
-
\(F(n) = \sum_{i = 1}^{n} f(i)\)：\(f(i)\) 的前缀和。
-
\(\text{lp}(n)\)：\(n\) 的最小质因子。
-
\(p_k\)：全体质数中第 \(k\) 小的质数。
-
\(\dfrac{x}{y}\)：默认下取整。
首先尝试解决这个问题：求出
其中 \(m \in \{\dfrac{n}{1}, \dfrac{n}{2}, \dfrac{n}{3} \cdots , \dfrac{n}{n}\}\)，一共有 \(\sqrt n\) 中取值。
考虑 dp。设 \(g(j, m)\) 表示：
也就是对于所有的质数或者最小质因数大于 \(p_j\) 的 \(f'\) 求和。
这里的 \(f'\) 需要满足下面的三个性质：
-
\(\forall p \in P, f'(p) = f(p)\)。
-
\(f'\) 是完全积性函数。
-
\(\sum f'\) 可以快速求值。
初始时，\(g(0, m) = \sum_{2 \le i \le m} f'(i)\)。
转移时分两种情况：
-
若 \(p_j ^ 2 > m\)：\(g(j, m) = g(j - 1, m)\)。因为不存在 \(i \in [1, m]\)，使得 \(\text{lp}(i) > p_j\)。
-
若 \(p_j ^ 2 \le m\)：
这个式子怎么理解呢？首先，这里可以理解成从 \(g(j - 1, m)\) 里面筛掉所有 \(\text{lp} = p_j\) 的 \(f'\) 值。而筛掉的值一定可以表示成 \(p_j \times q\)，其中 \(q\) 是一个 \(\le \dfrac{m}{p_j}\) 而且最小质因子 \(\le p_j\) 的数。最后减掉的那块，是 \(g(j - 1, \dfrac{m}{p_j})\) 里面的那部分质数。由于 \(f'\) 是完全积性函数，这两部分可以直接相乘。
以上部分时间复杂度被证明是 \(O(\dfrac{n ^ {0.75}}{\log n})\)。
上面求出了 \(G(m) = \sum_{i \in P, i \le m} f(i) = g(\pi(m), m)\)。
同余相关
最大公约数和最小公倍数
-
最大公约数（\(\gcd(a, b)\)），也写作 \((a, b)\)，是最大的 \(d\) 满足 \(d | a\) 且 \(d | b\)。
-
设 \(a = \prod p_i ^ {c_i}, b = \prod q_i^{d_i}\)，则 \(d = \prod_{P \in \{p\} or \{q\}} \min(c_i, d_i)\)。
-
神奇 trick：\(n\) 不同的数按一定顺序求 \(\gcd\)，\(O(\log V)\) 次之后变为 \(1\)。
-
最小公倍数，记作 \([a, b]\)，满足 \([a, b] (a, b) = ab\)。
bonus：最大公约数的二进制优化：
最大公约数求解过程中，如果两个数都有很多 \(2\) 的因子，那么就会浪费很多时间。二进制优化最大公约数基于下面的原理：
-
\(a\) 为偶数，\(b\) 为偶数：\(\gcd(a, b) = \gcd(\frac{a}{2}, \frac{b}{2}) \times 2\)。
-
\(a\) 为偶数，\(b\) 为奇数：\(\gcd(a, b) = \gcd(\frac{a}{2}, b)\)。
-
\(a\) 为奇数，\(b\) 为偶数：与上面同理。
-
\(a, b\) 都为奇数：只能朴素求了。
int gcd(int a, int b) {
int i = 0, j = 0;
if (!a || !b) return a + b;
for (; !(a & 1); i ++ , a >>= 1);
for (; !(b & 1); j ++ , b >>= 1);
if (i > j) i = j;
while (true) {
if (a < b) swap(a, b);
if ((a -= b) == 0) return b << i;
while ((a & 1) == 0) a >>= 1;
}
}
该算法可以用于除法及其慢的情况，如高精 \(\gcd\)。
扩展欧几里得算法 exgcd
考虑不定方程
令 \(x' \leftarrow y, y' \leftarrow x - \left \lfloor \dfrac{a}{b} \right \rfloor y\) 之后迭代即可。
有两种不同写法，一种写法是按照上述规则模拟：
int exgcd(int &x, int &y, int a, int b) {
if (!b) { x = 1, y = 0; return a; }
int d = exgcd(x, y, b, a % b);
int tx = x, ty = y;
x = ty, y = tx - (a / b) * ty;
return d;
}
另一种方式在每次迭代的时候将 \(x, y\) 翻转，这样可能更加简洁。
int exgcd(int &x, int &y, int a, int b) {
if (!b) { x = 1, y = 0; return a; }
int d = exgcd(y, x, b, a % b);
y -= (a / b) * x; return d;
}
\(\text{tips:}\)
- 求 \(ax + by = c\) 的方程的一组解：
假设 \(ax + by = (a, b) = d\) 的一组解为 \(x_0, y_0\)，则 \(ax_0 \times \dfrac{c}{d} + by_0 \times \dfrac{c}{d} = (a, b) \times \dfrac{c}{d} = c\)。
因此得到一组解 \(x = x_0 \times \dfrac{c}{d}, y = y_0 \times \dfrac{c}{d}\)。
- 求 \(ax + by = c\) 的所有解。
通过构造可以得到，若 \(x_0, y_0\) 为方程的一组解，则 \(x = x_0 + \dfrac{b}{(a, b)}, y = y_0 - \dfrac{a}{(a, b)}\) 也是方程的一组解。可以证明，所有解都可以表示成
的形式。
- 求 \(ax + by = c\) 的所有正整数解。
利用通解的公式容易求得（\(x, y\) 增减性相反）。
乘法逆元
用于进行模意义下的乘法。\(a\) 的乘法逆元记作 \(a ^ {-1}\)。根据定义 \(a \times a ^ {-1} \equiv 1 (\bmod \ p)\)
-
求单个值 \(a\) 的乘法逆元：
-
通过 \(\text{exgcd}\)。发现就是解 \(ax \equiv 1 (\bmod \ p)\) 的解。可以直接用 \(\text{exgcd}\) 解同余方程。
-
通过费马小定理。
费马小定理：对于质数 \(p\) 和一个与其互质的数 \(a\)，一定满足 \(a^{p - 1} \equiv 1 (\bmod \ p)\)。
证明：\(\forall a \in (0, p), a \in N^*, ka \ \bmod p\) 互不相同（\(k = 0, 1 \cdots p - 1\)）。因此 \((p - 1)! a = 1a \times 2a \cdots (p - 1)a \equiv (p - 1)! (\bmod \ p)\)。因此 \(a^{p - 1} \equiv 1 (\bmod \ p)\)
所以得到 \(a^{p - 1} \times a ^ {-1}\equiv a^{p - 2} \equiv a^{-1} (\bmod \ p)\)。快速幂求出 \(a^{p - 2}\) 即可。
int qpow(int a, int b = mod - 2) {
int s = 1; for (; b; b >>= 1, a = 1ll * a * a % mod)
if (b & 1) s = 1ll * s * a % mod; return s;
}
- 求 \(1 \sim n\) 中所有正整数阶乘的逆元。
首先线性预处理出所有正整数的阶乘。然后用扩欧或者快速幂求出所有阶乘的逆元。这样做的复杂度是 \(O(n \log n)\)。
然后发现可以这样搞：首先求出 \(n!\) 的逆元。然后倒推，对于所有 \((i !) ^ {-1}\)，其都等于 \([(i + 1)!]^{-1} \times (i +1)\)。因此可以线性求出。
线性求阶乘逆元常应用于组合数学。
- 求 \(1 \sim n\) 中所有正整数的逆元：
首先线性求所有阶乘逆元。然后发现，对于数字 \(a\)，其逆元 \(a^{-1} = (a !) ^{-1} \times (a - 1)!\)。可以做到线性。
- 求一堆数的逆元：
首先需要把整除 \(p\) 的所有数拎出来单独处理。显然他们的逆元都是 \(0\)。
接下来处理所有数的前缀积，记为 \(pre_i\)。对 \(pre_n\)，用快速幂求逆元。
可以倒推出所有前缀积的逆元：\(pre\_inv_i = pre\_inv_{i + 1} \times a_i\)。
最后可以用前缀积和前缀积的逆元推出每个数的逆元。时间复杂度也是 \(O(n)\)。
中国剩余定理
本来应该先学中国剩余定理的。但是有了扩展中国剩余定理，朴素的 CRT 就没用了。
扩展中国剩余定理用来求解如下形式的同余方程组：
扩展中国剩余定理的基本思想是合并，通过 \(n - 1\) 次合并，将一个大的同余方程组合并成一个同余方程。
假设现在有两个同余方程：
现在要将他们合并。首先转化成不定方程：
成功转化成了系数为 \((A, -B, b - a)\) 的不定方程，使用 exgcd 求出他的一个根。因此转化成了一个同余方程：\(x \equiv Ak_1 + a (\bmod \ \text{lcm}(A, B))\)。合并完成。
// 合并 x = a(mod A), x = b(mod B) 两个方程
// 返回的是新的 a', b'，满足 x = a'(mod b')
PII merge(int a, int A, int b, int B) {
int k1, k2; int d = exgcd(k1, k2, A, B);
k1 = k1 * (b - a) / d;
int p = A / d * B; return {(A * k1 + a) % p, p};
}
bonus：
- 如果 \(x\) 的系数不为 \(1\)。
也就是 P4774 [NOI2018] 屠龙勇士。
求解形如：
Excrt 因为 \(x\) 的系数是一，因此可以直接联立两个不定方程。也尝试将这个东西转化成不定方程的形式。假设现在需要合并的两个同余方程是：
然后发现两个 \(x\) 的系数不同，不能直接合并了。而这两个柿子两边又不能同时除以 \(p\) 或者 \(P\)，因为不保证逆元存在。这就非常难搞。
一个神奇的思路是直接解出两个方程。以第一个方程为例，方程中只有两个未知数 \(x\) 和 \(-k_1\)，可以解出一个特解 \(x_0\)。那么所有 \(x\) 就可以表示成：
同理解第二个方程，可以得到
我们惊奇的发现这两个 \(x\) 的系数相同了。所以可以合并一下：
里面只有 \(\alpha, \beta\) 两个未知数，解出他们两个就可以得到 \(x\)。
- 扩展中国定理进行模数非质数的合并
即 古代猪文。
求 \(\dbinom{n}{m} \bmod \ 999911658\) 的值。
将 \(999911658\) 质因数分解得到：\(999911658 = 2 \times 3 \times 4679 \times 35617\)。
因此可以对 \(2, 3, 4679, 35617\) 分别做一遍 \(\text{Lucas}\)，得到下面的同余方程：
可以直接用 excrt 合并一下。
另外一个应用是扩展卢卡斯。其基本思路也是将模数拆成若干质因数的次方，计算后 excrt 合并。
积性函数及系理论
如果一个数论函数 \(f\) 对于任意的 \(n \bot m\) 都满足 \(f(nm) = f(n)f(m)\)，则称 \(f\) 是一个积性函数。
积性函数可以使用筛法来求。后面会写。
欧拉函数
欧拉函数定义为：\(\varphi(n)\) 表示 \(1 \sim n\) 中所有与 \(n\) 互质的数的个数。
关于欧拉函数有下面的性质和用途：
-
欧拉函数是积性函数。可以通过这个性质求出他的公式。
-
\(f(p) = p - 1\)。很显然，比质数 \(p\) 小的所有数都与他互质。
-
\(f(p ^ 2) = p \times (p - 1)\)。显然，对于这 \(p ^ 2\) 个数，只有 \(p, 2p, 3p \cdots p ^ 2\) 不与 \(p ^ 2\) 互质。
-
\(f(p ^ k) = p ^ {k - 1}(p - 1)\)。
-
假设 \(n = \prod^k p_i ^ {c_i}\)，则 \(f(n) = \prod^k f(p_i ^ {c_i}) = \prod^k p_k ^ {c_k - 1}(p_k - 1) = n \prod^k \dfrac{p_k - 1}{p_k}\)。
-
-
欧拉函数可以用线性筛筛出来。
假设当前的数是 \(n\)，遍历到的质数为 \(p\)，那么 \(m = p \times n\) 肯定要被筛掉。根据欧拉筛：
-
若 \(p | n\)，那么 \(p\) 是 \(n\) 的最小质因子，且 \(n\) 中包含 \(m\) 的所有质因子。根据单个欧拉函数的求法可以得到：\(\varphi(m) = \varphi(n) \times p\)。
-
否则，\(p\) 和 \(n\) 互质，根据积性函数的性质，\(\varphi(m) = \varphi(n) \varphi(p)\)。
-
int get_phi(int n) {
phi[1] = 1;
for (int i = 2; i <= n; i ++ ) {
if (!st[i]) p[ ++ cnt] = i, phi[i] = i - 1;
for (int j = 1; j <= cnt and 1ll * i * p[j] <= n; j ++ ) {
st[i * p[j]] = true; if (i % p[j] == 0) {
phi[i * p[j]] = phi[i] * p[j]; break;
} phi[i * p[j]] = phi[i] * phi[p[j]];
}
}
}
- 欧拉函数可以用来降幂。下面就来介绍。
完全剩余系
对于整数集 \(S = \{r_1, r_2 \cdots r_n\}\) 满足：
-
任意不同元素 \(r_i, r_j\)，都有 \(r_i \not \equiv r_j(\bmod \ m)\)。
-
\(\forall a \in \mathbb{Z}\)，\(\exists r \in S, r \equiv a(\bmod \ m)\)。
例如，对于 \(m = 5\)，\(S = \{0, 1, 2, 3, 4\}\) 就是 \(5\) 的一个完全剩余系。通常地，将模 \(m\) 的完全剩余系记做 \(\mathbb{Z_m}\)。
实际应用中，通常用 \(\mathbb{Z_m} = \{0, 1, 2 \cdots m - 1\}\) 来表示，也就是模 \(m\) 的最小非负完全剩余系。
推论 \(1\)：任意 \(m\) 个连续整数构成模 \(m\) 的完全剩余系。
推论 \(2\)：若 \(a \bot m\) 且 \(\mathbb{Z_m}\) 是一个完全剩余系，则 \(S = \{a, 2a \cdots ma\}\) 构成一个完全剩余系。
下面证明推论 \(2\)。
设集合 \(S = \{ra | r \in \mathbb{Z_m}\}\)。对于 \(r_i, r_j \in \mathbb{Z_m}, r_i \ne r_j\)。假设存在同余 \(r_i a \equiv r_j a (\bmod \ m)\)。由于 \(a \bot m\)，因此 \(r_i \equiv r_j(\bmod \ m)\)。根据完全剩余系的互异性，假设不成立。\(S\) 的互异性证明完成。
因为 \(S \subset \mathbb{Z}\)，由定义 \((2)\) 可得，\(\forall a \in S\)，\(\mathbb{Z_m}\) 中有唯一的 \(r\) 满足 \(r \equiv a(\bmod \ m)\)。因此构成 \(S\) 对 \(\mathbb{Z_m}\) 的单射。又因为 \(|S| = |\mathbb{Z_m}|\)，故构成 \(S\) 到 \(\mathbb{Z_m}\) 的双射。
则对于任意整数，都存在 \(\mathbb{Z_m}\) 中的某个数 \(r\) 与之同余，亦存在 \(S\) 中某个数与之同余。定义 \((1)\) 证明完成。因此 \(S\) 是一个完全剩余系。
简化剩余系
在完全剩余系基础上加上了更强的限制。
定义 \(\Phi_m = \{r_1, r_2 \cdots r_s\}\) 为模 \(m\) 的简化剩余系，当且仅当：
-
任意不同元素 \(r_i, r_j \in \Phi_m\)，都有 \(r_i \not \equiv r_j(\bmod \ m)\)。
-
\(\forall a \in \mathbb{Z}\)，\(\exists r \in \Phi_m, r \equiv a(\bmod \ m)\)。
-
\(\forall r \in \Phi_m, r \bot m\)。
其中定义 \((2), (3)\) 可以合并为 \(\forall a \bot m\)，都存在唯一的 \(r \in \Phi_m\) 满足 \(a \equiv r(\bmod \ m)\)。
下面证明简化剩余系的一些推论。
推论 \(1\)：该剩余系对于 \(\bmod \ m\) 的乘法具有封闭性。
证明：\(\forall r_i, r_j \in \Phi_m\)，都有 \(r_i \bot m, r_j \bot m\)。因此有 \(r_i r_j \bot m\)。根据性质 \((2), (3)\)，\(r_i r_j\) 也在 \(\Phi_m\) 中。
根据 \(a_i \bot m \to a_i \bot a_i ^ {-1}\) 可知，\(a_i\) 的乘法逆元也在 \(\Phi_m\) 中。因此证明了关于乘法和除法的封闭性，还证明了逆元的存在。
事实上，该简化剩余系 \(\Phi_m\) 构成关于模 \(m\) 乘法运算的交换群（阿贝尔群）。
推论 \(2\)：\(\varphi(m) = |\Phi_m|\)。
推论 \(3\)：对于 \(m > 2\)，有：
\[\sum _{r \in \Phi_m} r = 0 \]
证明：可能算是感性证明。根据欧几里得算法的流程，\((r, m) = 1\)，则 \((m, m - r) = 1\)，也即 \((m, -r) = 1\)。因此，如果 \(r\) 在 \(\Phi_m\) 中，则 \(-r\) 也在 \(\Phi_m\) 中。由于 \(r\) 与 \(-r\) 模 \(m\) 不相等，因此简化剩余系中的数总是成对出现。相加可以证明。
这也说明，简化剩余系 \(\Phi_m\) 的大小 \(|\Phi_m|\) 一定是偶数（\(m > 2\)）。
推论 \(4\)：若 \(a \bot m\) 且 \(\mathbb{\Phi_m}\) 是一个完全剩余系，则 \(S = \{ra | r \in \Phi_m\}\) 构成一个完全剩余系。
证明方法可以参考完全剩余系性质 \(2\) 的证明。
欧拉定理
定义：若 \(n, a\) 均为正整数，且 \(n\) 与 \(a\) 互质，则有 \(a ^ {\varphi(n)} \equiv 1(\bmod \ n)\)。
证明：对于 \(n\) 的简化剩余系 \(\Phi_n\)，根据简化剩余系的推论 \(4\) 可知，\(S = \{ar | r \in \Phi_n\}\) 也构成模 \(n\) 的简化剩余系。
根据 \(\prod_{r \in \Phi_n} r \equiv \prod_{r \in S} r (\bmod \ n)\)，有 \(a^{|\Phi_n|} = a ^ {\varphi(n)} \equiv 1 (\bmod \ n)\)。证毕。
由此可以得到更弱的定理 Farmet 小定理：\(\forall p \in \mathbb{P}\)，\(a^{p - 1} \equiv 1 (\bmod \ p)\)。
扩展欧拉定理
扩展欧拉定理的证明就不在我能力所及的范围内了。在这就放个结论吧。
这个柿子就比较有用了，可以用来搞降幂之类的事情。
例题
求 \(2 ^ {2 ^ {2 ^ {\cdots ^ {2}}}} \bmod p\) 的值。
设 \(f(p)\) 表示 \(2\) 的幂塔对 \(p\) 取模的值。那么他就等于 \(2 ^ {f(\varphi(p)) + \varphi(p)}\)。由于 \(\varphi\) 函数下降速度极快（\(\log\) 速度），很快 \(\varphi(p)\) 降为 \(1\)。这个东西可以递归求解。
int solve(int p) {
if (p == 1) return 0;
int phi = get_phi(p);
int s = solve(phi);
return qpow(2, s + phi, p);
}
给定一个数列 \(w_1, w_2 \cdots w_n\) 和模数 \(p\), 每次询问一个区间 \([l,r]\)，求 \(w_l ^ {w_{l + 1} ^ {w_{l + 2} ^ {{\cdots}^{w_r}}}} \bmod\ p\) 的值
考虑欧拉降幂。欧拉函数下降速度很快，\(O(\log p)\) 次就能降为 \(1\)。因此可能只需要计算到 \(w_{l + k}\)，后面的就全模 \(1\) 了（当然模 \(1\) 就是 \(0\)）。这个 \(k\) 是 \(O(\log p)\) 级别的。
上面讨论的都是幂次大于 \(\varphi(p)\) 的情况。如果幂次小于 \(\varphi(p)\) 呢？怎么提前判断掉呢？
如果数列的每一项都 \(\ge 2\)，那么可以直接暴力判断，因为 \(O(\log p)\) 个数乘起来就会达到 \(p\)。但是如果存在 \(1\) 呢？这个也好办，直接把 \(r\) 调到 \(l\) 后边的第一个 \(1\) 前面就行，这样保证了 \([l, r]\) 中没有 \(1\)。同时，这个 \(1\) 对答案也没有影响，因为 \(x ^ 1 = x, 1 ^ x = 1\)。
下面是一份可供参考的代码实现：
#include <iostream>
#include <cstring>
#include <cstdio>
#include <map>
#define int long long
using namespace std;
const int N = 100010;
int n, m, p, a[N], suf[N];
map<int, int> bin;
int qpow(int a, int b, int p) {
int s = 1; for (; b; b >>= 1, a = a * a % p)
if (b & 1) s = s * a % p; return s;
}
bool check(int a, int b, int p) {
int s = 1;
for (; b; b >>= 1, a = a * a) {
if (a >= p) return 0;
if (b & 1) {
s = s * a; if (s >= p) return 0;
}
} return 1;
}
int get_phi(int n) {
int s = n;
for (int i = 2; i <= n / i; i ++ ) if (!(n % i)) {
s = s / i * (i - 1); while (!(n % i)) n /= i;
} if (n != 1) s = s / n * (n - 1); return s;
}
int solve(int u, int r, int p) {
if (u == r) return a[u] % p;
if (p == 1) return 0;
int phi = bin[p], s = a[r]; bool flg = 0;
for (int i = r; i > u + 1; i -- ) {
if (!check(a[i - 1], s, phi)) { flg = 1; break; }
s = qpow(a[i - 1], s, phi);
} if (s >= phi) flg = 1; int pw;
if (flg) pw = solve(u + 1, r, phi) + phi;
else pw = s;
return qpow(a[u], pw, p);
}
signed main() {
scanf("%lld%lld", &n, &p);
for (int i = 1; i <= n; i ++ )
scanf("%lld", &a[i]);
scanf("%lld", &m); int t = p; bin[1] = 1;
while (t != 1) bin[t] = get_phi(t), t = bin[t];
suf[n + 1] = n + 1;
for (int i = n; i >= 1; i -- )
if (a[i] == 1) suf[i] = i;
else suf[i] = suf[i + 1];
while (m -- ) {
int l, r; scanf("%lld%lld", &l, &r);
r = min(r, suf[l]); printf("%lld\n", solve(l, r, p));
} return 0;
}
数值算法
高斯消元
高斯消元原理
高斯消元用来解如下形式的方程组：
首先将所有系数写成系数矩阵：
接下来可以进行初等行列变换，将矩阵消成下三角矩阵。类似这样：
然后最后一行就表示 \(a_{n, n} x_n = a_{n, n + 1}\)，可以解出 \(x_n\)。
然后往回带，解出 \(x_{n - 1}\)，以此类推即可。时间复杂度 \(O(n ^ 3)\)。
void gauss() {
rep(i, 1, n) {
rep(j, i, n) if (fabs(a[j][i]) > eps) {
swap(a[j], a[i]); break;
} if (fabs(a[i][i]) <= eps) continue;
rep(j, i + 1, n) {
if (fabs(a[j][i]) <= eps) continue;
db inv = (db)a[j][i] / a[i][i];
rep(k, i, n + 1)
a[j][k] -= inv * a[i][k];
}
}
for (int i = n; i; i -- ) {
f[i] = a[i][n + 1] / a[i][i];
for (int j = i - 1; j; j -- )
a[j][n + 1] -= a[j][i] * f[i];
}
}
高斯消元应用
- 解线性方程组
这个不用我说了吧。。。
- 在 \(\text{dp}\) 中用于消元
这个用处非常大。举个栗子：P3232 [HNOI2013] 游走
题意：给定 \(n\) 点 \(m\) 边无向简单图。要求给每条边重新编号 \(1 \sim m\)，使得每条边编号不同且从 \(1\) 到 \(n\) 经过路径的权值和期望尽可能小。
\(n \le 500, m \le 125000\)。
发现边数很多，所以从点数入手。设 \(f_i\) 表示第 \(i\) 个点被经过的期望次数，那么有：
当然，\(n\) 号点被我们排除在外，因为到了 \(n\) 就停止了。
然后发现，上面的柿子形成了一个 \(n - 1\) 元方程。用高斯消元解方程就可以得到 \(f_u\)。
然后可以得到每条边被经过的期望次数：\(g_{(u, v)} = \dfrac{f_u}{deg_u} + \dfrac{f_v}{deg_v}\)。根据边被经过的期望次数贪心赋权即可。
其他用高斯消元求解 \(dp\) 的例题：P4321 随机漫游
- 矩阵求逆
矩阵 \(A\) 的逆矩阵定义为 \(A^{-1}\)，满足 \(A^{-1} \times A = I\) 且 \(A ^ {-1} \times A = I\)。其中 \(I\) 表示单位矩阵。
求法：将原矩阵 \(A\) 右面拼上一个单位矩阵 \(I\)。然后对左边一半也就是 \(A\) 做初等行列变换消成单位矩阵，同时对右边做左边同样的操作（左边行加右边也加，左边同乘右边也同乘）。最后得到的右半边就是 \(A ^ {-1}\)。
证明真的不会/kk
int gauss() {
rep(i, 1, n) {
rep(j, i, n)
if (a[j][i] != 0) {
swap(a[i], a[j]); break;
}
if (a[i][i] == 0) return 0;
rep(j, i + 1, n) {
if (a[j][i] == 0) continue;
int inv = a[j][i] * qpow(a[i][i]) % mod;
rep(k, i, 2 * n) a[j][k] -= inv * a[i][k] % mod,
a[j][k] = (a[j][k] % mod + mod) % mod;
}
}
rep(i, 1, n) {
int inv = qpow(a[i][i]);
rep(j, 1, 2 * n) a[i][j] = a[i][j] * inv % mod;
}
dep(i, n, 1) {
rep(j, 1, i - 1) {
int inv = a[j][i];
rep(k, 1, 2 * n) a[j][k] -= a[i][k] * inv % mod,
a[j][k] = (a[j][k] % mod + mod) % mod;
}
} return 1;
}
signed main() {
read(n); int B = (10 * n + 5) * sizeof(LL);
rep(i, 0, n + 1) a[i] = (LL*)malloc(B);
rep(i, 1, n) rep(j, 1, n) read(a[i][j]);
rep(i, 1, n) a[i][i + n] = 1; int s = gauss();
if (!s) return puts("No Solution"), 0;
for (int i = 1; i <= n; i ++ , pc('\n'))
rep(j, 1, n) write(' ', a[i][j + n]);
return 0;
}
卷积及反演
某些定义
一些常见的积性函数。
-
莫比乌斯函数 \(\mu(n)\)。
-
欧拉函数 \(\varphi(n)\)：\(1 \sim n\) 中与 \(n\) 互质的数的个数。
-
约数个数 \(d(n)\)：\(n\) 的约数个数。
-
约数和 \(\sigma\)：\(\sum \limits_{d | n}^{} d\)。
-
元函数 \(\epsilon(n)\)。即 \([n = 1]\)。
-
单位函数 \(\text{id}(n)\)。即为 \(n\)。
-
恒等函数 \(\text{I}(n)\)。该函数恒为 \(1\)。有时也写作 \(1\)。
狄利克雷卷积
定义两个数论函数的狄利克雷卷积为 \((f * g)(n) = \sum \limits_{d | n} f(d) g(\dfrac{n}{d})\)，读作 \(f\) 卷 \(g\)。
其中后面括号里的 \(n\) 代表卷积范围。
卷积有下面这些良好的性质：
-
交换律：\(f * g = g * f\)。
-
结合律：\((f * g) * h = f * (g * h)\)。
上面的性质可以根据卷积定义证明。这里略过。
常见数论函数的狄利克雷卷积
- \(d = 1 * 1\)
证明：\(1 * 1 = \sum \limits_{d | n}^{} 1 \times 1 = d(n)\)。
- \(\epsilon = \mu * 1\)
上文提到过，\(\sum \limits_{d | n} \mu = [n = 1] = \epsilon(n)\)。
- \(\text{id} = \varphi * 1\)
利用欧拉函数性质证明。
\(\text{(1)}\) \(\varphi(1) = 1\)
\(\text{(2)}\) \(\varphi(p) = p - 1\)
\(\text{(3)}\) \(\varphi(p ^ 2) = p \times \varphi(p) = p ^ 2 - p\)
\(\text{(4)}\) 根据性质 \((3)\)， 推出 \(\varphi(p ^ k) = \varphi(p) \times p^{k - 1} = p ^ k - p ^{k - 1}\)
\((5)\) \(\sum \limits_{i = 0}^{c} \varphi(p ^ i) = 1 + \sum \limits_{i = 1}^{c} \varphi(p ^ i) = 1 + \sum \limits_{i = 1}^{c} p ^ i - p^{i - 1} = p ^ c\)
\((6)\) 若 \(n = \sum \limits_{i = 1}^{k} p_i ^ {c_i}\)，则利用 \((5)\) 和积性函数的性质即可推出。
- \(\varphi = \mu * \text{id}\)
证明：由于 \(\text{id} = \varphi * 1\)，根据卷积的性质，可以在等式两边同时卷上 \(\mu\)，得到 \(\text{id} * \mu = \varphi * 1 * \mu\)。根据 \(\mu * 1 = \epsilon\) 得 \(\text{id} * \mu = \varphi * \epsilon = \varphi\)。证毕。
- \(\sigma = \text{id} * 1\)
证明：\(\sigma(n) = \sum \limits_{d | n} d = \sum \limits_{d | n} \text{id}(d) \times I(\dfrac{n}{d}) = \text{id} * 1(n)\)。
莫比乌斯反演
莫比乌斯反演的形式如下：
如果存在 \(F(n) = \sum \limits_{d | n} f(d)\)，那么有 \(f(n) = \sum \limits_{d | n} F(d) \mu(\dfrac{n}{d})\)。
该结论可以利用狄利克雷卷积来证明。
证明：
\(F(n) = \sum \limits_{d | n} f(d)\) 写成卷积的形式就是 \(F = f * 1(n)\)。那么对两边同时卷上 \(\mu\)，可得 \(F * \mu(n) = f * 1 * \mu(n)\)。由于 \(1 * \mu(n) = \epsilon\)，所以原式可化为 \(F * \mu(n) = f * \epsilon(n) = f\)，即 \(f(n) = \sum \limits_{d | n} F(d) \mu(\dfrac{n}{d})\)。证毕。
某些例题：
下面求和的上界省略了下取整符号。
\(\text{P3455 [POI2007]ZAP-Queries}\)
求 \(\sum \limits_{i = 1}^{n} \sum \limits_{j = 1}^{m} [(i, j) = k]\)。
大力莫反。
前面的 \(\mu\) 可以线筛，后面的可以整除分块套上 \(\mu\) 前缀和。
\(\text{P2522 [HAOI2011]Problem b}\)
求 \(\sum \limits_{i = a}^{b} \sum \limits_{j = c}^{d} [(i, j) = k]\)。
上一道题的强化版。将上一道题写成函数 \(\operatorname{calc(n, m, k)}\)，表示求 求 \(\sum \limits_{i = 1}^{n} \sum \limits_{j = 1}^{m} [(i, j) = k]\) 的值。然后利用类似二维前缀和的方式，计算出答案即为 \(\operatorname{calc(b, d, k)} - \operatorname{calc(a - 1, d, k)} - \operatorname{calc(c - 1, b, k)} + \operatorname{calc(a - 1, c - 1, k)}\)
首先考虑计算 \(\sum \limits_{i = 1}^n \sum \limits_{j = 1}^n (i, j)\)。
首先枚举 \((i, j)\)，得到 \(\sum \limits_{d = 1}^{n} d \sum \limits_{i = 1}^{n} \sum \limits_{j = 1}^{n} [(i, j) = d]\)
继续化简：
\(\varphi\) 可以前缀和，然后整除分块就好了。复杂度 \(O(n + \sqrt n)\)，瓶颈在前缀和。
原题要求的就是刚才求的减去 \(\sum i\) 之后在除以 \(2\) 。这里根据最大公约数的交换律或者对称性易得。
另外，这个题也可以不必卷到 \(\varphi\)。只要卷到 \(= \sum \limits_{d = 1}^{n} d \sum \limits_{p = 1}^{\frac{n}{d}} \mu(p) \left \lfloor \dfrac{n}{pd} \right \rfloor \left \lfloor \dfrac{n}{pd} \right \rfloor\) 就可以套两层整除分块了。这样的复杂度是 \(O(n + n) = O(n)\)，也很优秀。
一天后返回来在看一眼原来推得式子，会发现确实推复杂了。正难则反，直接用 \(\varphi * 1 = id\) 来推。
可以发现结果是一样的。
设质数集为 \(\mathbb{P}\)，求：
又到了愉快的推式子时间：这里设 \(n \le m\)，
然后发现两个下取整可以直接整除分块，瓶颈就在计算 \(\sum \limits_{d | k, d \in \mathbb{P}} \mu(\dfrac{k}{d})\) 上。这个玩意可以筛出质数后预处理。
预处理复杂度 \(O(n + n \log \log n)\)，计算复杂度 \(O(T \sqrt n)\)。总复杂度 \(O(n + n \log \log n + T \sqrt n)\)。
看了一下题解，预处理也可以线性筛。不过不想看了，反正能过就行。
void init() {
mu[1] = 1;
for (int i = 2; i <= N - 5; i ++ ) {
if (!is_prime[i]) p[ ++ cnt] = i, mu[i] = -1;
for (int j = 1; j <= cnt and i * p[j] <= N - 5; j ++ ) {
is_prime[i * p[j]] = true;
if (i % p[j] == 0) break;
mu[i * p[j]] = - mu[i];
}
}
for (int i = 1; i <= cnt; i ++ )
for (int j = 1; p[i] * j <= N - 5; j ++ )
f[p[i] * j] += mu[j];
for (int i = 1; i <= N - 5; i ++ )
s[i] = s[i - 1] + f[i];
}
void substack() {
scanf("%lld%lld", &n, &m);
if (n > m) swap(n, m);
int ans = 0;
for (int l = 1, r; l <= n; l = r + 1) {
r = min(n / (n / l), m / (m / l));
ans += (n / l) * (m / l) * (s[r] - s[l - 1]);
}
printf("%lld\n", ans);
}
\(\text{P3327 [SDOI2015]约数个数和}\)
设 \(d(x)\) 为 \(x\) 的约数个数，给定 \(n,m\)，求
有结论：\(d(ij) = \sum \limits_{x | i}^{} \sum \limits_{y | j}^{} [(x, y) = 1]\)
于是可以愉快地推柿子了。
不妨设 \(f(n) = \sum \limits_{i = 1}^{n} \left \lfloor \dfrac{n}{i} \right \rfloor\)，可以发现这个玩意就等于 \(\sum \limits_{i = 1}^{n}d(i)\)。而这个东西可以筛 \(\mu\) 的时候预处理出来。
于是柿子变成 \(\sum \limits_{d = 1}^{\min(n, m)} \mu(d) f(\dfrac{n}{d}) f(\dfrac{m}{d})\)。整出分块即可。总复杂度 \(O(T \sqrt n)\)。预处理可以用线性筛，但是懒得写了，直接莽了个 \(O(n \log n)\) 暴力上去。
void init(int n) {
mu[1] = 1;
for (int i = 2; i <= n; i ++ ) {
if (!is_prime[i]) p[ ++ cnt] = i, mu[i] = -1;
for (int j = 1; j <= cnt and i * p[j] <= n; j ++ ) {
is_prime[i * p[j]] = true;
if (i % p[j] == 0) break;
mu[i * p[j]] = -mu[i];
}
}
for (int i = 1; i <= n; i ++ )
mu_s[i] = mu_s[i - 1] + mu[i];
for (int i = 1; i <= n; i ++ )
for (int j = i; j <= n; j += i)
s[j] ++ ;
for (int i = 1; i <= n; i ++ )
s[i] += s[i - 1];
}
void substack() {
scanf("%lld%lld", &n, &m);
int ans = 0;
for (int l = 1, r; l <= min(n, m); l = r + 1) {
r = min(n / (n / l), m / (m / l));
ans += s[n / l] * s[m / l] * (mu_s[r] - mu_s[l - 1]);
}
printf("%lld\n", ans);
}
组合数学
定义
\(C_{n}^{m}\)，也记做 \(\dbinom{n}{m}\)，表示从 \(n\) 个元素中选择 \(m\) 个且不考虑顺序的方案数。有公式：
这个公式是怎么得到的呢？首先，先假设考虑顺序。那么选择第一个数的方案就有 \(n\) 种。然后再选一个，就要从剩下的 \(n - 1\) 个里面选，以此类推。总方案数就是 \(\dfrac{n!}{(n - m)!}\)。
那么如果不考虑顺序，那么需要再除以排列数 \(m!\)。
对于组合数的讨论，一般规定 \(0! = 1\)，\(n \ge m\)。
求法
三种方法求组合数：
- \(n, m \le 5000\)
可以用杨辉三角来求解。有组合恒等式：
再根据 \(\dbinom{n}{0} = 1\)，\(O(n ^ 2)\) 递推求解即可。
- \(n, m \le 10000000\)，答案对 \(p\) 取模（\(p\) 为质数）
根据上面的公式：\(\dbinom{n}{m} = \dfrac{n!}{m! \times (n - m)!}\)，可以预处理出阶乘和阶乘逆元，然后 \(O(1)\) 计算。时间复杂度 \(O(n) \sim O(1)\)
- \(n, m \le 10 ^ {18}\)，答案对 \(p\) 取模（\(p\) 为质数且 \(p \le 10 ^ 5\)）
引理：\(\text{Lucas}\) 定理
对于质数 \(p\)，有 \(\dbinom{n}{m} \equiv \dbinom{\lfloor \frac{n}{p} \rfloor}{\lfloor \frac{m}{p} \rfloor} \times \dbinom{n \bmod \ p}{m \bmod \ p}(\bmod \ p)\) 恒成立。
组合恒等式及证明
- \(\dbinom{n}{k} = \dbinom{n}{n - k}\)
这个组合意义理解一下好了。从 \(n\) 个里面选出 \(k\) 个的方案数，也就等于从 \(n\) 个里面不选 \(n - k\) 个数的方案数。
多项式与生成函数
多项式
开头先扔板子：多项式板子们
定义
多项式（polynomial）是形如 \(P(x) = \sum \limits_{i = 0}^{n} a_i x ^ i\) 的代数表达式。其中 \(x\) 是一个不定元。
\(\partial(P(x))\) 称为这个多项式的次数。
多项式的基本运算
- 多项式的加减法
- 多项式的乘法
- 多项式除法
这里讨论多项式的带余除法。
可以证明，一定存在唯一的 \(q(x), r(x)\) 满足 \(A(x) = q(x) B(x) + r(x)\)，且 \(\partial(r(x)) < \partial(B(x))\)。
\(q(x)\) 称为 \(B(x)\) 除 \(A(x)\) 的商式，\(r(x)\) 称为 \(B(x)\) 除 \(A(x)\) 的余式。记作：
特别的，若 \(r(x) = 0\)，则称 \(B(x)\) 整除 \(A(x)\)，\(A(x)\) 是 \(B(x)\) 的一个倍式，\(B(x)\) 是 \(A(x)\) 的一个因式。记作 \(B(x) | A(x)\)。
有关多项式的引理
-
对于 \(n + 1\) 个点可以唯一确定一个 \(n\) 次多项式。
-
如果 \(f(x), g(x)\) 都是不超过 \(n\) 次的多项式，且它对于 \(n +1\) 个不同的数 \(\alpha_1, \alpha_2 \cdots \alpha_n\) 有相同的值，即 \(\forall i \in [1, n + 1], i \in \mathbb{Z}, f(\alpha_i) = g(\alpha_i)\)。则 \(f(x) = g(x)\)。
多项式的点值表示
如果选取 \(n + 1\) 个不同的数 \(x_0, x_1, \cdots x_n\) 对多项式进行求值，得到 \(A(x_0), A(x_1) \cdots A(x_n)\)，那么就称 \(\{(x_i, A(x_i)) \ | \ 0 \le i \le n, i \in \mathbb{Z} \}\) 为 \(A(x)\) 的点值表示。
快速傅里叶变换（FFT）
快速傅里叶变换是借助单位根进行求值和插值，从而快速进行多项式乘法的算法。
单位根
将复平面上的单位圆均分成 \(n\) 份，从 \(x\) 轴数，第 \(i\) 条线与单位圆的交点称为 \(i\) 次单位根，记作 \(\omega_{n}^{i}\)。
根据定义，可以得到：\(\omega_{n}^{1} = i \sin \alpha +\cos \alpha, \alpha = \frac{2 \pi}{n}\)。
引理：欧拉公式
\(\forall \theta \in R\)，\(e ^ {i\theta} = i\sin \theta + \cos \theta\)。
根据欧拉公式，可以得到：\(\omega_{n}^{1} = e ^ {\frac{2 \pi i}{n}}\)。
由此那么可以得到下面的性质：
-
\(\omega_{n}^{i} \times \omega_{n}^{j} = \omega_{n}^{i + j}\)
-
\(\omega_{n}^{i + \frac{n}{2}} = - \omega_{n}^{i}\)
-
\(\omega_{n}^{i + n} = \omega_{n}^{i}\)
另外一种理解方式是通过棣莫弗公式。
引理：棣莫弗公式
\(\forall \theta \in R\)，\((\cos \theta + i \sin \theta) ^ n = \cos (n\theta) + i \sin (n\theta)\)
考虑两个复平面上的向量
计算两个向量相乘的结果，可得：
当 \(\theta_1 = \theta_2, \rho_1 = \rho_2\) 时便是大名鼎鼎的棣莫弗公式。
因此可以得到，单位圆上的两个复数相乘，模长不变（也就是还在单位圆上），幅角相加。然后可以由此理解上面的三个单位根性质。
离散傅里叶变换（DFT）
离散傅里叶变换，是将 \(\omega_{n}^{k}, 0 \le k < n\) 代入 \(f(x)\) 和 \(g(x)\) 中求值的过程。
对于朴素的方法，每次代入一个单位根，然后用 \(O(n)\) 的复杂度计算函数值。时间复杂度 \(O(n ^ 2)\)。
离散傅里叶变换利用了单位根的性质巧妙优化了这个过程。离散傅里叶变换过程如下：
首先将 \(f(x)\) 根据次数的奇偶性拆成两部分，分别分为：
设
则 \(f(x) = e'(x ^ 2) + x o'(x ^ 2)\)。
将 \(\omega_{n}^{k}\) 代入得到：
然后你发现，\(f(\omega_{n}^{k})\) 和 \(f(\omega_{n}^{k + \frac{n}{2}})\) 仅仅差了一个符号！！！
所以只需要求出 \(e'(x)\) 和 \(o'(x)\) 对 \(\omega^{k}_{n}\)（\(0 \le k \le \frac{n}{2}\)）上的取值，就可以推出 \(f(x)\) 在两倍点数上的取值。
每次问题规模缩小一半，因此时间复杂度 \(O(n \log n)\)。
离散傅里叶逆变换（IDFT）
假设对于两个多项式都得到了 \(t = n + m - 1\) 个点值，设为 \(\{(x_i, A(x_i)) \ | \ 0 \le i < t, i \in \mathbb{Z} \}, \{(x_i, B(x_i)) \ | \ 0 \le i < t, i \in \mathbb{Z} \}\)。
那么可以知道，多项式 \(C(x) = A(x) \times B(x)\) 的点值表示一定为：
现在，只需要将这 \(t\) 个点插值回去，就可以得到 \(A(x)B(x)\) 了。
先设这 \(t\) 个点值分别是：\(\{(x_i, v_i) \ | \ 0 \le i < t, i \in \mathbb{Z} \}\)，设最后的多项式为 \(C(x) = \sum \limits_{i = 0}^{n + m - 2} c_i x^i\)，这里直接给出结论：
由此可见，IDFT 和 DFT 仅仅有一个负号的区别。只要将所有的单位根从 \(\omega_{n}^{k}\) 变成 $ \omega_{n}^{-k}$ 即可。
void FFT(cp a[], int n, int op) {
if (n == 1) return;
cp a1[n], a2[n];
rop(i, 0, n >> 1) a1[i] = a[i << 1], a2[i] = a[(i << 1) + 1];
FFT(a1, n >> 1, op), FFT(a2, n >> 1, op);
cp Wn = {cos(2 * pi / n), op * sin(2 * pi / n)};
cp Wk = {1, 0};
rop(i, 0, n >> 1) {
a[i] = a1[i] + Wk * a2[i];
a[i + (n >> 1)] = a1[i] - Wk * a2[i];
Wk = Wk * Wn;
}
}
void FFT(cp a[], cp b[], int n, int m) {
m = n + m; n = 1;
while (n <= m) n <<= 1;
FFT(a, n, 1); FFT(b, n, 1);
rop(i, 0, n) a[i] = a[i] * b[i];
FFT(a, n, -1);
rep(i, 0, m) a[i].x = a[i].x / n;
}
FFT 优化
- 三次变两次优化
原本的朴素 FFT，将 \(\{a\}, \{b\}\) 两个序列分别求值，乘起来再 IDFT 插值一下，一共跑了三次 FFT。这是不好的。
三次变两次优化是这样的：将原序列合并成一个复数：\(\{a_i + b_i \times i\}\)。做一遍 DFT 把求出的每个函数值平方。因为 \((a + bi) ^ 2 = (a ^ 2 - b ^ 2) + (2abi)\)。因此把虚部取出来以后除以 \(2\) 就是答案。
void FFT(cp a[], int n, int op) {
if (n == 1) return;
cp a1[n], a2[n];
rop(i, 0, n >> 1) a1[i] = a[i << 1], a2[i] = a[(i << 1) + 1];
FFT(a1, n >> 1, op), FFT(a2, n >> 1, op);
cp Wn = {cos(2 * pi / n), op * sin(2 * pi / n)};
cp Wk = {1, 0};
rop(i, 0, n >> 1) {
a[i] = a1[i] + a2[i] * Wk;
a[i + (n >> 1)] = a1[i] - a2[i] * Wk;
Wk = Wk * Wn;
}
}
int main() {
read(n, m);
rep(i, 0, n) scanf("%lf", &a[i].x);
rep(i, 0, m) scanf("%lf", &a[i].y);
m = n + m; n = 1;
while (n <= m) n <<= 1;
FFT(a, n, 1);
rop(i, 0, n) a[i] = a[i] * a[i];
FFT(a, n, -1);
rep(i, 0, m) printf("%d ", (int)(a[i].y / 2 / n + 0.5));
}
- 蝴蝶变换优化
后面再补吧。其实本人感觉这个优化不是那么必要，因为三次变两次实在太快了。
FFT 例题
可以设 \(x = 10\)，把 \(a\) 写成 \(A(x) = \sum \limits_{i = 0}^{n} a_i x^i\) 的形式（\(n = \log_{10} a\)）。同理可以把 \(b\) 转化为多项式 \(B(x)\)。
这样求两个数相乘就是求 \(A(x) \times B(x)\) 啊。
所以直接 \(O(n \log n)\) 做完了。
给出 \(n\) 个数 \(q_1,q_2, \dots q_n\)，定义
对 \(1 \leq i \leq n\)，求 \(E_i\) 的值。
首先发现这个除以 \(q_i\) 就是没用。所以可以化简成：
先看前面这个式子。答案就是：
设 \(f(x) = \sum q_i x ^ i, g(x) = \dfrac{1}{i ^ 2} x ^ i\)。可以发现，\(E_j' = (f \times g)[j]\)
再看后面这一块的式子。我们把 \(f(x)\) 的系数翻转，变成 \(f'(x) = \sum q_{n - j + 1} x ^ j\)。那么可以发现 \(E_{j}'' = (f' \times g)[n - j + 1]\)。
跑两次 FFT 就完事了。
首先发现加减相对于两个手环是对称的。因此可以把对一个手环的减法转化成对另一个手环的加法。这样可以假设全是在第一个手环上执行的加减操作。
第一个手环执行了加 \(c\) 的操作，且旋转过之后的序列为 \([x_1, x_2 \cdots x_n]\)，第二个手环为 \([y_1, y_2 \cdots y_n]\)。计算差异值并化简，可以得到差异值是：
可以发现，这个序列只有最后一项是不定的。
因此将 \(y\) 序列翻转后再复制一倍，与 \(x\) 卷积，答案就是卷积后序列的 \(n + 1 \sim 2n\) 项系数的 \(\max\)。
直接暴力枚举 \(c\)，加上前面依托就行了。
快速数论变换（NTT）
快速数论变换就是基于原根的快速傅里叶变换。
首先考虑快速傅里叶变换用到了单位根的什么性质。
-
\(\omega_{n}^{k}, 0 \le k < n\) 互不相同。
-
\(\omega_{n}^{k} = \omega_{n}^{k + \frac{n}{2}}\)。
-
\(\omega_{n}^{k} = \omega_{2n}^{2k}\)。
数论中，原根恰好满足这些性质。
对于一个素数的原根 \(g\)，设 \(g_n = g ^ {\frac{p - 1}{n}}\)。那么：
我们发现它满足 \(\omega_{n}^{k}\) 的全部性质！
因此，只需要用 \(g_{n}^k = g_{}^{\frac{p - 1}{n} k}\) 带替全部的 \(\omega_{n}^{k}\) 就可以了。
tips：对于一个质数，只有当它可以表示成 \(p = 2 ^ \alpha + 1\)，且需要满足多项式的项数 \(< \alpha\) 时才能使用 NTT。\(p\) 后面有个加一，是因为 \(g_n\) 指数的分子上出现了 \(-1\)；\(p - 1\) 需要时二的整数次幂，是因为每次都要除以 \(2\)。
bonus：常用质数及原根
\(p = 998244353 = 119 \times 2 ^ {23} + 1, g = 3\)
\(p = 1004535809 = 479 \times 2 ^ {21} + 1, g = 3\)
void NTT(int *a, int n, int op) {
if (n == 1) return;
int a1[n], a2[n];
rop(i, 0, n >> 1) a1[i] = a[i << 1], a2[i] = a[(i << 1) + 1];
NTT(a1, n >> 1, op), NTT(a2, n >> 1, op);
int gn = qpow((op == 1 ? g : invg), (mod - 1) / n), gk = 1;
rop(i, 0, n >> 1) {
a[i] = (a1[i] + 1ll * gk * a2[i]) % mod;
a[i + (n >> 1)] = (a1[i] - 1ll * gk * a2[i] % mod + mod) % mod;
gk = 1ll * gk * gn % mod;
}
}
NTT 优化：蝴蝶变换
盗大佬一张图
这是进行 NTT 的过程中数组下标的变化。
这样看似乎毫无规律。但是把他们写成二进制：
变换前：\(000 ~ 001 ~ 010 ~ 011 ~ 100 ~ 101 ~ 110 ~ 111\)
变换后：\(000 ~ 100 ~ 010 ~ 110 ~ 001 ~ 101 ~ 011 ~ 111\)
可以发现，就是对每个下标进行了二进制翻转。
因此可以先预处理出每个下标在递归底层对应的新下标。然后从底层往顶层迭代合并。
预处理每个下标的二进制翻转：
rop(i, 0, n) rev[i] = rev[i >> 1] >> 1 | (i & 1) << bit;
优化后的 NTT：
void NTT(int *a, int n, int op) {
rop(i, 0, n) if (i < rev[i]) swap(a[i], a[rev[i]]);
for (int mid = 1; (mid << 1) <= n; mid <<= 1) {
int gn = qpow((op == 1 ? g : invg), (mod - 1) / (mid << 1));
for (int i = 0, gk = 1; i < n; i += (mid << 1), gk = 1)
for (int j = 0; j < mid; j ++ , gk = 1ll * gk * gn % mod) {
int x = a[i + j], y = 1ll * a[i + j + mid] * gk % mod;
a[i + j] = Mod(x + y), a[i + j + mid] = Mod(x - y);
}
}
}
当然了，FFT 也可以用蝴蝶变换来优化。实践证明，速度变快了至少二分之一。
FFT 的迭代实现
void FFT(cp *a, int n, int op) {
rop(i, 0, n) if (i < rev[i]) swap(a[i], a[rev[i]]);
for (int mid = 1; (mid << 1) <= n; mid <<= 1) {
cp Wn = {cos(pi / mid), op * sin(pi / mid)};
for (int i = 0; i < n; i += (mid << 1)) {
cp Wk = {1, 0};
for (int j = 0; j < mid; j ++ , Wk = Wk * Wn) {
cp x = a[i + j], y = Wk * a[i + j + mid];
a[i + j] = x + y, a[i + j + mid] = x - y;
}
}
}
}
任意模数多项式乘法（MTT）
计算 \(f \times g(\bmod ~ p)\) 的结果（\(p\) 不一定能够表示成 \(2 ^ \alpha + 1\) 的形式）。
这个东西有两种做法，但是我只学会了三模 NTT。
首先，卷积之后每个系数最多达到 \(\max \{V\} ^ 2 \times n\) 的大小。拿模板题举例，这个东西就是 \(10 ^ {23}\)。因此只需要找三个模数 \(p_1, p_2, p_3\)，满足 \(p_1p_2p_3 > \max \{V\} ^ 2 \times n\)，然后用他们分别 NTT，最后再 CRT / exCRT 合并即可。
int CRT(int a, int b, int c, int p) {
int k = 1ll * Mod(b - a, p2) * inv1 % p2;
LL x = 1ll * k * p1 + a;
k = 1ll * Mod((c - x) % p3, p3) * inv2 % p3;
x = (x + 1ll * k * p1 % p * p2 % p) % p;
return x;
}
void MTT(int *a, int n, int *b, int m, int p) {
int B = ((n + m) << 2) + 1;
rev = new int [B]();
int *a1 = new int [B](), *b1 = new int [B]();
int *a2 = new int [B](), *b2 = new int [B]();
int *a3 = new int [B](), *b3 = new int [B]();
rop(i, 0, B)
a1[i] = a2[i] = a3[i] = a[i], b1[i] = b2[i] = b3[i] = b[i];
NTT(a1, n, b1, m, p1); NTT(a2, n, b2, m, p2); NTT(a3, n, b3, m, p3);
inv1 = inv(p1, p2); inv2 = inv(1ll * p1 * p2 % p3, p3);
rep(i, 0, n + m) a[i] = CRT(a1[i], a2[i], a3[i], p);
}
这里选择的模数为：\(p_1 = 998244353, p_2 = 469762049, p_3 = 1004535809\)。他们的原根都为 \(g = 3\)。
多项式求逆
求多项式 \(f(x)\) 的逆元 \(f^{-1}(x)\)。\(f(x)\) 的逆元定义为满足 \(f(x) g(x) = 1(\bmod \ x ^ n)\) 的多项式 \(g(x)\)。
使用倍增法即可求出多项式的逆元。
首先假设已经求出了 \(f(x) g'(x) \equiv 1(\bmod \ x ^ {\lceil \frac{n}{2} \rceil})\)。再假设 \(f(x) \bmod \ x ^ n\) 意义下逆元为 \(g(x)\)。那么有：
两边同时乘以 \(f(x)\)，可以得到：
倍增求即可。
void Inv(int *f, int *g, int n) {
if (n == 1) {
g[0] = inv(f[0]); return;
} Inv(f, g, (n + 1) >> 1);
int m = 1, bit = 0;
while (m < (n << 1)) m <<= 1, bit ++ ; bit -- ;
rop(i, 0, n) tmp[i] = f[i];
rop(i, n, m) tmp[i] = 0;
rev = new int [m + 5]();
rop(i, 1, m) rev[i] = (rev[i >> 1] >> 1) | (i & 1) << bit;
NTT(tmp, m, 1); NTT(g, m, 1);
rop(i, 0, m) g[i] = (2ll - 1ll * g[i] * tmp[i] % p + p) % p * g[i] % p;
NTT(g, m, -1); int invn = inv(m);
rop(i, 0, m) g[i] = 1ll * g[i] * invn % p;
rop(i, n, m) g[i] = 0;
free(rev); rev = NULL;
}
分治 FFT
给定序列 \(g_{1\dots n - 1}\)，求序列 \(f_{0\dots n - 1}\)。
其中 \(f_i=\sum_{j=1}^if_{i-j}g_j\)，边界为 \(f_0=1\)。
答案对 \(998244353\) 取模。
其实这是个多项式求逆板子
首先考虑生成函数 \(F(x) = \sum _{i = 0}^{+ \infty} f_i x ^ i, G(x) = \sum _{i = 0}^{ + \infty}g_i x ^ i\)。然后可以发现：
因此 \(F(x)(G(x) - 1) = -f_0\)，也就是：
所以直接设 \(g_0 = 0\)，然后把 \(1 - g\) 求逆就行了。
read(n);
rop(i, 1, n) read(g[i]);
rop(i, 1, n) g[i] = Poly::p - g[i];
(g[0] += 1) %= Poly::p; Poly::Inv(g, n);
rop(i, 0, n) write(' ', g[i]); return 0;
多项式对数函数（Polyln）
给定 \(f(x)\)，求多项式 \(g(x)\) 使得 \(g(x) \equiv \ln(f(x)) (\bmod \ x ^ n)\)
前置知识：简单的求导和积分，以及基本的多项式模板。
首先设 \(h(x) = \ln(x)\)，那么
然后对同余方程两边同时求导，得到
根据复合函数求导公式 \(f'(g(x)) = f'(g(x))g'(x)\) 可得，
然后又有 \(\ln '(x) = \dfrac{1}{x}\)，因此
计算 \(f'(x)\) 和 \(f^{-1}(x)\) 作为 \(a, b\)。计算 \(a \times b (\bmod \ 998244353)\) 得到 \(g'(x)\) ，然后求 \(g'(x)\) 的积分就好了。
积分公式：\(\int x ^ a \mathrm{dx} = \dfrac{1}{a + 1} x ^ {a + 1}\)。
void der(int *f, int n) { rep(i, 1, n) f[i - 1] = 1ll * i * f[i] % p; f[n] = 0; }
void Int(int *f, int n) {dep(i, n, 1) f[i] = 1ll * inv(i) * f[i - 1] % p; f[0] = 0; }
void Ln(int *f, int n) {
int B = (n << 2) + 5; int *_f = new int[B]();
rep(i, 0, n) _f[i] = f[i];
der(_f, n), Inv(f, n);
NTT(f, n, _f, n); Int(f, n);
free(_f); _f = NULL;
}
多项式指数函数（PolyExp）
给定多项式 \(f(x)\)，求 \(g(x)\) 满足 \(g(x) \equiv e ^ {f(x)} (\bmod \ x ^ n)\)。
前置知识：牛顿迭代。
牛顿迭代是用来求函数零点的有力工具。
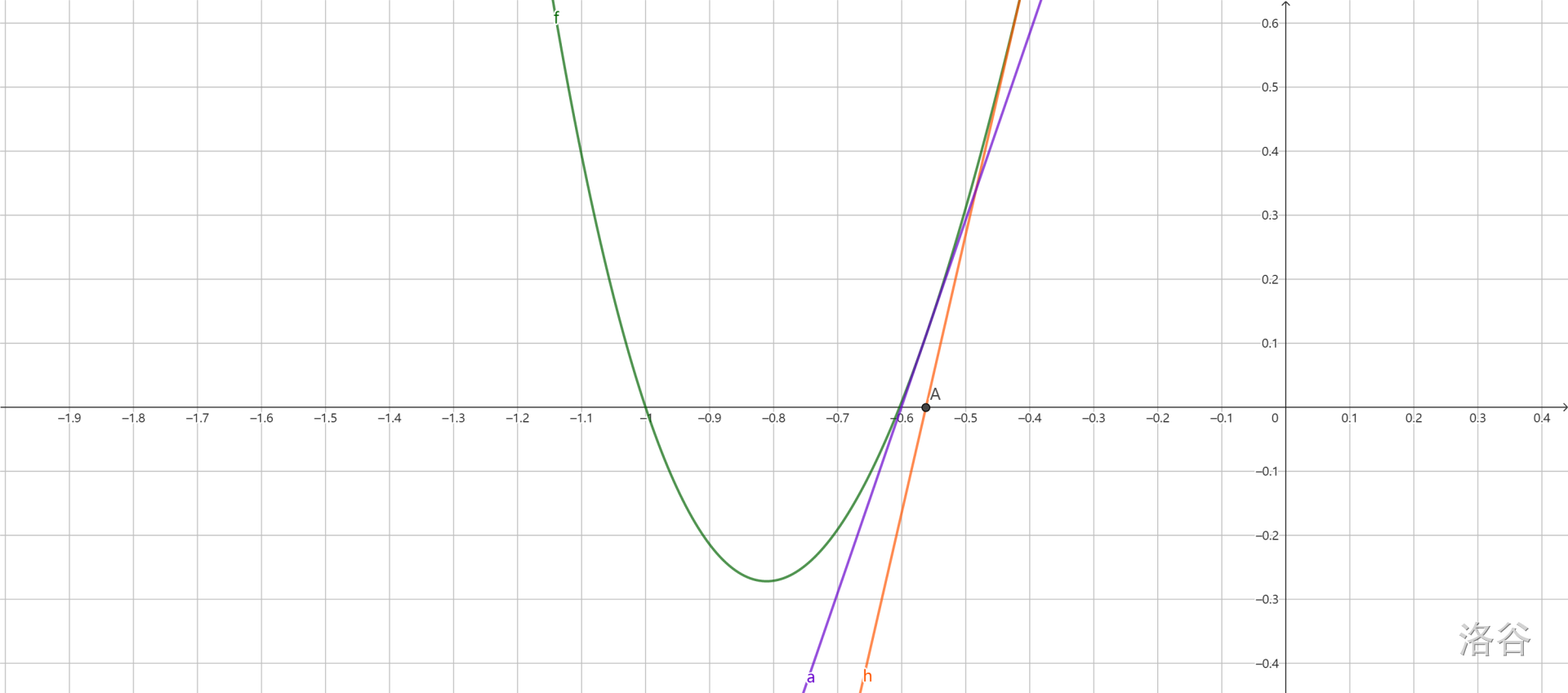
例如，下面这个图是使用牛顿迭代法求 \(f(x)=x^4+3 x^2+7 x+3\) 零点的过程。
首先，随便选择一个点 \((x_0, f(x_0))\)，过这个点做 \(f(x)\) 的切线。切线方程是 \(y = f'(x_0)(x - x_0) + f(x_0)\)。它与 \(x\) 轴交于一点 \(A(-0.56243, 0)\)。
接下来，再令 \(x_1 = -0.56243\)，过点 \((x_1, f(x_1))\) 再做 \(f(x)\) 的切线，与 \(x\) 轴交于点 \(B(-0.60088, 0)\)。
再令 \(x_2 = -0.60088\)，如此迭代下去。可以发现，\(x_n\) 会逐渐逼近零点。
刚才说切线方程为 \(y = f'(x_0)(x - x_0) + f(x_0)\)。如果令 \(y = 0\)，得到的 \(x\) 便是切线方程与 \(x\) 轴的交点，为
运用于多项式，假设要求使 \(f(g(x)) \equiv 0(\bmod \ x ^ n)\) 的多项式 \(g(x)\)，并且已经知道 \(f(g_0(x)) \equiv 0 (\bmod \ x ^ {\frac{n}{2}})\)。
那么可以说，
接下来解决多项式 Exp。所求为 \(g(x)\) 使得 \(g(x) \equiv e ^ {f(x)} (\bmod \ x ^ n)\)。两边都取 \(\ln\) 得到：
移项得：
设 \(F(g(x)) = ln g(x) - f(x)\)，那么所求就是 \(F(x)\) 的零点。
假设已经有 \(g_0(x)\) 使得 \(F(g_0(x)) \equiv 0 (\bmod \ x ^ {\frac{n}{2}})\)，根据上面的牛顿迭代，有：
根据这个柿子倍增求即可。每次需要计算一个 \(\ln\)，一个乘法，时间 \(O(n \log n)\)。
写的有点丑，超级大肠数。
void Exp(int *f, int *g, int n) {
if (n == 1) return void(g[0] = 1);
Exp(f, g, (n + 1) >> 1);
int B = (n << 2) + 5; int *lnb = new int[B]();
rop(i, 0, n) lnb[i] = g[i]; Ln(lnb, n);
tmp = new int[B](); rop(i, 0, n) tmp[i] = f[i];
rop(i, 0, n) tmp[i] = (1ll * tmp[i] - lnb[i] + p) % p;
tmp[0] ++ ; NTT(g, n, tmp, n);
free(tmp); tmp = NULL; free(lnb); lnb = NULL;
}
多项式快速幂（PolyPower）
在模 \(x ^ n\) 意义下计算 \(f^k(x)\)。
有了前面的知识铺垫，这部分就非常的简单。
根据对数恒等式，有 \(f(x) = e ^ {\ln f(x)}\)。
因此 \(f^k(x) = e ^ {k \ln f(x)}\)。
把 \(f(x)\) 乘以 \(k\)，求多项式 \(\ln\)，然后再 \(\exp\) 回来就行了。
void Power(int *f, int n, int k) {
Ln(f, n); rop(i, 0, n) f[i] = 1ll * f[i] * k % p; Exp(f, n);
}
多项式开根
在模 \(x ^ n\) 意义下计算 \(f^{\frac{1}{k}}(x)\)。
这个最简单。直接把 \(\frac{1}{k} \bmod p\)，然后多项式快速幂。
生成函数
定义
定义形如 \(f(x) = \sum \limits_{i = 0}^{\infty} a_i x ^ i\) 的式子为生成函数，其中 \(x\) 是一个不定元，取值需要保证 \(f(x)\) 收敛。需要注意的是，\(x\) 在生成函数中并不以未知数的形式单独出现，其意义也脱离了代数上的未知数本身。
生成函数大致分为两种：\(\text{OGF}\) 和 \(\mathrm{EGF}\)。前者主要用于无标号问题的计数，后者主要应用于有标号问题的计数。
为了书写方便，在下文中，将 \(a_0 + a_1 x + a_2 x ^ 2 \cdots\) 简写成 \(\{a_0, a_1, a_2 \cdots\}\)。
约定
-
为了书写方便，在下文中，将 \(a_0 + a_1 x + a_2 x ^ 2 \cdots\) 简写成 \(\{a_0, a_1, a_2 \cdots\}\)。
-
将 \(f(x)\) 中 \(x ^ i\) 的系数记为 \([x ^ i]f(x)\)，简记为 \(f(x)[i]\)。
数学基础
- \(\mathrm{D}\) 算子（求导算子）
\(\mathrm{D} f(x) = \lim \limits_{\delta \rightarrow 0} \dfrac{f(x +\delta) - f(x)}{\delta}\)。
对于 \(f(x)[i]\)，对其施加以求导算子之后，\((\mathrm{D}f(x))[i] = (i + 1)f(x)[i + 1]\)。
- 上升幂和下降幂
定义 \(x ^ {\underline{m}}\) 为 \(x\) 的 \(m\) 次下降幂，\(x ^ {\underline{m}} = x(x - 1)(x - 2) \cdots (x - m + 1)\)。
定义 \(x ^ {\overline m}\) 为 \(x\) 的 \(m\) 次上升幂，\(x ^ {\overline m} = x(x + 1)(x + 2) \cdots (x + m - 1)\)。
下面是关于上升 / 下降幂的有用的性质：
-
\(x ^ {\underline{m + n}} = x ^ {\underline{m}} (x - m) ^ {\underline{n}}\)
-
\(x ^ {\overline{m + n}} = x ^ {\overline{m}} (x + m) ^ {\overline{n}}\)
-
$x ^ {\underline{m}} = (-1)^ m (-x) ^ {\overline{m}} $
-
$x ^ {\overline{m}} = (-1)^ m (-x) ^ {\underline{m}} $
-
\(\Delta\) 算子（差分算子）
类似求导算子，我们定义差分算子 \(\Delta\)，\(\Delta f(x) = f(x +1) - f(x)\)。
它不具有求导算子那样优美的性质，但是其对于下降幂来说，与求导的运算法则相同。具体的，\(\Delta (x ^ {\underline{m}}) = m x ^ {\underline{m - 1}}\)。
可以发现，差分算子和求导算子十分相似，他们也有一些比较相似的性质，例如：\(\mathrm{D}(e ^ x) = e ^ x, \Delta(2 ^ x) = 2 ^ x\)。
后面的两个公式常用于上升幂和下降幂的转化。
生成函数的封闭形式
对于 \(\mathrm{OGF}\)，其常常有自己的封闭形式。下面举几个例子。
- Example 4.1： \(\{1, 1, 1,1 \cdots\}\) 的生成函数。
这是 OIer 最喜闻乐见的式子。不妨设 \(f(x) = \sum \limits_{0}^{\infty} x ^ i\)，则有 \(xf(x) = \sum \limits_{1}^{\infty} x ^ i\)。可以发现，这相当于对 \(f\) 施加了 平移算子 \(\mathbf{E}\)。将两个错项相减可以得到：
我们称 \(\dfrac{1}{1 - x}\) 为 \(f(x)\) 的封闭形式。上面计算生成函数封闭形式的做法称为错位相减，是小学数学常用的一种方法。
利用上面的算法，可以求出下面几个生成函数的封闭形式：
-
\(\{1, 1, 1, 1 \cdots\} \stackrel{\text{OGF}}{\longrightarrow} \dfrac{1}{1 - x}\)
-
\(\{1, a, a^2, a^3 \cdots\} \stackrel{\text{OGF}}{\longrightarrow} \dfrac{1}{1 - ax}\)
-
\(\{1, x^{k}, x^{2k}, x^{3k} \cdots\} \stackrel{\text{OGF}}{\longrightarrow} \dfrac{1}{1 - x ^ k}\)
-
\(\{1, c^1x^k, c^2x^{2k} \cdots\} \stackrel{\text{OGF}}{\longrightarrow} \dfrac{1}{1 - cx^k}\)
-
\(\{0, 1, \frac{1}{2}, \frac{1}{3} \cdots\} \stackrel{\text{OGF}}{\longrightarrow} -\ln(1 - x)\)
-
\(\{1, 1, \frac{1}{2!}, \frac{1}{3!} \cdots\} \stackrel{\text{OGF}}{\longrightarrow} e^x\)
-
\(\{1, 1, 1 \cdots\} \stackrel{\text{OGF}}{\longrightarrow} \dfrac{1}{1 - x}\)
封闭形式的展开技巧
- 泰勒展开 / 麦克劳林展开
上面的式子称为麦克劳林展开。注意，上面的式子没有考虑到 \(f\) 的敛散性。
通过麦克劳林展开，我们可以得到几乎所有函数的展开式。
- 换元法
利用上面得到的重要结论
将其中的 \(x\) 换成 \(qx\)，可以得到：
可以使用还原得到一些其他结论。
Example 5.1 求 \(f(x) = \dfrac{3}{1 - 4x}\) 的展开形式。
Example 5.2 求 \(f(x) = \dfrac{1}{1 + x}\) 的展开式。
Example 5.3 求 \(f(x) = \dfrac{5}{3 - 4x}\) 的展开式。
可以发现，这个方法非常好用。它可以展开几乎一切分母为一次的分式。
- 裂项法
上面的换元法非常好用，但是只适用于 \(-1\) 次的式子。对于高次的式子，我们尝试将他变成 \(-1\) 次的进行解决。
Example 5.4 求 \(f(x) = \dfrac{1}{x ^ 2 - 4x +3}\) 的展开式。
考虑到分母可以表示成 \((1 - x)(3 - x)\) 的形式，我们尝试裂项。
不妨设 \(f(x) = \dfrac{1}{(1 - x)(3 - x)} = \dfrac{\mathcal{A}}{1 - x} +\dfrac{\mathcal{B}}{3 - x}\) 的形式。
可以发现，\(\dfrac{\mathcal{A}}{1 - x} +\dfrac{\mathcal{B}}{3 - x} = \dfrac{\mathcal{A}(3 - x) +\mathcal{B} (1- x)}{(1 - x)(3 - x)}\)
于是有 \(\mathcal{A}(3 - x) +\mathcal{B} (1- x) = 1\)。解这个方程，得到：
对于分母更高次的情况，只要有实根，就可以裂项降次。
- 递推法
这个方法用于补裂项法的坑。
有的时候，分母是高次方程且没有实根，这非常不好，因为没法裂项。这时候可以使用这个方法。
Example 5.5 求 \(f(x) = \dfrac{1}{1 - 2x + 7x ^ 2}\) 的展开形式。
我们发现对于分母，\(\Delta = 4 - 28 < 0\)，因此没有实根，无法裂项。
考虑设 \(f(x) = \dfrac{1}{1 - 2x + 7x ^ 2} = a_0 + a_1x + a_2 x ^ 2 \cdots\)
则有
做一下这个卷积，可以得到
因此，\(a_0 = 1, a_1 = 2\)，对于 \(n > 1\)，\(a_n = 2a_{n - 1} - 7 a_{n - 2}\)。这样我们得到一个递推形式。
利用特征根方程即可求出该递推式的通项。
学了上面这么多展开技巧，我们来举几个实际例子。
Example 5.6 斐波那契数列通项
定义 \(f_0 = 0, f_1 = 1\)，\(\forall n \ge 2, f_n = f_{n - 1} + f_{n - 2}\)。求 \(f\) 的通项。
不妨设 \(\mathcal{F}(x) = \sum f_i x_i = \{0, 1, 1, 2, 3, 5, 8 \cdots\}\)
我们对 \(F\) 施加一个平移算子，也就是乘上 \(x\)，得到
再施加一次平移算子，得到
可以发现，\((\mathcal{F}(x) - x\mathcal{F}(x) - x ^ 2 \mathcal{F}(x))[n] = 0\)（As for \(x \ge 2\)）。对于 \(x < 2\)，我们强行补上即可。所以得到：
这样我们得到了 \(\mathcal{F}(x)\) 的封闭形式。
接下来我们要对这个封闭形式进行展开。发现分母有实根，这非常好。我们求出它的两个实根，分别为
采用展开技巧中的裂项法对他进行裂项，得到
可以解得 \(\mathcal{A} = \dfrac{\sqrt5}{5}, \mathcal{B} = -\dfrac{\sqrt5}{5}\)。
将 \(\mathcal{A, B}\) 代入并进行一顿化简（化简过程使用换元法）后，可以得到斐波那契数列的通项公式：
普通型生成函数的应用
Example 6.1 \(\texttt{ACW 3132}\)
一共八种物品，你要买这些物品。每个物品可以买无限件。
不妨将这八种物品设为 \(\mathcal{A, B, C, D, E, F, G, H}\)，每种物品的购买有限制：
-
\(\mathcal{A}\)：只能购买偶数个。
-
\(\mathcal{B}\)：只能购买 \(0\) 个或 \(1\) 个。
-
\(\mathcal{C}\)：只能购买 \(0\) 个，\(1\) 个或 \(2\) 个。
-
\(\mathcal{D}\)：只能购买奇数个。
-
\(\mathcal{E}\)：只能购买 \(4\) 的倍数个。
-
\(\mathcal{F}\)：只能购买 \(0, 1, 2\) 或 \(3\) 个。
-
\(\mathcal{G}\)：只能购买 \(\le 1\) 个。
-
\(\mathcal{H}\)：只能购买 \(3\) 的倍数个。
求购买 \(n\) 个物品的方案数。\(n \le 10 ^ {500}\)，答案对 \(10007\) 取模。
做法一：背包。设 \(f_i\) 表示选择了 \(i\) 个物品的方案数。转移即可。
做法二：流氓算法。使用背包打表，用 BM 弄出通项。
做法三：使用生成函数。
我们考虑每种物品的生成函数对应的是什么。对于 \(\mathcal{A}\) 物品，不妨将其生成函数设为 \(\mathcal{A(x)}\)，后面同理。
-
\(\mathcal{A(x)} = 1 + x ^ 2 +x ^ 4 +\cdots = \dfrac{1}{1 - x ^ 2}\)
-
\(\mathcal{B(x)} = 1 + x = \dfrac{1 - x ^ 2}{1 - x}\)
-
\(\mathcal{C(x)} = 1 + x + x ^ 2 = \dfrac{1 - x ^ 3}{1 - x}\)
-
\(\mathcal{D(x)} = x + x ^ 3 + x ^ 5 + \cdots = \dfrac{x}{1 - x ^ 2}\)
-
\(\mathcal{E(x)} = 1 + x^4 + x^8 + \cdots = \dfrac{1}{1 - x ^ 4}\)
-
\(\mathcal{F(x)} = 1 + x + x ^ 2 + x ^ 3 = \dfrac{1 - x ^ 4}{1 - x}\)
-
\(\mathcal{G(x)} = 1 +x = \dfrac{1 - x ^ 2}{1 - x}\)
-
\(\mathcal{H(x)} = 1 + x ^ 3 + x ^ 6 +\cdots = \dfrac{1}{1 - x^3}\)
把这些东西乘起来消消乐，剩下的答案就是：
这样我们得到了封闭形式。展开就可以得到答案。我们尝试对这个东西进行展开。利用广义二项式定理，我们可以得到：
乘上 \(x\) 相当于对其施以平移算子，答案即为
Bonus：最后对于 \(\dfrac{1}{(1 - x) ^ 4}\) 的化简，其实有更简单的方法。
对于 \(\dfrac{1}{1 - x}\) 求三阶导，发现就等于 \(\dfrac{1}{(1 - x) ^ 4}\)。
Example 6.2 P2000 拯救世界
和上一题差不多，列出来十个生成函数，乘起来消消乐就可以了。
Example 6.3 Super Poker II
写出四种扑克的 \(\mathrm{OGF}\)，乘起来就可以了。由于没有绑账号所以没有写。
Some Important Tricks
- 对 \(\mathcal{F(x)}\) 乘以 \(\mathcal{A(x)} = 1 +x +x ^ 2 + x ^ 3 \cdots\)，可以求出 \(\mathcal{F(x)}\) 的前缀和。例子：差分与前缀和
指数型生成函数
指数型生成函数（\(\mathbf{EGF}\)），通常用于有标号方案计数，如图计数等。
对于数列 \(P\)，其 \(\mathbf{EGF}\) 定义为：
下面是一些常见数列的 \(\mathbf{EGF}\)。
-
\(\{1, 1, 1, 1 \cdots\} \stackrel{\text{EGF}}{\longrightarrow} e ^ x\)
-
\(\{1, -1, 1, -1 \cdots\} \stackrel{\text{EGF}}{\longrightarrow} e ^ {-x}\)
-
\(\{1, c, c^2, c^3 \cdots\} \stackrel{\text{EGF}}{\longrightarrow} e ^ {cx}\)
-
\(\{1, 0, 1, 0 \cdots\} \stackrel{\text{EGF}}{\longrightarrow} \dfrac{e^x + e ^ {-x}}{2}\)
-
\(\{1, a, a ^ {2 \over}, a ^ {3 \over}, a ^ {4 \over} \cdots \} \stackrel{\text{EGF}}{\longrightarrow} (1 + x) ^ a\)
上述推导可以直接在 \(0\) 处泰勒展开。
指数型生成函数应用
- 图计数
Example 8.1
\(n\) 个点的无向连通图计数。
设 \(B = \sum 2 ^ {\binom{i}{2}} x ^ i\)，表示无向图的方案数。
设 \(A = \sum f_ix^i\)，表示无向连通图方案数。
则有 \(B = e ^ A\)，将 \(B\) 取 \(\ln\) 可以得到 \(A\)。
